“流速大压强小”中的流速是相对地面的速度吗?
——对香蕉球现象的再分析
2021-05-15任少铎
任少铎
(厦门市海沧区东孚中学,福建 厦门 361000)
伯努利原理是初中物理的知识,教材并未给出其适用条件和具体公式形式,只是通过典型的定性实验阐释简单的规律:流体在流速大的地方压强小,流速小的地方压强大.[1]但课本并未强调所谓的“流速”应当是空气相对于地面的流速还是相对于被压物体的流速,根据课本之前的定义,如果没有特别说明参照物,参照物通常选地面.然而,又有人提出所谓的“流速”究竟是空气相对于被压物体的流速,否则在行驶的火车里做流速与压强的实验就很可能会出现与地面截然不同的效果.然而,根据这种理论,香蕉球现象就无法解释了!那么事实究竟如何呢?为了消除疑问,笔者查阅了相关资料,对伯努利原理进行了深度研究,并从科学严谨的角度,对香蕉球现象进行了再分析,以供广大师生参考.
1 问题的提出
在球类运动中,经常会见到球在飞行时偏离预定直线“拐弯”的现象,因为其轨迹类似香蕉的形状,于是称之为香蕉球,足球中又称为弧线球.香蕉球的原理并不复杂,根据初中阶段的“流速大压强小”的知识便可解释.如图1所示,球从右向左前进,并做顺时针旋转(从读者观察的角度),此时因为球对空气有“拖拽”效应,球的上方被球“拖拽”的气流就是“顺风”的,球下方气流则是“逆风”的,因此球上方的气流速度比下方大,由“流体在流速大的地方压强小”可知,球会受到一个向上的压力差,这个压力差会导致球偏离预定轨道.这种现象也称为马格努斯效应.[2]
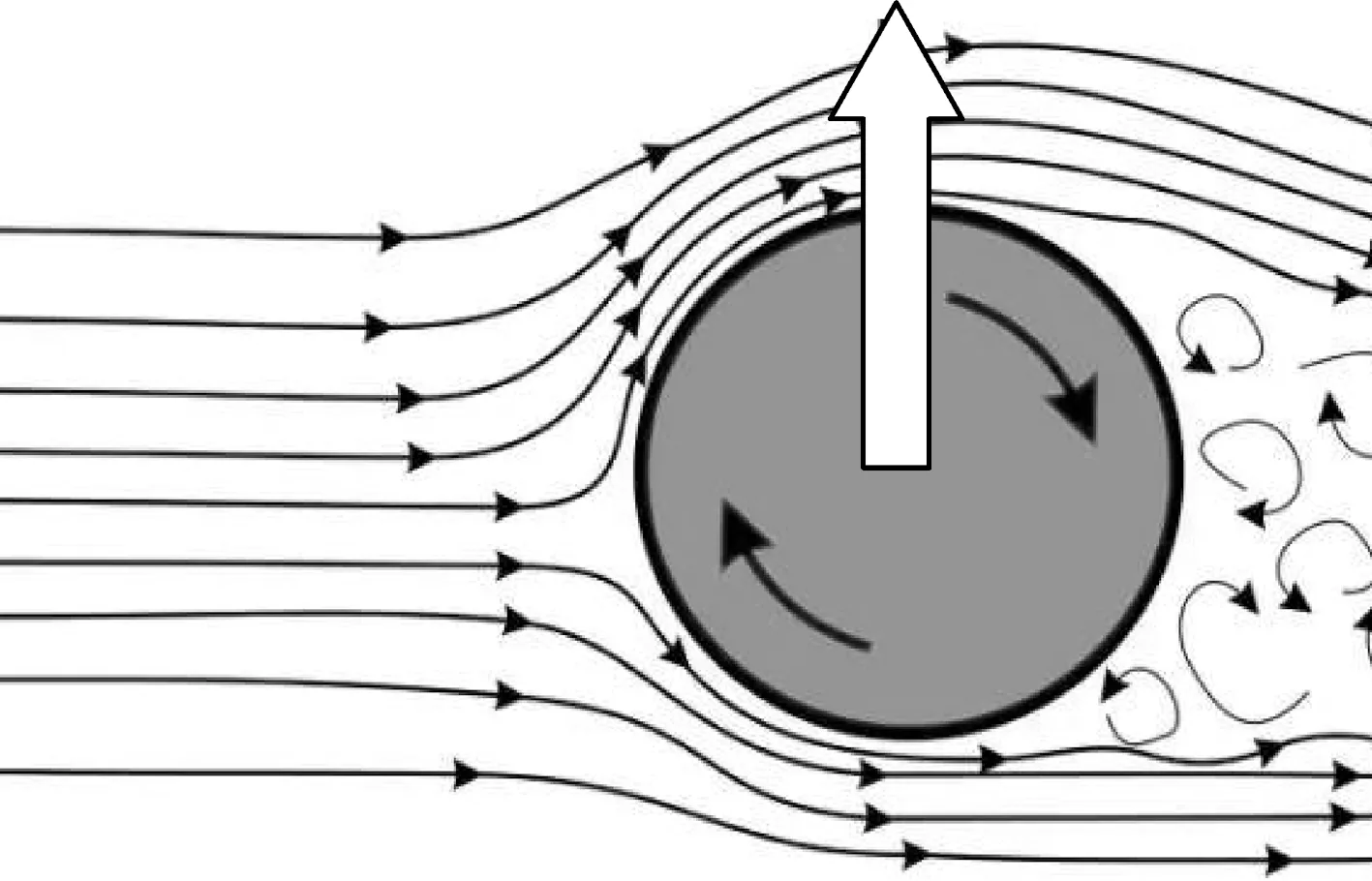
图1 经典的香蕉球现象原理图
这种解释与实际情况符合很好,一直以来广大中学师生也都是这么解释的.然而,在一次学术研讨时,一位同行却对此提出了不同看法.理由如下:“流速大压强小”中的流速应当是相对于“被压物体”的,流体对哪个物体产生压强,那么所谓的“流速”就应当是流体与这个物体的相对速度,而不是流体相对于地面的速度.例如:在高速行驶的车里(整个车里的空气也和车一起高速前进),做图2所示的实验,会发现乒乓球依然会向中间靠拢,但通过分析可得,此时两个乒乓球中间的气流速度反而比两边小(两边的气流和车一起高速前进),因此“流速大压强小”中的流速,不是流体相对于地面的速度,而应当是流体相对于“物体”的速度.

图2 在行驶的火车里对两个乒乓球中间吹气
但按照这个观点,香蕉球现象就无法解释了.图3中,虽然球的上方空气相对地面流速大,但球是顺时针旋转的,此时球的上表面有一个向右的旋转速度,空气相对于球上表面的流速并不一定比下表面大!假设球面旋转的速度为v1,来流的速度为v0,球面对空气的拖拽系统为u,那么

图3 空气相对于球面的流速分析
球上方的气流相对地面的速度为v上地=v0+uv1,相对于球面的速度为v上球=v0+uv1-v1;
球下方的气流相对于地面的速度为v下地=v0-uv1,相对于球面的速度为v下球=v0-uv1+v1.
通过化简可得,v上球=v0+(u-1)v1;v下球=v0+(1-u)v1.
由于球面对空气的拖拽系统为u与球面的粗糙程度和空气的温度等一系列因素有关,因此无法比较v0+(u-1)v1与v0+(1-u)v1的大小.更无法保证球上方的相对流速大于下方.
那么为香蕉球现象究竟该如何解释呢?这就需要对伯努利原理及其适用条件进入深入分析.
2 伯努利原理及其适用条件
“伯努利原理”由丹尼尔·伯努利(Nicolaus Bernoulli)在1726年提出.其推导过程如下.
假设理想流体在重力场中沿着一根流管作稳定流动,如图4所示,取管中的任意一段流体a1a2为研究对象,在经过一个非常短的时间Δt后,这段流体由a1a2流动到了b1b2;则有
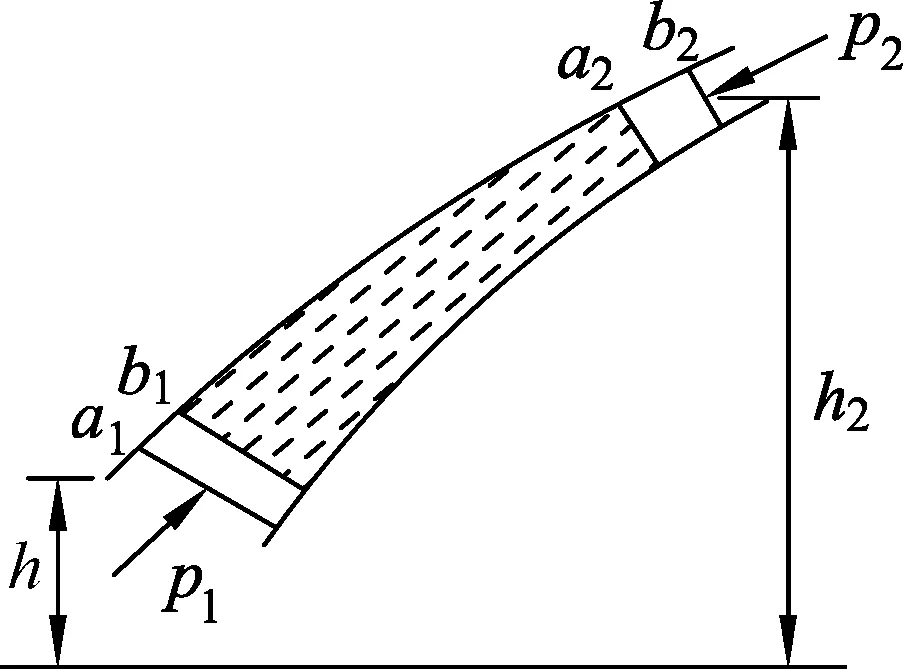
图4 伯努利方程的推导

两侧外力对所研究液体所做的功为W=W1+W2=(p1S1v1Δt-p2S2v2Δt)=(p1-p2)V
式中,m为这段液体的质量,v1、v2、p1、p2、S1、S2、h1、h2分别为液体在a1b1和a2b2处的流速、压强、截面积、高度.
根据功能原理,W=ΔE
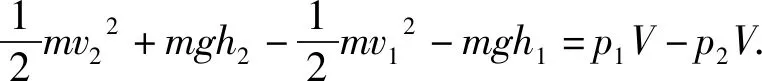
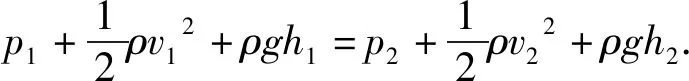
这就是伯努利方程,由于伯努利方程是由机械能守恒定律推导出的,因此其适用条件如下:
① 定常流(Steady flow):在流动系统中,流体在任何一点之性质不随时间改变.
② 不可压缩流(Incompressible fluid):流体的密度不随压力变化.
③ 无粘(Inviscous):摩擦效应可忽略,忽略黏滞性效应.
④ 同一条流线(Stream Line):流体元素沿着流线而流动,流线间彼此是不相交的;通俗的说,压力的比较必须在同一流线上才有意义(“前后”比较而不是“左右”比较).[3]
伯努利原理最为著名的推论为:流体在流速大的地方压强小.不难发现,这个描述并不严谨,其完整的表述应当为:对定常流动不可压缩的无粘流体,在同一条流线上,速度大的地方压强小.之所以强调“定常流动不可压缩的无粘流体”,是因为伯努利方程是由机械能守恒定律推导出的.
对于中学阶段而言,伯努利原理经常被“误用”,主要是因为对第④点没有深刻的认识,根据第④点,压力的比较必须在同一流线上才有意义,也就是说只有比较同一流线前后的压强才有意义.而我们通常是运用伯努利原理比较不同流线上的压强,这就导致了不少悖论.“流速大压强小”不可随意使用,只有对定常流动不可压缩的无粘流体,且在同一条流线上,才会有流速大的地方压强小.
可见,伯努利原理中的流速,既不是相对地面的,也不是相对于被压的物体的,而是相对于同一流线的,在同一流线上,流速大的地方压强小.之所以争论“流速大压强小”中流速相对谁的,是因为不清楚伯努利原理的本质及其适用条件.
3 香蕉球现象的再解释
图1中,球上方和下方的气流并不在同一流线上,显然不能直接比较两者的流速和压强.香蕉球现象的科学解释如下.

图5 正确运用伯努利原理分析香蕉球
不难发现,尽管气流1和气流2不在同一流线,但其初始状态(在无穷远处的状态)相同.因此我们可以通过与其初始状态相比来比较气流1和气流2的动压和静压大小.因此,香蕉球的原理仍然可以用伯努利原理解释,只是需要解释的更加严谨,而不是简单的“流速大压强小”.
笔者认为,在教学中,对香蕉球现象的讲解,可以采用以上观点以促进学生对现象的本质学习.在对伯努利原理深层理解的基础上,可通过图形图示等可视化手段原理图,直观揭示出上下两股气流的关系及其速度和压强变化情况,增加对香蕉球产生的原理感性认识,在形象思维与抽象思维间形成可视化的思维链条,[4]这样能较好地为科学推理扫平障碍,帮助个体顺利展开理性分析和逻辑推导,进而理解原理的深层内涵,把握问题的本质,有效地培养个体的科学思维能力,将核心素养落到实处.[5]
