鼓式制动器稳定性的复模态分析

2021-05-14王文竹张振伟程勉宏孙东锋

科学技术与工程 2021年10期

王文竹，李杰，刘刚，张振伟，程勉宏，孙东锋

(1.沈阳航空航天大学机电工程学院，沈阳 110136； 2.吉林大学汽车仿真与控制国家重点实验室，长春 130025； 3.锦西工业学校机械系，葫芦岛 125001)

制动噪声是汽车噪声、振动与声振粗糙度(noise,vibration,harshness,NVH)的重要组成部分，其具有频率高(高达16 kHz)，强度大(高达110 dB)，不仅会大大降低乘坐舒适度，还会造成严重的环境污染[1]。从20世纪30年代开始，研究者主要从实验、发生机理和数值仿真3个方面对制动噪声问题开展研究[2-3]。然而，制动噪声发生机理复杂，同时受制动器结构、制动工况和摩擦特性等因素的影响[4]，到目前为止对于抑制制动噪声还没有形成有效的控制手段[5-6]。

大量的文献对盘式制动器的制动噪声问题进行了研究，而对鼓式制动器的研究相对较少。鼓式制动器作为一种最基本形式的制动器，因其具有结构简单、成本低廉、性能可靠和方便安装驻车制动等优点，具有广泛的应用。相比较盘式制动器而言，摩擦面积大、散热差和制动力大，因此，鼓式制动器的制动噪声问题更为突出。

基于有限元法的复模态分析是当前对制动噪声预测分析的有效方法[7-8]。一些中外学者采用复模态分析方法对鼓式制动器的稳定性问题进行了研究。Huang等[9]采用数值模拟的方法对鼓式制动器进行了复模态分析，研究表明，在摩擦的作用下，当制动鼓和制动蹄的静态频率接近且振型满足一定条件时，会发生模态耦合而产生制动噪声，同时对摩擦衬片刚度和轮缸刚度等参数进行了灵敏度分析，讨论了摩擦系数对制动噪声影响。AbuBakar等[10]分别采用复特征值分析和瞬态分析两种方法对鼓式制动器制动稳定性进行了研究，对恒定摩擦系数和随相对速度负斜率变化的摩擦系数下的制动噪声进行了分析。庞明等[11]采用复模态分析对某鼓式制动器的制动噪声进行了预测，分别对摩擦系数、摩擦衬片杨氏模量、制动压力3个影响因素进行了分析。黄泽好等[12]建立了鼓式制动器的有限元模型，利用复模态分析方法对鼓式制动器的不稳定时变特性进行了研究，重点分析了弹性模量和膨胀系数对鼓式制动器不稳定性的影响。以上文献研究只分析了部分因素对鼓式制动器制动噪声的影响。为了抑制鼓式制动器的制动噪声，有必要对制动噪声的影响因素进行全面的分析。

针对某鼓式制动器出现的制动噪声问题，总结复模态分析的基本原理，在鼓式制动器有限元模型的基础上，应用复模态分析方法对制动稳定性进行预测。对影响制动噪声的不同参数进行全面分析。为抑制鼓式制动器的制动噪声提供理论基础。

1 复模态分析基本原理

1.1 动力学方程及其解

鼓式制动器接触摩擦的动力学方程为

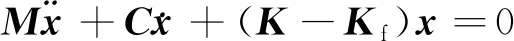
(1)

式(1)中：M、C、K分别为制动器的质量矩阵、阻尼矩阵和刚度矩阵；x为制动器的变形位移向量；Kf为摩擦刚度矩阵。

由于Kf为非对称刚度矩阵，对式(1)采用复模态分析方法进行求解。

设式(1)的解为

x=φeλt

(2)

式(2)中：φ为特征向量；λ为特征值。

将式(2)代入式(1)中，可得

(λ2M+λC+K-Kf)φ=0

(3)

对式(3)求解方程，求出复特征值和复特征向量，设第k阶特征值为

λk=σk±jωk

(4)

式(4)中：σk为第k阶特征值的实部；ωk为第k阶固有频率。

系统的第k阶运动可以由第k阶的复特征值和复特征向量来表示，即

xk=φke(σk+jωk)t+φke(σk-jωk)t=

φkeσkt(ejωkt+e-jωkt)

(5)

由于

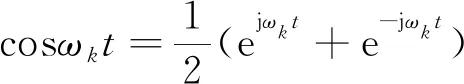
(6)

所以

xk=φkeσktcosωkt

(7)

1.2 不稳定系数

由式(7)可以看出，当特征值实部σk>0时，第k阶运动的振幅会随着时间t越来越大，系统会变得不稳定；相反，当特征值实部σk为负值时，第k阶运动的振幅会随着时间t越来越小，系统处于稳定状态。

鼓式制动系统的稳定性通常由系统的不稳定系数来衡量，第k阶不稳定系数定义为

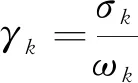
(8)

当γk>0时，即实部σk>0，系统将处于不稳定状态而发出制动噪声。在实际工程中，一般将不稳定系数0.01作为界限，即不稳定系数大于0.01为不稳定模态[13]。

2 鼓式制动器复模态分析

2.1 有限元模型的建立

2.1.1 有限元网格的划分

首先，根据有限元分析的具体任务，对鼓式制动器CATIA三维模型进行简化，最终的三维模型包括制动鼓、制动蹄、摩擦衬片和支撑板组成。其次，利用HyperMesh软件对鼓式制动器三维模型进行几何处理和网格划分，如图1所示。生成的有限元网格包括30 747个单元和48 122个节点，单元类型有两种，分别为C3D8I和C3D6。

2.1.2 材料属性的添加

添加各零件材料属性，如表1所示。

2.1.3 接触和绑定关系的建立

各零件之间的连接关系如表2所示。

图1 鼓式制动器有限元模型

表1 零部件的材料属性

2.1.4 约束和载荷的施加

鼓式制动器各零件的约束情况如表3所示。液压轮缸作用在制动蹄上的力简化为集中力，分别作用在领蹄和从蹄的相应节点上。

2.1.5 分析步的设置

共5个分析步，如表4所示。

表2 各零件的连接关系

表3 约束的施加

表4 分析步

2.2 鼓式制动器制动噪声的预测

图2 不稳定系数

应用ABAQUS软件对鼓式制动器进行复模态分析，得到(0～16)×103Hz频率范围内的不稳定系数，如图2所示。在693、14 486、15 357 Hz频率处,出现了不稳定系数大于0.01的情况，即为不稳定模态。其中，693 Hz频率处的不稳定系数为0.06，制动噪声的不稳定倾向最为明显。

图3 不稳定模态振型图

3个不稳定模态的振型如图3所示, 可以看出693 Hz的振型为整体一阶弯曲振动，其他两个模态振型为制动鼓和制动蹄的高阶弯曲局部振动。

3 影响因素分析

为了研究不同因素对鼓式制动器制动噪声的影响，采用不稳定倾向系数(TOI)对不同条件下进行整体评价，其定义为

(9)

TOI本质上是用系统的不稳定系数γk来评价制动噪声的倾向性。通过对某一工况下系统所有不稳定模态对应的不稳定系数求和得到，可对不同工况下的制动不稳定性进行对比分析。

3.1 制动压强的影响

为了说明制动压强对制动噪声的影响，液压轮缸的制动压强分别取0.5、1、1.5 MPa，其结果如图4所示。

制动压强对鼓式制动器的制动噪声具有较大的影响。制动压强和制动噪声之间的关系比较复杂，不是简单的线性关系。在0.5 MPa时，不稳定模态数为2个，不稳定倾向系数TOI=32，系统相对最为稳定。在1 MPa时，不稳定模态数为3个，不稳定倾向系数TOI=110，系统相对最不稳定。

3.2 制动鼓角速度的影响

制动鼓角速度ω分别取2.5、5、7.5 rad/s，结果如图5所示。

不同制动鼓旋转速度下的不稳定模态数和不稳定系数几乎相同。随着速度的增加，不稳定倾向系数保持不变。说明制动鼓旋转速度对制动噪声几乎没有影响。

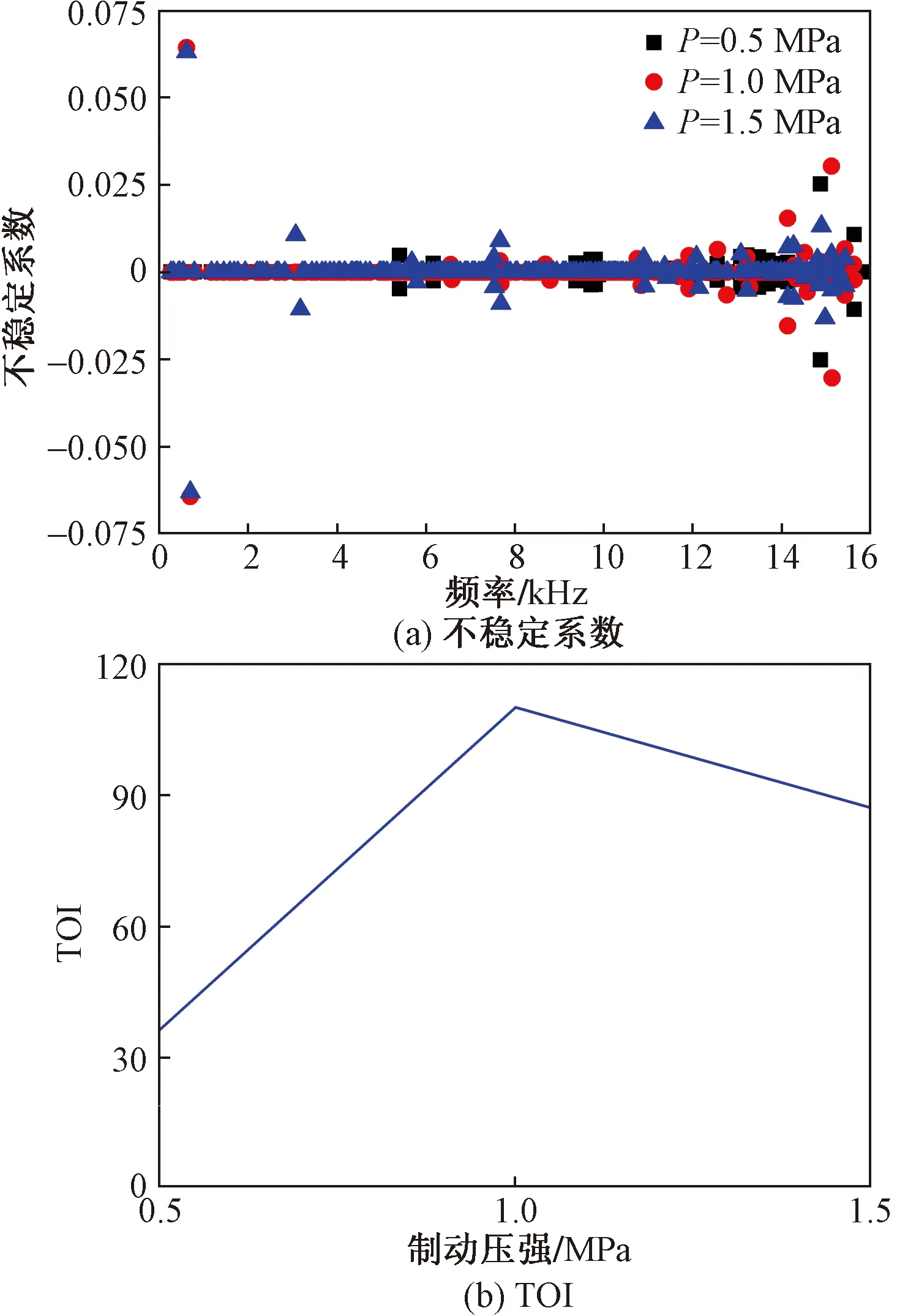
图4 制动压强的影响

图5 制动鼓转速的影响

3.3 摩擦系数的影响

摩擦系数f分别取0.3、0.35、0.4，结果如图6所示。

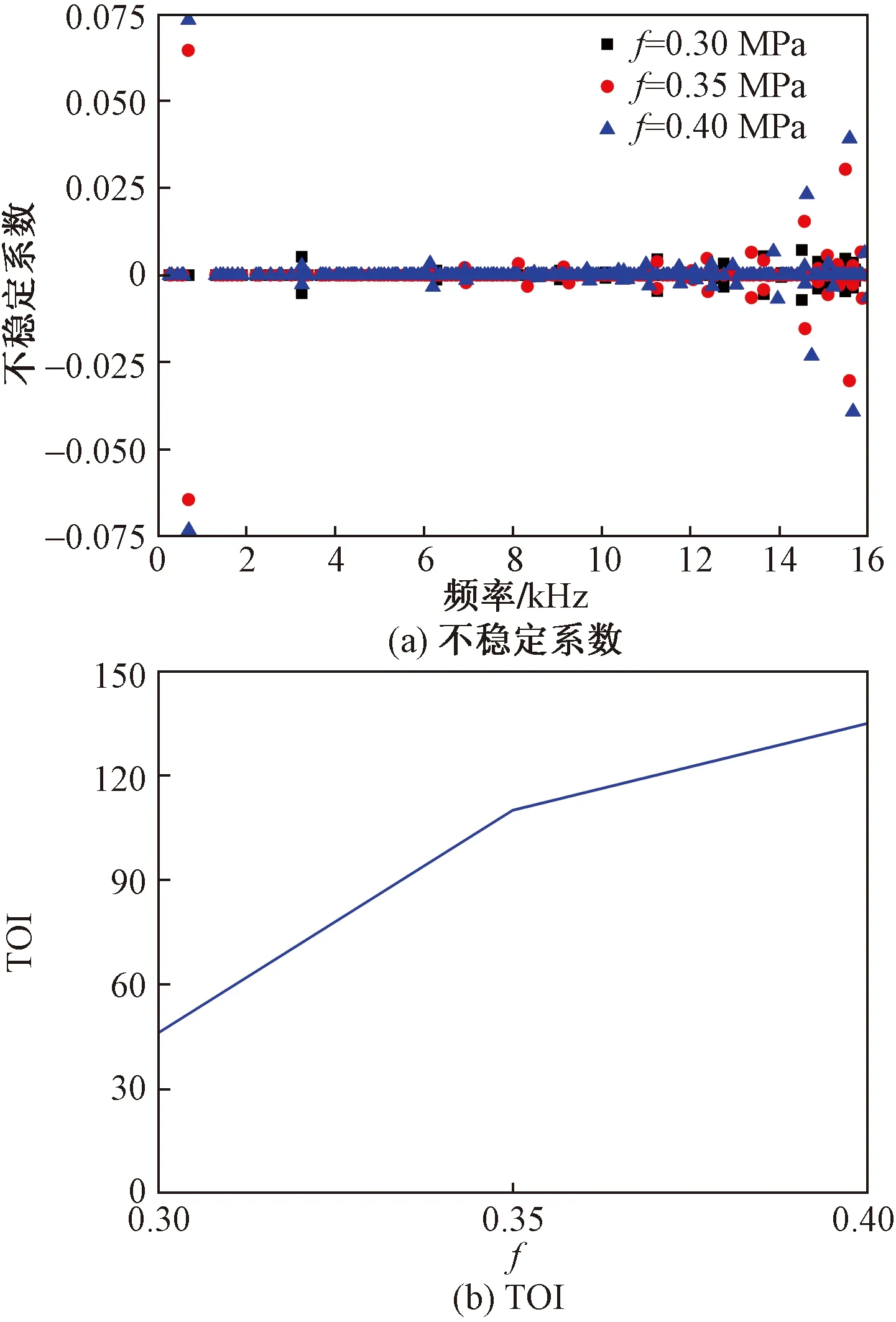
图6 摩擦系数的影响

摩擦系数对鼓式制动器的制动噪声具有较大影响。随着摩擦系数的降低，鼓式制动器的不稳定模态数减少，不稳定倾向系数明显降低，系统相对更加稳定。但摩擦系数与制动效能直接相关，减少摩擦系数会降低制动系统的制动性能。因此选择摩擦系数时，应该权衡制动噪声和制动性能。

3.4 杨氏模量的影响

为了研究零件材料杨氏模量对制动噪声的影响，分别分析摩擦衬片、制动蹄和制动鼓零件材料杨氏模量对制动噪声的影响。

摩擦衬片杨氏模量E1分别取1.55、3.10、4.65 GPa，结果如图7所示。

摩擦衬片杨氏模量对制动噪声影响很大。二者之间关系较为简单，摩擦衬片杨氏模量越大，不稳定倾向系数越小，系统相对越稳定。

图7 摩擦衬片杨氏模量的影响

制动蹄杨氏模量度E2分别取103.5、207.0、310.5 GPa，结果如图8所示。

图8 制动蹄杨氏模量的影响

制动蹄杨氏模量对鼓式制动器制动噪声具有一定影响。二者之间的关系比较简单，制动蹄的杨氏模量越大，不稳定倾向系数越小，系统相对越稳定。

制动鼓杨氏模量度E3分别取55、110、165 GPa，结果如图9所示。

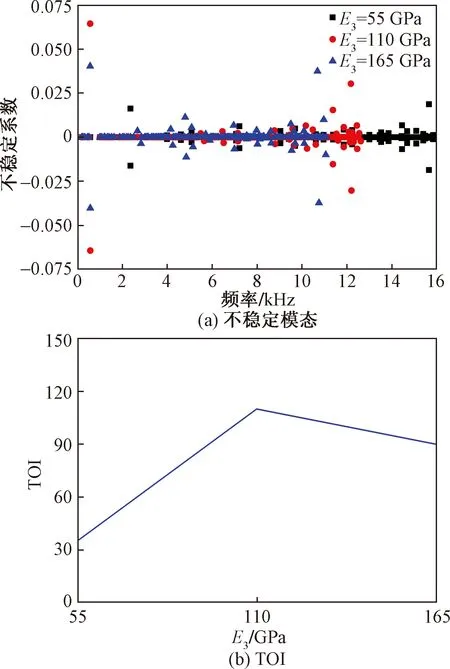
图9 制动鼓杨氏模量的影响

制动鼓杨氏模量对制动噪声具有较大影响。二者之间关系比较复杂，制动鼓的杨氏模量对制动噪声之间没有明显规律。在3种制动鼓杨氏模量中，当E3=55 GPa，不稳定模态(不稳定系数大于0.01的数量)数为2，不稳定倾向系数为35，鼓式制动器系统相对最为稳定。当E3=110 GPa时，不稳定模态数为3，不稳系统倾向系数为110，系统相对最不稳定。