1951—2017年松花江流域连续性极端降水事件时间趋势特征分析

蔡文香， 卢万合， 于国强， 刘家福

(1.吉林师范大学数学与统计学院， 四平 136000； 2.吉林师范大学旅游与地理科学学院， 四平 136000)

极端天气、气候事件简称极端气候事件，主要包括极端温度与极端降水两个方面。学术界普遍认为极端气候事件频次和强度的变化将深刻影响着人类社会和自然环境[1]。与偶发性极端气候事件相比，连续性极端气候事件对于自然系统及人类活动具有更大的影响[2]。因此，采用定量的方法对分析典型区域连续性极端气候事件的特征是管理和防范灾害风险的基础。

近年来，极端气候事件研究已经成为国际范围内的热点问题，研究内容主要为极端温度与极端降水的发生规律、成因及其影响[3]。该领域已经开展了大量的学术研究工作：雅茹等[4]基于内蒙古自治区气象日值数据,选取与水热组合、植被生长、农牧业发展息息相关的14个极端气候事件相关指数,利用线性趋势、M-K检验等方法,分析了内蒙古地区极端气候事件的时空变化规律；梁晓燕等[5]、蒋珊珊[6]、胡晓英等[7]采用前述方法分析了甘肃省、辽西地区、珠江流域极端气候事件的时间变化趋势和空间分布规律；程玉菲等[8]分析了疏勒河流域极端水文事件对极端气候事件的响应关系，结果表明该流域极端洪水事件主要受控于极端降水，极端枯水事件主要受控于极端低温；Lin等[9]以中国为例，研究了城市化对于极端降水事件的影响，结果表明城市化对沿海地区极端降水事件的影响趋于弱化，对中西部地区极端降水事件的影响趋于强化；Frame等[10]以新西兰为例，量化分析了人类对气候系统的干扰而造成的与极端天气有关的近期成本。目前极端气候事件虽然取得了大量的研究成果，但连续性极气候事件的研究成果还相对较少，主要是以国家为对象的宏观分析，文献[2，11]通过4项指标，分析了中国连续性极端温度与极端降水的发生规律，而且对于极端气候事件的时间趋势分析，主要采用线性回归的方法，样本数较少时准确性得不到保证。

松花江流域是中国七大流域之一，地处东北北部地区，流域内水文灾害严重。松花江流域的极端降水事件是极端水文事件发生的重要原因。学术界对松花江流域极端降水特征、趋势等问题的研究已经取得了一些成果[12-15]，但针对松花江流域极端降水事件时空特征的专门研究较少，隋佳硕[16]在分析松花江上游降水量的空间分布时，探讨了该区域极端降水量及其频数的变化。现基于1951—2017年的气象站点数据，采用泊淞回归的方法，探索松花江流域连续性极端降水事件时间趋势特征，以期为松花江流域的灾害防治、水资源管理提供有益参考。

1 研究区概况

松花江流域南北长1 070 km，东西920 km，介于41°42′～51°38′N，119°52′～132°31′E，流域面积约为54.6×104km2，占黑龙江流域总面积的29.4%,流域西部为大兴安岭，北部为小兴安岭，东部和东南部为完达山脉和长白山脉，中部为松嫩平原，是本流域的主要农业地区，西南部丘陵地带是松花江、辽河两流域的分水岭[5，17]。松花江流域多年平均年降雨约563 mm，东南部山区降水可达700～900 mm，干旱的流域西部地区仅400 mm，其中第二松花江、嫩江流域、松花江干流流域的多年平均降雨量分别为668.39、565.47、454.96 mm[18-19]。近年来，松花江流域的暴雨灾害频繁发生，造成了严重的损失，因此，松花江流域是中国防汛抗洪的重点区域[20]。

2 数据与方法

研究所用数据来自中国气象数据共享服务网,采用R软件进行预处理，剔除数据缺失站点，最终获得41个气象站(图1)1951—2017年逐日降水资料。极端降水阈值采用百分位法，将1951—2017年逐日降水数据按照升序排序，将第90、95、99百分位值对应的降水量定义为极端降水事件的阈值[21]。研究将连续性极端降水事件(CDEP)定义为某地连续2日以上发生日降雨量均大于该地极端降水事件阈值的事件，用连续性极端降水事件的发生天数作为研究指标。

以往相关研究中，学者通常采用线性回归的方法。然而，使用线性回归分析应首先满足线性条件，当观测数据是来自大样本的相对较少的计数时，假设就失效了。泊松分布回归通常将可能的结果限制在非负整数上，使其成为模拟罕见、离散事件发生的有效方法。研究采用泊松回归进行松花江流域连续性极端降水事件的变化特征分析，将任何降水事件j导致的连续性极端降水的天数记作Nj；一年中连续降水事件的次数为M，当M=0时，则表明没有发生极端降水事件；令Yi为第i年松花江流域CDEP的最大天数，其中i为1951—2017年中的任意一年，则有

图1 松花江流域气象站点分布

Yi=max{N1,N2,…,Nm}

(1)

CDEP是可数变量，Yi遵循泊松分布[22]，首先计算各个站点的CDEP，然后应用泊淞回归模型计算CDEP随时间变化的趋势特征，这里CDEP的发生概率为

(2)

式(2)中：

lnμi=α0+α1X

(3)

或

lnμi=β0+β1X+β2X2

(4)

式中：X为1951—2017年的时间序列;α0、α1为泊松对数线性回归模型(3)的回归系数；β0、β1、β2为泊松对数线性二次回归模型(4)的回归系数。以α1为例，在其他预测变量不变的情况下，年份每增加1年，CDEP的年最大天数对数均值相应增加α1。

3 结果分析

3.1 极端降水阈值特征

松花江流域地跨黑龙江省、吉林省和内蒙古自治区，包含三个子流域，降水量差异较大[23]。根据前述方法确定41个气象站的极端降水阈值，如表1所示。第90百分位阈值最小值为13.6 mm，最大值为17.97 mm，所有阈值对应的降水等级都是中雨，第95百分位阈值最小值为20.9 mm，最大值为 27.8 mm，对应的降水等级为中雨、大雨，其中阈值对应中雨的站点有28个，对应大雨的站点有13个，第99百分位阈值最小值为38.46 mm，最大值为54.975 mm，对应降雨等级为大雨、暴雨，其中对应大雨的站点有33个，对应暴雨的站点有8个。

3.2 流域时间趋势特征

运用R软件对41个站点数据进行统计分析，并将每年各站点连续性极端降水天数加总，得到1951—2017年松花江流域连续性极端降水的频次数据，再进行泊松回归分析，结果第90百分位阈值下、第99百分位阈值下连续性极端降水频次回归系数通过显著性检验，表明松花江流域在第90百分位阈值下、第99百分位阈值下连续性极端降水频次具有时间趋势特征(图2)。其中，第90百分位阈值下连续性极端降水频次的泊松一次回归系数为 0.006 818(显著性水平0.001)，指数化后的值为1.006 841，说明时间每增加1年，连续性极端降水频次将乘以1.006 841。第99百分位阈值下连续性极端降水频次的泊松一次回归系数为0.036 49(显著性水平0.01)，指数化后的值为1.037 159，说明时间每增加1年，连续性极端降水频次将乘以1.037 159。综合上述特征，可以看出松花江流域连续性极端降水呈现出快速增加的趋势，而且最为极端的连续性降水事件(第99百分位阈值)增加趋势尤为明显，流域内发生重大洪灾灾害的风险越来越大。

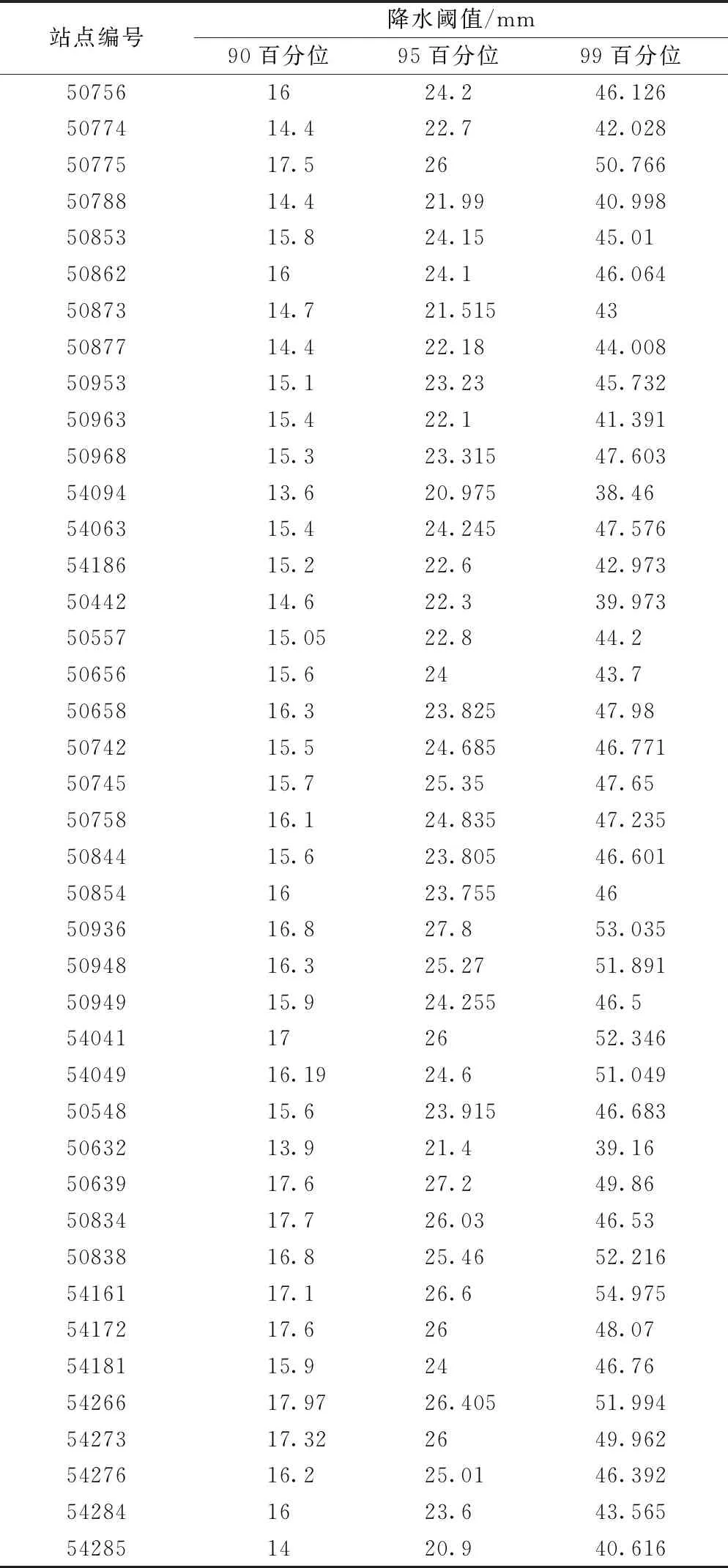
表1 各站点极端降水阈值

图2 松花江流域连续性极端降水事件拟合曲线

3.3 子流域时间趋势特征

运用前述方法，得到松花江干流流域、嫩江流域、第二松花江流域1951—2017年连续性极端降水的频次数据，进行泊松回归分析，各子流域在不同阈值下通过显著性检验(图3)。松花江干流流域在第99百分位阈值下连续性极端降水频次回归系数通过显著性检验，说明具有时间趋势性，泊松一次回归系数为0.049 68(显著性水平0.001)，指数化后的值为1.050 931，说明时间每增加1年，连续性极端降水频次将乘以1.050 931。嫩江流域在第90百分位阈值下、第95百分位阈值下连续性极端降水频次回归系数都通过显著性检验，表明嫩江流域第90百分位阈值下、第95百分位阈值下连续性极端降水频次具有时间趋势特征。其中，第90百分位阈值下的泊松一次回归系数为0.005 006(显著性水平0.01)，指数化后的值为1.005 018 623 3，说明时间每增加1年，连续性极端降水频次将乘以 1.005 018 623 3，第95百分位阈值下的泊松一次回归系数为0.005 824(显著性水平0.1)，指数化后的值为1.005 841 336 5，说明时间每增加1年，连续性极端降水频次将乘以1.005 841 336 5。第二松花江流域在第95百分位阈值下连续性极端降水频次回归系数都通过显著性检验，表明嫩江流域第95百分位阈值下连续性极端降水频次具有时间趋势特征，泊松一次回归系数为0.007 623(显著性水平0.05)，指数化后的值为1.007 653，说明时间每增加1年，连续性极端降水频次将乘以1.007 653。尽管各子流域在部分阈值下未能通过显著性检验，但综合已有结果，可以看出松花江各子流域连续性极端降水与流域总体特征一致，均呈现出不断增加的趋势，其中第90、95百分位阈值下的极端降水增长趋势相对平缓，第99百分位阈值下的增长趋势较为明显，说明发生洪涝灾害的风险越来越大。

3.4 各站点时间趋势特征

图3 松花江各子流域连续性极端降水事件拟合曲线

将时间序列进行标准化处理，对各站点连续性极端降水的频次数据进行泊松回归分析，在不同百分位阈值下均有站点通过显著性检验，汇总后如表2所示。第90百分位阈值通过显著性检验的站点共有9个， 6个站点(50658、50854、50862、50963、50948、50181)一次回归结果显著，其中50658、50854、50862站点一次回归为正值，说明这3个站点连续性极端降水频次呈现增加的趋势，50963、50948、50181一次回归系数为负数，说明这3个站点连续性极端降水频次呈现减少的趋势，1个站点(50656)二次回归结果显著，且二次回归二次项系数为正值，说明该站点连续性极端降水频次呈现先减少后增加的趋势，2个站点(50442、54049)一次回归、二次回归结果均显著，其中50442站点，一次回归系数为正值，二次回归二次项系数为负值，说明该站点连续性极端降水频次总体上呈现增加的趋势，具体表现为先增加，后减少的趋势，54049站点一次回归系数、二次回归二次项系数均为负值，说明该站点总体上呈现减少趋势，具体表现为先增加后减少的趋势。第95百分位阈值通过显著性检验的站点共有7个，4个站点(50774、50788、50862、50873)一次回归结果显著，其中50774、50788、50862站点一次回归系数为负值，说明这3个站点连续性极端降水频次呈现减少的趋势，50873站点一次回归系数为正值，说明该站点连续性极端降水频次呈现增加的趋势，2个站点(50442、54273)二次回归结果显著，50442站点二次回归二次项系数为负值，说明该站点连续性极端降水频次呈现先增加后减少的趋势，54273站点二次回归二次项系数为正值，说明该站点连续性极端降水频次呈现先减少后增加的趋势，1个站点(50758)一次回归、二次回归结果均显著，且一次回归系数、二次回归二次项系数均为正值，说明该站点连续性极端降水频次总体上呈现增加的趋势，具体趋势为先增加后减少。第99百分位阈值通过显著性检验的站点仅有1个(50873)，其一次回归系数为正值，说明该站点连续性极端降水频次呈现出增加的趋势。综合上述特征，可以看出松花江流域各站点极端降水的发生趋势呈现出显著的地域差异，既有上升，也有下降，而且部分站点通过了二次回归检验，发生趋势更为复杂，客观上也证明了泊淞回归在小尺度区域极端气候事件的研究中仍然有效。

表2 各站点泊淞回归结果

4 结论

(1)松花江流域连续性极端降水事件在第90百分位阈值、第99百分位阈值下通过泊淞一次回归的显著性检验，第90百分位阈值下指数化系数为1.006 841，第99百分位阈值下指数化系数为 1.037 159，呈现出增加的趋势，且后者的值远远大于前者，说明后者增加幅度更大，而第99百分位阈值下的连续性极端降水事件属于最极端的降水事件，该类事件的显著增加无疑会导致流域内洪涝灾害风险加大，相关部门需要加强警惕。

(2)松花江子流域连续性极端降水事件在不同百分位阈值下通过泊淞一次回归的显著性检验，均呈现出增加的趋势。松花江干流流域在第99百分位阈值下泊松一次回归指数化系数为1.050 931，说明该子流域最极端的降水事件增加幅度较大。嫩江流域在第90百分位阈值下、第95百分位阈值下通过检验，指数化系数分别为1.005 018 623 3、1.005 841 336 5，第二松花江流域在第95百分位阈值下通过检验，指数化系数为1.007 653。

(3)各站点流域连续性极端降水事件呈现显著差异，第90百分位阈值下9个站点通过检验，趋势特征为：4个站点增加，4个站点减少，1个站点先减少后增加，第95百分位阈值下7个站点通过检验，趋势特征为：2个站点增加，3个站点减少，1个站点先减少后增加，1个站点先增加后减少，第99百分位阈值下仅有1个站点通过检验，呈现增加的趋势。

5 讨论

目前，学术界有关极端降水事件趋势特征的研究成果很多[24-27]，尽管研究区域不同，但主要都是采用线性回归的方式。然而，使用线性回归分析应首先满足线性条件，当观测数据是来自大样本的相对较少的计数时，假设就失效了。本文研究对象为连续性极端强降水事件，相对于极端降水事件更为极端，也是流域内发生洪涝灾害的直接诱因，样本量相对较少，不适宜运用线性回归的方法，于是采用了泊松分布回归，其他领域的研究已经表明泊松回归是模拟罕见、离散事件发生的有效方法。已有研究成果[4]表明，泊松回归在研究国家、省级空间尺度上分析连续性极端降水事件上是可行的，本研究将该类研究的空间尺度扩展到流域、子流域和气象站点，结果表明仍然有效，研究结论可以为国家防灾减灾决策提供参考和依据。

基于松花江流域、松花江子流域的研究结果表明连续性极端强降水事件呈现增加的趋势，而在站点尺度上，仅有部分站点通过检验，呈现出差异性的趋势特征。后续研究重点可以从两个方面展开：一是在泊松回归基础上，继续探讨其他方法，尤其是站点尺度上的有效分析方法；二是进行连续性极端强降水与流域洪涝灾害的关联分析，构建不同空间尺度上的洪涝灾害预警预报体系。