基于IRS 辅助的SWIPT 物联网系统安全波束成形设计

朱政宇，徐金雷，孙钢灿,2,4，王宁，郝万明,4

（1.郑州大学河南先进技术研究院，河南 郑州 450001；2.郑州大学信息工程学院，河南 郑州 450001；3.郑州大学河南省智能网络和数据分析国际联合实验室，河南 郑州 450001；4.郑州大学产业技术研究院，河南 郑州 450001）

1 引言

6G 技术的进一步研究和发展，可以满足未来泛在物联网（IoT,Internet of things）的需求，但6G &IoT 的体系结构存在设备之间的资源分配、可持续通信、信息安全等一系列问题[1]。随着信息传输速率和移动终端数量迅速增加，信息传输的安全性和可靠性尤其重要。

大规模IoT 的应用发展极大地增加了无线设备的功耗，文献[2]设计了一种6G 蜂窝IoT 的大规模接入方案，以促进在有限频谱资源内实现高效的大规模接入，提高能量效率。针对接入IoT 设备高级别安全保护产生的高能耗问题，文献[3]提出一种基于人工智能的自适应安全规范方法，该方法能匹配相应业务需求，避免能量耗尽，提高工作时间。然而，如何为海量IoT 设备提供可持续的能量供应仍是一个巨大的挑战。对IoT 设备进行有线供电不适合大规模部署，而电池供电方式的储能能力有限，限制了整个IoT 的可持续运转[4]。更换电池可以解决网络中设备能源短缺的问题，但受大规模IoT 设备部署的环境制约，其成本高昂[5]。

近年来，作为IoT 设备供电的可靠方案之一，无线功率传输（WPT,wireless power transfer）技术自提出以来就受到学术界和工业界的广泛关注。文献[6]给出了集成能量、计算和通信的6G 蜂窝IoT理论框架，探讨使用WPT 对海量IoT 设备持续性供电的可能性，提出了一种收发双方的联合波束成形设计方案。文献[7]提出了一种谐振束充电方法，能实现远程WPT。无线携能通信（SWIPT,simultaneous wireless information and power transfer）[8-10]作为WPT 技术的应用之一，也是一种射频能量采集技术，即无线信息与能量同时传输。与WPT 不同之处在于，SWIPT 的无线设备进行能量交互的同时传输信息。文献[8]研究了一个具有全双工IoT 节点的SWIPT 系统，提出联合混合预编码器、译码规则和功率分配的优化方案，实现总传输功率最小化。因此，基于无线信号包含信息与能量这一特性，SWIPT 技术能够同时实现无线IoT 中设备的持续性供能和有效通信，符合新一代IoT 绿色通信的基本要求[9]。

另一方面，新兴的智能反射面（IRS,intelligent reflecting surface）[10-13]技术被认为是6G 系统的前景技术之一。IRS 是由大量低成本、亚波长结构和独立可控的无源电磁反射元件集成的均匀阵列平面[10-11]，其主要功能是根据信号传播反馈的通信链路信息，通过软件编程的方式调整反射信号的幅度和相位，使反射信号与其他路径的信号构造性相加，从而增强接收端期望信号功率，提高通信质量[12-13]。文献[14]针对IRS 辅助多用户SWIPT 系统最小采集能量的最大化问题，通过联合优化发射波束成形以及IRS 反射相移，提出一种基于最大最小准则的波束成形设计方法。文献[15]考虑一个IRS 辅助的多输入单输出（MISO,multiple input single output）SWIPT 系统，提出一种交替迭代和半定松驰（SDR,semidefinite relaxation）算法优化发射/反射波束成形，最大化能量采集器（EHR,energy harvesting receiver）加权和功率。

基于IRS 的主被动互惠传输技术是6G&IoT 系统物理层解决方案之一，同时也带来了新的物理层安全（PLS,physical layer security）[16-17]问题。文献[18]在IRS 辅助的高斯多输入多输出（MIMO,multiple input multiple output）系统窃听信道状态信息（CSI,channel state information）未知情况下，提出了一种联合barrier法和逐项优化法的交替迭代方法提高保密速率。文献[19]针对IRS 辅助的多天线保密传输系统中的发射功率最小化问题，提出了一种基于SDR 的交替迭代算法，并推导出安全波束成形的闭式表达式，提高功率分配方案的有效性。文献[20]针对IRS 辅助的SWIPT 系统中的能效最大化问题，在非线性能量采集模型下，通过采用人工噪声（AN,artificial noise）辅助形式，提出一种交替迭代法获得次优解。考虑窃听者的CSI 未知和不存在视距通信链路的情况，针对分布式IRS 辅助的多用户MIMO 传输系统的保密和速率最大化问题，文献[21]采用罚函数法、连续凸近似（SCA,successive convex approximation）和SDR 的联合优化策略，提出了一种稳健波束成形和AN 联合设计方案。然而上述文献中，文献[14-15]只考虑了IRS 辅助的SWIPT 系统模型，文献[18-21]的工作主要集中在研究传统的保密传输系统，而可有效提高保密速率和能量传输的干扰机技术[22-23]尚未得到研究。基于IRS 辅助的SWIPT通信系统通过利用外部干扰机发射干扰信号来对抗窃听，提高通信安全性，同时增强系统能量采集能力。

针对以上所述能量传输和信息安全问题，考虑基于干扰机和IRS 辅助SWIPT IoT 系统的PLS 问题具有重要理论意义和现实价值。本文具体研究工作如下。

1) 建立了一个基于干扰机和IRS 同时辅助的SWIPT IoT 系统保密通信链路。同时满足保密速率、发射功率和IRS 反射相移约束条件下，通过联合优化基站发射波束成形矩阵、干扰机协方差矩阵和IRS 相移，给出了EHR 模型。该问题是一个二次型约束的非凸二次型规划问题，难以直接求解。

2) 针对上述非凸二次型规划问题，提出了一种交替迭代优化算法。首先，针对非凸的保密约束条件，采用序列参数凸逼近（SPCA,sequential parametric convex approximation）将其转换为凸约束条件；然后，通过一阶泰勒展开、松弛变量、半定松弛法和辅助变量，将原非凸目标函数转化为凸近似形式；最后，提出基于SDR 的交替迭代算法求得原非凸问题的可行解。

3) 仿真结果验证了所提算法的收敛性，证明了基于IRS辅助的SWIPT IoT系统可以显著提升EHR的能量采集性能。与传统方案相比，使用IRS 在提高系统安全性和能量采集方面有很大优势。

2 系统模型

基于IRS 辅助的SWIPT IoT 系统模型如图1 所示，包括一个多天线基站、一个单天线合法IoT 设备和一个窃听设备Eve。假设Eve 比IoT 设备更靠近基站，则其具备窃听节点外信息的便利条件。在考虑信息安全传输时，将Eve 作为潜在的窃听设备是合理的。在传输的过程中，在IRS 附近部署一个EHR 来采集射频信号的能量。为提高信息传输的安全性，采用一台干扰机来发射干扰信号[22]。假设基站和干扰机均配置M根天线，IRS 配置N个反射单元。该系统考虑从基站到接收设备的典型下行链路传输，假设通过基于接收信号强度（RSS,received signal strength）、到达角度（AoA,angle of arrival）、到达时间（ToA,time of arrival）和到达时间差（TDoA,time difference of arrival）来获取Eve 的位置[24-26]。

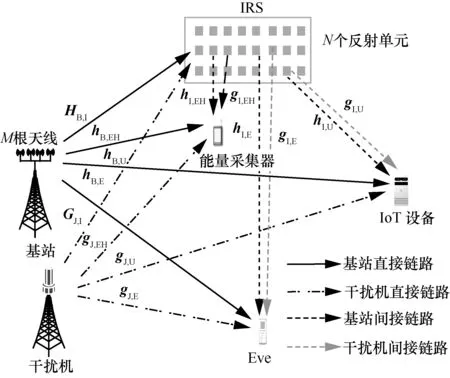
图1 基于IRS 辅助的SWIPT IoT 系统模型

为了实现SWIPT 系统在MIMO 窃听信道下的安全传输，假设基站到IRS、IoT 设备、EHR 和Eve的信道增益分别为HB,I∈CM×N、hB,U∈C1×N、hB,EH∈C1×N和hB,E∈C1×N，干扰机到IRS、IoT 设备、EHR 和 Eve 的信道增益分别为GJ,I∈CM×N、gJ,U∈C1×N、gJ,EH∈C1×N和gJ,E∈C1×N，IRS 反射基站信号到IoT 设备、EHR 和Eve 的信道增益分别为hI,U∈C1×M、hI,EH∈C1×M和hI,E∈C1×M，IRS 反射干扰机信号到IoT 设备、EHR 和Eve 的信道增益分别为gI,U∈C1×M、gI,EH∈C1×M和gI,E∈C1×M。IRS 调整其反射元素相位角以最大化用户组合方式入射信号。IRS 的对角相移矩阵表示为，主对角线θn=(0，2 π)表示组合入射信号第n个元素的相移，其中，n=1,2,…,N。假设所有的信道增益均采用理想CSI 模式，且均采用准静态平坦衰落信道模型[27]。基站的发射信号为

3 安全波束成形设计方案

本节通过联合优化安全发射波束成形矢量、干扰协方差矩阵和IRS 相移，以实现在基站发射功率、干扰发射功率和IoT 可达保密速率约束条件下EHR的能量采集最大化。

3.1 问题建模

能量采集最大化问题可以表述为P1。

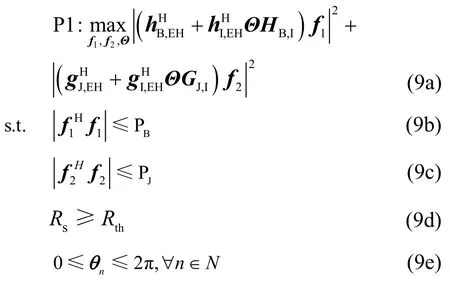
其中，Rth为保密速率阈值。由于目标函数以及约束条件的非凸性[27]，P1 是一个具有二次型约束的非凸二次型规划问题（QCQP,quadratically constrained quadratic program），也是NP-hard 问题，求解困难。但是当f1,f2和Θ中的一个变量已知时，P1 可以利用交替迭代算法有效地求解。

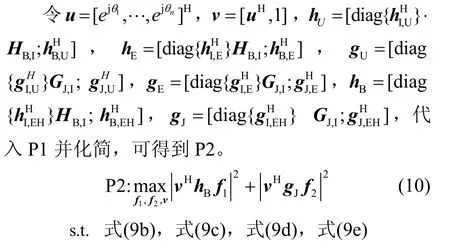
由于保密速率约束条件式(9d)是非凸的，可以采用松弛变量和SPCA 进行凸近似。为使约束条件式(9d)易于处理，首先引入2 个松弛变量r1>0和r2>0，式(9d)可以等价转化为

根据凸优化理论[28]，约束条件式(14a)和式(14b)仍为非凸的，但其右半部分分别是关于变量f1和f2的二次型除以线性的凸函数形式。根据文献[29]中的SPCA[28]的思想，二次型除以线性函数的形式能够等价转化为一阶泰勒展开式。

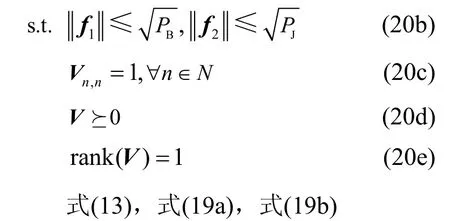
由于组合变量(f1,f2)与V仍然存在耦合，P3的目标函数式(20a)仍然非凸。采用交替迭代算法[24]，将P3 转化为2 个子问题，再分别利用SPCA 和SDR求得子问题的解。

3.2 交替迭代算法

根据文献[28]，P4 是二阶锥规划问题，可以通过CVX 工具[31]直接求解。因此，本文提出一种SPCA 迭代算法求解子问题P4，具体流程如算法1所示。

给定组合变量(f1,f2)，优化向量V。P3 可转化为P5。

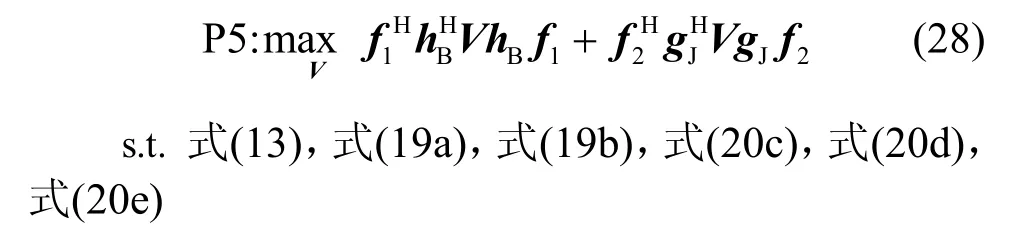
由于存在秩一约束，P5 仍然非凸。采用SDR算法[30]，忽略Rank(V)=1 的约束条件，P5 可转化为P6。

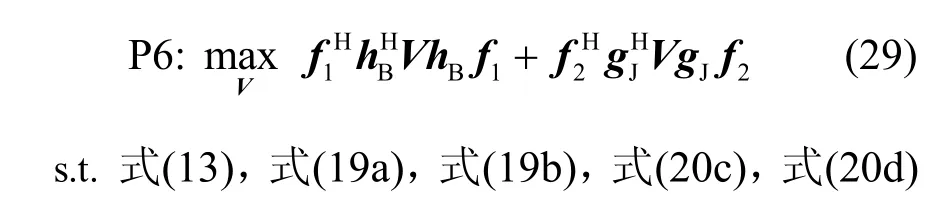
根据文献[28]，P6 是一个SDP 问题，可采用凸优化求解器CVX[31]进行求解。然而，一般来说，松弛问题P6 不一定得到秩一解，即Rank(V)≠1，P6 的最优目标函数值仅服务于P5 的上界。因此，从P6 的最优高阶解中构造秩一解需要额外步骤。具体来讲，首先通过对V=UΣUH进行奇异值分解，其中，U=[e1,…,eN+1]和Σ=diag(λ1,…,λN+1)分别是一个酉矩阵和对角矩阵。然后，获得P5 的次优解。其中，r∈C(N+1) ×1是根据r～CN(0,IN+1)生成的随机向量。CN(0,IN+1)表示均值为零的圆对称复高斯分布，协方差矩阵为IN+1。利用独立生成的高斯随机向量r，将P6 的目标函数的值近似为所有r中最优v所得到的最大值。最后，v可以通过式(30)获得。

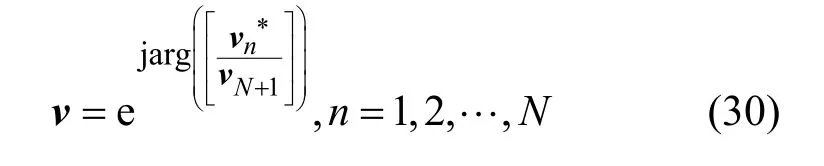
结果表明，SDR 加上多次执行随机化保证了P6 目标值的最大化[33]。

使用交替迭代算法的思想求解原优化问题P3，迭代过程中EHR 采集到的功率单调递增，但由于发射功率的有界性，所提的交替迭代算法最终将收敛于一个恒定值。然而，由于原优化问题P1 非凸，该算法不能保证获得全局最优解，所提交替迭代方法逐渐逼近最优解。定义和E(t)分别为交替迭代算法中第t次迭代后的解。具体交替迭代算法流程如算法2 所示。

算法2交替迭代算法

4 仿真测试与分析

本节通过仿真分析评估所提方案的性能。采用以下3 种基准方案进行对比。1) 使用IRS，随机相移，即从区间中随机选取θn；2) 不采用IRS，即θn=0；3) 使用IRS，不采取协同干扰，即非Jammer方案。在仿真中，假设所有信道均采用瑞利衰落信道模型，IRS 的位置通常要避免阻塞来自基站的信号；假设基站/干扰机至EHR、Eve、IoT 的距离分别为5 m、90 m、100 m；基站/干扰机至IRS 信道为视距链路，距离设为7 m；IRS 至EHR、Eve、IoT的信道也为视距链路，且距离分别为3 m、85 m、95 m[34]。该系统的具体部署如图2 所示，其他仿真参数如表1 所示。

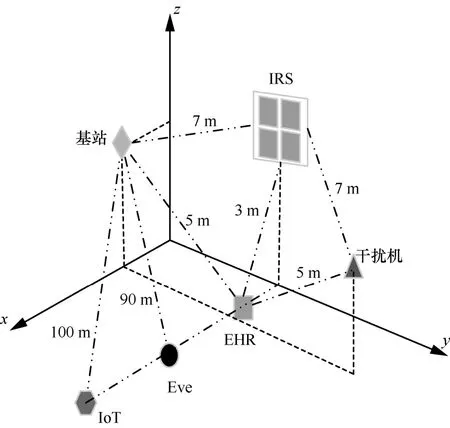
图2 系统具体部署

表1 仿真参数设置

图3 给出了所提交替迭代算法获得的EHR 的采集能量随迭代次数变化曲线。从图3 中可知，所提交替迭代算法的收敛速度快，在不同PB下仅需5 次迭代就能获得最大的采集能量，达到收敛。

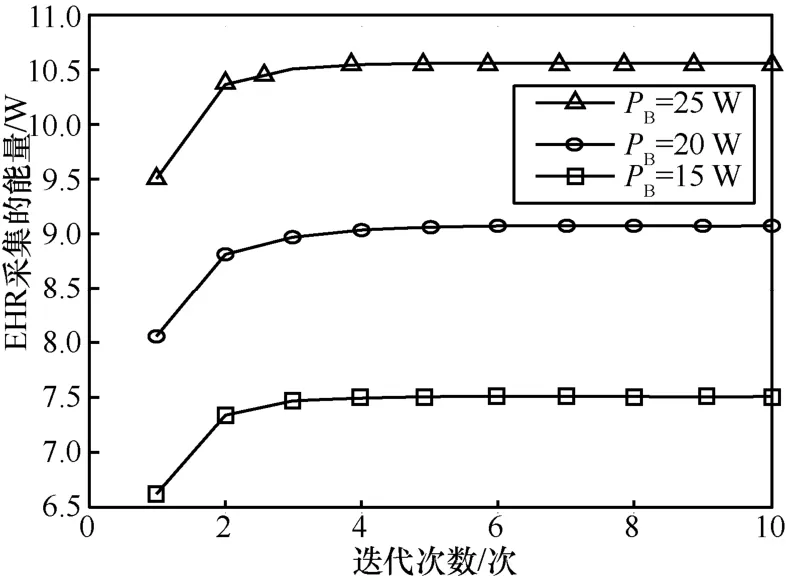
图3 EHR 的采集能量随迭代次数变化

图4给出了EHR采集的能量与保密速率的对比关系。在M=8和N=40时，从图4 中可得，随着保密速率的提高，EHR 采集的能量会逐渐下降；将本文所提方案的能量采集与3 种基准方案进行对比，在IRS的辅助下采集的能量优于非IRS 方案约2.88 dB，主要原因是IRS 为系统提供了新的自由度和分集增益，通过优化IRS 的相移提高了EHR 采集的能量。本文所提方案优于非IRS 方法和随机相移的方法。对比非Jammer 方案，图4 验证了本文所提方案的有效性，在相同保密速率情况下，本文所提方案采集的能量更多。

图5 给出了EHR 采集的能量与IRS 反射元素数量N的关系曲线。显然，当本文所提方案优于其他基准方案。假设Rth=3 bit/(s.Hz)，当IRS 反射元素数量从10 个增加到70 个时，本文所提方案中EHR 采集的能量随着反射元素数量N的增加单调增加。主要原因是，随着IRS 反射元素数量N的增加，IRS 所获取空间自由度和分集增益将N变大。当N=10 时，非Jammer 方案采集的能量略低于随机相移方案，原因在于非Jammer 方案总功率低于随机相移方案；当N>15 时，非Jammer 方案优于随机相移方案。与非IRS 方案相比，随机相移方案仅获得微小的性能增益，随着N的增加，性能提升较慢。

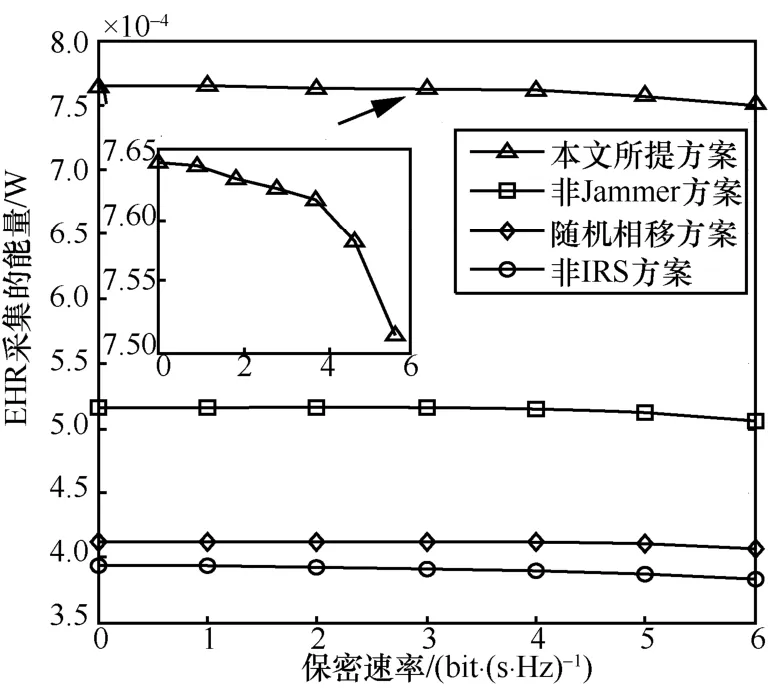
图4 EHR 采集的能量与保密速率的关系

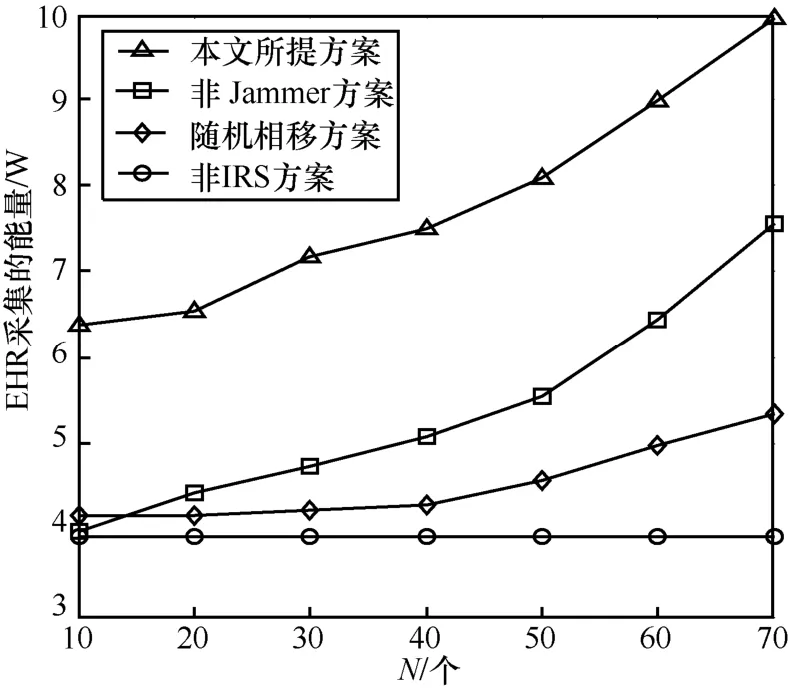
图5 EHR 采集的能量与IRS 反射元素数量N 的关系

图6 给出了EHR 采集的能量与基站发射功率的关系曲线。从图6 中可以看出，随着基站发射功率的增加，EHR 采集的能量关于基站发射功率单调递增。基站功率相同情况下，本文所提方案优于非Jammer 方案约1.74 dB。对比分析可知，IRS 辅助的系统带来能量采集性能的增益优于非IRS 方案，本文所提方案显著优于随机相移方案。另外，随PB 增加，IRS 方案与非IRS 方案的性能差异以及IRS 相移优化方案与随机相移方案的性能差异逐渐增大，原因在于本文所提方案会定向增强期望反射信号，进而增大了IRS 带来的空间自由度和分集增益。

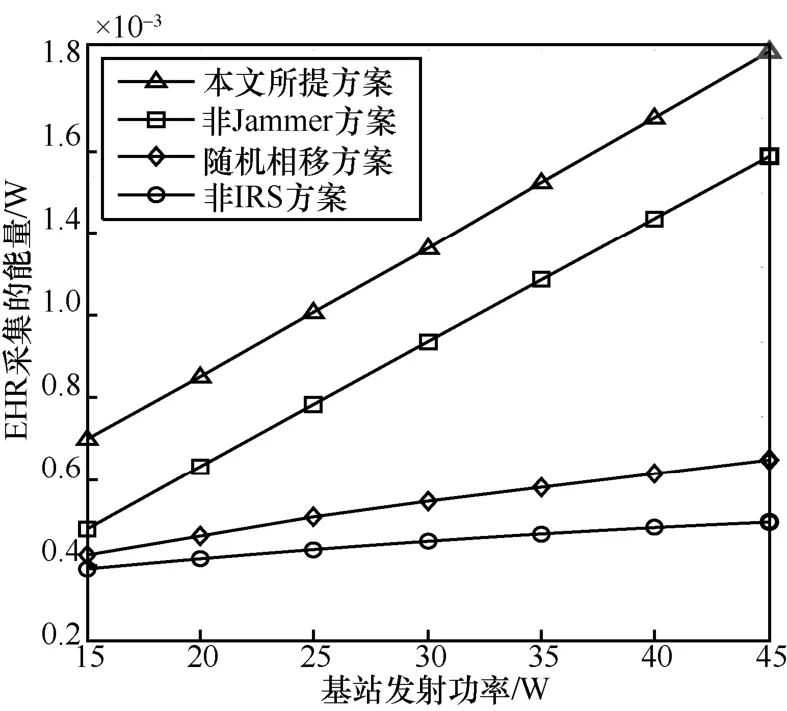
图6 EHR 采集的能量与基站发射功率的关系

5 结束语

根据IRS 定向增强反射信号以及干扰机的特点，针对基于IRS 辅助的SWIPT IoT 系统，本文提出一种安全波束成形设计方案。在满足保密速率、发射功率和IRS 反射相移约束下，通过联合优化发射波束成形矩阵、干扰协方差矩阵和IRS 反射相移矩阵，最大化EHR 的能量采集；利用交替迭代算法、松弛变量、辅助变量、分式优化理论将原优化问题转化为2 个子问题，并采用SPC 和SDR 求得子问题的可行解；提出一种SPCA 迭代算法和交替迭代算法。最后，通过仿真结果验证以下3 个结论：1) 所提的交替迭代算法仅需5 次迭代就能达到最大采集能量；2) IRS 辅助的系统方案能量采集性能要优于非IRS 方案；3) 对IRS 反射相移的优化能够显著提升系统的能量采集性能。