类MARS 密码结构的线性特性及其优化设计

王念平，洪礼荣

（信息工程大学密码工程学院，河南 郑州 450001）

1 引言

线性密码分析是Matsui[1]在1993 年欧洲密码年会上提出的一种针对迭代型分组密码的已知明文攻击方法，其基本思想是利用分组密码算法中明文、密文和密钥之间的不平衡线性逼近来恢复某些密钥比特。对分组密码而言，线性密码分析经过不断的丰富与发展，已成为最有效的密码分析方法之一。因此，评估分组密码抵抗这一攻击的能力是分组密码设计中必须考虑的问题。

在对分组密码抵抗线性密码分析的能力进行评估时，通常的做法是估计多轮线性逼近中活动轮函数（即输出线性逼近非零的轮函数）或活动S 盒（即输出线性逼近非零的S 盒）个数的下界，进而给出最大线性逼近概率的上界。如果该上界足够小，就可以认为分组密码具有较强的抵抗线性密码分析的能力。因此，活动轮函数或活动S 盒的个数是评估分组密码抵抗线性密码分析能力的重要指标。

MARS 密码结构[2-4（]如图1 所示）是一种典型的密码结构，例如 AES（advanced encryption standard）竞赛的5 个最终候选算法之一的MARS[2]就采用了这样的结构。针对MARS 密码结构，人们进行了深入的研究。文献[3]研究了MARS 密码结构的随机性。文献[5-7]对MARS 密码结构或嵌套代替−置换网络（SPN,substitution-permutation network）的MARS 密码结构抵抗线性密码分析的能力进行了详细的分析。文献[8]利用不可能差分归一化（UID,unified impossible differential）方法找到了广义MARS 密码结构的11 轮不可能差分。文献[9]研究了类MARS 密码结构的不可能差分，证明了n分支类MARS 密码结构存在3n− 1轮不可能差分，且当n是奇数时，任意轮结构均存在不可能差分。文献[10]进一步研究嵌套SPN 结构的类MARS 密码结构，将不可能差分的长度扩展至12 轮，且这个结果与轮函数和扩散层的结构无关。文献[11]针对嵌套SPN 结构的MARS 密码结构，利用计算机搜索算法找到了1～21 轮差分特征中活动S 盒个数的下界，并指出该算法可直接用于线性密码分析，即通过考虑对偶结构来计算线性逼近中活动S 盒个数的下界。文献[12]证明了MARS 密码结构和SMS4 密码结构[4]之间存在差分−线性对偶性，再结合文献[13]对SMS4 密码结构的评估结果，给出目前针对MARS 密码结构的多轮线性逼近中活动轮函数个数下界的最新理论成果。具体地，对于 MARS 密码结构，当轮函数是双射时，5i+j(i≥0,0≤j≤4)轮线性逼近至少有个活动轮函数，其中表示不大于x的最大整数（下同）。

图1 MARS 密码结构

现在的问题是对于如图1 所示的MARS密码结构，如果将其中的线性变换（即循环左移变换）用{0,1}4上的某个线性双射（对应于某个4 阶0,1 可逆矩阵）代替，那么活动轮函数个数的下界可能达到的最大值是多少？另外，能否找到一种线性双射，使活动轮函数个数的下界达到或接近可能的最大值？基于这种想法，本文提出了类MARS 密码结构，如图2 所示，研究了该密码结构的线性特性，并给出了线性变换的一种优化设计方法。这里所说的类MARS 密码结构是指每一轮中的线性变换从{0,1}4上的线性双射（对应于4 阶0,1 可逆矩阵）中选取。在此特别指出，每一轮中的线性变换从{0,1}4上的线性双射中选取并不是说{0,1}4上的每一个线性双射都是合适的。例如，恒等映射作为每一轮中的线性变换显然就不合适。事实上，在实际的密码设计中，每一轮中的线性变换一般从那些性能较好的、合适的线性双射中选取。

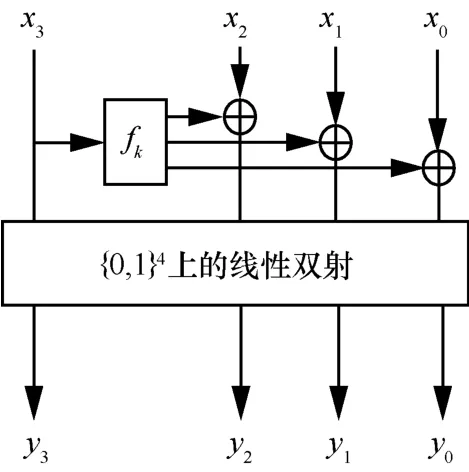
图2 类MARS 密码结构

本文的研究结果表明，对于类MARS 密码结构，每一轮中的线性变换只要从{0,1}4上的线性双射中选取，无论怎样设计线性变换，t(1≤t≤ 3)轮线性逼近中都至少有一条线性逼近，其活动轮函数的个数为0；4 轮线性逼近中至少有一条线性逼近，其活动轮函数的个数 ≤ 1；t(t>4)轮线性逼近中至少有一条线性逼近，其活动轮函数的个数≤8t/15。这些线性逼近是由类MARS 密码结构本身决定的，或者说是固有的线性特性。在此基础上，本文给出了线性变换的一种优化设计方法，该优化设计使活动轮函数个数的下界与MARS 密码结构相比更加接近可能的最大值。

2 预备知识

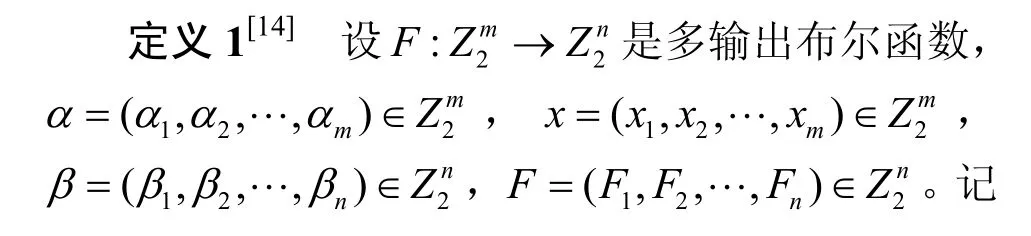
3 类MARS 密码结构的线性特性分析

首先，给出3 个引理。

定理2 实际上是说，无论每一轮中的线性变换怎样设计，t(t>4)轮线性逼近的活动轮函数个数的下界≤。

为方便起见，将定理1 和定理2 合写成定理3。

定理3对于图2 所示的类MARS 密码结构，t(t≥ 1)轮线性逼近中至少有一条线性逼近，其活动轮函数的个数≤L(t)。其中

由定理3 知，无论每一轮中的线性变换怎样设计，t(t>4)轮线性逼近的活动轮函数个数的下界都小于或等于L(t)。

4 线性变换的一种优化设计

本节给出类MARS密码结构中线性变换的一种优化设计方法，该优化设计使活动轮函数个数的下界与MARS 密码结构相比更加接近可能的最大值L(t)。

图3 是一类特殊的类MARS 密码结构，其中虚线方框部分表示线性变换。由图3 可知，其1 轮输入与输出的关系式可以表示为

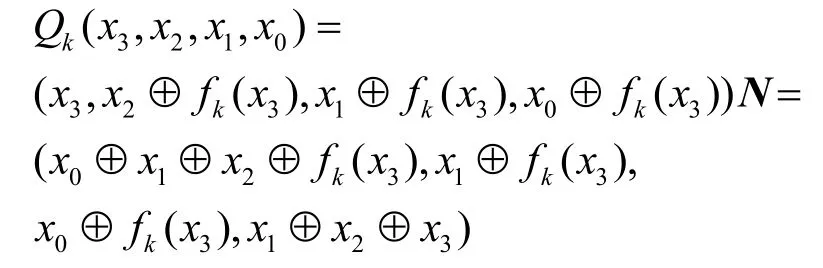
其中，k表示轮密钥，⊕表示异或运算，fk表示轮函数，N表示线性变换（即图3 中虚线方框部分）所对应的4 阶0,1 可逆矩阵，N。

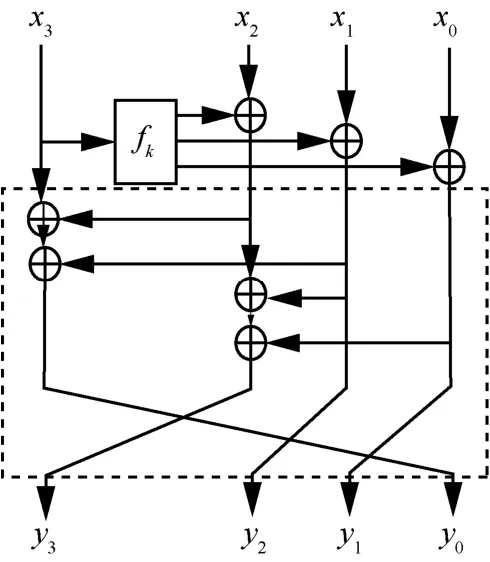
图3 一类特殊的类MARS 密码结构

为了直观起见，针对1～32 轮的情形，将MARS密码结构（如图1 所示）、一类特殊的类MARS 密码结构（如图3 所示）的活动轮函数个数的下界与定理3 中L(t)的值进行比较。其中，MARS 密码结构的下界是指图1 所示的MARS密码结构的活动轮函数个数的下界，该结果由文献[12-13]可得。特殊的类MARS密码结构的下界是指图3 的一类特殊的类MARS 密码结构的活动轮函数个数的下界，该结果可利用与文献[13]类似的推导方法得出，在此不再赘述。

2 种密码结构的活动轮函数个数的下界与L(t)的比较如表1 所示。由表1 可以看出，当线性逼近的轮数较大时，MARS 密码结构的活动轮函数个数的下界与L(t)相比有较大的差距。例如，当线性逼近的轮数 ≥ 21时，二者的差值 ≥ 3；当线性逼近的轮数≥ 27时，二者的差值 ≥ 4；当线性逼近的轮数为32时，二者的差值为5。但这类特殊的类MARS 密码结构的活动轮函数个数的下界与L(t)更加接近。当线性逼近的轮数为6、17、19、20、21、23、25、30、31 和32 时，二者的差值为2；当线性逼近的轮数为5、7、8、9、10、11、12、15、16、18、22、24、26、27 和29时，二者的差值为1；其他情形下二者的差值为0。

以上分析结果表明，从抵抗线性密码分析的角度来讲，这类特殊的类MARS 密码结构中的线性变换设计得较好。从应用层面来讲，当轮数 ≥ 12时，这类特殊的类MARS 密码结构的活动轮函数个数的下界比MARS 密码结构的活动轮函数个数的下界要大，这意味着与MARS 密码结构相比，采用这类特殊的类MARS 密码结构的密码算法可以在更少轮数内达到足够的安全强度。从实现效率来讲，这类特殊的类MARS 密码结构仅增加了少许异或运算，对于算法的实现效率影响不大。

实际上，图3 中的线性变换（即虚线方框部分）仅仅是一种优化设计方法。除此之外，还有其他的优化设计方法，使在相同的轮数下，活动轮函数个数的下界与MARS 密码结构相比更接近于L(t)（L(t)的含义见定理3）。例如，将图3 中的线性变换用它的逆变换代替，也可以得到相同的活动轮函数个数的下界。从道理上讲，通过分析全部可能的线性变换，就可以找到类MARS 密码结构中线性变换的最优化设计，但由于异或运算“⊕”的影响，使搜索到的活动轮函数个数的下界比实际的下界可能要小，因此不能确定图3 中的线性变换是否最优。如何寻找类MARS 密码结构中线性变换的最优化设计，还需要进一步的探讨。另外，本文的研究结果表明，无论类MARS 密码结构中的线性变换怎样设计，多轮线性逼近中活动轮函数个数的下界都不可能超过某个值，这些特性是由类MARS 密码结构本身决定的，它揭示了类MARS 密码结构固有的线性特性，这种研究方法对其他分组密码结构的研究也具有一定的借鉴意义。例如，用本文的研究方法可以证明，对类SMS4 密码结构（即将SMS4 密码结构中的线性变换用{0,1}4上的线性双射代替），也有与定理1～定理3 类似的结论成立。

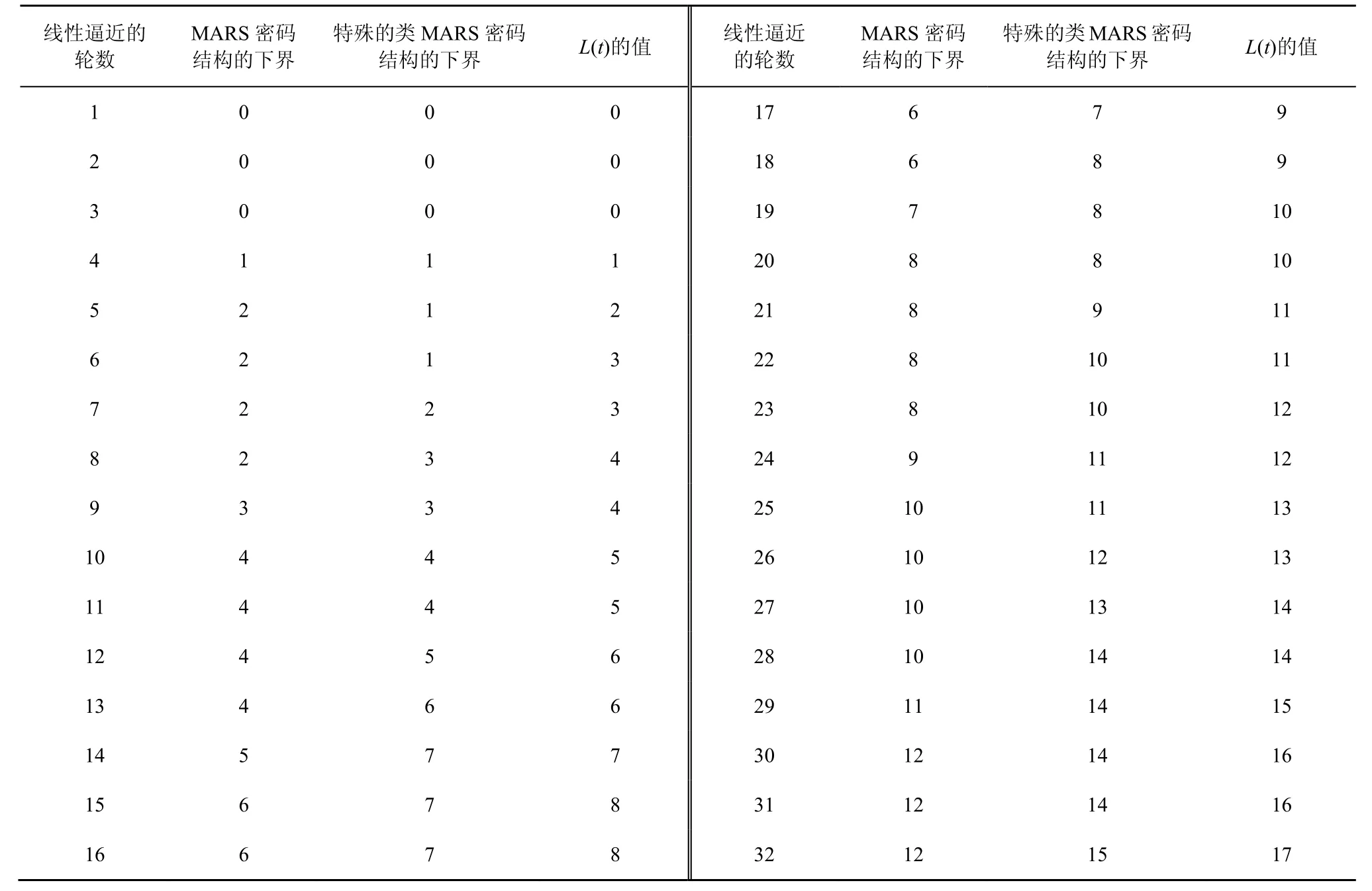
表1 2 种密码结构的活动轮函数个数的下界与L(t)的比较

5 结束语

本文提出了类MARS 密码结构，通过分析一类具有特殊结构的线性逼近的传递规律，给出了该密码结构的若干线性特性。具体地，不论每一轮的线性变换怎样从{0,1}4上的线性双射中选取，t(1≤t≤ 3)轮线性逼近中至少有一条线性逼近，其活动轮函数的个数为0；4 轮线性逼近中至少有一条线性逼近，其活动轮函数的个数不超过1；t(t>4)轮线性逼近中至少有一条线性逼近，其活动轮函数的个数不超过。在此基础上，给出了类MARS 密码结构中线性变换的一种优化设计方法，该优化设计使活动轮函数个数的下界与MARS 密码结构相比更加接近可能的最大值L(t)（L(t)的含义见定理3），从抵抗线性密码分析的角度来讲，该线性变换设计得较好。