基于Pignistic 概率转换和奇异值分解的证据冲突度量方法

郭兴林，孙振晓，周昱瑶，漆莲芝，张谊

（中国工程物理研究院计算机应用研究所，四川 绵阳 621900）

1 引言

DS 证据理论被广泛用于信息融合领域，然而Zadeh[1]指出在证据存在高冲突时，直接使用证据理论进行融合可能得出有悖于常理的结论。针对证据冲突的情况，主要的解决办法分为2 类[2]，一类是对冲突证据进行预处理[3-6]，消除或降低证据间的冲突性；另一类是修改证据合成规则[7-13]，将证据间冲突进行再分配。这2类方法均需要对证据间冲突进行准确度量。

国内外学者针对证据冲突度量进行了大量研究，Jousselme 等[14]给出了集合的相似性定义，采用证据间距离衡量证据冲突度。杨风暴[15]给出了证据一致度、证据冲突度、证据冲突强度、证据冲突/一致度等参数描述证据冲突程度。Liu[16]采用Pignistic概率转换定义了证据间Pignistic概率距离，将其作为证据间冲突度量指标。蒋雯等[17]改进了Jousselme 距离冲突度量方法，将Jousselme 距离和冲突因子联合，取其均值作为新的冲突因子。柯小路等[18]通过构建证据基本概率分配（BPA,basic probability assignment）矩阵，对其进行奇异值分解，利用最小奇异值表示证据间冲突。宋亚飞等[19]在分析证据相关性与冲突关系的基础上，给出了基于证据相关系数的冲突判定准则。包甜甜等[2]采用交叉熵表示证据的散度，通过Hamacher T–余范融合证据距离和证据散度来度量证据间冲突。上述方法在部分冲突场景下具有较好的适应性，一定程度上弥补了经典冲突因子的缺陷，但仍存在一些不足。为此，本文提出了一种基于Pignistic 概率转换和奇异值分解的证据冲突度量方法，能够较好地适应证据融合时可能出现的多种证据冲突场景。

2 DS 证据理论及其存在的问题

DS 证据理论是由 Dempster[20]提出，后经Shafer[21]扩充和发展形成的证据推理方法。

定义1设Θ为辨识框架，Θ的所有可能子集构成幂集2Θ。一个 BPA 函数定义为映射m:2Θ→[0,1]，满足[20]

例1设辨识框架{θ1,θ2}，证据E1、E2的基本概率函数m1、m2满足

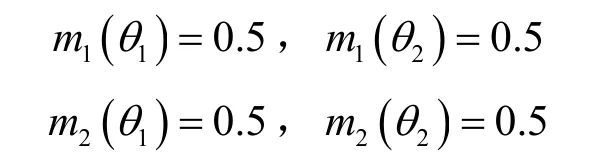
证据E1、E2是完全一致的，理论上证据冲突应该为0，而K度量结果为0.5，表示证据间存在较大冲突。正因为K仅局部反映了证据焦元间的非相容程度，导致K度量结果与实际情况不符。

3 常见证据冲突度量方法

针对经典的冲突因子K在部分证据冲突场景下存在冲突度量失准的问题，不少学者对证据冲突度量方法进行了深入研究，提出了一些改进方法，具有代表性的有以下几种。

定义3Jousselme 证据距离。假设辨识框架Θ下的有N个相互独立的元素，m1、m2是证据E1、E2的基本概率分配函数，其焦元分别为Ai、Bj，则m1、m2之间的Jousselme 距离可以表示为[14]

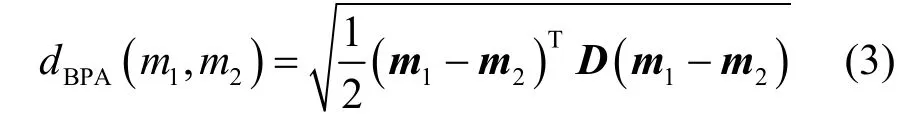
其中，m1、m2是由m1、m2构成的2N维列向量；D是焦元关联矩阵，为2N× 2N的正定系数矩阵，其元素可表示为

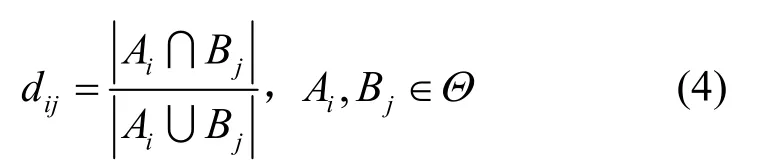
定义4Pignistic 概率距离。设m1和m2是辨识框架Θ下证据E1和E2的基本概率分配函数，BetPm1和BetPm2分别为其Pignistic 概率转换，则Pignistic 概率距离定义为[16]

其中，Pignistic 概率转换函数定义为

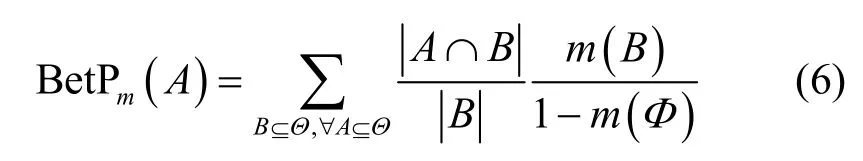
Pignistic 概率距离描述证据间对于不同焦元支持程度的最大差异。

定义5联合冲突度量因子。设任意两证据间Dempster 冲突因子为Kij，Jousselme 证据距离为dBPA(mi,mj)，联合冲突度量因子定义为[17]

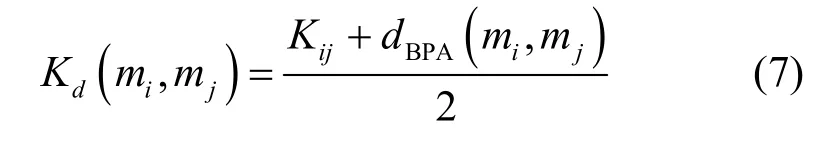
定义6相关系数。设m1和m2是辨识框架Θ下证据E1和E2的基本概率分配函数，m1和m2之间相关系数定义为[19]

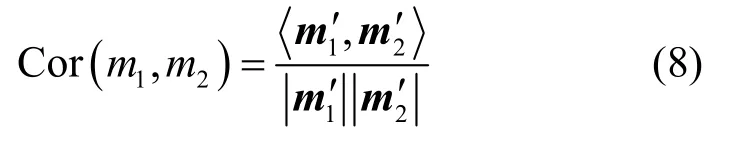
定义7最小奇异值。设m1和m2是辨识框架Θ下证据E1和E2的基本概率分配函数，对应的焦元集为A和B，记C=A∪B={C1,C2,…,Cm}，则可定义如下BPA 矩阵[18]

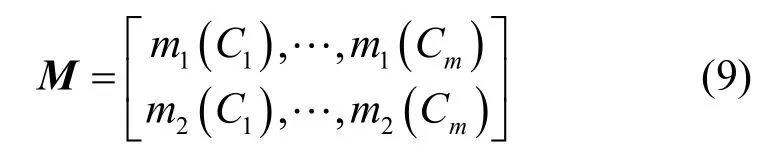
则证据冲突量定义为

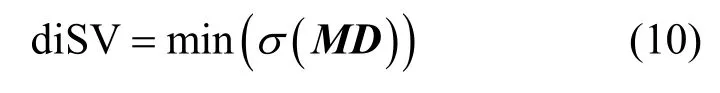
其中，σ(MD)表示对MD矩阵进行奇异值分解后得到的奇异值，直接选取最小奇异值用于度量证据间冲突。

4 新的证据冲突度量方法

证据冲突本质上可理解为证据对焦元信任的差异。在证据理论框架下，两方面的原因导致证据间存在冲突[23]：一方面是证据源可靠性不足导致证据信度存在差异，例如专家主观判断存在误差、传感器抗干扰能力不足等；另一方面是由于对事物认知不充分导致辨识框架不完整，证据给出支持多子集命题甚至完全未知的结论。综上所述，证据冲突表现在定量信度和定性焦元差异2 个层面，对二者进行充分考虑是准确度量证据冲突的关键。

4.1 Pignistic 概率转换构建证据复合信任函数矩阵

Jousselme 等[14]提出的焦元关联矩阵D被广泛用于衡量证据焦元差异，如定义3、定义6 和定义7所示，其应用模式一般为

其中，M为广义的概率分配函数矩阵，M′为矩阵转换后的信任函数矩阵，其元素可表示为

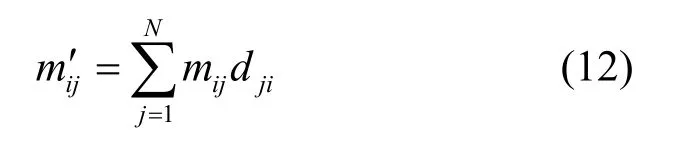
从式(12)可以看出，D的本质作用是在各相容、互斥焦元之间进行基本概率映射，将证据焦元差异映射到信度差异上去，但这种映射缺乏相应的理论支撑，物理意义并不明确。另外，由于D为正定矩阵，满足dij=dji，映射过程可能会引入干扰，破坏证据特征，造成冲突度量的准确性降低。例如，当焦元{θ2,θ3}向{θ1,θ2}概率映射时会将其概率的13分配给焦元{θ1,θ2}，反之亦然，概率转换的比例意义不明确。又如，在焦元{θ1,θ2}向θ1概率映射过程中，会将{θ1,θ2}信任的12 分配给θ1，这种映射类似于Pignistic 概率转换，反之，在焦元θ1向{θ1,θ2}概率映射过程中，同样会将θ1信任的12 分配给{θ1,θ2}。类似的映射虽然在一定程度上可以将焦元差异反映到信度差异上，但同时可能会引入干扰，造成算法度量性能下降。

为了能准确充分地反映证据焦元差异，同时不引入干扰，采用具有概率论和集合论支撑的Pignistic 概率转换[8]，将焦元差异映射到信度差异上，其矩阵形式可表示为

其中，P表示焦元概率转换矩阵，pij表示焦元Bj向焦元Ai概率转换的转换系数。不同于D，P为非对称矩阵，pij是有方向性的，pij定义为

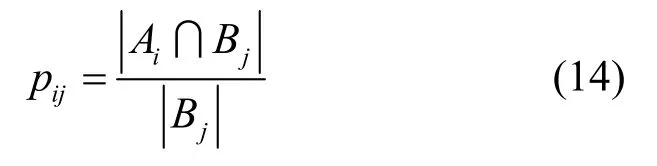
转换后M′的行向量即为原BPA 经Pignistic 概率转换的信任函数，实现了焦元差异向信度差异的有效映射。但由于Pignistic 概率转换会拓展证据的焦元集合，为原始证据不信任的焦元分配信任度，造成原始证据部分信息丢失，导致无法有效区分未知命题和同概率命题等情况。为了能充分表征证据差异特征，构建证据复合信任函数矩阵M′，M′满足

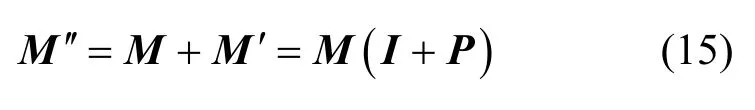
其中，I为n阶单位矩阵；M′中每个证据向量既包含原始的信度差异特征，也包含映射后的焦元差异特征。

4.2 基于奇异值分解的证据冲突度量因子

在衡量证据信度差异方面，现有方法易受证据信度分布离散程度的影响，难以有效反映证据特征。由于矩阵奇异值分解能够有效提取矩阵结构特征，本文提出了一种改进的基于奇异值分解的证据冲突度量方法，通过提取证据复合信任函数矩阵的奇异值来度量证据间的冲突情况。

定义8设任意2 个证据复合信任函数矩阵M′∈R2×n，M′中元素表示第i个证据对第j个焦元的信任程度，则存在正交矩阵U∈R2×2和V∈Rn×n，使[24]

考虑到证据复合信任函数矩阵的多变性、复杂性，其特征方向的个数及重要性都是不断变化的，且重要性具有一定的相对性。文献[18]仅将最小奇异值对应的特征方向作为冲突，而未结合矩阵的主要特征方向进行考虑，忽略了冲突与相似的相对性，具有一定的局限性。因此综合考虑证据矩阵相似特性和冲突特性，将矩阵空间划分为相似子空间S和冲突子空间N，相似子空间由奇异值最大的特征方向构成，表示证据矩阵的主特征方向，证据矩阵在该特征方向上是趋于相似的，冲突子空间由奇异值较小的特征方向构成，表示证据矩阵在这些特征方向上是冲突的。

定义9对于任意2 个证据构成的复合信任函数矩阵M′，其相似子空间S和冲突子空间N维数均为1，证据冲突度量因子定义为

其中，σmax、σmin分别为M′奇异值分解后的最大、最小奇异值；GSVD越大，表示证据间冲突越大。改进的冲突度量因子全面考虑了证据矩阵的结构特征，能够较好地对证据间冲突进行度量，具有以下性质。

5 算例分析

为了验证GSVD方法的冲突度量性能，在典型证据冲突场景下与常见方法进行了对比分析。由于dBPA、difBetP、Kd、Cor、diSV、GSVD仅定义了两两证据间的冲突，为方便计算，将证据集合两两间冲突的均值作为全局冲突。

5.1 全冲突场景及其扩展形式

例2以文献[15]算例为参照，设辨识框架Θ={θ1,θ2,θ3}，初始证据集合包含证据E1、E2，其BPA 分别为m1、m2，有m1(θ1)=1，m1(θ2)=0，m1(θ3)=0，m2(θ1)=0，m2(θ2)=1，m2(θ3)=0，向证据集合中添加新的证据Ei(i=3,4,…,N)，其BPA 函数为mi(θ1)=0，mi(θ2)=0，mi(θ3)=1，证据集合中证据数目共计N个，对N从2 增加到6 过程中各方法冲突度量结果进行统计，如表1 所示。

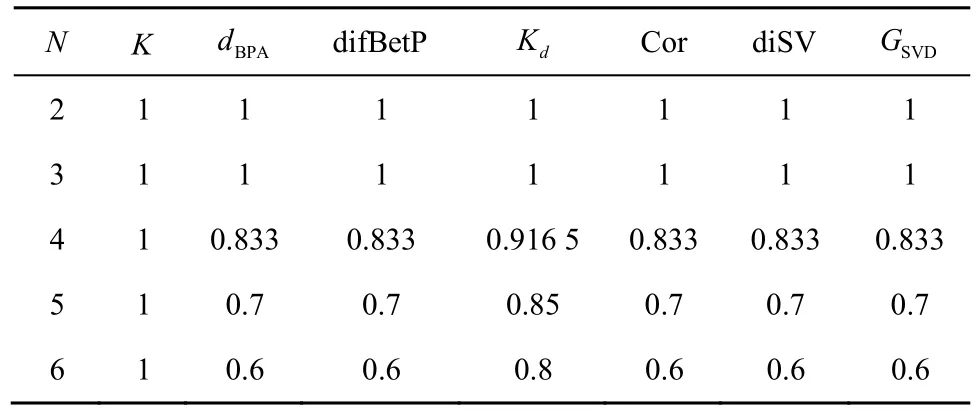
表1 全冲突场景冲突度量结果

当N=2,3时，证据分别完全信任不同的焦元，证据完全冲突，各方法均能正确度量。当N>3时，新加入的证据完全支持θ3，新的证据集合对θ3信任度持续增加，证据集合的一致性增强，证据间冲突应相应减小。从表1 中可以看出，K由于存在“一票否决”的特性，新加入的证据对θ3的支持度被m1(θ3)=0、m2(θ3)=0否决掉，导致在N变化过程中始终保持不变，与实际情况不符。dBPA、difBetP、Kd、Cor、diSV、GSVD方法随着N的增加，冲突度量结果呈递减趋势，趋势变化符合预期，且数值基本保持一致。

例3以文献[25]算例为基础扩展全冲突场景，设辨识框架，证据集合包含证据E1、E2，其BPA 分别为m1、m2，有m1(θj)=1/L，j=1,2,…,L，m2(θk)=1/L，k=L+1,L+2,… ,2L，m1、m2分别支持不同焦元，现逐渐调整L，对L动态变化过程中各方法冲突度量结果进行统计，如表2 所示。

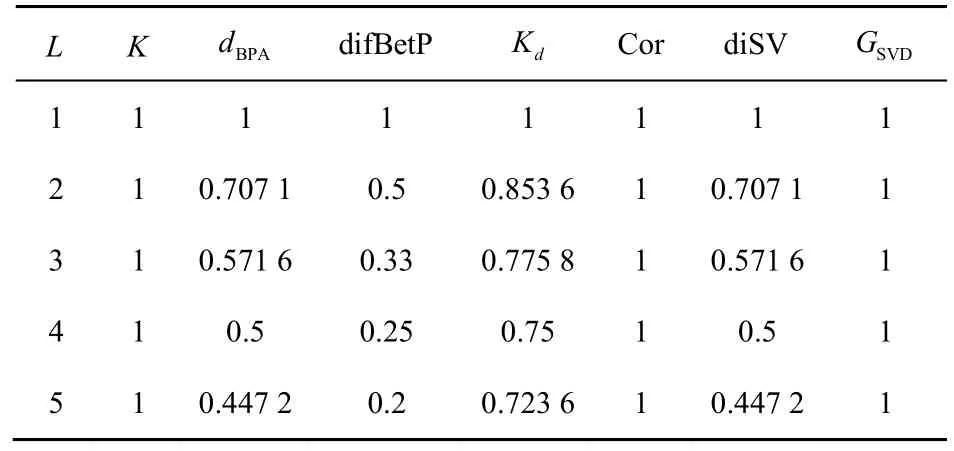
表2 全冲突场景扩展形式度量结果

在L变化过程中，两证据始终信任不同的焦元，且信任程度一致，证据完全冲突。从表2 可以看出，K由于仅关注证据的非相容性，度量恒为1，度量结果正确。根据dBPA、difBetP、Kd定义，3 种方法未考虑证据的一致性，度量结果会受证据信度离散程度的影响，随着L的增大，证据信度的离散程度增大，导致证据冲突降低，度量结果与实际不符。diSV 仅考虑最小奇异值σmin方向特征，未考虑其余特征，在证据完全冲突时，矩阵 2 个特征方向的重要性是一致的，即σmax=σmin，并且随着证据信度离散程度的增加，奇异值减小，导致冲突度量结果与实际不符。Cor、GSVD方法由于综合考虑了证据的差异性和相似性，冲突度量结果正确。

5.2 变信度场景

例 4以文献[1]算例为参照，设辨识框架Θ={θ1,θ2,θ3}，初始证据集合包含证据E1、E2，其BPA 分别为m1、m2，有m1(θ1)=0.9，m1(θ2)=0.1，m1(θ3)=0，m2(θ1)=0，m2(θ2)=0.1，m2(θ3)=0.9，现增加第3 条证据E3到证据集合中，其BPA 是动态变化的，m3初始状态等同于m2，m3的变化趋势分 为 2 个阶段，第一阶 段：m1(θ1)=ε，m3(θ3)=0.9−ε，m3(θ2)=0.1，增大ε直至m3(θ1)=m3(θ3)；第二阶段：m3(θ1)=0.45−ε，m3(θ2)=0.1+2ε，m3(θ3)=0.45−ε，增大ε直至m3(θ2)=1。对m3动态变化过程中各方法冲突度量结果进行统计，如表3 所示。

从表3 中可以看出，在m3为空，即只有2 个证据时，m1强烈信任θ1，m2强烈信任θ3，且都部分信任θ2，证据冲突较高，各方法都能较好地度量。当加入证据E3时，由于m3初始状态等同于m2，均强烈信任θ3，证据信任分布的一致性增强，证据间冲突相应减少。K受“一票否决”的影响，冲突反而增加，与实际不符。当m3在第一个阶段变化时，m3仍然主要支持θ3，但同时部分信任θ1，m3对m1支持性增加，证据集合间冲突持续减小。K、dBPA、difBetP、Kd度量结果保持不变，与实际不符。当m3(θ1)=m3(θ3)时，m3同时支持m1和m2，证据间冲突达到最小。当m3在第二阶段变化时，m3对θ2的信任持续增加，对θ1、θ3的信任逐渐减小，对证据E1、E2支持性减弱，证据冲突逐渐增大。当m3完全信任θ2时，3 个证据分别信任不同的焦元，证据间冲突达到最大。在m3动态变化过程中，Cor、diSV、GSVD度量结果变化趋势均能根据证据集合变化正确变化。

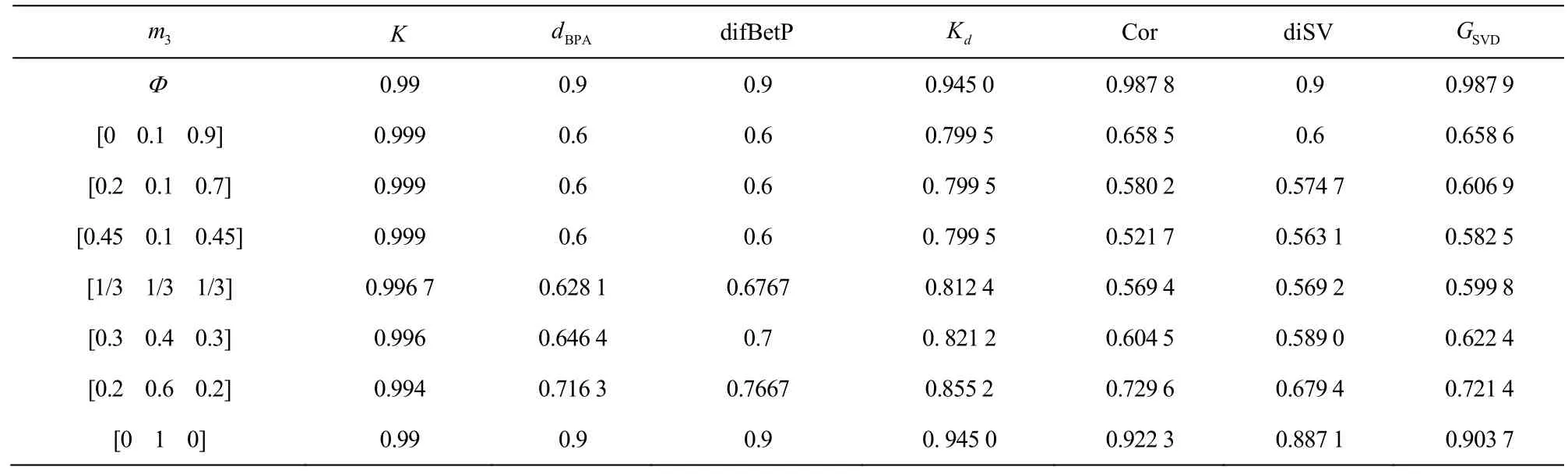
表3 变信度场景冲突度量结果

5.3 变焦元场景

例5以文献[19]算例为参照，设辨识框架，满足θi=i,i=1,2,…,20，证据集合包含证据E1、E2，其BPA 分别为m1、m2，m1满足m1({2,3,4})=0.05，m1({7})=0.05，m1(A)=0.8，m1(Θ)=0.1，其中A是Θ的子集，m2满足m2({1,2,3,4,5})=1，现调整m1中焦元A元素构成，A初始状态为{1}，每次递增一个元素直至变为Θ，A中元素个数为N，对N变化过程中各方法冲突度量结果进行统计，如表4 所示。

从表4 中可以看出，当焦元A中元素个数发生变化时，证据间一致性会发生变化，K方法度量结果在焦元A整个变化过程中始终恒定不变，与实际情况不符。在A从{1} 逐渐变化到{1,2,…,5}的过程中，2 条证据逐渐趋于一致，冲突性逐渐减小。当A等于{1,2,…,5}时，证据间一致性达到最大，证据间冲突达到最小。此后由于A变化到{1,2,…,20}过程中焦元元素数目增加，证据间一致性又逐渐降低，冲突也随之增大。dBPA、difBetP、Kd、Cor、diSV、GSVD方法冲突度量结果变化趋势正确，并且GSVD变化趋势更平缓。

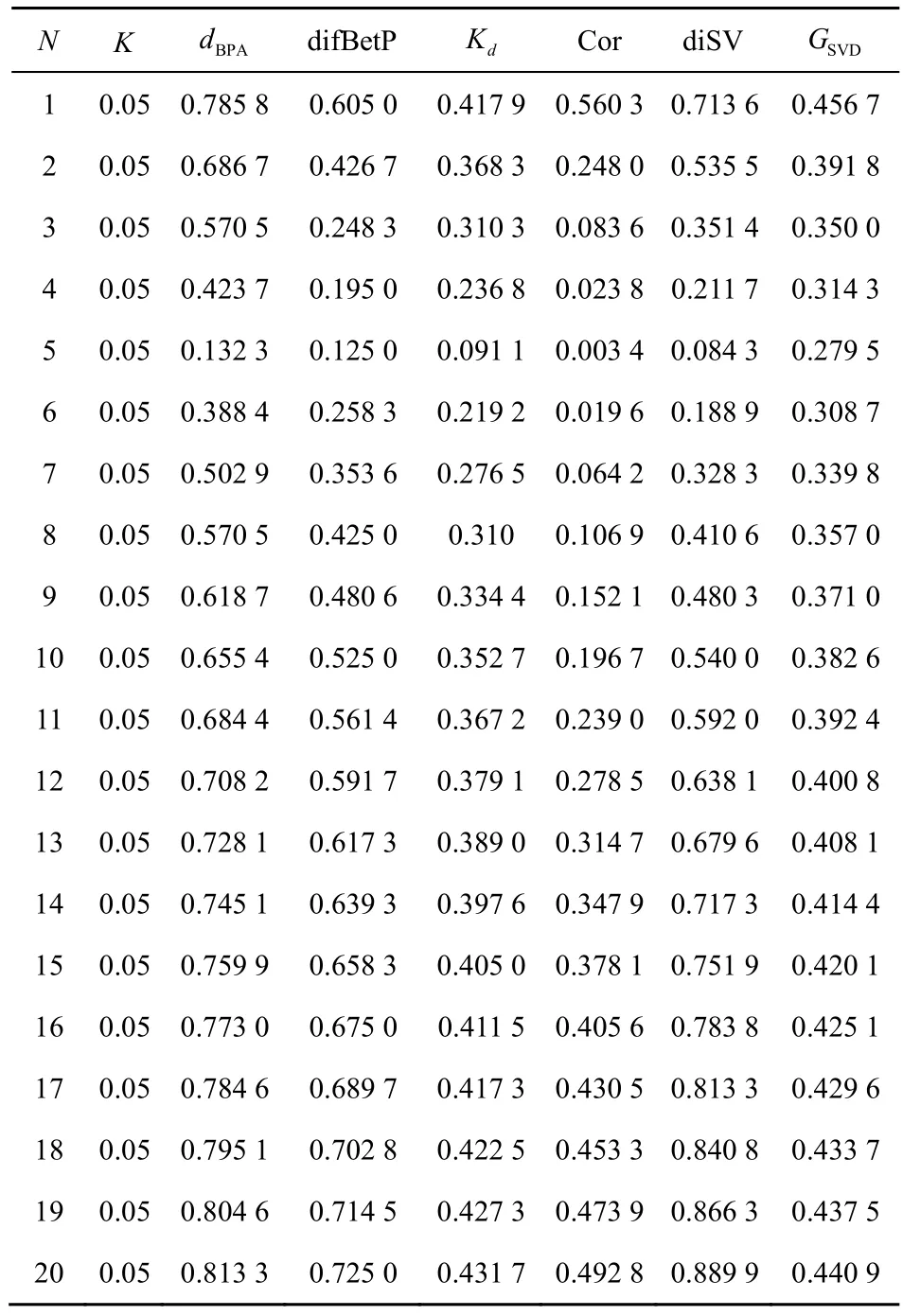
表4 变焦元场景-1 冲突度量结果

例6设辨识框架，证据集合包含证据E1、E2，其基本概率分配函数m1、m2初始状态为m1(A)=1，A={θ1,θ2,θ3,θ4,θ5}，m2(B)=1，B={θ6,θ7,θ8,θ9,θ10}，现同时按顺序调增焦元A、B中元素的数目，直到均变为Θ，焦元A、B中相同元素的数目为N，对N动态变化过程中各方法冲突度量结果进行统计，如表5 所示。

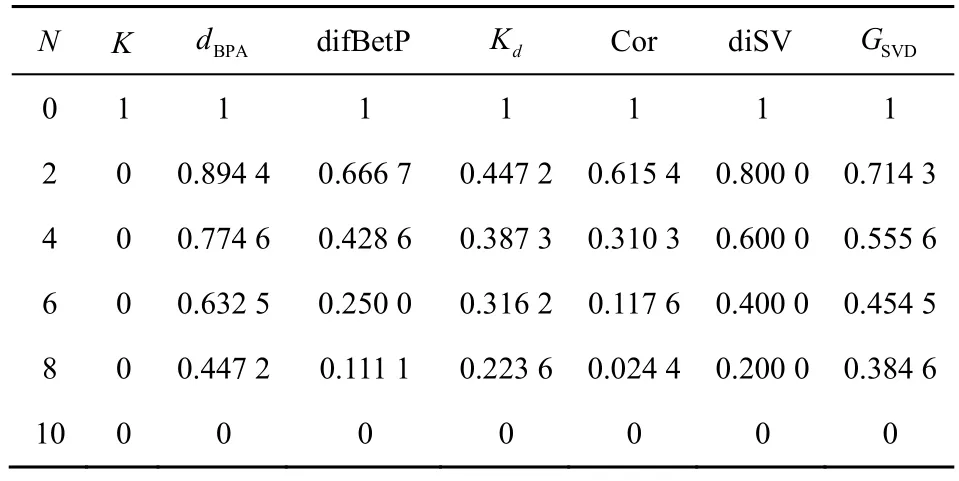
表5 变焦元场景-2 冲突度量结果

从表5 中可以看出，当证据为初始状态时，A、B焦元相同元素的个数为0，证据完全冲突，各方法度量结果均正确。随着N的增加，证据同时信任的元素增加，证据间的一致性增强，冲突逐渐减小。直到N=10，两证据完全相同时，证据间冲突变为0。由于K仅考虑到证据间非包容性，度量结果恒为0，与实际情况不符。dBPA、difBetP、Kd、Cor、diSV、GSVD方法冲突度量结果变化趋势正确。

5.4 焦元嵌套场景

例7以文献[14]算例为参照，设辨识框架，证据集合为E，相应的BPA 函数为mi，每一条证据只有一个焦元，且相互嵌套，即E1的焦元为{θ1}，E2的焦元为{θ1,θ2}，Ei的焦元 为{θ1,θ2,…,θi}，且mi满足mi({θ1,θ2,…,θi})=1，i=1,2,… ,N，对N从2 增加到10 过程中各方法冲突度量结果进行统计，如表6 所示。

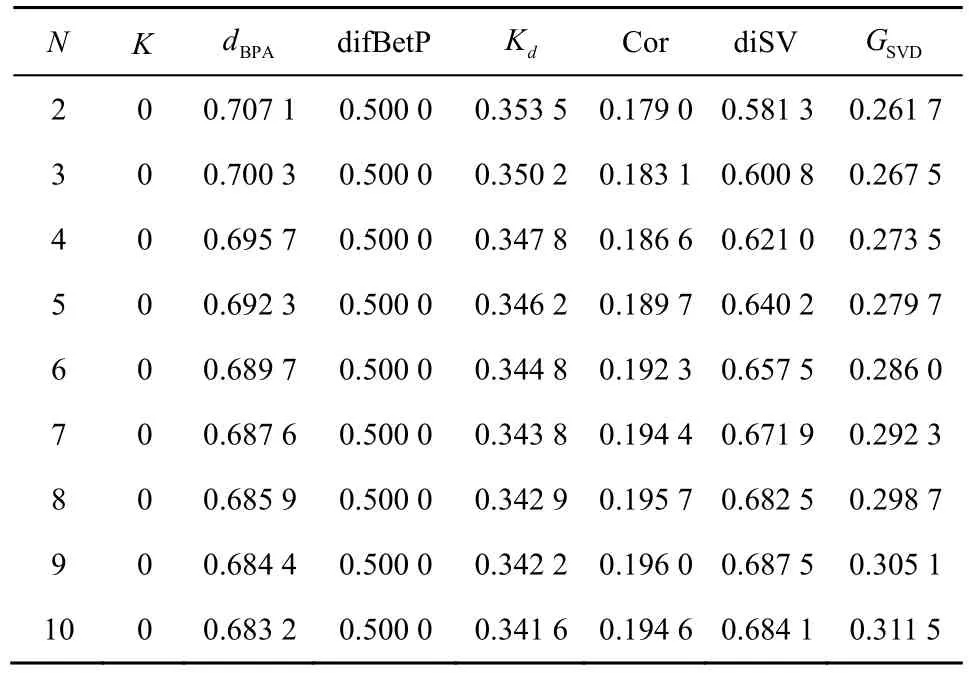
表6 焦元嵌套场景冲突度量结果

当N=2时，证据E1、E2焦元存在嵌套关系，即{θ1}⊆{θ1,θ2}，m1完全信任θ1，m2同时信任θ1和θ2，两证据具有一定的相似性，同时也存在一定的冲突。从表6 中可以看出，由于证据焦元是相容的，K方法度量结果为0，与实际不符，其余方法度量正确。当向证据集合加入证据Ei时，mi除了信任前i− 1条证据信任的{θ1,… ,θi−1}外，还部分信任前i− 1条证据否定的θi，证据间的冲突增大。随着N的持续增加，证据集合中冲突焦元逐渐增多，证据间的一致性降低，证据集合总的冲突度也逐渐增大。K保持恒定不变，与实际不符。dBPA、Kd由于焦元关联矩阵D会引起数据离散程度变化，随着mi支持的焦元元素数目的增多，经D映射后，证据信度的离散程度进一步增大，dBPA、Kd相应地减小，与实际不符。difBetP 方法仅考虑到焦元支持程度的最大差异，忽略了证据的相似性，陷入局部极值点，度量结果恒定不变，不符合实际情况。Cor、diSV 考虑了证据的差异性和相似性，但稳定性差，在2≤N≤ 9时，冲突度量结果逐渐增大，在N=10时，度量结果出现了减小的情况，与实际不符。在证据集合增长过程中，GSVD度量结果平稳增长，变化趋势与实际相符。

综上所述，相较于其他方法，GSVD方法能够适应更多的证据场景，且能够随着证据集合的变化动态地调整度量结果，度量结果准确性高，稳定性好。

6 结束语

证据冲突度量是制约证据理论运用效果的关键因素，针对目前常见冲突度量方法的不足，本文提出了一种基于Pignistic 概率转换和奇异值分解的证据冲突度量方法，通过Pignistic 概率转换构建证据复合信任函数矩阵，采用奇异值分解方法提取矩阵特征，并基于奇异值构建了新的冲突度量因子。算例分析表明，所提方法能够在全冲突场景、变信度场景、变焦元场景、焦元嵌套等多种证据场景下准确度量冲突，与常见方法相比，所提方法具有适应性广、准确性高、稳定好的优点。另外，本文仅给出了证据冲突的度量方法，如何依据冲突度量结果，对冲突证据进行预处理以及选择合适的证据合成规则是下一步的研究重点。