基于基扩展模型的改进正则化正交匹配追踪V2X 快时变SC-FDMA 信道估计

2021-05-13廖勇蔡志镕

通信学报 2021年4期

廖勇，蔡志镕

（重庆大学微电子与通信工程学院，重庆 400044）

1 引言

随着车联网[1-2]的快速发展，车联万物（V2X,vehicle-to-everything）通信已成为车载服务的关键技术[3-4]。V2X 主要包括车到基础设施（V2I,vehicle-to-infrastructure）、车到车（V2V,vehicleto-vehicle）和车到行人（V2P,vehicle-to-pedestrian）。V2X 作为智能交通系统（ITS,intelligent transportation system）中的重要部分，对ITS 的高效运转起着关键作用。针对车联网V2X 场景，在实际应用中用户对高可靠低时延通信（URLLC,ultra-reliable and low latency communication）[5]有极高的要求，这也是保障道路交通安全的重要因素。信道估计作为车联网V2X 通信中的关键处理技术受到了人们的广泛关注。目前，主流的支持V2X 通信的标准是C-V2X（cellular vehicle-to-everything），其采用了具有较低峰均比的单载波频分多址（SC-FDMA,single-carrier frequency-division multiple access）[6]。作为SC-FDMA 系统的关键技术，信道估计直接决定了通信的质量。在V2X 场景下，高速移动的车载终端会加剧多普勒效应，使信道快速变化，引起子载波间干扰（ICI,inter-carrier interference）[7]，并造成通信系统性能恶化，因此接收信号的正确译码必须依赖于高效且准确的信道估计。

传统的信道估计采用最小二乘（LS,least square）算法或线性最小均方误差（LMMSE,linear minimum mean square error）算法，忽略了高速移动场景下的ICI，限制了信道估计的精度[8]。针对此情况，更符合高速移动场景的基扩展模型（BEM,basic expansion model）被提出[9]。文献[10]提出一种基于BEM 的频域快时变信道估计算法，其利用信道频域时变传输函数辅助估计得到信道频域响应矩阵。文献[11]针对多输入多输出（MIMO,multiple input multiple output）通信系统，引入基于离散傅里叶变换的时空基扩展模型（ST-BEM,spatial-temporal basis expansion model）降低训练成本。文献[12]提出了一种基于BEM 和上行链路探测参考信号的快时变信道估计算法。

然而，上述研究中BEM 系数仍然主要采用LS估计，首先引入了噪声，其次没有充分利用BEM系数存在的稀疏性。针对此问题，并结合V2X 通信场景，本文提出一种面向高速快时变SC-FDMA系统的信道估计算法，主要贡献如下。首先，建立了高速信道冲激响应的BEM。其次，基于所建立的BEM，进一步证明了其系数具有稀疏性，将高速移动下的快时变信道估计问题转化为稀疏信号重构问题。针对该问题，本文搭建了基于SC-FDMA 的仿真通信系统，并提出基于BEM 的改进正则化正交匹配追踪（iROMP,improved regularized orthogonal matching pursuit）迭代稀疏信道估计算法，简称为BEM-iROMP 算法。BEM-iROMP 算法充分利用了基系数的稀疏性，在迭代步骤中根据反馈结果逐步提高估计的信道矩阵的精度。仿真结果表明，所提算法能够进一步提高信道估计的性能。

2 系统模型

2.1 基于BEM 的SC-FDMA 系统

在高速移动环境下，信道具有时变特性，高速移动产生的多普勒频移会引起SC-FDMA 系统子载波的频偏，从而导致SC-FDMA 系统子载波之间的正交性遭到破坏，严重影响系统性能。假设在SC-FDMA 系统模型中，有N个子载波，一个子帧包含I个SC-FDMA 符号。设发送第i个SC-FDMA符号上的第n个子载波符号为Xi(n),n∈[0,N− 1]，简写为Xi。Xi经过逆快速傅里叶变换（IFFT,inverse fast Fourier transform）进行SC-FDMA 调制后，有

其中，yi=[y(0),y(1),…,y(N−1)]T表示第i个SC-FDMA 符号上接收到的时域符号向量；zi为复加性白高斯噪声；hi为第i个SC-FDMA 符号的信道冲激响应矩阵，如式(3)所示。

其中，hi(k,l)表示在第i个SC-FDMA 符号时间内第l个抽头的第k个采样点的信道冲激响应。在接收端，时域接收符号yi经过快速傅里叶变换（FFT,fast Fourier transform）后可得到Yi。

其中，Hi表示第i个符号的频域响应矩阵，表示为

hi[k,l]可以进一步表示为

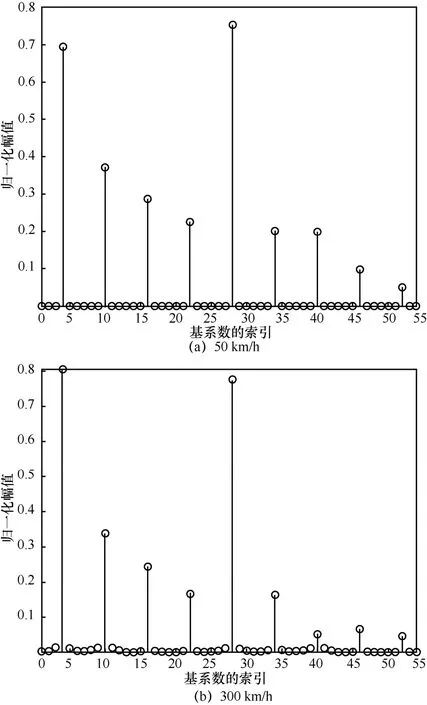
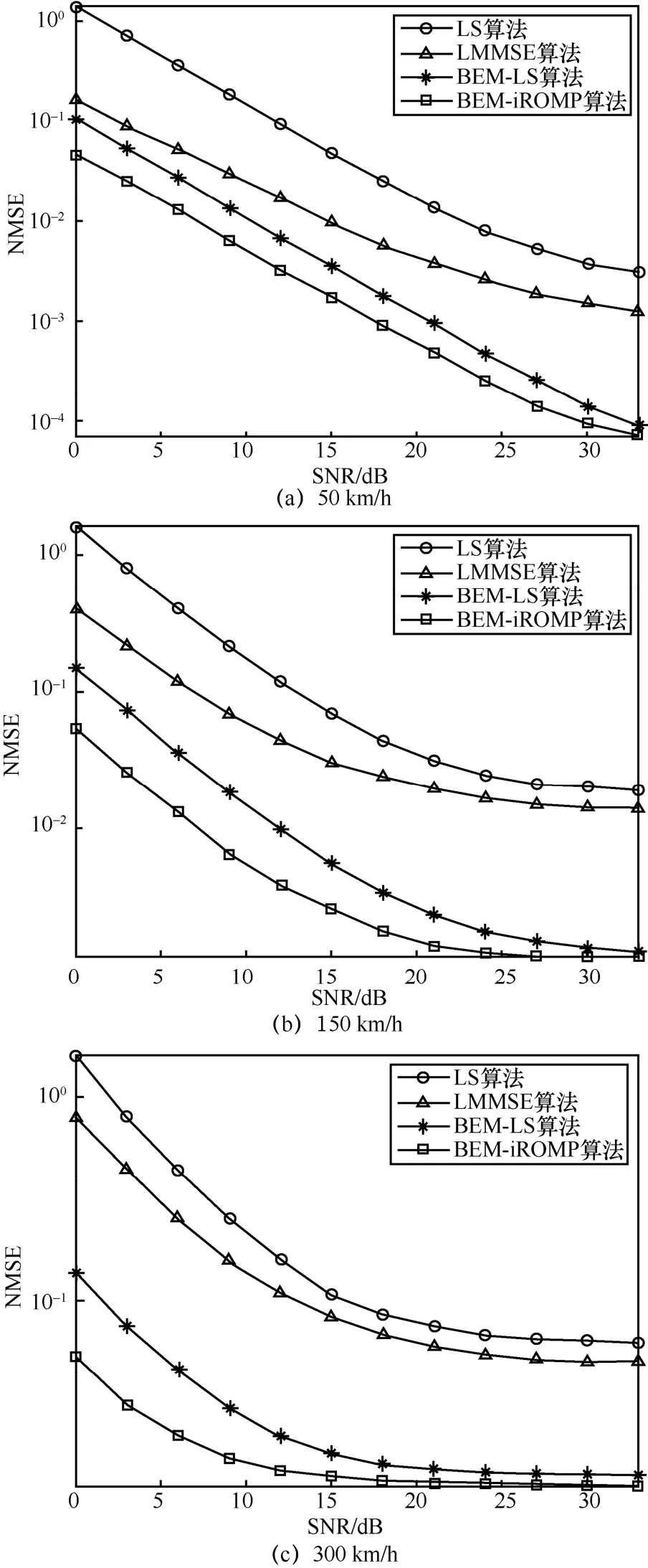
其中，T为采样时间，αs、τs、fs分别为发射天线与接收天线间第s条传播路径的衰落系数、时延和多普勒频移，且s∈[0,S− 1]，S

为了充分利用信道的时频稀疏性，将快时变信道模型建模为BEM，将式(6)转换到时延−多普勒域，获得信道的BEM 函数，即

式(11)保留了Hi的对角线以及对角线两边距离D之间的元素，极大降低了模型的复杂度。

2.2 BEM 稀疏性

如2.1 节所述，采用BEM 可以让信道估计的参数数量大大减少，此外，BEM 系数仍具有稀疏性，本文给出引理与证明。

引理1BEM 函数us[d,l]近似稀疏。

证明对于单抽头s的BEM 函数us[d,l]，虽然大部分能量集中在(fsNT,τs/T)附近，但无法保证us[d,l]是绝对稀疏的。为了验证us[d,l]的稀疏性，需要计算us[d,l]分布在以(fsNT,τs/T)为中心之外的能量分布。

3 稀疏信号重构问题转化

为了便于分析，式(4)的传输模型忽略下标，可转换为

4 基于BEM 的iROMP 迭代稀疏信道估计

为了充分利用基系数的稀疏性，本节提出了BEM-iROMP 算法。其关键处理是，针对式(25)中存在的部分未知元素，采用LS 算法预估计，获取待求解方程，并利用iROMP 对u进行求解，进而通过式(20)求解信道向量h，最后通过迭代不断地利用反馈结果提高信道估计，以获取更高的信道估计精度。具体信号处理过程如算法1所示。

5 算法复杂度分析

不同算法的复杂度对比如表1 所示，主要从算法的乘法运算次数和时间复杂度2 个角度来呈现。

表1 不同算法的复杂度对比

从表1 中可以看出，LS 算法的复杂度最低，为线性阶；复杂度最高的是LMMSE 算法。由于N≫DL，故BEM-LS 算法与BEM-iROMP 算法的复杂度远低于LMMSE 算法。与BEM-LS 算法相比，BEM-iROMP 算法仅多了一个对数阶，即lgT，其原因是BEM-iROMP 算法采用T逼近稀疏度进行重构，增加了复杂度，但是其步长T远小于N，故对复杂度的影响有限。因此，所提BEM-iROMP 算法的复杂度在研究可容忍的范围内。

6 仿真分析

本节仿真的信道模型采用3GPP 协议[15]中定义的扩展车辆（EVA,extended vehicular A）模型，该模型为车联网的开放信道模型。表2 列出了点对点车地通信SC-FDMA 系统仿真参数。

iROMP 算法中，设置步长T=7，M=4，阈值ε1=10−5，ε2=2 ×10−5。为验证高速移动场景下的BEM-iROMP 算法的性能，本节仿真中通过设置不同的车载终端相对移动速度（低速为50 km/h，中速为150 km/h，高速为200 km/h），并与传统的LS 算法、BEM-LS 算法进行对比，仿真指标包括归一化均方误差（NMSE,normalized mean square error）和误码率（BER,bit error ratio）。

表2 系统仿真参数

图1 为理想的基系数u分别在低速、高速情况下的幅值分布。从图1 中可以看出，在低速环境下，除了少数分量的幅值较大外，其余分量的幅值均为0，基系数呈现稀疏的特性；高速环境下的情况类似，且除了幅值较大的分量外，还存在一些幅值在零值附近的、可以忽略的微弱分量，此时基系数呈现近似稀疏的特性。

图1 不同速度下的基系数幅值分布

图2 和图3 对比了LS 算法、LMMSE 算法、BEM-LS 算法以及BEM-iROMP 算法在低速、中速和高速环境下的NMSE 和BER 性能。从图2 和图3中可以看出，在低速环境下，4 种算法的NMSE 和BER 均会随着信噪比（SNR,signal to noise ratio）的增加而迅速减少，这是由于信道冲激响应在一个符号的持续时间内变化不大。其中，LMMSE 算法考虑了噪声的影响，因此性能优于LS 算法，尤其在SNR 条件好的情况下其优势更明显，然而代价是极高的复杂度。BEM-LS 算法和BEM-iROMP 算法的NMSE 性能以及BER 性能显著优于LS 算法和LMMSE 算法，BEM-LS 算法和BEM-iROMP 算法相对于LS 算法和LMMSE 算法，在低信噪比的环境下都有3 dB以上的NMSE增益和1 dB以上的BER增益，在高信噪比的情况下，NMSE 增益达到5 dB以上，BER 增益达到3 dB 以上。其中，BEM-iROMP算法与BEM-LS 算法相比，有3 dB 的NMSE 增益和1 dB 的BER 增益。在中速环境下，LMMSE 算法虽然考虑了噪声的影响，由于高速移动环境下信道冲激响应在一个符号的时间内发生了变化，LMMSE算法和LS 算法都无法捕捉到变化，因此两者的性能差距缩小了。而BEM-LS 算法和BEM-iROMP 算法采用了基扩展模型，能够捕捉到变化，故两者的性能皆优于LS 算法和LMMSE 算法。BEM-iROMP 算法与BEM-LS 算法相比进一步拉开了性能差距，其NMSE 增益达到5 dB，BER 增益达到2 dB。在高速环境下，LMMSE 算法对LS 算法的优势进一步缩小，LMMSE 算法优势不大且复杂度高。而BEM-iROMP算法相对BEM-LS 能够继续保持优势，依然保持5 dB的NMSE 增益以及2 dB 的BER 增益。随着SNR 的提高，BEM-iROMP 算法与BEM-LS 算法基本达到了下限，但BEM-iROMP 算法的下限仍然优于BEM-LS算法。

图4 和图5 对比了4 种算法在不同速度以及不同SNR 情况下的NMSE 性能和BER 性能。从图4和图5 中可以看出，4 种算法的NMSE 和BER 性能都随着速度的增加而下降。即便如此，BEM-LS算法与BEM-iROMP 算法表现出了远低于LS 算法和LMMSE 算法下限的优异性能。对比BEM-LS 算法与BEM-iROMP 算法可以发现，在任何情况下，BEM-iROMP 算法的NMSE 性能与BER 性能均优于BEM-LS 算法，这是由于BEM-LS 算法采用求伪逆矩阵的方式估计基系数，而BEM-iROMP 算法通过少量迭代、跟踪基矩阵中与基系数相关最大的向量来表示基系数，受噪声的影响程度弱于BEM-LS算法，从而更有效、准确地估计出基系数，且付出的复杂度代价较低，具有较强的稳健性。

图2 各信道估计算法NMSE 性能对比

7 结束语

本文围绕V2X快时变场景下的SC-FDMA系统信道估计展开研究，首先根据高速移动信道的稀疏特性，建立了BEM；其次基于所构建BEM，进一步挖掘BEM 系数的稀疏性，将信道估计问题转化为BEM系数稀疏信号重构问题，并提出稀疏信道估计算法BEM-iROMP 算法。仿真结果表明，相对于LS 算法、LMMSE 算法以及 BEM-LS 算法，本文所提BEM-iROMP 算法能够在快时变SC-FDMA 系统中更准确、有效地估计基系数，且具有更强的稳健性。