“轨道板-CA砂浆-支承层”复合模型(TCC)试件累积损伤特性研究
2021-05-13徐桂弘汪权明张志俊吴安杰
徐桂弘,任 旭,汪权明,张志俊,吴安杰
(贵州理工学院,贵州 贵阳 550003)
CRTSⅡ型板式轨道是我国具有自主知识产权的CRTS(China Railway Track System)系列无砟轨道之一。目前,CRTSⅡ型板式轨道已广泛应用于京津城际、沪杭、京沪、宁杭、杭甬、合蚌、京石、石武、津秦、杭长合福等10余条高速铁路或客运专线上,铺设里程双线近5 000 km,是速度350 km/h的高速铁路中铺设长度最多的一种无砟轨道结构型式。

图1 CRTSⅡ型板式无砟轨道结构(单位:mm)
通过项目组员现场调研发现,层与层之间的破坏是CRTSⅡ型板式无砟轨道结构性能劣化的常见现象。无砟轨道结构组成特殊(竖向多层、纵向跨越空间广)、结构材料成分复杂(钢轨、轨道板、水泥乳化沥青砂浆充填层)、荷载作用引起的结构的内力复杂、环境条件复杂等,一旦结构的某个薄弱部位出现微裂纹或伤损后,在温度、水等环境因素和列车疲劳载荷耦合重复作用下,结构内部的材料微结构会继续劣化[1]。长此以往,必然进一步恶化高速铁路线型结构与基础结构服役状态,严重时可能危及行车安全。目前国内外对CRTSⅡ型板式无砟轨道结构层间脱连伤损问题缺乏系统研究。
根据已有的文献资料,涉及无砟轨道伤损研究方面的国家有日本、德国和中国。日本Takahashi等[2]对无砟轨道结构进行调研,发现了CA砂浆出现了伤损,并对轨道板材料受力性能进行了研究。德国早在2004年就关注过无砟轨道结构损伤的情况,曾对汉诺威-柏林高速铁路GETRAC型无砟轨道材料进行了测试,但没有发现明显的内部伤损现象。在国内,朱胜阳等[3]对CA砂浆的伤损问题进行了大量的试验和理论研究,提出CA砂浆材料的统计损伤本构模型和损伤发展动态演变行为。徐桂弘[4]通过缩小的比例模型对无砟轨道裂纹内的水压力进行了试验和理论研究,分析了疲劳荷载作用下裂纹的伤损发展特性。文献[5-6]提出了内聚力模型,并利用该模型模拟了温度和列车动载荷耦合作用条件下轨道板与CA砂浆界面剥离和破碎行为,初步分析了无砟轨道界面损伤的发生机理与发展过程。徐浩[7]对CA砂浆的动态力学性能进行了理论和试验研究。田冬梅[8]通过试验和理论对比分析的方法,研究了水泥乳化沥青砂浆劣化与失效机理。
针对混凝土材料和砂浆材料疲劳伤损累积研究,国内外学者进行了大量的试验和理论分析。自1945年Miner[9]提出了著名的Palmgren-Miner线性疲劳累积损伤理论,针对其不足,国内外许多学者开展了大量的研究。常佳伟[10]对C(素混凝土)、PFRC(聚丙烯纤维混凝土)、SFRC(钢纤维混凝土)、HFRC(混杂纤维混凝土)四种材料进行弯曲疲劳试验,获得了材料在不同应力水平下的疲劳寿命和应变-疲劳寿命曲线。王青等[11]通过对混凝土材料疲劳刚度、强度退化和疲劳残余变形累积发展规律进行分析研究,提出钢筋混凝土构件疲劳性能的等效静力分析方法。吕雁[12]通过四种玻璃纤维混凝土(GFRC)试件的静载试验和等幅循环荷载试验,提出了GFRC弯曲疲劳破坏准则的应变衡量和弹模衡量方法,研究了GFRC的疲劳损伤累积规律,得到了相应的损伤累积方程。Sauedo等[13]采用三参数威布尔累积分布函数拟合相关试验数据,分析了频率和应力比对混凝土疲劳寿命的影响。Bhalerao等[14]提出了一个概率多参数方法,估算疲劳裂纹扩展引起材料失效概率,建立了多参数疲劳裂纹扩展表达式。Guo等[15]采用DSCM(Digital Speckle Correlation Method)方法,通过混凝土结构变形前后散斑图,从纵向和横向位移出发,推导裂纹区域的全场和局部应变场,精确地预测潜在疲劳裂纹起始点。MD NOR N等[16]采用声发射(Ae)技术对RC梁疲劳损伤进行诊断分析。Zanuy等[17]通过混凝土结构中心和偏心压力条件下的截面应力的理论与试验对比分析,提出了一种新的模型研究混凝土结构的疲劳行为。Thomas等[18]、Xiao等[19]研究了不同配比条件下再生混凝土的疲劳强度变化。Gao等[20]利用数字图像相关(DIC)技术对冷再生(CR)混合物疲劳行为进行评价。杨润年等[21]、Chen等[22]对钢纤维混凝土的疲劳损伤问题进行了研究。给出了对应于不同应力水平0.9、0.85、0.8的各种关系曲线。洪锦祥等[23]采用快冻法将混凝土盐冻或水冻至不同损伤程度后进行弯曲疲劳试验,从损伤的角度分析冻融循环作用对混凝土疲劳寿命的影响,建立冻融损伤混凝土的疲劳方程。综上所述,学者基于不同理论方法建立了较多的理论计算模型,然而这些模型都只是针对混凝土材料,对于复合材料、层状材料的伤损特性尚缺乏可参考的资料。
本文针对CRTSⅡ型高速铁路层状复合结构的疲劳伤损现象,浇筑CA砂浆-混凝土复合模型试件(100 mm×100 mm×400 mm),采用MTS试验机施加疲劳荷载,基于连续介质损伤的研究,研究复合模型试件的应力-应变关系特性,研究TCC试件的累积损伤特性及累积损伤演化过程。
1 TCC试件弯曲疲劳试验概况
1.1 试件制备
“轨道板-CA砂浆-底座复合模型”(TCC)试件的基本结构组成见图2。由于GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法标准》[24],并未对混凝土弯曲疲劳试件的规格做相关的规定,本文中参考了JTG E30—2005)《公路工程水泥及水泥混凝土试验规程》[25]、MTS试验机的夹具规格,将TCC试件的规格定为:400 mm×100 mm×100 mm。

图2 TCC复合模型试件(单位:mm)
试件由贵州兴达兴建材公司材料试验室浇筑成形,共20个。混凝土的强度等级为C40,CRTSⅡ型水泥乳化沥青砂浆的配合参照高速铁路CA砂浆配合比。
1.2 试验装置和加载参数
静载与疲劳试验的加载如图3所示,采用4点弯曲的简支加载,在试件的上跨距段(纯弯段)获得近似纯弯曲的应力状态,试验支座为一端滚动一遍滑动,下跨距为300 mm,上跨距(加载间距)100 mm,纯弯曲段布置在左右1/3跨处。
TCC弯曲疲劳试验条件同静载弯曲在50 KN/MTS疲劳试验机上进行,静载弯曲试验和疲劳弯曲试验均采用应力控制,速度为0.05 kN/s,加载频率为20 Hz无间歇的正弦波。MTS试验机自带位移传感器可以记录疲劳加载幅值、跨中位移、循环周次等相关参量,并可以实时在计算机屏幕上显示,当试件断裂或循环周次达到2×106次,程序可自动停止数据采集。

图3 试验装置及试验设备
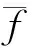
2 静载试验结果
通过对6个试件静态力学性能的试验,测定复合试件的弯曲强度,试验结果见表1。

表1 静态弯曲试验结果
由表1可知,4号试件跨中最大,为1.03 mm,极限弯曲荷载为10.364 3 kN,2号试件的轴向极限荷载最大,为19.666 3 kN,跨中最大挠度0.935 2 mm。由于2号试件的的试验结果与其他结果偏差大,去除2号试件,取其余试件弯曲极限荷载的平均值,得到静载弯曲的平均值为fmax=9.61 kN。
3 试验结果及分析
3.1 疲劳寿命和弯曲疲劳回归方程
TCC复合试件在不同应力水平下的疲劳寿命试验结果,见表2。

表2 弯曲疲劳试验结果
由表2可知,随着应力水平的增加疲劳寿命逐渐降低。当应力水平小于0.72时,TCC复合模型试件超越200万次的疲劳的概率为95%,随着应力水平的增加,复合模型试件超越200万次的概率大大降低。用最小二乘法对试验结果进行线性回归得到TCC试件的S-N曲线和拟合方程为
Smax=2-0.199 5logNf
(1)
式中:Smax为应力水平;Nf为疲劳寿命。
3.2 复合模型试件的弯曲疲劳破坏特性
为研究“轨道板-CA砂浆-支承层”复合模型(TCC)试件在弯曲疲劳荷载作用下破坏特性,采用电子显微镜对TCC试件破坏全过程进行观察,得到TCC试件的裂纹扩展与循环周次的变化关系见图4。

图4 疲劳荷载作用下TCC裂纹扩展情况(S=0.59,TCC-1)
由图4可知,与普通混凝土疲劳破坏时试件底部有较多的细小裂纹不同,TCC试件在疲劳破坏时只出现一条主裂纹,试件从主裂纹处完整的断开,见图4(b)。主裂纹在循环次数为1 200次是就已经出现(见图4(a)),但是裂纹的扩展速度很慢。这一现象主要是由于CA砂浆层具有较高的弹性,提升了材料基体和复合式结构模型的抗裂性能和变形能力。
TCC试件破坏,正如工程现场所调研的那样,在层与层之间的黏结处,出现了水平的裂纹。随着疲劳次数的增加,水平裂纹扩展一段后,在最上层混凝土的初始缺陷或材料结构的薄弱部位,出现竖向裂纹。TCC试件内部区域微裂纹一步连通,从而导致试件最终疲劳破坏。弯曲疲劳试件的试验中,绝大多数的试件都出现这种断裂的特性。可见,层与层之间的黏结,仍然是TCC试件的强度和稳定的薄弱部位。这与工程现场调研结果一致。
3.3 疲劳荷载作用下试件的变形特性
为观察TCC复合模型试件的从加载到破坏全过程的荷载-变形曲线,试验加载应力水平S=0.72时,得到TCC模型试件从开始加载到试件破坏的全过程“荷载-变形曲线”,见图5(a),该试件破坏时的循环周次为3.58×106。为了与普通混凝土试件的变形破坏进行对比,制作了与TCC试件大小相一致的混凝土试件(C40),其“荷载-变形曲线”见图5(b)。
据文献[26]混凝土试件疲劳荷载作用下,其破坏基本呈三个阶段,见图5。并与普通混凝土对比发现:随着循环次数的增加,TCC模型试件的“循环荷载-位移曲线”呈现由疏到密的发展规律(普通混凝土的曲线密集),且曲线不断向右侧移动,疲劳变形发展明显的呈现四个阶段规律:

图5 荷载位移关系曲线TCC和普通混凝土
第Ⅰ阶段为荷载稳定阶段。MTS疲劳试验机应力加载水平为逐步加载,在加载前期,夹具与试件的接触为点接触,当荷载达到6.92 kN时,夹具与试件的接触逐步成为局部面积接触,因此出现轴向位移突然增加的现象。此阶段普通混凝土也会出现。
第Ⅱ阶段为CA砂浆压密阶段。表现为荷载-位移曲线稀疏大,实质是CA砂浆密度增加,孔隙、孔洞被压密。该阶段,微裂纹、孔隙等压密量大于扩展量,但不可避免的在某些部位出现新的微裂纹。混凝土的疲劳变形曲线不存在该阶段。
第Ⅲ阶段为混凝土压密阶段:混凝土内部的空隙、空洞被压密。混凝土与CA砂浆之间的残余变形也在不断的增加,从而引起复合模型试件的整体抗弯刚度随着荷载循环次数的增加而退化,试件的轴向位移不断增大。
第Ⅳ阶段:随着疲劳循环次数的增加,混凝土及CA砂浆的内部损伤不断累积,宏观上表现为载荷-挠度曲线呈非线性变化,并产生残余变形继续增大。裂纹迅速扩展、贯通,混凝土材料失稳破坏。混凝土宏观荷载-变形曲线受个别裂纹演化控制,主要体现结构效应,已不属于单纯的材料性质。
3.4 复合模型试件疲劳累积损伤演化
3.4.1 弯曲疲劳动模量分析
TCC复合模型试件的弯曲疲劳动弹性模量是研究TCC试件刚度衰减及伤损演化的重要参量。通过MTS疲劳试验机进行的4点弯曲试验,得到的一般是荷载-挠度曲线,由材料力学公式转化,TCC试件的动弹性模量为
(2)
式中:Ef为弯曲疲劳动弹性模量;σ为应力;δ为应变;P为疲劳荷载,kN;l为试件的下跨距;h为试件截面高度;I为试件截面的惯性矩;f为试验测量得到的试件跨中挠度。依据式(1)可根据不同循环周次时疲劳试验结果f,求解该周次对应的动弹性模量,该模量为一个变化值,又称动弹性模量。
3.4.2 弯曲疲劳应变特性
通过试验结果整理分析,可得到不同应力水平条件(S不同)下正则化疲劳变形(δ=εn/εmax)随循环比(即循环次数与循环寿命之比,为n/N)的变化曲线,即疲劳应变演化曲线。其中εn为循环周次为n时疲劳变形,εmax为试件断裂时最大疲劳变形。
当S=0.75、S=0.85、S=0.95时疲劳应变演化曲线,见图6。其中,Δδ20和Δδ83分别为循环次数与疲劳寿命比为20%和83%时的疲劳总应变。
由图6可知,“混凝土-CA砂浆复合模型试件”在弯曲疲劳荷载作用下,疲劳应变演化的曲线大致呈S形状,曲线大致可分为三个阶段,第1阶段,疲劳应迅速增大,该阶段占疲劳寿命的10%~20%;第2阶段,为疲劳应变稳定增长阶段,该阶段疲劳循环次数总疲劳寿命的60%~70%,第3阶段,轴向位移突然增大,直到试件断裂,该阶段占疲劳寿命的10%~20%。
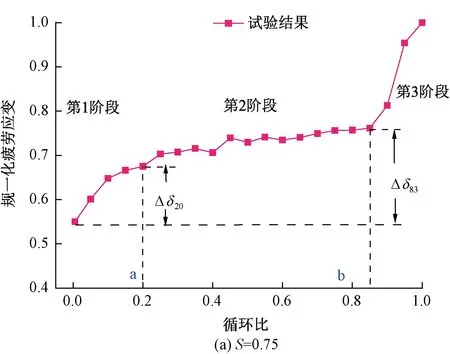
图6 弯曲疲劳变形试验曲线和拟合曲线
由图6的对比可知,随着应力水平的提高会导致试件变形增长速率趋于平缓,但是初始疲劳应变增加,即TCC的初始应变和应力水平S成正比。
3.4.3 疲劳累积损伤的演化方程
通过本批试件的弯曲疲劳试验,观察到TCC试件疲劳损伤累积过程是非线性的过程,疲劳应变演化曲线呈S形发展,并且在总应变发展的第2阶段具有恒定应变率,且第2阶段的应变率与疲劳荷载的性质有关,见图7。

图7 复合模型疲劳应变发展规律
疲劳应变的第2阶段占总疲劳寿命的80%以上,对疲劳寿命起决定性影响,甚至有文献直接把应变的第2阶段作为结构的整个疲劳寿命[26-27]。
假设第1阶与第3阶段疲劳应变呈线性关系。通过对试验结果分析,第二阶段的取值定为20%~82%,如图7所示,该阶段的疲劳应变与疲劳寿命的关系为
lgNf=β1+β2lgδLI
(3)
式中:Nf为疲劳寿命;β1、β2为材料常数,通过弯曲疲劳试验测得;δLI为试件的疲劳应变。
假设疲劳开始时的初始应变为δ0,也就是本文前面所提到的荷载稳定阶段结束时所对应的应变。第一阶段的应变为Δδ20。并利用材料力学基本公式和式(2)可得到疲劳总应变为
(4)

δ82=Δδ20+0.62δLI,为循环次数与疲劳寿命比为82%时的疲劳总应变。由图7中第2阶段应变发展规律计算得到。
计算得到的疲劳应变通过破坏准则与本构关系相联系,因此疲劳累积损伤标量Dfat为
(5)
式中:Dfat为疲劳累积损伤标量;Ef为混凝土疲劳破坏时弹性模量;δf为试件破坏时应变;E0为初始弹性模量。
4 结论
(1)TCC试件的破坏与普通混凝土试件的破坏有显著的不同。TCC试件在疲劳破坏时只出现一条主裂纹,试件被主裂纹隔断,但在层间粘结处,出现了水平的裂纹。CA砂浆具有较高的弹性,在弯曲疲劳中起到了一定的阻裂作用。
(2)TCC模型试件的“循环荷载-位移曲线”呈现由疏到密的四阶段发展特性:荷载稳定阶段、CA砂浆的压密阶段、混凝土压密阶段、破坏阶段。而普通混凝土的变形曲线只有三个阶段。
(3)疲劳应变呈倒S型三阶段变化特性。第1阶段,疲劳应迅速增大,该阶段占疲劳寿命的10%~20%;第2阶段,为疲劳应变稳定增长阶段,该阶段疲劳循环次数总疲劳寿命的60%~70%,第3阶段,轴向位移突然增大,直到试件断裂,该阶段占疲劳寿命的10%~20%。
通过假设第1阶与第3阶段疲劳应变与循环荷载线性关系,结合动弹性模量的计算公式及疲劳寿命的线性回归方程,提出了TCC试件的疲劳累积损伤演化方程。
