基于可线性化Wiener过程的牵引供电设备状态检修决策研究
2021-05-13范瑞栋
林 圣,李 楠,杨 超,范瑞栋
(1.西南交通大学 电气工程学院,四川 成都 611756;2.国家电网内江供电公司,四川 内江 641100;3.中铁第一勘察设计院集团有限公司,陕西 西安 710043)
牵引供电设备的可靠运行需要检修维护工作的有效开展。当前,定期维修模式仍是我国牵引供电设备的主要检修维护手段。该模式存在维修频繁和效率低下的问题,导致设备运行费用高昂[1]。基于检测结果的状态检修可以较好地消除日常定期维修的缺点,已经引起了许多科研工作者和运维单位的关注[2-3]。
围绕设备状态检修决策,文献[4-7]以可靠性、经济性以及运行条件等因素为约束条件或决策目标已做了大量工作。文献[5-6]基于可靠性分析建立检修决策模型,以降低期望检修费用率为目标,实现最优检测周期决策。在此基础上,文献[7]针对GIS设备易受剧烈负荷冲击的情况,基于Gamma过程与复合泊松过程的竞争性失效模型,完成了冲击维修阈值与检测周期的最佳组合,旨在实现最高的检修性价比。
然而,上述研究都是在匀速劣化失效模型或匀速劣化失效与冲击失效组成的竞争失效模型基础上展开的;实际上设备性能劣化将随时间逐步加速[8-10]。同时,现有研究基本将维修效果设置为修复如新,即完美维修;而实际维修操作基本都是不完美维修[11]。基于此,文献[12]利用两阶段Wiener过程建立设备的劣化模型,通过两个参数不同的传统Wiener过程描述设备正常状态与有缺陷状态的劣化过程,在正常状态和有缺陷状态设备分别按不同的速度匀速劣化,设备正常状态和有缺陷状态间有明显转折点。文献[13]将预防性维修考虑为不完美维修,并以期望运行费用率最低为目标进行最优检修决策,但未考虑设备失效后修复性维修的不完美性。综上所述,现有研究在设备劣化速度和不完美维修方面的综合考虑尚不完善,有必要进行更加深入的研究。
为此,本文同时考虑牵引供电设备性能劣化非均匀性与维修效果不完美的特点,提出一种新的检修决策方法。利用Wiener过程的特征描述设备劣化过程逐步加速的过程,使用正态分布刻画预防性维修以及修复性维修都是不完美维修的特点,根据劣化模型分别推导预防性维修和修复性维修实施的概率,进而得到设备运行费用率的期望值,并以实现最低的运行费用率为目标,求解最优的检测周期和预防性维修阈值。最后,通过算例分析验证了方法的有效性。
1 牵引供电设备劣化模型
1.1 设备性能劣化过程分析
设备性能劣化主要是因为老化和磨损[14]。除此之外,一些外部因素也会影响设备劣化过程,如环境湿度、负载变化以及人为干扰等[15]。内外因素的共同作用使牵引供电设备性能演变过程随运行时间的增加呈现出如下特点:
(1)短时间尺度上,随着设备外部运行条件的变化,设备劣化出现非单调变化[16]。
(2)长时间尺度上,随着设备运行时间的增加,设备劣化主要为加速劣化。
设备劣化值下降到某种程度将会导致设备故障,劣化值越大,设备故障的可能性也越大。因此,在设备群中设备故障可能性越大,故障累计数量也就越多。统计某地区从2006年3月24日到2014年9月16日的483个同类牵引供电设备的故障次数,可以得到设备群总故障次数的变化规律,如图1所示。

图1 设备群总故障次数及变化规律
由图1可知设备群故障次数的变化特点如下:
(1)短时间尺度上,设备群在一定时间段内的故障数量可以比前后相同时间段更多或更少,这表明设备的劣化出现非单调变化。
(2)长时间尺度上,随着设备运行时间的增加,设备群中的故障数量会缓慢加速变大,这表明设备的劣化趋于加速。
1.2 劣化过程数学模型
可线性化Wiener过程[17-18]通过对传统Wiener过程的改良,不仅可以表征短时间尺度上的非单调特性,还可以表征长时间尺度上的逐步加速特性。因此本文使用可线性化Wiener过程来建立描述设备劣化的数学模型。
根据劣化值Xd(t)刻画设备在t时刻的劣化状态,该值基于可线性化Wiener过程建模可表示为
Xd(t)=μ·tγ+σ·B(tγ)t≥0
(1)
式中:{B(tγ),t≥0}为tγ的标准Wiener过程,其中,γ为不小于1的修正参数;μ、σ分别为漂移参数、扩散参数。由Wiener过程特征:Xd(t)是均值为μtγ方差为σ2tγ的正态分布,由参考文献[17]中的极大似然估计法得到μ和σ的值。

(2)
式中:Φ(·)为标准正态分布。
参考文献[7]中对可靠度的定义,在设备能够正常工作的范围内,Xd(t)不大于失效阈值L的概率即为设备在t时刻的可靠度,根据式(2)可靠度R(t)可以表示为
(3)
1.3 维修后劣化模型
在进行维修后设备的性能将会提高,处于“恢复如新”和“恢复如旧”之间。设备维修后的状态决定其可以继续可靠运行的时长,而其可靠运行时长又决定了在总的服役时间内需要维修的次数,推广到同类设备群时,设备维修后的状态分布特征可以利用同类设备群维修次数的分布特征描述。统计图1中从2006年3月24日到2014年9月16日这段时期内的483个同类牵引供电设备的维修次数(包括定期预防性维修和故障后修复性维修),采用极大似然估计法拟合统计数据,可以得到设备维修次数的分布特征,如图2所示。
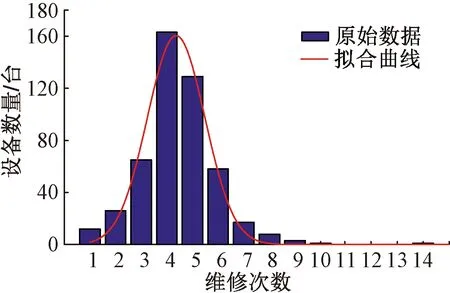
图2 设备维修次数统计及分布规律
由设备维修次数分布规律可知,在同类设备群中维修次数符合正态分布。因此,可以使用正态分布来建模牵引供电设备维修后状态的分布特征[19],并且维修后设备性能状态将恢复为原始设备特征重新变化。同时,随着维修次数的增加设备预防性维修的效果会逐渐下降[11,13]。
1.3.1 预防性维修后劣化模型
在检测设备状态时,如果发现其劣化值大于或等于预防性维修阈值(前提是该设备劣化值小于失效阈值),则应进行预防性维修以改善其状况,如果在t0时刻对设备开展预防性维修,则根据式(1),得到维修后的值Xdp(t)为
Xdp(t)=Xp(t0)+μ·(t-t0)γ+σ·B((t-t0)γ)
t≥t0
(4)
式中:Xp(t0)为实施预防性维修后设备性能改善后的劣化值,且Xp(t0)~N(kμ1,kσ12),μ1为首次预防性维修后劣化值的期望;σ1为对应的标准差,其值可以参考文献[20]中的方法进行求解,由预防性维修的历史数据估算得到,其中k为已实施的预防性维修次数。
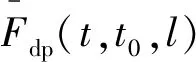
(5)
因此,预防性维修后可靠度函数Rp(t,t0)可表示为
(6)
1.3.2 修复性维修后劣化模型
由于牵引供电设备的逐渐劣化存在随机性,任一运行时刻设备劣化值都存在达到失效阈值进而发生失效的可能。因为设备的失效过程体现了“自明性”[19],失效后需立即对设备进行维修以恢复其正常运行。在维修中,主要方法是替换有故障的部件而不替换未损坏的部件;但实际上没有损坏的部件由于运行了一段时间也存在部分劣化,导致修复性维修是一项不完美的维修模式。修复性维修如果在t0时刻实施,根据式(1)修复性维修后设备的劣化值Xdc(t)为
Xdc(t)=Xc(t0)+μ·(t-t0)γ+σ·B((t-t0)γ)
t≥t0
(7)
式中:Xc(t0)为修复性维修后设备性能恢复后的劣化值,且Xc(t0)~N(μ2,σ22),μ2为修复性维修后劣化值的期望,σ2为对应的标准差,可以参考文献[20]中的方法进行求解。
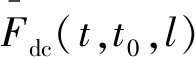
(8)
因此,修复性维修后设备可靠度函数Rc(t,t0)可表示为
(9)
2 基于可线性化Wiener过程的检修模型
2.1 预防性维修模型建立
在设备服役时期,按照恒定周期T开展检测工作获取设备性能信息,若在检测时刻得到劣化值大于预防性维修阈值Lp,同时在失效阈值L以下,则对设备实行预防性维修。在执行实际的维修活动时,维修时间(取为1 d)比设备运行时间(取为1 a)要短得多,因此本文没有考虑维修花费的时间。在第j(j=1,2,…)次检测中,也就是jT时刻是否实施预防性维修可分3种情形,如图3所示。
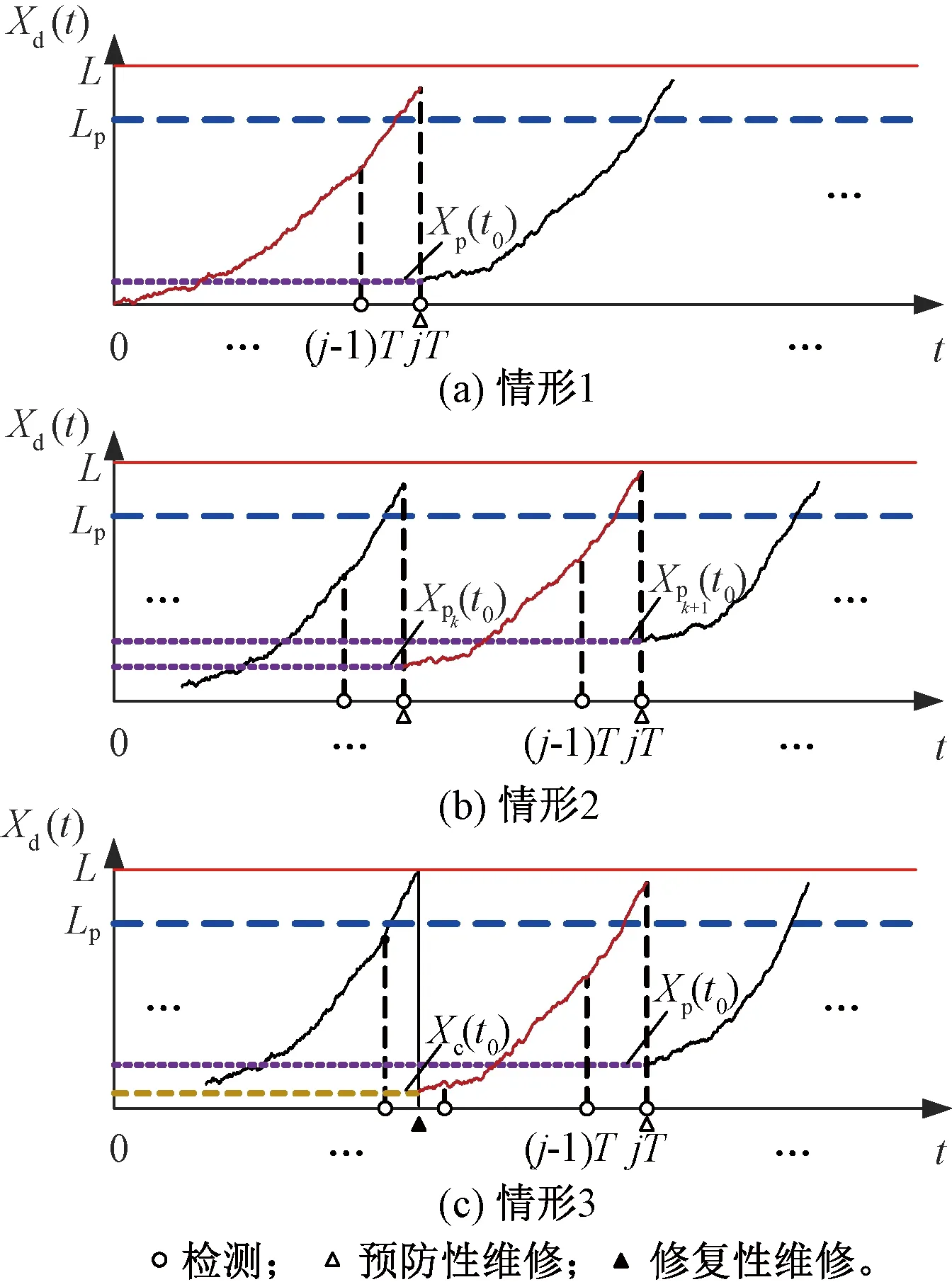
图3 设备jT检测时刻进行预防性维修
(1)情形1:在jT时刻以前,设备从未开展过任何维修,即设备处于全新状态,劣化值从0开始增大。
(2)情形2:在jT时刻以前,上一次维修为预防性维修,劣化值从预防性维修后性能改善后的值Xp(t0)开始增大。
(3)情形3:在jT时刻以前,上一次维修为修复性维修,劣化值从修复性维修后性能恢复后的值Xc(t0)开始增大。
若设备劣化值在(j-1)T时刻小于Lp,且在jT时刻大于等于Lp但小于L时,则在jT时刻对设备进行预防性维修。
由式(2),设备劣化值在(j-1)T时刻小于预防性维修阈值Lp的概率可以表示为
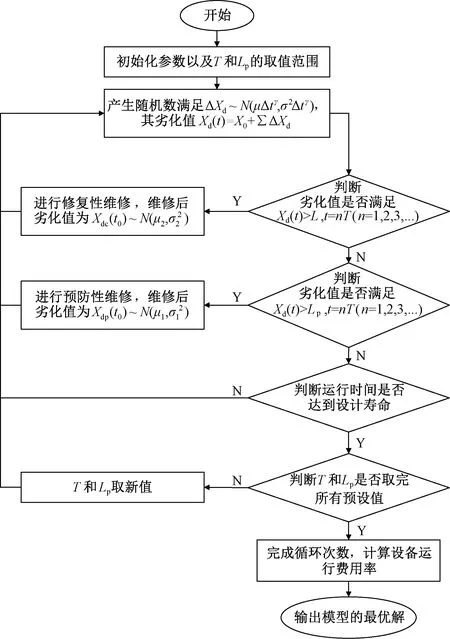
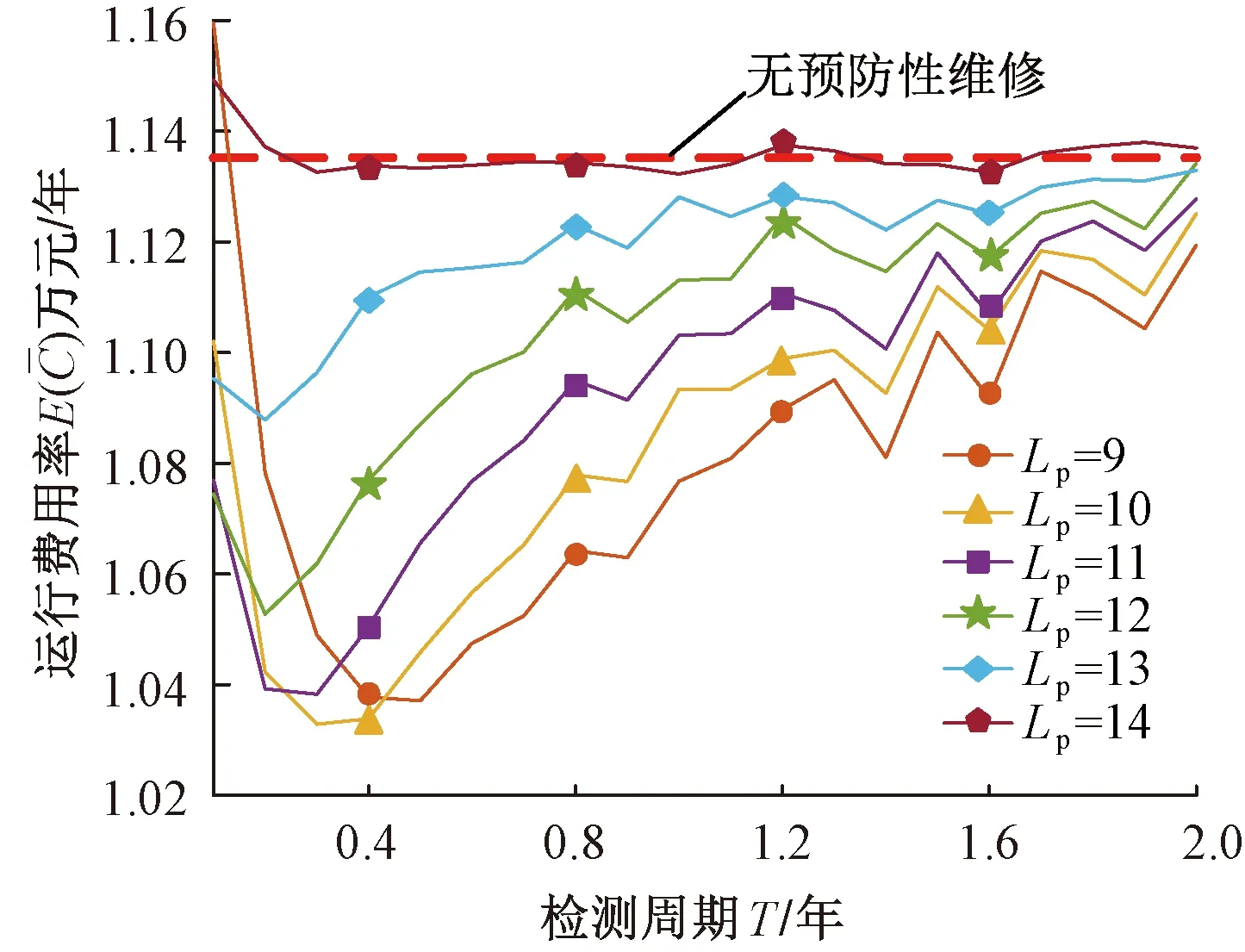
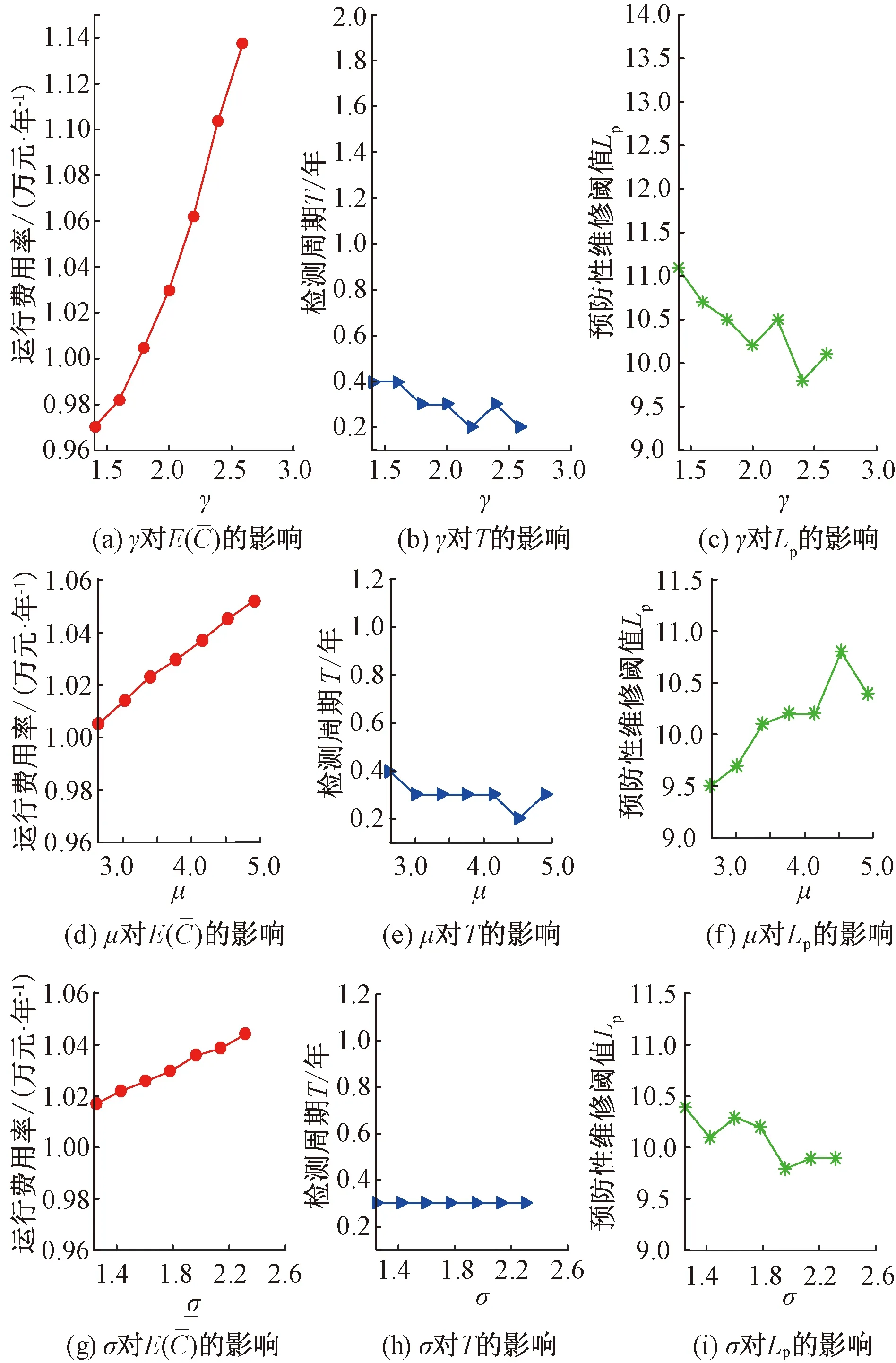
P1=Pr{Xd((j-1)T) (10) 同理,在jT时刻设备性能劣化值大于等于预防性维修阈值Lp,同时小于失效阈值L的概率可以表示为 P2=Pr{Lp≤Xd(jT) (11) 根据式(10)和式(11),对图3(a)所示的第1种情形,预防性维修发生在设备运行到jT时刻的概率Ppm1可表示为 Ppm1(j,T)=Pr{Xd((j-1)T) (12) 同理,对图3(b)所示的第2种情形,预防性维修发生在设备运行到jT时刻的概率Ppm2可表示为 Ppm2(j,T)= Pr{Xdp((j-1)T) (13) 同理,对图3(c)所示的第3种情形,预防性维修发生在设备运行到jT时刻的概率Ppm3可表示为 Ppm3(j,T)= Pr{Xdc((j-1)T) (14) 同预防性维修,设备在[(j-1)T,jT)时段内是否实施修复性维修可分为3种情形,如图4所示。 图4 设备[(j-1)T,jT)时段进行修复性维修 若设备在运行到(j-1)T时刻其性能劣化值均小于预防性维修阈值Lp,但在Ts时刻(Ts∈[(j-1)T,jT))其性能劣化值达到失效阈值L,那么设备在Ts时刻需实施修复性维修以恢复其正常运行。 根据式(2)可知,设备劣化值在Ts时刻的劣化值达到失效阈值L的概率可以表示为 P3=Pr{(j-1)T≤Ts (15) 根据式(10)和式(15),对图4(a)所示的第1种情形,修复性维修发生在设备运行到[(j-1)T,jT)时段内的概率Pcm1可表示为 Pcm1(j,T)= Pr{Xd((j-1)T) (16) 同理,对图4(b)所示的第2种情形,修复性维修发生在设备运行到[(j-1)T,jT)时段内的概率Pcm2可表示为 Pcm2(j,T)= Pr{Xdp((j-1)T) fdp(t|(j-1)T,nT,L-l)]dldt (17) 同理,对图4(c)所示的第3种情形,修复性维修发生在设备运行到[(j-1)T,jT)时段内的概率Pcm3可表示为 Pcm3(j,T)= Pr{Xdc((j-1)T) fdc(t|(j-1)T,nT-z,L-l)]dldtdz (18) 本文以实现设备运行费用率最低为决策目标,同时保证设备的可靠运行(即设备劣化值不超过L)。 s.t.Xd(t) (19) 设备全寿命周期内运行费用率期望可表示为 (20) 式中:Tlife和Ctotal分别代表牵引供电设备的设计寿命和全寿命周期的总费用,具体包含设备采购、检测、预防性、修复性维修和失效风险等费用。 E(Ctotal)=cpm·E(Npm)+ccm·E(Ncm)+ cr·E(Nr)·pr+ci·Ni+Cc (21) 式中:cpm为一次预防性维修成本;Npm为全寿命周期中预防性维修数量的总和;ccm为一次修复性维修成本;Ncm为全寿命周期中修复性维修数量的总和;cr为失效一次的成本;Nr为全寿命周期中失效数量的总和;pr为备用设备不能正常投入工作的概率;ci为一次检测的成本;Ni为全寿命周期中检测数量的总和;Cc为设备采购成本。 在设备运行过程中,按恒定时间T检测设备实际劣化值,全寿命周期内的检测次数可表示为 (22) 根据式(12)~式(14),设备全寿命周期内预防性维修次数的期望可表示为 E(Npm)= (23) 根据式(16)~式(18),设备全寿命周期内修复性维修次数的期望可表示为 E(Ncm)= (24) 设备失效不能正常工作的次数是指设备在其整个寿命期间执行的修复性维修次数,因此有 E(Nr)=E(Ncm) (25) 本文的检修决策模型中有两个需要决策的变量,分别为检测周期T和预防性维修阈值Lp。以设备运行费用率最低为决策目标,寻找T和Lp的最优组合得到最优检修方案。由于常规的解析法在本模型中计算量大且困难,因此本文利用Monte Carlo法对上述模型进行仿真求解。求解流程如图5所示。 图5 模型求解流程 变压器是变电站内转换电能的重要设备,是运维公司的重点维护对象。本文以某城轨牵引变电所干式变压器数据为例进行分析。表1为该干式变压器相关数据信息,设劣化过程参数μ=3.78,σ=1.78,维修效果参数μ1=1.64,σ1=0.37,μ2=1.89,σ2=0.57,取γ=2,失效阈值L=15[7],备用设备投入失败概率pr=0.297[21]。 表1 干式变压器相关参数 表2为干式变压器的检修费用统计,其中失效费用假设为cr=20 000元/次。 表2 检修费用统计 利用本文决策模型和相应参数,在Lp取值为9~14时,不同检测周期对应的设备运行费用率和不考虑预防性维修时运行费用率对比如图6所示。 图6 待决策变量取值范围 由图6可知,预防性维修阈值Lp取值从9逐渐增加至14时,设备运行费用率最低值先逐渐变小再逐渐变大,结果显示最佳的预防性维修阈值处于9~14之间。当检测周期T从0.1逐渐增加至2时,设备运行费用率最低值先逐渐变小再逐渐变大,结果显示最佳的检测周期处于0.1~2之间。 因此,预防性维修阈值Lp的取值范围选为9~14,步长选为0.1;检测周期T的取值范围选为0.1~2,步长选为0.1。采用Monte Carlo法按照图5所示步骤求解本文的决策模型。为降低Monte Carlo法求解过程中随机性的影响,仿真次数取为1 000后计算平均值,不同检修组合下的运行费用率如图7所示。 图7 运行费用率仿真结果 图8 最优决策结果 由图8可知,最优决策中设备运行费用率最优值是10 296元/年,相应的最佳检测周期是0.3年,最佳预防性维修阈值是10.2。 通过分析可知,不管是随着T还是Lp的增加,设备运行费用率都呈先减小后增大的变化趋势。原因在于,在T或Lp值过小的时候,进行了过多的预防性维修,造成设备过度维修以至于运行成本变大;在T或Lp值过大的时候,进行的预防性维修太少,造成设备维修不足以至于失效可能性变大,修复性维修和失效风险成本进一步增加了运行成本。因此,本文所提方法可以改善出现维修“过剩”和“不足”的情况。 通过Monte Carlo仿真设备的劣化状态,当T=0.3年,Lp=10.2时,设备在运行期间的劣化值变化过程如图9所示。 由图9可知,随运行时长的增加设备的劣化值也随之加速增加。从图9还可以看出,在2.7、5.4、7.8和10.2年时设备的劣化值均大于预防性维修阈值10.2,此时应对设备开展预防性维修,此外,设备在运行期间未失效。图9表明,设备维修后的性能并没有完全恢复,随着每次维修其性能会逐渐劣化,这说明预防性维修具有不完美维修的特点,同时维修次数的增加还会导致维修质量逐渐下降。 由式(3)、式(6)和式(9)可得到设备在全寿命周期内的可靠度曲线,如图10所示。 图10 设备运行期间可靠度曲线 由图10可知,当检测周期T为0.3,预防性维修阈值Lp为10.2作为检修方案时,在任一检修周期内设备长时保持可靠度为1的状态运行,随运行时间的增加劣化值快速增大,可靠度随之快速由高降低。当设备劣化值超过预防性维修阈值且在检测时刻时,及时的预防性维修措施阻止了设备可靠性降至零。除此之外,可靠度在降至为零前(即劣化值超过失效阈值)采取预防性维修,尽可能地增加了一个检修周期内设备的运行时间,从而减少了设备在整个服役期间的维修次数,又避免了设备失效,这就是本文决策模型的决策结果可以改善传统维修方式维修“过剩”和“不足”的原因。 综上所述,采用本文决策模型得到的最优决策结果作为设备的检修方案时,可以有效避免设备劣化值超过失效阈值,保证了设备运行期间的可靠性。 为验证本文所提方法的有效性,在相同的服役过程检修情况下分析现有检修决策方法。根据传统的Wiener过程建立模型,考虑设备相同的劣化结果和费用,最后得到的最优决策结果见表3。 表3 传统方法最优决策结果 根据表3分析,设置同样的参数时,本文提出的决策方法和传统方法的最佳检测周期相同均为0.3年,但最佳预防性维修阈值变为11.3,相比于本文中的10.2有所提高。在设备的运行成本方面,传统的检修决策最小运行费用率为11 160元/年,高出本文最佳运行费用率8.4%。这是由于传统的检修在推迟设备预防性维修的同时使得失效可能性变大,在设备失效可能性变大后设备损失的费用大于增加运行时间所节省的费用。故本文的方法有效改善了现有的检修策略。 本文建立的劣化模型包含了3个参数,分别为漂移参数μ、扩散参数σ和速度修正参数γ。固定任意2个参数不变,以文中模型参数所取值的1/10为变量,变动余下的第3个参数值,代入决策模型后得到相应的最优决策结果,可以反映出劣化模型参数对最终决策结果的影响,如图11所示。 图11 劣化模型参数对最优决策结果的影响 由图11可知,3个劣化模型参数均会影响决策结果。在固定3个参数相对变化量相同时,模型3个参数对最后结果的影响程度由大到小分别是γ、μ和σ。原因在于,γ造成模型随时间增加成指数变化,其较小的变动即可造成模型较大的变化,对决策结果影响非常显著;μ造成模型随时间增加成线性变化,对模型的影响小于γ,对决策结果的影响较小;σ造成模型分布呈离散变化,对模型的影响均小于γ和μ。 在本文的决策模型中检修费用由三部分组成,分别为检测费用ci、预防性维修费用cpm和修复性维修费用ccm。固定任意2个费用参数不变,同样以文中检修费用参数取值的1/10为变量,变动剩下的第3个参数值,代入决策模型后得到相应的最优决策结果,可以反映出检修费用参数对最终决策结果的影响,如图12所示。 图12 费用参数对最优决策结果的影响 由图12可知,3个检修费用参数均会影响决策结果。在固定3个参数相对变化量相同条件下,检修费用的3个参数对决策结果的影响程度各不相同,影响程度由大到小为cpm、ci和ccm。原因在于本文决策目标是在保证设备可靠运行(劣化值不超过失效阈值)的条件下,使设备运行费用率最小。为了实现上述目标,检修活动只能包含低成本的检测和预防性维修,不能出现昂贵的修复性维修。由于预防性维修成本超过检测成本,故会出现以上影响。 由于同一个牵引所的不同设备其劣化模型参数是不同的,不同地区的牵引供电设备其检修费用参数也是不同的,所以通过参数灵敏度分析可以直观的指导运维人员在建立相关设备检修决策模型时应重点关注模型参数,使得最终的决策结果更符合实际。 本文提出的基于可线性化Wiener过程的状态检修决策方法,不仅考虑了设备加速劣化的特性还考虑了实际维修活动的不完美特点,建立的劣化模型更加符合实际,在此劣化模型基础上推导了状态检修决策方法数学解析表达式,并利用Monte Carlo法求解决策模型最优解。算例证明,该方法能有效避免维修过剩和不足的问题,既降低了运行费用,又保证了设备运行的可靠度,对牵引供电设备的状态检修工作有一定的指导作用。

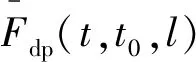
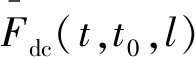
2.2 修复性维修模型建立





3 决策模型与求解
3.1 决策目标模型的建立


3.2 模型求解
4 算例分析


4.1 状态检修决策结果分析

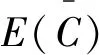
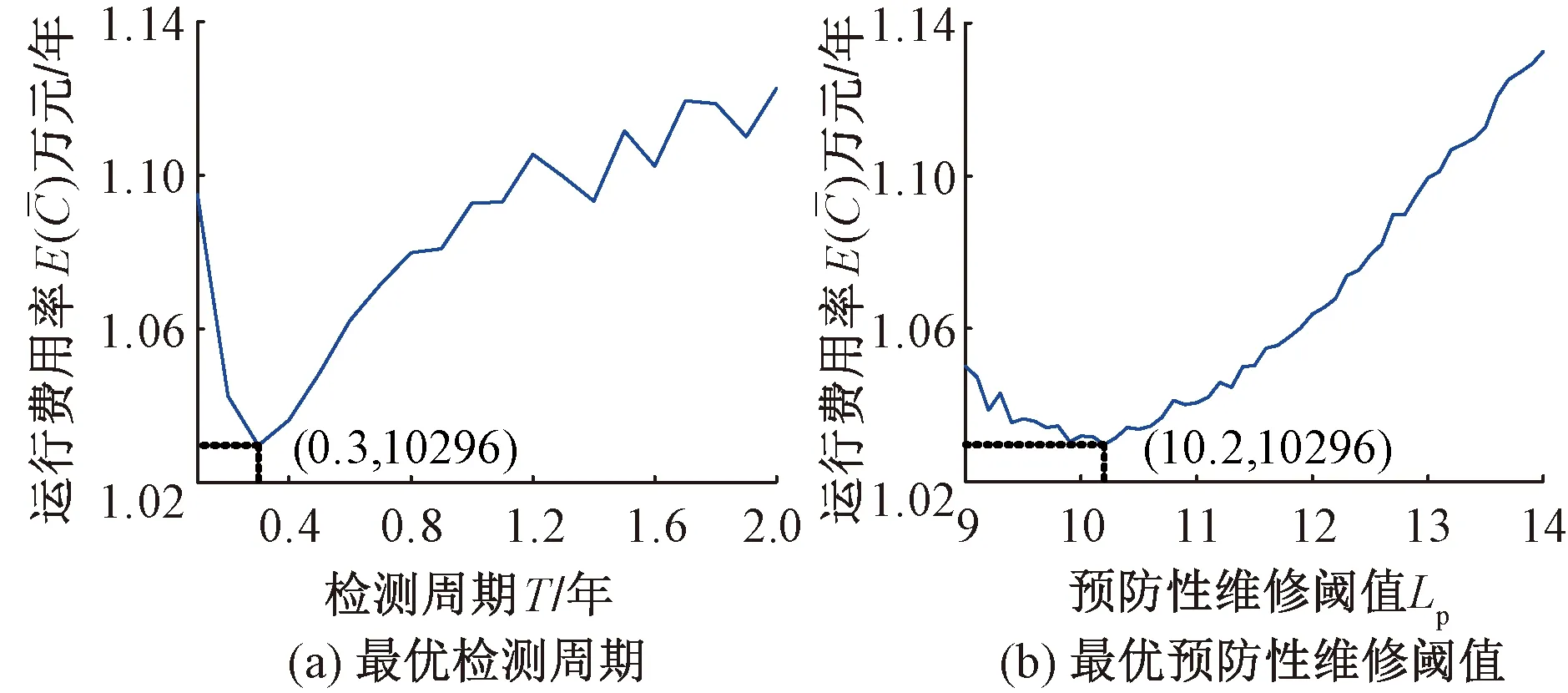
4.2 最优决策结果的可靠度分析

4.3 方法对比

4.4 模型中参数灵敏度分析

5 结束语
