一种基于深度信念网络的径流量预测方法

2021-05-13钱立鹏刘长征陈翠忠宋亚萍魏震

石河子大学学报（自然科学版） 2021年2期

钱立鹏，刘长征*，陈翠忠，宋亚萍，魏震

(1 石河子大学信息科学与技术学院，新疆石河子 832003;2 石河子大学水利建筑工程学院，新疆石河子 832003)

径流序列的形成受多方面因素影响，是一种高维非线性系统。20世纪以来，由于城镇化、气候等影响[1]，河流的径流量发生了变化，导致河流径流量不确定性增强。高精度的河流径流量预测能为下游水库放水、洪水预测等提供有价值的水文信息。随着PC机处理能力的提升及遥感、卫星气象数据的获取方便，数据驱动方法取得了普遍关注，最常用的是基于仿生人脑神经系统的人工神经网络(ANN)模型和支持向量机(SVM)模型[2]，这2种模型具有对非线性问题强大且灵活的表达能力，常用于模拟工程中的非线性行为，从而简化复杂工程的过程，但传统的神经网络一般是单层的或隐性的双层，在训练的时候往往容易陷入局部最优。

国内外学者对径流量模拟做出了许多研究，初海波等[3]对径流样本序列分类，并利用ANN、SVM模型探讨不同预报因子对径流模拟的影响；朱明飞等[2]基于水土评估工具(SWAT)模型研究和模拟影响玛纳斯河流域径流演变的因子组成成分；李慧等[4]同样利用SWAT对玛纳斯河日径流进行了模拟；李文倩等[5]结合地形指数和融雪量利用改进后的TOPMODEL模型对流域日径流进行预测，预测的精度较高；刘艳等[6]依据流域径流周期规律，采用集合经验模态分解(EEMD)-差分自回归滑动平均(ARIMA)组合模型对年径流序列进行有效预测；金君良[7]等对数值预报产品利用期望最大化(EM)算法进行后处理，采用秩评分的方式评价预报准确性和有效性，结果表明对数值预报产品进行良好的前处理和后处理可以有效提高流域内径流预报的精度；DELAFROUZ H 等[8]提出一种新的空间重构技术的混合神经网络(GEPNN)进行USUG提供的密西西比河、珠江和马斯金格姆河三个地点河流日流量的预测；NACAR S等[9]采用可变神经网络，将网络在13种不同滞后时序下组成不同模型对土耳其东部黑河流域进行短期流量预测，最终发现多元线性回归网络(MLP-NN)和主成分分析网络(PCA-NN)相对于总径流线性流量模型(TLR-RR)表现更优；BAFITLHILE T M 等[10]采用SVM和ANN模型对昌化、陈河、志丹流域进行洪水预测，结果表明SVM模型预测的结果更好。

综上所述，虽然前人已经做了大量的研究，但由于水文预测的不确定性极大、影响因素很多，提高流域径流预测模型的精度和稳定性仍是径流量预测的难点。本文采用更深层次的数据挖掘模型DBN对已有的水文数据进行日径流预测，与粒子群优化的支持向量机(PSOSVM)、SVM和前馈神经网络(FFNN)3种数据驱动模型的预测结果进行对比分析，研究DBN模型在流域日径流预报上的有效性和稳定性。

1 研究区域及方法

1.1 研究区域及数据来源

玛纳斯河流域呈扇形分布，总面积约为 3.099万km2。玛纳斯河径流量的35.3%来源于积雪融水，是玛纳斯河径流量补给的重要源头[11-13]。肯斯瓦特水文站(高程值900 m，控制区域5 156 km2)位于玛纳斯河干、支流汇合后的出山口处，本文选取该站1984—2000年共6 120天的实测降水、气温、蒸发量、径流量日平均值数据开展预测。

1.2 研究方法

自HINTON G提出采用多层受限玻尔兹曼机(RBM)对FFNN的初始权重和阈值进行预训练构成DBN以来[14]，深度挖掘数据特征已经广泛应用于各种工程领域。在不同流域径流量预测应用中，基于机器学习的数据驱动模型总体上取得了好的效果。

前馈神经网络(FFNN)是一种基于人脑神经系统的智能动态模型，有大量并行处理系统组成，具有强大的拟合和估计非线性序列的能力[15]。网络结构由神经元数量、层数(输入层、隐层、输出层)和连接各层的权重向量组成，各层间采用全连接方式。各层间的连接权重和阈值采用误差反向传播算法[15]进行调整，隐层和输出层上的映射函数分别使用sigmoid函数和linear函数。支持向量机(SVM)模型是一种基于统计理论的智能模型，由于该模型已经被证明在做回归、分类和时间序列预测上准确度高，在水文研究中已被应用[2,10]。

本文运用DBN对日径流序列进行预测时分为预训练和FFNN训练2个阶段，在预训练阶段，采用对比散度算法[14]和吉布斯采样方法对隐层和可见层重构2次；预训练完成进入FFNN训练阶段，此阶段隐层和输出层上不同的激活函数下模型输出不同。本文借鉴文献[15]的方法预测Dez水库径流量，当得到隐层和输出层上sigmoid和linear二个传输函数时会得到较好的准确率。网络权值调整采用误差反向传播拟合输入和输出参数之间的关系，在训练平衡后得到稳定的权值和阈值输出。在训练过程中，网络的能量E是不断减小的[15]，整体误差也是不断减少的，然而当模型训练到与训练样本重合时，过度拟合的情况就会出现，所以，本文验证集在验证训练模型过程中误差开始增加时，网络应该停止训练，此时获得的权重和阈值就是最小误差模型的匹配值[15]。

为了进行日平均径流量预测，将玛纳斯河流域肯斯瓦特站1984—2000年204个月6 120天的数据划分成训练集、验证集和测试集，其中3 100天作为网络训练数据，1 000天作为验证数据，2 020天作为测试数据。采用判定系数R2、均方误差MSE、预测时间t和模型参数数量作为判定模型预测有效性、稳定性的指标[9]，其中预测时间t是4种模型在内存为8G，CPU为1.9 GHz的个人64bit PC机下使用相同软件MatlabR2014a进行预测的时间。

2 结果与分析

2.1 参数率定

4种模型各经过30次实验后得到各模型预测时的最优参数。由图1可见：FFNN采用3-5-1结构，隐层确定5个神经元时效果最好，学习率为0.01(图1a)，预测的相对误差如图1e所示。SVM确定高斯核函数系数σ为1.414，损失函数值ε为0.707时预测效果最好(图1b)，预测的相对误差如图1f所示。PSOSVM中确定种群数量为20，进化200代，粒子的位置和速度随机生成，个体速度更新的弹性系数为0.9，群体速度更新的弹性系数为1，该参数优化下确定SVM的高斯核函数系数σ为8，损失函数值ε为0.5时预测结果最好(图1c)，预测的相对误差如图1g所示。DBN的底层采用2层RBM，每层确定3-2的结构，即可见层3个神经元，隐层2个神经元，预训练完成后顶层采用3-5-1结构，隐层中确定5个神经元，训练时将3 100天训练集划分成31批数据以提高计算效率，学习率为0.01，连接权重初始化为来自正态分布N(0,0.01)的随机数，隐层阈值初始化为0，可见层阈值初始化为log[pi/(1-pi)]，其中pi表示训练样本中第i个特征处于激活状态的概率。为了避免过拟合，在梯度项后添加了权衰减项c=0.006，吉布斯采样的采样步数k=2，交替采样2步后，获得的样本可以很好的近似RBM所定义的分布，预测结果如图1d所示，预测的相对误差如图1h所示。

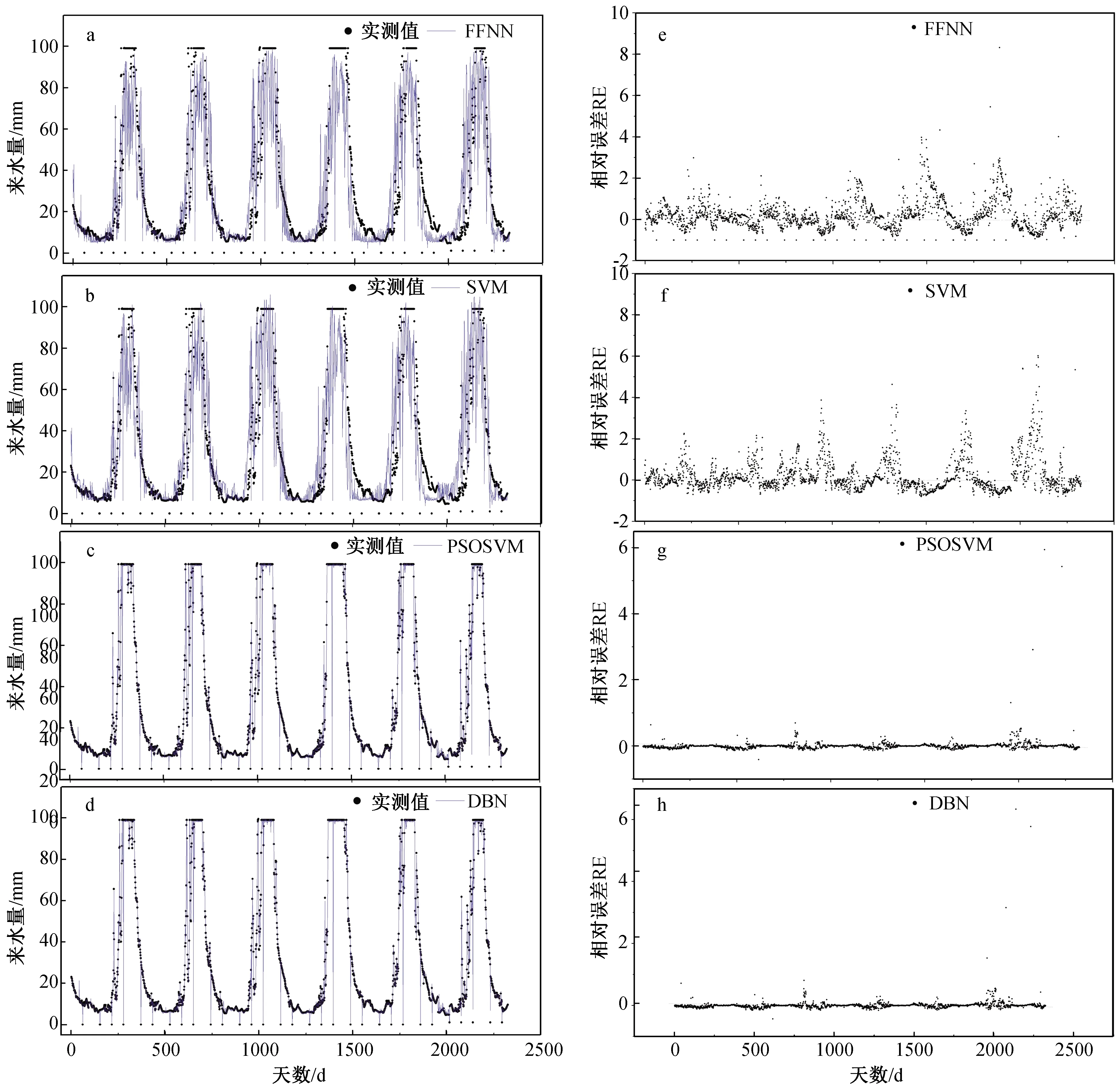
图1 预测结果和预测相对误差

2.2 对比分析

从图1可知：

(1)PSOSVM和DBN预测准确率优于SVM和FFNN。其原因主要是PSOSVM采用PSO算法优化SVM中的核参数，而PSO算法全局寻优能力强，所以经过优化后的SVM模型预测的准确率大大提高。

DBN预测准确率也优势明显，原因是其深度挖掘数据特征能力比FFNN更强，训练前期采用多层的RBM进行网络预训练时，数据内部的深层特征被进一步挖掘，因此，预训练完成后FFNN的权重和阈值比普通预测时随机初始化更优，可寻找非线性问题全局最优解的能力明显提高。

(2)PSOSVM和DBN预测出的准确率非常相近。在人文活动日益加剧，气候变化导致降雨量、蒸散发量等气象因素发生大幅演变，流域内下垫面发生巨大变化，地表径流和地下径流发生改变，预测的随机性不断增强的情况下，DBN的预测效果更优，其主要原因在于DVB先对FFNN进行了有效的权值和阈值的预训练，预训练使FFNN训练的初始权值更优，对于非线性问题的拟合能力更强，而且由于径流序列是严重的非平稳序列，因此，DBN在预测时充分发挥了深度数据挖掘上的优势，取得了比其它3种模型更优的预测效果。

图2是4种不同模型的预测准确率，表1是4种模型在其它方面性能的对比结果。

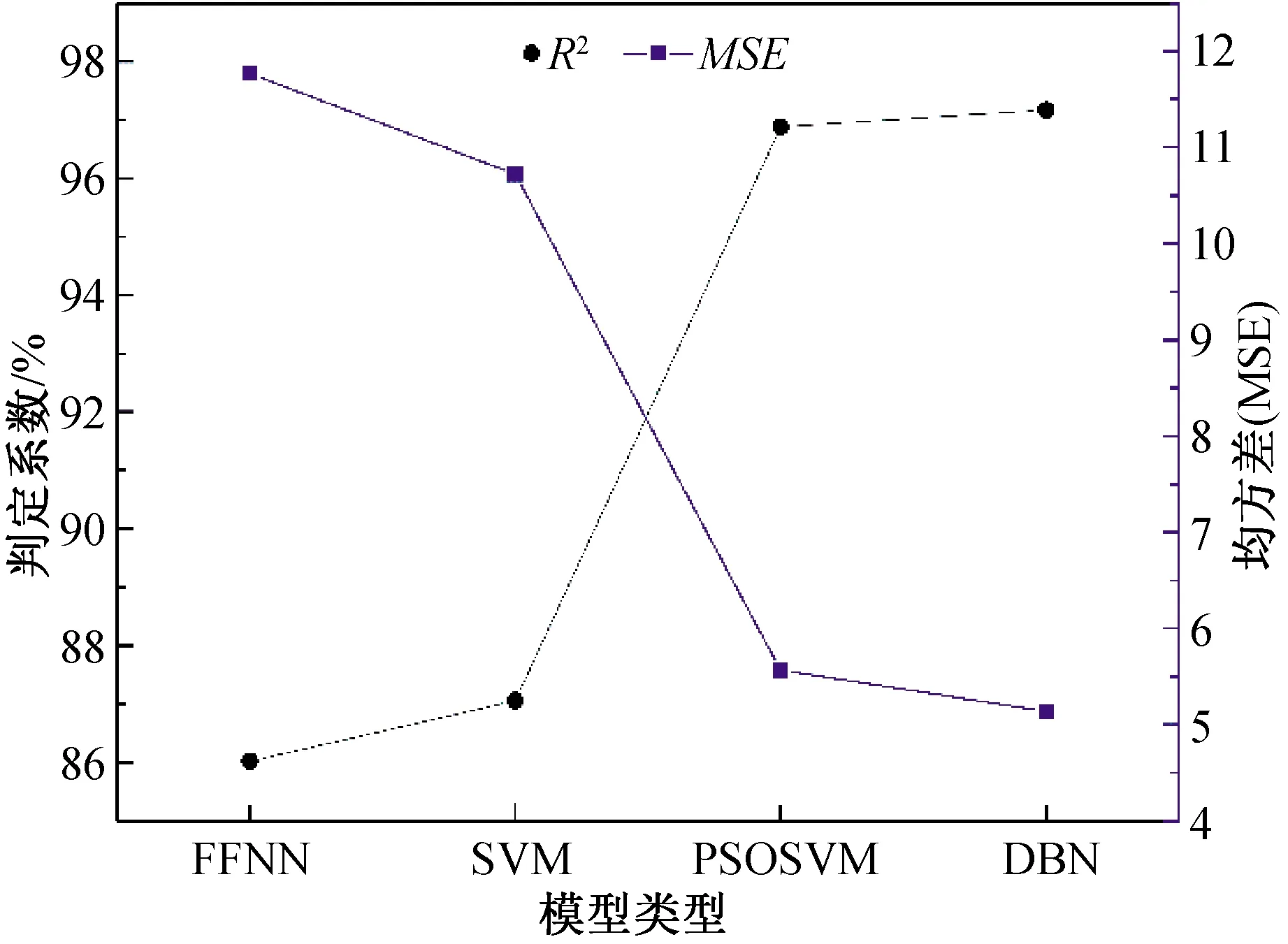
图2 精确度性能对比

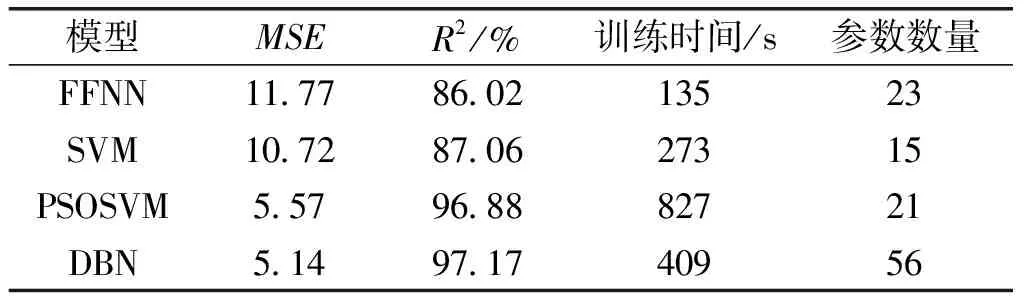
表1 模型性能对比

从图2和表1可知：

(1)DBN和PSOSVM在预测准确率上分别为97.17%、96.88%，但在相同的软硬件条件下，DBN的预测时间只有PSOSVM算法的0.5倍。这表明在实际预测应用中DBN比PSOSVM的适用性更强。

(2)从各个模型的参数数量看，SVM所需设置的参数最少，DBN需设置的参数最多，DBN采用对比散度算法和吉布斯采样只需进行1次采样便可以得到足够好的近似分布，但是本文实验为保证高预测准确率使用2次采样，收敛时间并没有比SVM增大很多。

SVM模型是一种通过非线性的高维映射将数据样本映射到高维空间，尽管采用合理的核函数后运算复杂度大大减小，但是核函数中参数的设置对于预测准确率有非常大的影响。因此，使用PSO算法进行SVM参数优化后，尽管预测准确率从87.06%提升至96.88%，但是消耗的时间也增加了3倍多，参数的数量也有所增多。

(3)从均方误差看，PSOSVM和DBN的误差相差很小，都能取得良好的准确率。

综上可知：总体上DBN的精度与PSOSVM相差较小，但明显优于SVM和FFNN模型；在适用性上，DBN在保持精度的前提下，用时只有PSOSVM的0.5倍，其适用性明显强于其它3种模型；从简便性看，SVM需要设置的参数最少，但是其预测精度比PSOSVM和DBN要低。因此，在玛纳斯河流域进行径流量预测时，DBN在精度和适用性上都优于其它3种模型。

3 讨论

利用DBN预测取得良好预测效果的原因主要如下：

(1)从研究的地理区域上看，肯斯瓦特站具有特殊地理位置，位于狭窄的出山口处，径流量变化较大。另外，由于近年来城镇化建设和频繁的人文活动，该地区局域性气候变化，致使降雨量、融雪量等发生大幅改变，引起下垫面的变化，地表水和地下水位发生改变，导致该区域径流演变的不确定性增大，径流序列成为严重的非平稳序列，这些随机性变化大大增加了径流量预测的难度。DBN由于特殊的网络构成层次，其深度数据挖掘和非线性问题的拟合能力比其它3种模型更强。

(2)从特殊时间点的预测结果看，在一些极端径流演变的点上，FFNN、SVM的预测误差都很大，出现这种情况的原因数据测量时，外界环境的变化和测量仪器精度误差带来一定的噪声，这些噪声在数据进行影响分析时没有被完整剔除掉，另外，玛纳斯流域人文活动日益加剧导致径流序列成为复杂的非平稳序列，演变的随机性和复杂性产生极端径流量，测量出的“极高”和“极低”的径流量在实际中代表该站发生洪涝和干旱的预警。

这种极端演变情况的发生主要是由肯斯瓦特站上游气温和降雨的变化引起的，而且城镇化的发展致使局部水循环发生改变影响了该流域气温、蒸散发量、降雨量等气象数据的变化。因此，拟合结果中对极端径流量的预测精度对整个模型的整体性能影响巨大。

(3)从不同模型对于研究区径流量实际拟合能力看，FFNN、SVM由于本身网络层次不深，对于非线性复杂问题的拟合能力相对不足，故其整个网络的性能相对于PSOSVM较差;而DBN由于采用了更加合理和深层次的对初始权重的预训练结构，不仅网络的层次加深，而且各层对于影响径流变化的因子数据间复杂特征的提取能力加强，所以在持续时间长的日径流预测上能获得相对于其它3种模型更好的效果。

由于PSOSVM为了得到SVM的良好初始参数而引入了PSO算法进行训练，故其训练的复杂度增加、训练时间延长，并且从本质上看，PSOSVM和SVM在影响径流量变化的因子数据的内部规律挖掘上并无差距，这二点是PSOSVM在径流量预测过程中预测效果低于DBN的主要原因。

综上所述，人文活动带来玛纳斯河流域径流量演变序列的随机性和非平稳性，DBN比FFNN、SVM、PSOSVM在对该流域未来径流预测上可以产生很好的预测效果。