概率论与数理统计在信息论中应用分析

赵金梦 中移（苏州）软件技术有限公司

为深入研究更佳的信息容量和信息通行方式，信息论应运而生，其为人们立体而直观的展示了信息相关因素之间的联系[1]，具有较高的应用价值。而作为信息论的重要研究支撑，概率论和数理统计意义非凡，可保障信息流通科学性、稳定性、交融性即联系性等。

一、现代信息论内涵分析

分析信息论内涵可以看出，其应用工具和领域主要为概率论与数理统计和信息与计算科学，其主要研究信息在时间和空间领域中的流通情况[2]。其研究模型主要由信源、信宿、信道、编码器及译码器等元素构成，且各个元素之间拥有特异性的规律联系。相较于传统信息模式，现代信息论拥有更加更广的范围、应用方式也更安全，可适应各种应用场景，比如遥控传递信号、电话实时双向通道及立体信息传统模式（语音、图像、文字等同步传递）等。当然，概率与数理统计为信息论基础，因此信息论也会重视信道噪声和信源符号的概率统计，而将其进行概率归集，可形成具有规律的语法信息，比如语用和语义等。

当然，从信息概念和内涵的定性，可充分结合概率论的偶尔事件，例如抛硬币形成的正面和反面说。由此，可对信息进行以下归结：其主要描述物体的动态情况，或其不确定的存在模式。以这一维度切入可以发现，对于信息的理解，可将其归结为对信息的不确定因素的描述，如其变化范围或不同的变化状态。由此，概率论与数理统计和信息论之间拥有紧密的联系，可更好的融入概率论。

二、概率论与数理统计作用分析

概率论与数理统计主要是指利用统计概率方式，破解学习、生活及工作等领域问题，因此其拥有明显的作用：首先：降低问题解决难度。即通过该工具可搭建数理问题便捷通道，优化计算过程，提升效率；其次，可为相关研究提供一定支撑，即利用该工具形成的基础模型，可深层次剖析研究对象，提升研究质量，比如通信问题研究、化学反应时间的研究及服务系统的研究等；其三，可兼容于其他学科，提升教学效果。即将其核心理念融入其它学科类型中，比如信息论等[3]。这样便能将该学科立体而直观的展示在学生面前，降低学生学习难度，提升其学习兴趣，进而达到提升教学效果的目的；其四，可助力信息数据化的现代化发展。概率论和数理统计可以三维方式展示信息发展构架，理清互联网信息数据之间的联系，进而实现信息数据的时代发展计划，以推动网络世纪信息论的深化发展。当然，概率率和数据统计作为一种动态发展的学科，其还能进一步升华信息数据化。

三、概率论与数理统计于信息论应用途径

（一）概率统计于通信系统中的应用

在信息论中通信系统属于框架支撑部分，其体系化构成如图1 所示，其中较为关键的为信源、信道及信宿等，以信源和信道为例：

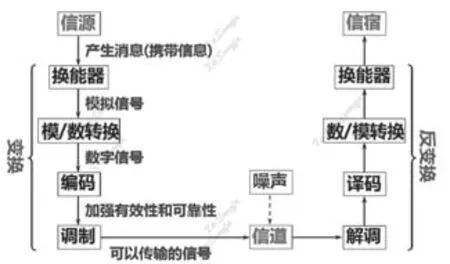
图1 通信系统基本框架

前者主要是指信息的源头，其发射出的信息是无规律的。因此能以随机变量方式展示其这些信息。即：以m 表示无规律的随机信息，由此其信源发出的信息集合能以m={m1，m2，m3mn}表示，其分布情况能以{p（m），m ∈m}来表示，其信源则能以{m，p（m）}来表示。

后者主要是指信息流转的通道，即在信息进入相关通道后，由于存在随机干扰，因此输入与输出信号存在差异性，从而形成具有依赖的差异函数关系。由此，若输入信号为k{k}，那么其输出信号为h{h}，而{p（p（h|k）|k）：k ∈k，h ∈h}为其转移概率。而在信号源发射信号中，信号的输入和输出在信道之间传递，由此可用C={k，p（k|h），h}表示。

而通过以上信道和信源组成的模型，可用以下统计公式表示：

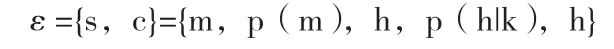
（二）最优编码中概率统计的应用

编码是信息论的关键表现，属于概率统计核心应用环节之一。在信息论中，通信过程中信号传递的真实性是较为关键的基础问题，而编码则能以一定方式提升信源信息质量，使其拥有相应抗干扰能力和传输效率[4]。当然由于信源发射的信号属于波动状态，具有不确定性和随机性，因此具有一定概率性。即若编码越长，则其概率越小，若编码较短则其概率越大。由此，应有相关标准来确定最优码。例如，在统计编码概率应用过程中，对于变长编码相关内容：首先，设定变长编码为f，其中以S 表示信源头，具体为{x，p（x）}。尤此其量的长度可以表示为f（x），如此，对于变长编码的标准可以表示为：L（s，f）。同时由于概率被计算到变长编码的标准内容中，因此能以加权平均表示其出现概率，即相应的数学期望；其次，定位最优编码。在上述内容基础上，以f0表示仅能编译信号，那么可得出以下概率范围：L（L，f）≥L（s，f0），其中最为编码可用f0表示。从而得出最优编码为仅能编译长信号。而对于此处的最优编码信号，则拥有多种方式，例如在概率分布基础上形成的算码法、Huffman 技术等。其中使用较为广泛的为Huffman 编码技术，其在信源概率趋势基础上，形成自身编码表和数据压缩表，其中码长较长对应小概率，码长较短对应大概率，进而得出相关数据证明。

（三）信息度量中概率统计的应用

对于信息论而言，信息度量属于核心成分。以理论为角度赌气进行剖析可以看出，其是指可以利用相关工具，度量信息，进而提升信息确定性。由此，不确定性属于信息度量的基础和依据。对于此项问题的解释，可充分利用随机变量知识对其进行预期计算和统计，以其概率展示相关内容，即：因为能用随机变量来展示信源发射的信息，所以对于信息的度量能用不确定性的随机变量来表示。比如，用m 表示离散随机比爱良，那么可用（p1，p2，p3，pm）等表示其概率分布，其中分布函数可以用不确定的变量来表示，若其中m 是定性分布，那么其没有确定性，即为0，若m 是可能分布，那么拥有最强的随机性，即不确定性为mmax。在此基础上，可将散随机变量X 的不确定性记为：Q（X）=Q（p）=Q（p1，p2，p3，p4，……，pn）如p 为等概率分布，则可将记为Q（p）=g（a）。依据概率统计中不确定性内涵，可判定函数Q（m）具有的性质为：可加性。如有一组整数w i，i=1，2，3，4， ……，m， 如，则可确定：g（a）= g（w i）+H（w1’，w2’，w3’，w4’，……，w m’），在上述关系中，wi’=wi/a，此时，可以证明，如满足上述条件可唯一确定函数H（p）的形式，即：H（p1，p2，p3，p4，……，p n）=不确定的函数（香农熵）。

四、结语

综上，在信息通信背景下，概率论与数理统计拥有十分中重要的价值意义，即能程序化推动信息论学科的进步，为其相关研究奠定良好基础，以促进其深化发展。由此可以看出，两者实际拥有较为密切的联系，相关人员应理清两者的关联因素，挖掘应用价值，提升概率统计工具于信息论的应用效能。于此，文章就其实应用进行了三个方面梳理，具有一定参考价值。当然其中仍存在一定不足，在此希望相关学者能深入其中，研究既符合两者作用价值发挥的应用方式。