非均质物料链式组合称重定量算法优化与试验
2021-05-12龚中良
龚中良,张 镇
非均质物料链式组合称重定量算法优化与试验
龚中良,张 镇
(中南林业科技大学机电工程学院,长沙 410004)
非均质物料质量差异较大且不可分割,组合称重定量过程中组合对象不确定,存在组合称重定量精度与组合速度的矛盾。该研究针对链式组合称重定量系统,提出以定量精度及组合效率为目标,对组合样本数和抽样数进行优化分析,达到保证组合称重定量精度下,减少数据计算量以提高组合定量速度的目的。研究表明,在相同允许组合误差下,增大组合样本数可提高组合成功概率,但组合计算量随组合样本数增加而呈指数增加。通过对服从正态分布(100, 102)的质量数据进行10 000轮组合计算发现,当组合定量目标质量为500 g,允许组合误差为0.1 g时,组合计算时间较短的组合样本数为14。并对优化组合样本数和抽样数的组合算法进行了链式组合称重定量试验验证。试验结果表明,在物料质量标准差≤30 g,允许定量组合误差为0.1 g时,优化后的组合算法与优化前遍历组合算法在定量组合成功概率总体上保持在95%左右,且优化后的算法组合计算时间减少了40%。研究结果可为非均质物料链式组合称重定量系统的研制提供参考。
算法;优化;链式组合称重;非均质物料;定量精度;效率;误差分析
0 引 言
由于单体称重定量组合速度低下,难以满足市场定量称重的需求[1-3],随之出现的组合称重定量装置可提供快速,准确、可靠的操作[4-5],在食品定量称重上发挥着重要作用[6-10],尤其是在农产品定量称重方面。国内外众多学者对不同物料组合称重定量算法做了大量研究,并取得一定的成果,如Keraita等[11]对组合秤提出一种基于位运算的组合算法;Imahori等[12]提出使用动态编程来编写主控逻辑,以加速组合速度。唐志祥等[13]对组合秤进行了较初步的介绍和组合工作原理探究;邓志辉等[14]针对不同物料的给料性能之间的差异,进行仿真试验研究,对于不同的物料,选取出较佳组合秤漏斗总数配置和组合算法,但是组合速度没有得到大幅提升;刘乘等[15]对组合秤进行了模型仿真研究,主要通过固定每次称重单元数和每次参与组合的单元数来探究不同运行模式下的组合状态;安世奇等[16]对物料组合顺序进行排序遍历;穆庆霖[17]将组合算法拆分为组合计算和组合控制两部分来进行组合计算和组合逻辑控制。以上研究对颗粒状均质物料适应性较好,可满足生产需求;对非均质个体物料,组合称重定量性能却不尽人意。由于非均质物料具有不可分割性,流动性差,质量相对较大且分布不均匀等特点[18],如仍采用像粉状或者颗粒状物料一样缓慢振动式加料,则单个物料对组合结果影响较大,势必对加料稳定性以及定量组合算法快速性、精确性提出更高要求。为解决非均质物料组合称重定量存在的组合定量精度与组合计算速度之间的矛盾,本文针对链式组合称重定量系统,以定量精度及组合效率为目标,对非均质物料链式组合称重误差进行了分析,探讨组合样本数和抽样数对组合定量误差、组合计算速度及定量组合成功概率的影响,并进行了试验验证,以期为非均质物料链式组合称重定量系统开发提供参考。
1 链式组合称重定量系统及组合定量工作原理
链式组合称重定量系统由输送机构和控制系统组成,输送机构为链式组合称重定量装置,如图1所示。该装置可连续称重而不影响机器运行动态[19],物料盘固定安装在链条上,通过链传动带动物料盘运动,在传送链输送过程中完成数据采集、数据处理、数据组合计算、数据输出等功能。
物料盘直立且不施加侧向力时,物料盘整体可看作悬臂梁结构,运用力矩公式可得物料实际质量和测得质量之间的关系。如图2所示,设物料支撑架点为力矩参考点,物料的重力1(N)相对于点的力臂设为1(m),物料盘整体及称重垫片的重力2(N)相对于点的力臂设为2(m),称重传感器所测得质量为(kg),相对于点的力臂设为0(m)。由力矩平衡得:
式中为重力加速度,m/s2;1=。为物料的实际质量,kg。
则物料的实际质量为
1.物料盘 2.称台垫片 3.称重传感器 4.称重支架 5.光电传感器 6.卸料执行器 7.物料 8.物料收集箱 9.链条 10.链轮 11.传动电机
1.Material tray 2.Weighing platform gasket 3.Weighing sensor 4.Weighing bracket 5.Photoelectric sensor 6.Unloading actuator 7.Material 8.Material collection box 9.Chain 10.Sprocket 11.Drive motor
图1 链式组合称重定量装置结构图
Fig.1 Structural schematic diagram of chain quantitative combination weighing device
注:1为物料的重力(N),2为物料盘整体及称重垫片的重力(N),为力矩参考点,0为称重传感器所测得质量相对于点的力臂(m),1为物料的重力相对于点的力臂(m),2为物料盘整体及称重垫片的重力相对于点的力臂(m)。
Note:1is the gravity of the material (N),2is the gravity of the whole material tray and the weighing pad (N),is the moment reference point,0is the arm of the mass measured by the weighing sensor relative to point(m),1is the arm of the gravity of the material relative to point(m),2is the arm of the gravity of the whole material tray and the weighing pad relative to point(m)
1.称重传感器 2.物料盘 3.物料 4.称重垫片 5.支撑架
1.Weighing sensor 2.Material tray 3.Material 4.Weighing gasket 5.Support frame
图2 称重传感器受力分析图
Fig.2 Force analysis diagram of weighing sensor
链式组合称重定量系统工作流程如图3所示。首先链传动连带物料盘向前传送进料,物料盘依次经过称重区域的称重垫片到达不同链位处,称重传感器安装在称重垫片的下方进行质量数据的采集[20],通过光电传感器触发称重传感器采集信号并记录定位每个物料盘的位置,物料盘在传送链运转下依次被输送到不同链位对应的卸料执行器处,当采集到的质量数据个数达到设定好的组合样本数时,系统开始进行定量组合计算,如果定量组合结果满足误差要求,则表示组合成功,驱动对应链位的卸料执行器进行卸料[21],把物料盘装载的物料卸下,卸料过程链传动保持继续传输;如果组合失败,卸料执行器不动作,传送链继续传送物料,称重传感器继续采集物料质量数据,进行下一次的组合,依次运行,直至接收到暂停或者停止指令。
2 组合定量误差分析
误差主要包括称重传感器误差和组合定量误差。称重传感器误差[22-24]主要由系统误差和随机误差组成,其中系统误差可以通过误差补偿来修正[25-26],随机误差在组合定量时可部分抵消。此外,由于随机误差的量级远小于组合定量误差,因此本文不考虑称重传感器误差的影响;组合定量误差为非均质物料组合后与定量值之间的差值,与组合样本数,抽样数及组合方式密切相关,而这些因素对组合算法具有重要影响。
组合计算一般采用2种算法[27-28]。一种是速度优先型算法,即在遍历所有组合,在运算过程中,第一次出现满足组合定量误差的结果就表示组合成功,这种算法的优点就是速度较快。当组合样本数为8个进行组合时,组合时间平均为80 ms,允许组合误差为±0.2%,但组合定量误差在允许组合误差内随机性较大;另一种是精度优先型算法,通过遍历所有可能的组合,在这些定量组合成功的结果中找寻组合定量误差最小的组合作为最后结果,这样虽然精度有所提高,但是组合计算时间增加。当组合样本数为8个进行组合时,允许组合误差为±0.2%,平均需要120 ms,它每次组合定量结果均为本轮误差最小的组合。当组合样本数更大时,组合时间还会更长。为了同时满足较高的组合定量精度及组合速度要求,本文对组合样本数和抽样数进行了优化分析。
2.1 组合样本数n和抽样数r对组合次数和组合误差的影响
当组合样本数为时,遍历所有可能的组合,组合次数共有:
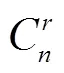
当样本数和抽样数分别以1为步长,从1取到20时,对应的组合次数如图4所示。
由图4可知,当样本数一定时,组合次数随着抽样数的增加先增加后减小,且呈对称分布,在中间达到最大值;当抽样数一定时,组合次数随着样本数的增加而增加,抽样数为样本数一半时,趋势尤为明显,在样本数大于15左右快速增加;组合次数的骤增,定量组合成功概率将越大,精度也将可能越高,但样本数的增加,将导致组合算法的计算量呈指数增长,系统运算时间也会大大增加。为了平衡组合定量的准确性和组合运算时间,需对样本数和抽样数进行优化选择。
2.2 抽样数r的确定
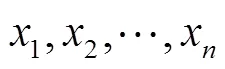

2.3 抽样数r对组合成功概率的影响
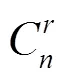
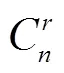
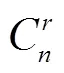
3 误差优化及试验
3.1 确定最佳样本数n
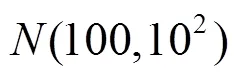
由图5可知,组合成功概率和组合计算时间随着样本数的增加而增加,当允许组合误差为0.05 g时,组合成功概率增加速度呈近似线性增加,在样本数为16时,组合成功概率才能达到95%以上;当允许组合误差为0.10~1.00 g时,组合成功概率随着样本数的增加呈现先保留快速后缓慢增加的趋势。这是因为前期样本数增大,数据组合次数随之增大,而误差范围相对较大,故符合误差范围的组合较多,组合成功概率呈较快增加,组合计算时间增加缓慢;到后期由于数据量骤增,所需的组合计算时间快速增加,而组合成功概率由于前期增加过快,后面趋于饱和,故缓慢趋近于1;此时,当样本数增加到14时,组合成功概率已经达到96%以上,组合计算时间为20 s左右,当样本数继续增加到16时,组合成功概率达到99%以上,但是组合计算时间上升到之前的3倍60 s左右。综合考虑组合成功概率和组合计算时间,当允许组合误差为0.05 g时,为保证组合成功概率,样本数应选择16以上为佳;当允许组合误差为0.10 g时,选择样本数为14较佳。
3.2 优化抽样数r的试验
根据前文对抽样数的论证,该试验对其进行验证。设计试验质量数据传递规律按照链式移位进入称重传感器。选择组合样本数为14,物料质量分布服从正态分布(100,2),为物料质量标准差,组合定量的目标质量为500 g,优化选取抽样数。测试在10 000轮组合计算下对不同标准差和不同误差范围内的组合成功概率的影响,并将其改进前组合算法进行对比,结果如表1。改进前的组合算法为从小到大进行顺序遍历组合的算法。试验结果为组合成功概率、组合计算时间和时间缩短比例。具体试验步骤如下:
1)程序依次产生14个服从正态分布的随机数;
2)对数据进行异常值的剔除;本试验样本数为14,故采用公式(5)中22和22对数据进行剔除,选定显著值指标为=0.05,查临界值表得临界值为0(14,0.05)=0.546;
4)在14个数据中进行个数据组合计算,如果组合结果满足允许误差,则组合成功,组合成功对应物料数据清0;否则组合失败,一次组合结束。
5)继续生成1个正态分布数据按链传动规则依次传递进来,14个位置依次移位,直到14个位置对应的数据都不为0,再继续进行下一次组合,即步骤2),如此循环直至结束。

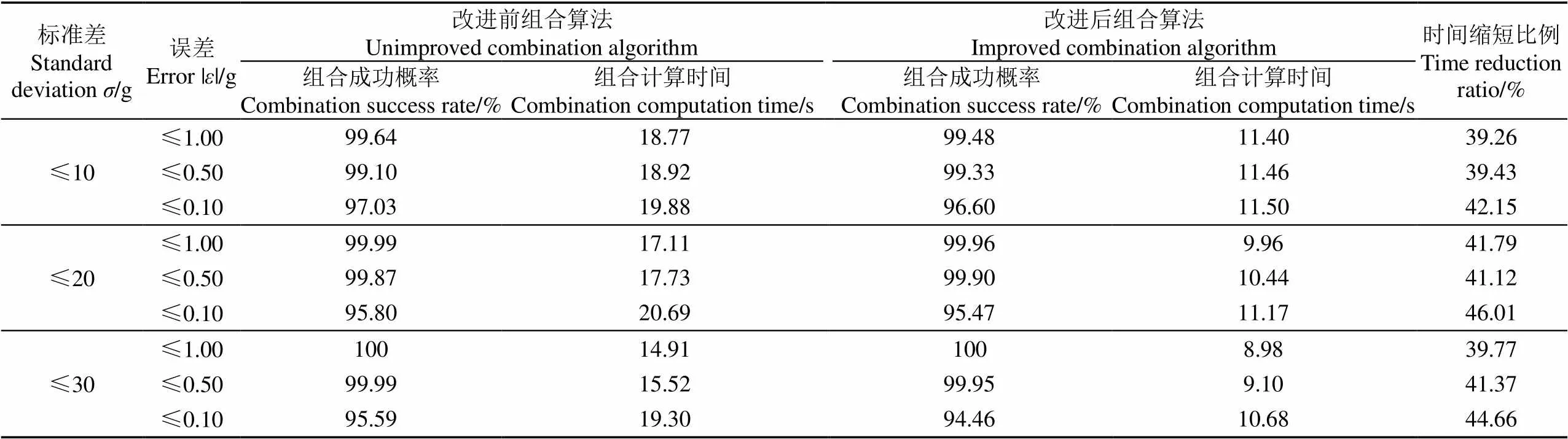
表1 改进前后组合算法的组合成功概率和组合计算时间对比
3.3 试验验证
为验证优化后组合算法性能,搭建试验平台如图6所示。以砂糖橘作为物料,其符合非均质物料质量分布特性,单个物料质量对整体组合称重定量影响大等特点。经测试单个砂糖橘质量范围服从正态分布(34,62)。组合定量目标质量为100 g,组合样本数为14。试验结果如表2所示。

表2 砂糖橘定量组合试验结果
由表2可知,砂糖橘组合定量试验中,允许组合误差为0.1~1.0 g时,优化后的定量组合算法的组合成功率可达到95%以上,组合计算时间在1.5 ms以内,满足系统使用要求。
4 结 论
本文以链式组合称重定量系统为基础,对组合定量误差进行分析,提出以精度—效率为目标,选定组合样本数和抽样数进行数学分析及优化,得到最佳的参数。并通过试验验证,具体结论如下:
1)组合成功概率随着组合样本数的增加而增加,但组合计算量也呈指数增加。综合考虑组合成功概率与组合速度,发现当允许组合误差为0.1 g时,较优的组合样本数为14;
2)通过理论分析得到的抽样数能保证定量组合计算精度和组合成功概率;
3)在物料分布标准差一定时,误差越小,组合精度越高,但其组合成功概率会降低,组合计算时间也会增长;
4)改进后的组合算法在保证组合成功概率的情况下,组合计算时间较传统组合算法减少了40%左右。
[1]张丽妹,高占宝,尹志兵. 基于等效系统的动态称重数据处理[J]. 测控技术,2013,32(6):33-35,43.
Zhang Limei, Gao Zhanbao, Yin Zhibing. Dynamic weighing data processing based on equivalent system [J]. Measurement and Control Technology, 2013, 32(6): 33-35, 43. (in Chinese with English abstract)
[2]叶志刚. 影响移动定量包装精度的因素及对策[J]. 石油化工自动化,2013,49(6):72-74.
Ye Zhigang. Factors and countermeasures affecting the accuracy of mobile quantitative packaging[J]. Petrochemical Industry Automation, 2013, 49(6): 72-74. (in Chinese with English abstract)
[3]张春友,吴晓强. 新型智能组合秤称重系统[J]. 自动化仪表,2015,36(4):88-90.
Zhang Chunyou, Wu Xiaoqiang. New intelligent combination scale weighing system[J]. Automation Instrumentation, 2015, 36(4): 88-90. (in Chinese with English abstract)
[4]Clark N M. Multi-head weighting apparatus: U.S. Patent 9217661[P]. 2015-12-22.
[5]Keraita J N, Kim K H. A study on the optimum scheme for determination of operation time of line feeders in automatic combination weighers[J]. Journal of Mechanical Science and Technology, 2006, 20(10): 1567-1575.
[6]PNarkhede P, Dhawale R, Karthikeyan B. Microcontroller based multihead weigher[J]. Indian Journal of Science and Technology, 2016, 9(30): 1-5
[7]张俊,熊家慧,郭爱云. 定量包装控制系统的设计与实现[J]. 包装工程,2016,37(13):134-139.
Zhang Jun, Xiong Jiahui, Guo Aiyun. Design and implementation of quantitative packaging control system[J]. Packaging Engineering, 2016, 37(13): 134-139. (in Chinese with English abstract)
[8]权小青. 我国智能组合秤市场发展分析[J]. 衡器,2012,41(12):1-3.
Quan Xiaoqing. Analysis on the development of my country's intelligent combination weigher market[J]. Weighing Apparatus, 2012, 41(12): 1-3. (in Chinese with English abstract)
[9]张加营,张凤,马云天. 一种智能定量包装秤[J]. 衡器,2015,44(12):12-13.
Zhang Jiaying, Zhang Feng, Ma Yuntian. An intelligent quantitative packaging scale[J]. Weighing Apparatus, 2015, 44(12): 12-13. (in Chinese with English abstract)
[10]张西良,毛翠云,路欣. 粉粒状农用产品混合式自动定量包装研究[J]. 农业工程学报,2003,19(2):121-125.
Zhang Xiliang, Mao Cuiyun, Lu Xin. Research on mixed automatic quantitative packaging of powdered and granular agricultural products[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2003, 19(2): 121-125. (in Chinese with English abstract)
[11]Keraita J N, Kim K H. A weighing algorithm for multihead weighers[J]. International Journal of Precision Engineering and Manufacturing, 2007, 8(1): 21-26.
[12]Imahori S, Karuno Y, Nagamochi H, et al. Kansei engineering, humans and computers: Efficient dynamic programming algorithms for combinatorial food packing problems[J]. International Journal of Biometrics, 2011, 3(3): 228-245.
[13]唐志祥. 包装计量组合秤工作原理初探[J]. 广东工学院学报,1994(1):45-52.
Tang Zhixiang. Preliminary study on the working principle of the packaging and measuring combination weigher[J]. Journal of Guangdong Institute of Technology, 1994(1): 45-52. (in Chinese with English abstract)
[14]邓志辉,张西良,刘剑敏,等. 组合秤组合模型对定量误差影响研究[J]. 机械设计与制造,2006(3):108-110.
Deng Zhihui, Zhang Xiliang, Liu Jianmin, et al. Research on the influence of combination model of combination weigher on quantitative error[J]. Machine Design and Manufacturing, 2006(3): 108-110. (in Chinese with English abstract)
[15]刘乘,李彩娟,沈训乐. 组合秤仿真及优化研究[J]. 包装工程,2011,32(3):53-56,59.
Liu Cheng, Li Caijuan, Shen Xunle. Simulation and optimization of combination weigher[J]. Packaging Engineering, 2011, 32(3): 53-56, 59. (in Chinese with English abstract)
[16]安世奇,孙瑞. 多功能组合秤控制系统设计及优化算法研究[J]. 电子测量技术,2019,42(7):108-112.
An Shiqi, Sun Rui. The design and optimization algorithm of the control system of the multifunctional combination weigher[J]. Electronic Measurement Technology, 2019, 42(7): 108-112. (in Chinese with English abstract)
[17]穆庆霖. 组合秤的称重系统设计及优化[D]. 青岛:青岛科技大学,2020.
Mu Qinglin. Design and Optimization of Weighing System of Combination Scale[D]. Qingdao: Qingdao University of Science and Technology, 2020. (in Chinese with English abstract)
[18]邓志辉,张西良. 组合秤物料给料性能对定量误差影响研究[J]. 中国计量,2005(9):52-54.
[19]Li B, Li Y, Wang H, et al. Compensation of automatic weighing error of belt weigher based on BP neural network[J]. Measurement, 2018, 129: 625-632.
[20]李光梅,魏新华,李法德,等. 水果综合分选机称重模块的设计与实现[J]. 农业工程学报,2009,25(2):96-100.
Li Guangmei, Wei Xinhua, Li Fade, et al. Design and implementation of weighing module of fruit comprehensive sorting machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(2): 96-100. (in Chinese with English abstract)
[21]康宁波,强锋,吴龙国,等. 基于电磁式同步执行机构的鲜枣分级机设计与试验[J]. 农业工程学报,2017,33(7):254-260.
Kang Ningbo, Qiang Feng, Wu Longguo, et al. Design and experiment of synchronization actuator system based on electromagnetism for fresh jujube classifier[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(7): 254-260. (in Chinese with English abstract)
[22]闫文吉,陈红亮,陈洪敏,等. 硅压阻式压力传感器测量误差在线补偿方法研究[J]. 仪器仪表学报,2020,41(6):59-65.
Yan Wenji, Chen Hongliang, Chen Hongmin, et al. Research on on-line compensation method for the measurement error of silicon piezoresistive pressure[J]. Chinese Journal of Scientific Instrument, 2020, 41(6): 59-65. (in Chinese with English abstract)
[23]谢永华,孟凡虎. 双孔平行梁式称重传感器非线性校正研究[J]. 现代科学仪器,2010(6):64-66,70.
Xie Yonghua, Meng Fanhu. Research on nonlinear correction of double-hole parallel beam load cell[J]. Modern Scientific Instruments, 2010(6): 64-66, 70. (in Chinese with English abstract)
[24]李巨韬,郭伟,王建. 平行梁式电容传感器极板耦合角位移计算和分析[J]. 传感技术学报,2013,26(4):492-497.
Li Jutao, Guo Wei, Wang Jian. Calculation and analysis of coupling angular displacement of parallel beam capacitive sensor plates[J]. Journal of Sensor Technology, 2013, 26(4): 492-497. (in Chinese with English abstract)
[25]朱鹏飞,黄松和,梅菊. 组合秤称重传感器大变形致非线性误差分析[J]. 包装工程,2015,36(23):103-106,115.
Zhu Pengfei, Huang Songhe, Mei Ju. Analysis of nonlinear error caused by large deformation of load cell of combination weigher[J]. Packaging Engineering, 2015, 36(23): 103-106, 115. (in Chinese with English abstract)
[26]章胜. 普洱饼茶连续生产线中毛茶自动定量装置研究[D].昆明:昆明理工大学,2016.
Zhang Sheng. Research on the Automatic Quantitative Device of Maocha in the Continuous Production Line of Pu'er Cake Tea[D]. Kunming: Kunming University of Science and Technology, 2016. (in Chinese with English abstract)
[27]孙前明. 组合称重微机控制系统的研究与开发[D]. 镇江:江苏大学,2002.
Sun Qianming. Research and Development of Combined Weighing Microcomputer Control System[D]. Zhenjiang: Jiangsu University, 2002. (in Chinese with English abstract)
[28]孙瑞. 多功能组合秤控制系统设计及优化算法研究[D]. 青岛:青岛科技大学,2019.
Sun Rui. Multifunctional Combination Weigher Control System Design and Optimization Algorithm Research[D]. Qingdao: Qingdao University of Science and Technology, 2019. (in Chinese with English abstract)
[29]张西良,邓志辉,李萍萍. 组合秤组合性能分析与仿真研究[J]. 农业机械学报,2005,36(12):64-66,46.
Zhang Xiliang, Deng Zhihui, Li Pingping. Combination performance analysis and simulation study of combination weigher[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(12): 64-66, 46. (in Chinese with English abstract)
[30]王林,孙芳. 利用狄克松判别法剔除观测数据粗差[J]. 江西测绘,2016(4):18-20.
Optimization and experiments of non-uniform objects quantitative combination algorithm based on chain transmission
Gong Zhongliang, Zhang Zhen
(,,410004,)
Effective mass of non-uniform objects varies differently and indivisibly, thereby making the combined object uncertain during the combined weighing and quantification process. Thus, there is a great contradiction between the quantitative accuracy of combined weighing and combined speed. In this study, a chain-drive combination weighing and quantitative system was proposed, where the precision-efficiency was treated as the combined operation target. A combined error of influence parameters was analyzed to evaluate the accuracy of combined weighing quantification. Besides, the number of combined samples and sampling were optimized to reduce the combined calculation time with a high combined quantitative speed. The results indicated that the number of combined samples increased the probability of combination success. However, the amount of combined calculation increased exponentially with the increase of the number of combined samples. Thus, the number of combined samples needed to be optimized for the tradeoff between the combined error and calculation time. A normal distribution was followed after 10 000 rounds of combined calculation on the quality data, where the mean value was equal to 100, and the variance was 102. It was found that the number of combined samples was 14 with the shorter calculation time when the target mass of combined quantification was 500 g and the allowable combined error was ±0.1 g. Moreover, the sampling numbers needed to be screened for the high requirements of combined error, due to the characteristics of non-uniform objects. In addition, a simulation experiment was designed to explore the influence of the total sampling number on the combined error and calculation time. The test results showed that the improved and previous combination maintained the success probability of quantitative combination at about 95% when the standard deviation of weight distribution was less than 30 g and the combined quantitative error was less than 0.1-1.0 g. The calculation time of the optimized combination was reduced by 40%, compared with the conventional one. The findings can provide a sound reference for the potential development of a chain combined weighing and quantitative system for non-uniform objects.
algorithm; optimization; chain quantitative combination weighing; non-uniform materials; quantitative accuracy; efficiency; error analysis
龚中良,张镇. 非均质物料链式组合称重定量算法优化与试验[J]. 农业工程学报,2021,37(5):310-316. doi:10.11975/j.issn.1002-6819.2021.05.036 http://www.tcsae.org
Gong Zhongliang, Zhang Zhen. Optimization and experiments of non-uniform objects quantitative combination algorithm based on chain transmission[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(5): 310-316. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.05.036 http://www.tcsae.org
2020-08-09
2021-02-09
湖南省科技计划重点研发项目(2016NK2151);湖南省科技计划重点研发项目(2018NK2066)
龚中良,博士,教授,研究方向为机电一体化技术与应用。Email:739472786@qq.com
10.11975/j.issn.1002-6819.2021.05.036
TH715; TP391.9
A
1002-6819(2021)-05-0310-07
