高职物流课堂信息化教学探索

李芸嘉

摘  要：职业教育的信息化实践研究旨在解决高职院校教学中存在的教师演示受限、学生参与度低、课堂效率低等问题。文章以“节约里程法”为例，从课堂演示与实践计算两个角度，利用希沃白板、EXCEL、节约里程法软件等进行了信息化教学探索。

关键词：高职物流教育;信息化教学;节约里程法

中图分类号：G712    文献标识码：A

Abstract： The informatization practice research of vocational education aims to solve the problems of limited teacher demonstration， low student participation and low classroom efficiency in higher vocational colleges. In this paper， taking the“mileage saving method”as an example， from the two perspectives of classroom demonstration and practical calculation， we explore the information-based teaching by using the Seewo whiteboard， EXCEL and mileage saving method software.

Key words： higher vocational logistics education; information teaching; mileage saving method

节约里程法是高职物流《仓储与配送管理》课程中“配送路线优化与设计”部分的内容，也是现代物流三大成熟模块（仓储、配送、运输）中配送模块的重要知识，在职业院校技能大赛“智慧物流仓储”赛项与物流管理“1+X”证书考核中均有涉及。根据海南经贸职业技术学院物流管理专业人才培养方案设计，学生属首次接受“配送路线”相关知识，因此对配送路线优化并无理性认识，属于零起点。因此，提高传统课堂的信息化教学含量，将教学内容直观化，帮助学生克服畏难心理对于提升最终教学效果都有深刻影响。

节约里程法是一种常用的解决车辆数目不确定的启发式算法，使用節约里程法的主要思路是根据配送中心的运输能力和配送中心到各个用户以及各个用户之间的距离来制定使总的车辆运输的吨公里数最小的配送方案。

节约里程法的计算步骤共分4步：（1）最短距离计算;（2）节约里程计算;（3）节约里程排序;（4）配送路线连结。4个步骤为层层递进的关系，每一步骤的错漏都会导致下一步骤乃至最后步骤的出错。而在上述4个步骤中，步骤（1）、（2）、（4）均有易错点，因此该方法较适合以信息化教学手段加以突破。

本文以一道节约里程法例题为例，从课堂讲授与软件解题两个角度，讲述各步骤的关键点以及信息化手段的突破应用。如图1所示为一个配送网络。（P）为配送中心所在地，（A）～（J）为客户所在地，括号内的数字为配送量，单位为吨（t）;线路上的数字为道路距离，单位为公里（km）。

1  课堂讲授角度的信息化探索

根据课前分析，确定该知识点的重点为节约里程法的计算步骤，难点为节约里程法的矩阵计算与连线。因此，首先解决重点，按节约里程法的4个步骤将就“节约里程法”微课视频分拆为4部分，分段播放，同时利用希沃白板软件中课堂活动“选词填空”功能，将前3个步骤的内容采取选项填空的方式完成，增强学生的互动。

步骤（4）为图上连线，传统课堂往往将图1画在黑板上进行连线讲解，反复擦拭，既费时费力，学生也容易丧失兴趣，此处应在演示的环节施加信息化教学辅助。笔者于2019年借助adobe软件开发FLASH课件，将连线界面做成互动界面，如图2所示。左侧的线路与右侧表格中的“连接点”均可通过点击变成红色，再度点击恢复原样。由此可做路线连线的授课展示，直观灵活，容易试错，在几轮的授课讲解中取得了良好的课堂效果。

2  方法计算角度的信息化探索

首先是步骤（1）最短距离矩阵的填写，此处需要找到图上两点间的最短距离，如图3所示。由于该步骤只能通过人工观察寻找，且两点间的通路往往不止一条，所以容易出错，如EB两点之间的通路就有E—P—B，E—D—C—B，E—不知名点

—C—B三条路径可选择，距离分别为8+9=17，6+5+5=16，5+4+5=14。此处需尽力找寻两点间准确的最短通路，然而结果在此步骤不可验证，因此需要到第（2）步进行检验，以免后续出错。

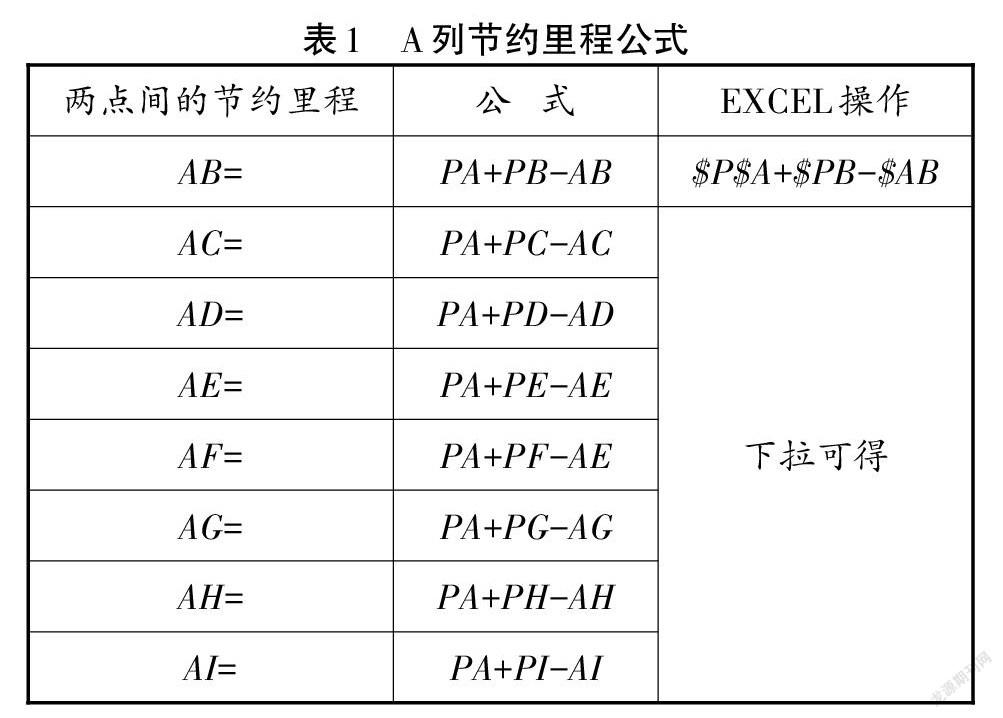
接下来是步骤（2）节约里程矩阵的填写，如图4所示。该步骤的计算方法基于节约里程法的原理“三角形两边之和大于第三边”的原则，以图4中点AB间的节约里程计算为例：AB间的节约里程等于PA+PB-AB，此处PA，PB，AB的取值来自在图3中得出的两点间的最短距离，故AB间的节约里程等于10+9-4=15。步骤（2）的计算不算复杂，但重复计算较多，人工计算浪费时间，且易出错。另外，此处可对步骤（1）的取值是否正确及进行验证，因此引入EXCEL进行公式计算。以图4中第二列为例，通过列表（表1）可发现此处的计算规律。因此，在从A到H的每一列的第一个单元格，对公式中相同的部分进行锁定，即可下拉得到矩阵整列的数值。

此处值得一提的是，步骤（2）节约里程矩阵中的最小值为0，也就是优化前后并无节约的里程，当节约里程矩阵的计算出现负值的时候，即可对相关数据进行检验，证明前面的最短距离寻找有误。另外，还有一种情况会造成节约里程法矩阵的计算出现负值，该方法的网络资源鱼龙混杂，部分习题资源本身出题有误，在设置各点间距离的时候，并未检验任意三点的三角形遵循两边之和大于第三边的原则，因此造成后续的错误。因此，在教学资源的选择上，教师应对网络开放资源及教材资源预先检验计算，避免上述错误的产生。

无论后续（3）、（4）步选择人工计算绘图或软件的方式，前面都需要通过EXCEL的计算和检验确保两个矩阵数值的正确。笔者在CSDN网站下载到“节约里程法”计算程序，软件需要手动录入步骤（1）中的最短距离矩阵，车辆载重限制与单圈路线的长度限制即可，为确保录入数值的正确，利用EXCEL先做数据检验，再将相关信息录入“节约里程法”软件可得到带有方向的配送路线设计结果，如图5至图8所示。

在前面的探索中，希沃白板、FLASH交互提升了课堂演示的直观性与教学趣味性，EXCEL与节约里程法软件提升了计算效率，确保了计算的准确度。随着信息技术的发展，信息化教学手段在克服传统课堂的低趣味、低效率、少互动的问题上，起到越来越重要的作用，本次围绕“节约里程法”知识点的信息化教学实践也是一次符合信息时代教学的成功探索。

参考文献：

[1] 陈新鸿. 基于excel操作的节约里程法在配送路线选择中的应用[J]. 物流工程与管理，2013，35（2）：98-100.