考虑HI理论和在线监测误差的配电网可靠性评估

顾佳浩，淡淑恒

（上海电力大学电气工程学院，上海 200090）

传统配电网可靠性评估多以历史统计数据为基础，通过统计数据得到设备历史故障率来进行配电网的可靠性评估[1-2]，由此计算得到的可靠性指标具有滞后性。针对这一问题，有学者通过对设备历史故障率进行修正，实现可靠性的动态评估。文献[3]考虑了天气、设备运行年限，对设备故障率进行修正，但影响设备故障率的因素还包括负载率、鸟害、外部异物[4]等因素。文献[5]将设备历史运行状况、实时运行状况、气候条件3个因素综合考虑得到设备的故障率，但其中实时运行状况仅根据电流的变化来判定设备故障率，判断指标单一、不全面。以上评估方法虽然对历史故障率进行了修正，但修正参数还是根据历史统计数据得到，例如：天气的分类由统计年来确定，时效性不强。

近年来，电力系统中引入了以设备实时运行状态为评价基础的健康指数HI（health index）理论[6-7]。HI是根据人体健康状况评价方法而提出的设备健康度指标。对电力设备进行健康度评价的研究大多基于模糊数学理论[8-11]。如果单纯使用模糊数学理论，容易造成信息的丢失，也不能解决指标间的信息重复。文献[12]通过例行实验、在线监测、带电检测等手段得到设备的状态分值，但该分值是依据设备某项指标不达标，运用扣分准则得到的，没有具体给出健康度评价模型。

对设备进行在线监测是设备健康度评价的重要手段。然而，在线监测装置是在温度骤变、强电磁场环境中运行的，不可避免地受到恶劣天气和严峻的电磁场环境的影响，从而影响采集信号的精度，甚至损坏装置[13]。量测数据不准确必将导致电网的状态评估受到影响。文献[14]通过构建的可信虚拟网络来评估电网数据的可信度。文献[15]分析了量测数据丢失对配电网态势的影响，提出了一种鲁棒递推滤波方法，减轻了配电网状态评估精度对量测数据丢失的敏感度，为后续研究提供了思路。

综上，本文通过对配电网主设备建立评估指标体系，提出了一种基于设备健康度评估模型的配电网可靠性评估方法，根据设备实时HI得到的实时故障率对配电网进行可靠性的实时动态评估。同时，提出监测数据精度模型，对实时故障率进行修正，并考虑了监测数据不准确对可靠性的影响。

1 设备指标与权重确定

1.1 指标体系

表征配电网主设备健康度的指标有很多，根据全面、主导、可操作的原则，选取对设备健康度有直接影响的指标作为设备健康度的评价指标。例如：变压器的运行状态与油中溶解气体、绝缘性能、电气性能、绝缘油性能、运行环境等因素有关，选取的二级指标应以上述一级指标为主导。本文参考了文献[12]中关于设备指标的选取要求，对变压器、电力电缆、架空线、断路器4类设备建立指标体系，各类指标如表1～4所示。根据指标类型，可将指标分为定性指标和定量指标，其中定量指标又可分越小越优型指标、越大越优型指标、中间型指标。表1～4中，★为在线监测指标；↓为越小越优型指标；↑为越大越优型指标；→为中间型指标；不做标记的为定性指标。

表1 变压器指标Tab.1 Indexes of transformer

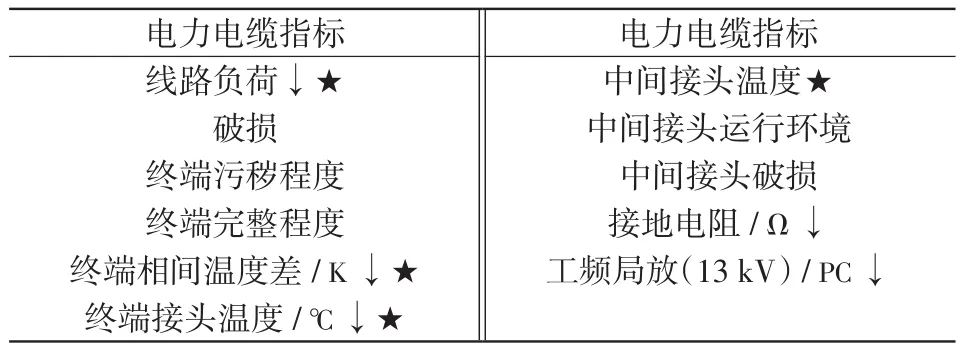
表2 电力电缆指标Tab.2 Indexes of power cable

表3 架空线指标Tab.3 Indexes of overhead line

表4 断路器指标Tab.4 Indexes of circuit breaker

1.2 指标权重

设备的评价指标对设备健康度的影响程度不同。为了使设备最终的HI能够反映被评价设备的健康状况，应对各项指标赋予不同的权重。序关系分析法[16]是一种常用的权重赋权方法，该方法将定性分析与定量分析相结合，根据相邻指标间的相对重要性确定权重，具有计算流程简单的特点。序关系分析法的流程如下。

步骤1对指标的重要性进行相互比较，并按指标X的重要程度进行排序，即

式中，m为指标个数。

步骤2确定相邻指标间的相对重要程度，即

式中：Ck为相邻指标相对重要程度的比值；k=m，m-1，…，3，2；Xk为第k个指标的相对重要程度 。

步骤3权重计算公式为

式中，pk为第k个指标的权重 。

2 设备HI模型

设备的HI是根据设备的多个状态量指标打分后加权计算得到的。引入HI对设备状态量指标打分，最高分为100分，表示该状态量处于最佳状态；最低分为0分，60分为危险值，小于60分表示状态量处于恶化状态。定性指标的打分规则和定量指标的取值范围见附表A-1～A-4。

2.1 指标的HI

2.1.1 定性指标

某些指标（如设备污秽程度）不易直接测量，故可通过巡检等方式并根据专家经验直接进行打分；某些指标是达标性指标，即满足一定范围就可打满分，若不满足则酌情打分。以上两类指标均为定性指标。

2.1.2 定量指标

定量指标是指可以量化的指标，根据预防性实验、在线监测、带电检测等手段测量得到。由于配电网设备指标量纲不一，数据数量级差别大，故将指标进行规范化处理。将定量指标分为越小越优型指标、越大越优型指标、中间型指标，并对文献[7，17]的相关研究模型进行改进，根据改进后的模型对设备各指标健康值进行打分。

（1）当指标实际值越小时，性能越优，则定义该指标为越小越优型指标，其表达式为

式中：hi为设备第i个指标的HI；yi为第i个指标的实际值；ymin、ymax分别为正常运行指标的最小值和最大值。以越小越优型指标为例，当yi=ymin时，hi=100分，表示该指标处于最佳状态；当yi=ymax时，hi≈60分，表示该指标处于恶化边缘；当yi＞ymax时，hi=0分。此时该指标处于恶化状态，对设备健康极为不利。

（2）当指标实际值越大时，性能越优，则定义该指标为越大越优型指标，其表达式为

（3）当指标的实际值为正常运行范围之间的某个值时性能最优，偏离此值性能变差，则定义该指标为中间型指标，其表达式为

式中，yo为中间型指标的最优值。

2.2 设备HI

设备HI由各指标加权计算得到，即

式中：H为设备的HI；pi为第i个指标的权重。

3 设备故障率与HI的关系

工程上广泛采用的配电主设备健康指数H与设备实时故障率λ的关系[18]可表示为

式中：K为比例系数；C为曲率系数。

求解式（9）必须有两组设备的HI与故障率的数据。根据最小故障率λmin和平均故障率λa可以求解式（9）。由于各地配电网因设备厂家及运维水平的差异，导致各地电网公司统计得出的设备故障率存在差异，因此本文计算参考了我国2015年中压配电网元件平均故障率[19]，以此为平均故障率λa。由于最小故障率数据较难获取，因此本文参考文献[17，20]的相关研究结果，故障率数据见表5。

表5 配电网主设备故障率Tab.5 Failure rate of key equipment in distribution network

根据表5数据，最小故障率λmin对应的设备HI为100分，平均故障率λa对应的设备HI为80分。这样可以得到待定系数K和C的计算式分别为

通过计算得到的设备的HI与实时故障率的关系式如表6所示。

表6 设备HI与设备故障率的关系Tab.6 Relationship between health index and failure rate

随着技术的发展，设备的质量可靠性将稳步提升。因此，可以根据设备的大量积累数据进行统计分析后对式（9）进行修正。

4 考虑监测数据精度的可靠性评估

4.1 设备故障率修正模型

在线监测装置内部是低电流、低电压运行环境，而装置却处在干扰信号多样的环境中，如高低频扰动、电磁场干扰等。这些干扰信号一旦侵入在线监测装置，必将对监测数据准确性产生影响，从而影响设备HI，进而影响设备故障率计算。

在线监测装置在整个“服役”期间，其精度受干扰程度是不同的。图1为在线监测装置精度变化曲线，其中，α(t)为在线监测装置精度，0＜α(t)≤ 1；t为装置投运时间；T1为装置开始老化时间；T2为装置运行寿命。由图1可知，从装置开始投运至T1时间段内的“服役”中，在各种抑制干扰措施下，装置性能较稳定，精度不受环境的干扰，处于α(t)=1的稳定期；当“服役”年限超过T1后，由于装置内部零件开始老化，内部电路不稳定，装置更容易受到环境的影响，且精度随着运行年限逐年下降，故T1～T2称为老化期。

图1 在线监测装置精度变化曲线Fig.1 Accuracy curve of online monitoring device

在线监测装置精度α(t)可表示为

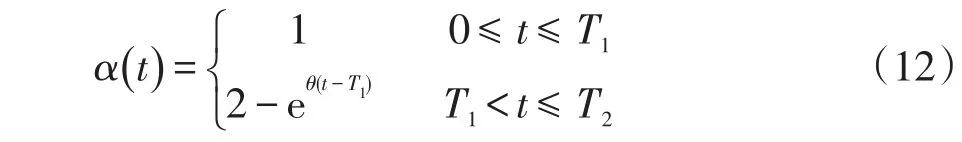
式中，θ为老化系数，与装置本身性能有关。

在线监测装置精度下降直接影响在线监测指标实际值的测量偏差，且不能确定最终结果到底是偏大还是偏小，故得到的修正值是一个范围，即

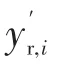
式中：H′为修正后的设备HI；n为设备的在线监测指标个数；hf,i为非在线监测指标的HI；λ′为设备修正故障率。

4.2 可靠性评估指标

本文以系统平均停电频率SAIFI（system average interruption frequency index）、系统平均停电持续时间SAIDI（system average interruption duration index）、平均供电可用率ASAI（averageserviceavailabilityindex）3个指标为可靠性评估指标。各指标计算公式分别为

4.3 可靠性评估方法

故障模式影响分析FMEA（failure mode and effect analysis）法是配电网可靠性评估的基本方法之一，FMEA法以每个线路元件为对象，分析其故障后果，形成事故影响报表。根据负荷点的故障集，从事故影响报表中提取相应的故障后果，计算负荷点的可靠性指标。本文采用FMEA法进行可靠性评估。该方法可靠性评估流程如图2所示。

图2 可靠性评估流程Fig.2 Reliability evaluation process

5 算例分析

IEEE RBTS BUS-2配电系统如图3所示。

图3 IEEE RBTS BUS-2配电系统Fig.3 IEEE RBTS BUS-2 distribution system

对图3中的IEEE RBTS BUS-2进行配电网可靠性实时评估，故障率数据采用图2中的设备实时故障率。故障定位隔离时间、联络开关切换时间、故障点上游恢复供电时间分别取1.83 h、1.53 h、0.83 h，电力电缆、架空线、断路器、变压器的修复时间分别取7 h、5 h、5 h、6 h，不考虑隔离开关和联络线故障。算例中其他参数详见文献[21]。

5.1 不同故障率数据的可靠性对比分析

5.1.1 设备HI与算例可靠性计算

由于配电网设备指标的典型值获取较困难，故本文算例涉及的设备指标实际值是根据Matlab中的均匀分布unifrnd函数生成。4类设备的指标权重如表7所示，且4类设备的指标权重值与表1～4的指标先后顺序一致。

表7 设备指标权重Tab.7 Weights of equipment indexes

由表7数据可计算出算例系统所有设备的HI与故障率，结果见图4。

图4 设备HI及其故障率Fig.4 Equipment HIand failure rate

由图4可计算出馈线F1～F4与算例系统的可靠性指标，计算结果见表8。

表8 馈线与系统可靠性指标Tab.8 Reliability indexes of feeders and system

5.1.2 采用历史故障率的可靠性计算

传统的配电网可靠性评估中，设备的故障率是根据往年同类设备的不同投运年限对应不同故障情况统计得到的，且遵循浴盆曲线的规律[3]，如图5所示。图5中，λ(Y)为设备故障率；Y为设备投运年限；t1、t2分别为区域Ⅱ的开始和结束时间。区域Ⅰ中，由于设备安装不当等原因，导致设备比较容易出现故障，称为磨合期；区域Ⅱ中，设备运行稳定，称为稳定期，在该区域内，设备故障率近似为常数，可取为该类设备的平均故障率；区域Ⅲ，设备受老化影响，故障率开始上升，称为老化期。

图5 设备故障率浴盆曲线Fig.5 Bathtub curve of equipment failure rate

以算例馈线F1为例计算可靠性。该条馈线上所有设备均采用统计得到的历史故障率数据，且假设设备均处于浴盆曲线的区域Ⅱ，则设备的故障率数据为该类设备的平均故障率，设备的平均故障率见表5，由此可计算馈线F1的可靠性。采用不同故障率计算得到的可靠性指标如表9所示。

表9 不同故障率下馈线F1的可靠性Tab.9 Reliability of feeder F1at different failure rates

由表9数据可知，采用实时故障率计算得到的可靠性是实时动态的，而采用历史故障率不能实时反映配电网的可靠性。因为可靠性受到设备运行状况及外部环境例如恶劣天气等因素的影响。若设备在一段时间内均运行在浴盆曲线的稳定期，则这段时间内计算得到的可靠性指标将保持不变，这与实际情况不符。

5.2 监测数据精度对可靠性的影响

在线监测装置开始老化时间取T1=5 a，装置寿命T2=10 a，当投运年限t=10 a时，装置精度取0.95，则老化系数θ=ln1.05/5，分别计算监测装置投运年限为5～10 a时，馈线F1～F4及系统可靠性的变化量，这里只考虑精度影响下设备故障率最大时的情况。投运年限与SAIFI变化量关系见图6。

图6 投运年限与SAIFI变化量关系Fig.6 Relationship between operation period and changes in SAIFI

由图6可以得出如下结论。

（1）随着在线监测装置投运年限的增加，装置从第5年初开始精度下降，馈线F1～F4的可靠性指标SAIFI都有不同程度的增加。

（2）在线监测装置投运年限越长，馈线可靠性指标SAIFI增加越快。由于在线监测装置精度模型呈指数分布，装置投运年限越长，精度下降越明显。

（3）馈线F3的SAIFI变化随装置投运年限的增加最为敏感，而馈线F2的变化敏感度最低。由表8数据可知，4条馈线中，馈线F3的可靠性最差，而馈线F2的可靠性最好。由此可知，SAIFI变化的敏感程度与不考虑精度变化时馈线最初的可靠性好坏呈负相关。馈线最初的可靠性越差，则可靠性变化越敏感。

5.3 不同分布函数对设备HI的影响

为研究指标数据由不同分布函数生成对设备HI的影响，调用Matlab中的正态分布normrnd函数得到设备指标的实际值，计算各类设备的HI平均值，并与由均匀分布计算得到的设备HI平均值进行比较。各类设备的HI平均值及变化量见图7。

图7 不同分布的设备HI与变化量Fig.7 Equipment health indexes and their changes under different distributions

由图7可知，当指标实际值由正态分布得到时，变压器、电力电缆、断路器的HI平均值都有不同程度的增加，且断路器增加最明显，而架空线路的HI平均值有所减少。由于均匀分布生成的数据不受指标类型的影响，且生成的指标数据都在正常范围之内，即指标最低分为60分；而正态分布生成的数据受到指标类型的影响，中间型指标比其他指标更容易得高分。若设备的中间型指标越多，则设备的HI越高，但由正态分布产生的数据可能在正常范围之外，即该指标为0分。实际实验中，架空线路有若干个指标数据在正常范围之外，导致这些指标HI为0分，最终导致平均分减少。而断路器的中间型指标最多，权重占比为0.466 9，远多于其他设备，因此断路器的平均分增加最明显。由此可见，设备HI与指标类型和分布函数类型有关。

6 结语

本文根据配电设备指标类型，提出了一种基于设备健康度评估模型的配电网可靠性评估方法。该方法克服了传统可靠性评估指标具有滞后性的缺点，实现了配电设备健康度的量化及配电网可靠性的实时动态评估，具有时空辨识性。同时提出了设备故障率修正模型，考虑了监测数据不准确对可靠性的影响，使得可靠性评估结果更加接近工程实际。