智能配电网状态估计研究现状和展望

郑文迪 ，聂建雄 ，邵振国 ，许启东 ，曾祥勇

（1.福州大学电气工程与自动化学院，福州 350116；2.福建省电器智能化工程技术研究中心，福州 350116）

随着分布式电源DG（distributed generation）以及主动负荷大量渗透到配电网，新一代配电网中负荷与电源间的互动将日益增强，同时DG所具有的随机性、波动性和分散性等特点导致配电网功率流随机性增强，配电网的运行与控制方式变得更为复杂，调度难度提升[1-2]。为了应对配电网数据的迅速增长，保证配电网实时安全稳定的运行，发展智能配电网已成为共识。

为了使配电网可靠、经济、安全的运行，配电管理系统需要对配电网运行状态进行全面准确地分析[3]。作为智能配电网态势感知的基础，状态估计通过对实时量测数据的分析和计算排除错误信息的干扰，为配电系统提供更加可靠精确的数据。配电网中的远程终端单元RTU（remote terminal unit）、同步相量量测单元PMU（phasor measurement unit）和高级量测体系AMI（advanced metering infrastructure）等装置采集的量测数据作为状态估计的运行基础，将采集的数据进行清洗剔除不合格的数据，完成后利用状态估计算法对状态量进行估计，并将其用于其他高级应用，总体过程如图1所示。

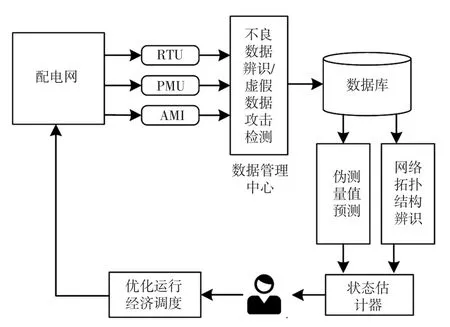
图1 配电网状态估计功能示意Fig.1 Schematic of state estimation function for smart distribution network

在智能配电网中存在下列问题：①需要监测的点多面广，考虑建设成本等因素，无法全部配置量测装置，使信息监测盲点很多；②电力电子设备的高比例应用使电压等级低，容量较小的配电网中谐波和噪声相对基波的比值增大，会对量测值产生比较大的影响[4]；③新能源发电量和负载呈现出常态化的随机波动和时空不确定性，使配电网局部区域电压和电流波形变化更为显著。这些问题使配电网量测数据的可信度降低，导致传统配电网量测装置和状态估计技术难以满足智能配电网估计精度的要求。

为了实现配电网更高精度的测量目标，PMU和AMI被越来越多地运用在配电网中[5-6]，这些量测装置在提高配电网量测精度，增强网络可观性的同时也需考虑以下因素。

（1）由于经济、技术等因素的限制，大规模配置PMU并不现实。需在计及状态估计可观度的基础上，建立具有经济性、DG与负荷不确定性、估计精度及局部电压越限概率影响的PMU优化配置模型，使PMU的使用效益最高。

（2）配电网数据来自不同的量测体系，量测采样的时间尺度及同步性方面存在较大差异，需对多源量测数据进行融合，提高信息的一致性。

（3）大量的量测数据对有限的通信网络造成严重的负担，发生通信故障的频率变高，数据碰撞、数据丢包和时钟跳变的现象更加严重。

（4）更加开放的通信环境，使向数据采集系统注入虚假数据和删改原数据的网络攻击有了可趁之机。

本文通过对现有的配电网状态估计算法进行梳理，从量测延时、量测丢包、混合状态估计和虚假数据注入攻击等方面概述了配电网状态估计的研究现状，并对今后值得关注的研究方向进行展望。

1 配电网状态估计算法

1.1 静态状态估计

以加权最小二乘法WLS（weighted least square）为主的静态状态估计是电力系统中运用最为成熟的状态估计算法[7]，其本质是求解如下函数优化问题：

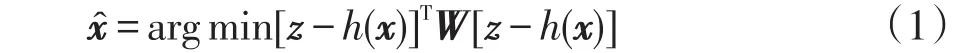
式中：z为m维量测矢量；x为n维状态矢量；为需要估计出的最优状态量；h为量测函数；W为量测权重矩阵，W∈Rm×m，表示量测数据的精度。

静态状态估计已发展多年，但是仍面临以下挑战。

（1）传统WLS每次迭代均需重新计算雅可比矩阵，计算效率低。为了提高静态状态估计的计算速度，需开发出求解效率更高的状态估计算法。当前输电网常用的是快速超级解耦估计FSDE（fast super decoupled estimation）[17]，若将其直接用于配电网，由于配电网中支路阻抗比绝对值较大，可能出现算法收敛性变差甚至无法收敛的情况。如何使FDSE在高阻抗比的配电网中具有良好的适应性是静态状态估计所面临的一大挑战。

（2）配电网中配电变压器和馈线线路发生结构老化而导致静态参数发生变化，这些变化若无法被及时感知将影响状态估计结果的准确性，故还需将配电变压器和馈线的额定静态参数作为状态量一同估计，拓展估计范围。

（3）由于可再生能源和储能系统大量接入配电网，已不能将电源和负荷简单地等效为功率注入。需充分考虑光伏阵列、蓄电组、DC/AC变换器等元器件的影响，建立更加详细的智能配电网状态估计量测函数。

1.2 动态状态估计

实际配电网络的量测量和状态量实时变化，其中接入的间歇式DG输出功率具有明显的时序性[18]，动态状态估计算法是根据多个时间断面的量测数据，对系统进行状态估计，在利用量测方程的基础上，进一步将状态转移方程也纳入滤波算法，使得在基于量测信息进行估计的同时也能够反映状态本身的时序变化规律，带有状态跟踪与预测的功能。因此该方法可以看作是只基于某一时刻采样数据进行滤波的静态状态估计方法的延伸，具有更强的时效性且有望取得更高的估计精度，其动态空间模型可表示为

式中：xk为k时刻系统状态量，xk∈Rn×1；zk为k时刻量测量，zk∈Rm×1；f(xk)为状态转移函数；h(xk)为量测函数；wk为过程噪声，wk∈Rn×1；vk为量测噪声，vk∈Rm×1。

由于量测方程为非线性模型，动态配电网状态估计以扩展卡尔曼滤波EKF（extended Kalman filter）[19]和无迹卡尔曼滤波UKF（unscented Kalman filter）[20]为主。EKF在计算雅可比矩阵时不可避免的存在线性化误差。相比于UKF，无迹变换UT（unscented transform）近似获取的非线性变换后的统计特征，无需计算雅可比矩阵，且具有更高的滤波精度和稳定性，近些年受到研究人员的更多青睐。然而，过程噪声和量测噪声是否准确对UKF算法估计的结果好坏有着很大的影响，甚至有可能导致算法发散。目前UKF普遍采用的状态转移函数模型为Holt两参数线性平滑参数预测模型，该模型存在着较大的建模误差，而且主动配电网中负荷及DG的随机波动导致状态容易发生变化，因此过程噪声的统计参数是时变的且难以获得。文献[21]针对该问题采用基于广义鲁棒极大似然估计器的UKF算法来进行状态估计。文献[22]基于改进的次Sage-Husa法对过程噪声进行估计，通过强化新数据的作用逐渐对陈旧数据进行遗忘，该方法可一定程度上抵消未知建模的影响。文献[23]指出UKF算法中无偏噪声估计器容易导致过程协方差矩阵出现非正定性削弱算法的鲁棒性，使算法在运行过程中出现病态无法继续运行。因此，在无偏噪声估计器的基础上结合使用有偏噪声估计器来保证算法的鲁棒性，同时为了使有偏噪声估计器损失更少的校正信息对有偏噪声估计器进行一定的改进，使其既能保证算法的鲁棒性，又能保留大部分无偏噪声估计器里的协方差校正项。

动态状态估计在各种场景下的实际运用方面取得了丰富的研究成果。文献[24]利用动态状态估计算法，实时调整预测误差协方差阵，实现在配电系统存在光伏发电及电动汽车随机充放电场景下对节点电压以及相角的高精度跟踪，并在负荷突变时能够保证估计结果不失真。文献[25]采用平方根形式的UKF并结合PMU量测数据，在线路发生三相短路故障、两相接地短路故障等情况下，从故障清除时刻开始在0～10 s内进行动态状态估计，其估计过程能够快速收敛，数值稳定性好，可实现对故障状态量的快速跟踪。文献[26]针对系统量测数据出现较高比例粗差的情况，引入粗差判据，通过增强因子自动降低粗差量测量的权重，增强UKF算法的鲁棒性，确保估计结果不会在量测粗差的影响下出现较大的偏差。

随着PMU在配电网中的广泛应用，对节点电压相量、节点注入电流相量和支路电流相量能够进行数据采集，对PMU测得的节点电压相量可直接参与滤波，其量测方程与等式约束方程均为线性方程。这样复杂的非线性估计问题便转化为线性估计问题，既有利于降低算法的计算量，又能够避免非线性方程线性化后带来的累积误差，保证算法的收敛性。

2 非完备量测下的配电网状态估计

在量测系统中，1个遥测量需经过多个环节才能到达数据中心，由于数据在采集和传送过程中本身存在一定延时，而通信网络带宽的限制也会导致量测数据延时问题加剧。此外，当通信链路不稳定或终端传感器发生故障时，有可能出现数据丢包现象，一般将这类现象统称为非完备量测[27]。

2.1 量测延时

针对量测延时，静态状态估计与动态状态估计有着不同的处理方案，如图2所示。若是在静态状态估计框架下[28-29]，首先需根据历史数据评估一天中不同时间点的潮流变化情况，得到量测变化率b。同时根据每个测点的量测值传送情况，得出时延期望值d。量测延时引起的量测偏差值可表示为ΔL=db，故目标函数变为

图2 量测延时下状态估计架构Fig.2 State estimation architecture with measurement delay

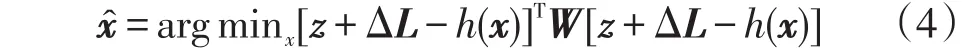
相对于静态状态估计下假设量测时滞为确定性延迟，动态状态估计可以对量测随机时滞进行更好的描述[30]。具有一步随机时滞的动态状态估计模型为

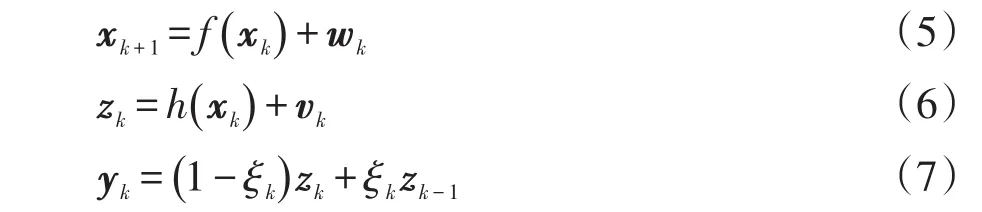
式中：zk为k时刻系统理想量测值；yk为k时刻系统实际收到的量测值。研究中一般假设ξk(k＞1)满足0或1的Bernoulli分布。在估计模型时考虑了量测值随机时滞性，使总体估计过程与传统动态状态估计算法相同，都需经过一步预测和状态校正两个步骤。不同点在于需用给定Yk条件下的后验概率密度函数p(xk|Yk)的估计取代对给定Zk条件下的后验概率密度p(xk|Zk)的估计，Yk=[y1,y2,…,yk]，Zk=[z1,z2,…,zk]分别为初始时刻到k时刻系统实际收到的量测值序列和理想量测值序列。另外根据最小均方估计准则，对具有一步延时的量测模型下的最优卡尔曼增益矩阵进行重新推导。

2.2 量测丢失

当出现量测数据丢包时，将导致配电网量测信息的冗余度降低，状态估计时可用的量测信息减少，估计精度大幅度下降，严重时甚至导致系统不可观。在量测数据概率性丢包的情况下，如何优化滤波算法保证估计精度是配电网状态估计中急需解决的问题。文献[31]利用Bernoulli分布来设计数据随机丢失环境下的滤波器结构，根据最小均方误差估计准则，推导出误差协方差矩阵的上界值，通过极小化该矩阵的迹求解最优增益矩阵并利用EKF算法进行状态估计，保证了滤波的精度及其稳定性。文献[32]从量测数据包连续丢失的角度出发，利用最接近数据丢失时刻收到的信息对丢失的量测值进行补偿，同时结合Holt双参数指数平滑和UKF方法建立数据丢包后的动态状态估计模型，使其能够克服普通动态状态估计算法在数据丢失后无法进行正确的系统预测与校正，导致估计效果变差的问题。

目前有关于量测数据延时、丢包都是针对单一状况进行单独的研究和分析。例如：在主要讨论测量数据发生延迟的估计问题时，默认数据丢包的情况不存在；在只考虑量测数据丢失的情况时，假设量测数据都在同一时刻到达。然而现实中数据延时和丢包状况相互耦合，常常是同时发生，在某个时刻估计系统没有收到相应的测量数据，既可能是测量数据发生了丢失，也可能发生了延迟。如果直接将未能按时收到的测量数据当作丢失来处理，那么估计出的状态量精度就会下降。因此，未来对估计算法进行研究改进时应同时考虑发生延迟和随机性丢失的情况，从而充分利用所掌握的信息来对配电网真实状态进行高精度的估计。

3 多源量测信息下的配电网混合状态估计

当前配电网中可用的量测数据包括RTU数据、PMU数据及AMI数据。其中，RTU数据覆盖率高，但精度低延时大；PMU测量速度快，并通过GPS对时，数据的同步性好，精度高，但目前PMU的成本处于相对较高的水平，布局较少；AMI数据精度高，但采样周期长，不能满足配电系统的实时要求。在未来很长一段时间内配电网的量测体系都会同时存在这3种量测类型，因此如何合理配置PMU，以及多种数据的有效融合问题将是研究的重点。

在多源量测环境下由于AMI采样周期较长，在相邻两次AMI量测值传到数据中心期间RTU及PMU量测数据已不同程度更新多次。为不造成数据浪费，同时提高状态估计更新频率，一般以AMI量测时刻t1作为大周期的启动时刻，t1时刻的3种量测数据在经量测变换后进行状态估计。同时，基于估计结果通过插值等方法对装有AMI的节点电压进行预测，将预测值作为t2时刻状态估计的伪测量值，最终在AMI采样间隔内得到一系列数据。状态估计结果在小周期下更新多次，直至AMI下一采样时刻。多源量测信息下的配电网状态估计框架如图3所示。

陶水旺就是被那个畜生蹬到水里的人。怪不得，那天晚上的木排老是晃晃悠悠的，他一直没离开啊。表姐脑子一下子空了，碗落在锅里，咚的一声，摔成了两瓣。

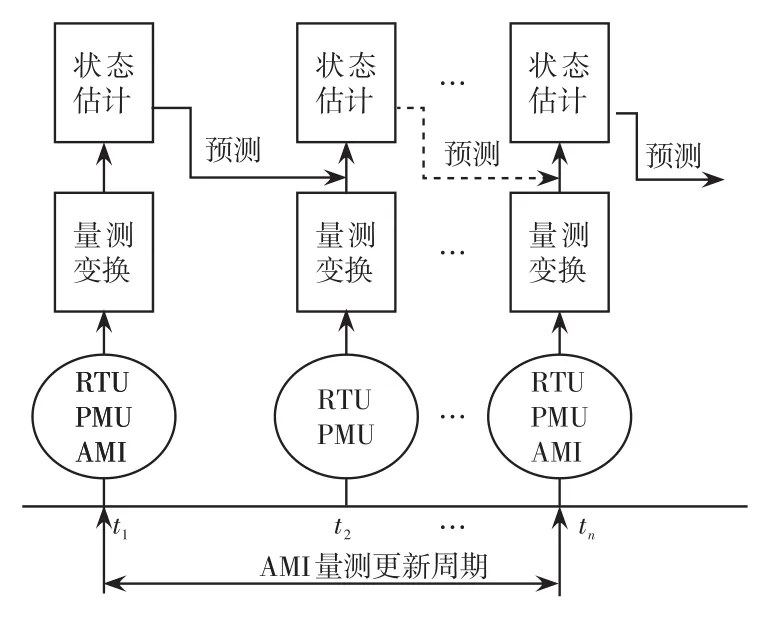
图3 多源量测信息下的配电网状态估计框架Fig.3 State estimation architecture for distribution network based on multi-source measurement information

文献[33]以状态估计最小均方误差最小为目标，以PMU数量为约束，建立了PMU优化配置模型，并采用启发式算法进行模型求解。文献[34]在计及DG出力的不确定性基础上，提出了考虑经济性及节点电压越限情况的多目标PMU最优配置算法。文献[35]从大数据挖掘的角度出发，采用改进模糊均值聚类算法对RTU数据依据相关度分区并找出各分区内最大可观测节点，在该节点上配置PMU，这些配置方法都得到了较为满意的结果，不足之处是算法计算时间较长。对于数据融合估计问题，文献[36]首先对RTU量测数据进行非线性状态估计，然后将PMU实时相量量测与已获取的估计结果共同作为量测量进行线性混合状态估计，有效减少了算法的计算时间。文献[37]重点关注了PMU和RTU数据刷新频率的差异，运用数据互相关系数法对这两种量测进行匹配，形成一套可行的数据兼容方案，但该方法由于计算复杂度过高及数据自相似，导致相似度测度的极大值不明显。文献[38]对PMU和RTU这两套数据的4种差异性进行了详细的综合分析，并分别给出了相应的解决方案，首先，将RTU的数据采集卡采用相同的采样频率并将遥测死区值设置为0以提高数据断面一致性；然后，采用多项式拟合法填补PMU时间断面下的RTU量测空缺，建立多时间标尺混合量测预处理数据集，使PMU数据得到充分利用的同时也大大缩短了状态估计的周期。文献[39]使RTU、PMU、AMI等3种量测量进行相互校验互为初值，并通过静态状态估计与动态状态估计相互配合，使算法能够较好地跟踪主动配电网的运行状态。文献[40]设计了以两个时间尺度构成的状态估计模型用来应对不同的数据刷新周期，并讨论了线性外插、线性内插法产生的中间数据对状态估计结果的不同影响。

综上，目前在混合状态估计中数据兼容性问题得到了较好的解决，使各种量测装置能够发挥其最大的作用，但是还存在以下问题。

（1）为了解决不同量测装置得到的数据成分差异的问题，现有方法是通过量测变换技术将RTU采集的量测量转换为等效节点注入电流的实部与虚部量测，以及支路电流的实部与虚部量测，或是将PMU采集的支路电流相量数据转化为等效功率量测或电压相量量测后进行状态估计。在量测变换过程中出现的传递误差会对状态估计的精度与稳定性造成影响。

（2）目前大部分混合算法中信息矩阵权重的权值大小仅仅取决于量测设备的精度，但是还应该考虑延时对数据准确性造成的影响及插值数据的精度，进而对权值进行更为合理的选取。

4 网络攻击

虚假数据注入攻击FDIA（false data injection attack）为通过篡改测量数据以破坏电网信息完整性的攻击方式[41]。在状态估计算法中常以最大标准化残差LNR（largest normalized residual）作为不良数据的检测方法，残差表达式为

当‖r‖大于阈值时表明在量测量中存在不良数据。用a=[a1,a2,…,am]T表示攻击者在量测量中注入的虚假数据，则量测数据变为zbad=z+a；虚假数据的注入引起状态变量的误差向量为c=[c1,c2,...,cn]T，估计的状态变量变为xbad=+c。此时残差表达式变为

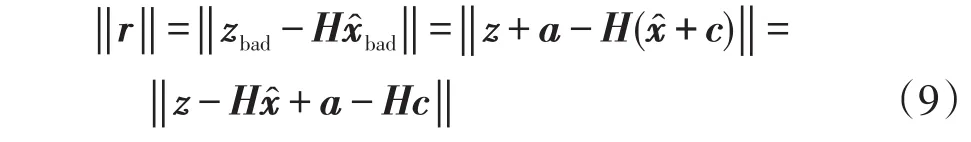
式中，H为破解通信加密后利用主成分分析法获取的量测矩阵。

当a=Hc时，有下式成立：

式中，τ为检测阈值向量。只要注入的虚假数据满足a=Hc，就可以有效躲避LNR的检验。FDIA正是利用传统状态估计算法对不良数据检测的局限性，恶意篡改量测值，使控制中心对当前电网的状态做出错误的判断进而影响电力系统的安全稳定运行。

4.1 虚假数据构建方法

从攻击者的角度出发，研究以最低的成本构建效果最好的攻击向量，目的是揭示网络攻击方的行为特征及量测系统的脆弱点。文献[42]对电网的拓扑进行数据攻击，通过修改量测值以及开关和断路器的状态使得控制中心得到错误的拓扑结构，这种攻击方式具有较高的隐蔽性不易被检测到。文献[43]提出了一种基于几何方法的盲态数据攻击方式，该方法无需提前知晓任何电网拓扑和线路导纳参数，只需利用被攻击的原始系统负荷信息，通过主成分分析法对雅可比矩阵元素进行近似估计，然后基于最小化量测量和攻击向量之间的角度进行算法设计。文献[44]构建了一种虚假数据双层攻击模型，上层攻击方在保证攻击方案不被状态估计器检测出来的条件下，使电力系统的损失最大化，下层模拟调度人员根据攻击后的估计结果进行优化调度，结果表明若攻击方具有专业的电力系统调度知识将会大大增加攻击带来的损失。文献[45]运用马尔可夫链和深度优先算法模拟计算各个断路器和分段开关受到攻击的概率，并结合攻击后的虚假数据对不同配电终端的风险值进行量化分析。

4.2 虚假数据检测辨识

由于LNR无法对恶意注入的虚假数据进行有效的检测辨识，国内外学者开始研究依据系统运行状态规律、量测量之间的时空关系、大数据挖掘等方式检测各类型的虚假数据。文献[41]提出采用非线性滤波器的迟滞特性对虚假数据注入攻击进行辨识，通过欧式距离及余弦相似度比较UKF算法与WLS估计值的相似度在线辨识恶意数据。配电网的量测数据之间具有时间和空间相关性，当有恶意数据注入时相关性可能会有所偏移，文献[46]通过离散小波变换和深度神经网络来捕捉这种不一致进而实现对恶意注入数据的检测。文献[47]从模糊聚类的角度出发，将监督学习、半监督学习、决策级和特征级进行融合运用对攻击行为进行分类检测。

虚假数据攻击与检测辨识本质上是一个动态博弈的过程，若借鉴经济学中的博弈论思想，对于配电网络攻击方式与检测手段的研究将会有更深层次的突破。

4.3 网络攻击下的配电网状态估计

在攻击者对终端数据采集设备或通信网络进行虚假数据注入攻击后，量测量被传送到数据中心，状态估计器利用夹着虚假数据的量测量进行首次状态估计，同时利用机器学习算法进行虚假数据存在性初步检测，判断所有量测值中是否存在虚假数据。若检测出系统存在虚假数据，则将所有量测数据发送到分类器进行虚假数据辨识，确定存在虚假数据的量测值并将这些数据从普通量测值中剥离。为保证系统可观，需运用主成分分析等方法从剩余正常数据中提取数据特征并结合历史数据生成与剔除的数据真实值尽可能一样的数据，加入到之前剔除了虚假数据的剩余量测中，合成补全数据，最后将补全的数据再次送入状态估计器中进行二次状态估计，对原来受到虚假数据影响的估计结果进行修正，从而排除了虚假数据的恶意干扰。网络攻击下配电网状态估计框架如图4所示。

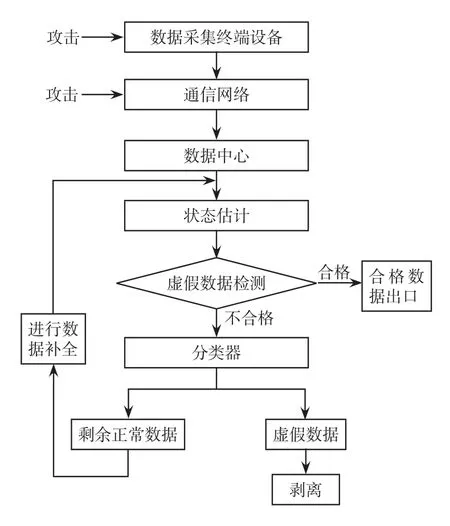
图4 网络攻击下配电网状态估计框架Fig.4 State estimation architecture for distribution network under cyber attack

5 结语与展望

本文首先介绍了配电网状态估计主要算法，指出算法中应该注意的关键点；其次，结合国内外发表的论文对非完备量测、多源量测信息环境下的状态估计技术难点及发展情况进行详尽的阐述；最后，从攻击方法和辨识策略两个角度对虚假数据注入攻击的研究现状进行概述。

尽管配电网状态估计近几年已取得了较为丰富的研究成果，但是电力电子装备及新型量测装置在配电网高比例的运用，智能配电网状态估计的研究还需重点关注以下几个方面。

（1）DG并网方式主要有同步发电机并网、异步发电机并网及电力电子异步并网，不同的并网方式和控制策略会导致配电网三相不平衡及缺相情况严重化。同时，基于电压源型换流器的柔性直流技术也越来越多的运用到交流配电网中，形成了交直流混合配电网[48]，因此状态估计常用到的导纳矩阵很难对当前配网进行完整的描述。针对该问题，文献[49]提出一种基于二次约束二次估计的配电网状态估计方法。该方法针对接入配电网的多种DG或储能系统，在直角坐标系下，根据设备模型直接生成数学上抽象的含二次等式约束及二次量测方程的状态估计模型，不需要导纳矩阵，然后再用成熟的估计算法进行求解。将状态估计问题描述为数学抽象估计模型是应对配电网拓扑结构日趋复杂的有效方法，未来值得更为深入的研究。

（2）现有的伪测量构建方式大致分为不确定性概率预测和确定性的点值预测两类。概率性预测方法为首先根据大量的负荷以及DG历史统计数据获取概率密度函数，然后利用高斯混合模型对DG和负荷的不同概率密度函数进行统一表达，以此给出所有可能出现值及其概率。点值预测法通过人工智能AI（Artificial Intelligence）预测技术对DG及负荷的大量历史数据进行高效训练，以此获得节点注入功率伪量测值。但实际电网中大多数DG出力的完整概率密度函数难以获取，而通过AI预测出的伪量测值准确度不高，并且电动汽车即插即用的特点进一步加大了预测的难度。在仿射数学中，不确定信息由有限个噪声元线性叠加而成，噪声元取值区间为[-1，1]，每个噪声元系数能够体现其所对应的不确定量大小。仿射数学在表达不确定信息上具有简单性且可以表示各不确定变量之间的相互依赖关系，体现DG出力的时空关联特征。因此，可利用仿射数对节点注入功率伪量测以及支路功率和电流幅值实时量测进行合理的仿射区间建模，再通过线性规划等方法进行求解得到状态区间的最优估计值。未来可参照潮流计算，采用仿射数学表达分布式电源出力不确定性的方法[50-51]，研究基于仿射数学的配电网状态估计算法。

（3）PMU在配电网中广泛应用加快了状态估计的更新频率，在提高状态估计结果精度的同时，也给总调中心带来了更为繁重的计算负担与存储压力，导致数值的稳定性下降加剧计算过程中的病态问题的出现。分布式状态估计按一定原则划分区域，将分布式信号处理理论与电力系统特点相结合，分块处理系统的量测数据，既可减少通信网络的拥堵和时延，又可避免繁杂的海量数据集中式处理，为多源量测环境下状态估计提供一个更为高效的实现手段以降低计算的复杂度、保证数值的稳定性和提高估计器性能。因此，未来在开发更加高效的状态估计算法的同时，可借鉴输电网研究分布式状态估计技术[52]。