增强并网逆变器对弱电网适应能力的控制策略

（四川大学电气工程学院，四川 成都 610065）

为了减少温室气体排放和对化石能源的依赖，新能源得到了广泛发展和应用。然而随着大量新能源设备和较长输电线的引入，使得电网的感性阻抗变得不可忽略，电网越来越呈现弱电网特性[1-3]，并且电网阻抗的存在将导致滤波器谐振频率向低频区域移动，这会影响电流控制系统的鲁棒性。在已有的文献中，有很多关于弱电网运行情况下抑制谐振并改进电流控制稳定性的方法介绍以及讨论。

文献[4]提到了一种对前馈通道的选频处理办法，可以有效减少电网阻抗在谐振频率段的幅值，增强并网逆变器对弱电网的适应能力。文献[5]提出了一种基于电压型阻抗适配器的控制策略，通过虚拟较小的谐波阻抗，对公共耦合点进行阻抗重塑，继而降低谐波。文献[6]基于同步频率谐振现象的产生原理，提出基于暂态虚拟电阻的阻尼控制策略来解决谐振问题，但其关于弱电网条件下电压前馈控制对并网逆变器的影响机理并没有给出详细的解释。文献[7]提出通过减少前馈增益来提高并网逆变器稳定裕度，但是电压前馈增益的减少会使逆变器输出阻抗减小，不利于并网电流谐波的抑制。文献[8]从并网逆变器锁相环的静态稳定性角度出发，求出保持并网逆变器稳定的极限功率，但是作者没有考虑电流内环响应时间，因此理论结果与实际情况有一定差别。文献[9]提出了一种基于瞬时无功功率理论的新型并网逆变器控制策略，作者通过采用直流侧电压控制方式稳定逆变器直流侧电压进而降低并网电流谐波。文献[10]对锁相环进行了改进，利用谐波消除模块消除电网电压中的谐波分量，有效地降低了谐波对输出相角的影响，改善了并网电流的输出波形。文献[11]讨论了通过电流电容反馈进而实现谐振的抑制，但这种传统的单一阻尼控制策略并没有得到很理想的并网电流波形，存在一定的谐波失真。

作为可再生能源系统与电网之间的重要连接通道，并网逆变器一直是学者们研究弱电网的入手点，为了抑制并网逆变器启动时的冲击电流以及电网电压畸变对系统带来的不利影响，电网电压前馈控制策略被广泛使用在并网逆变器上，旨在降低并网电流谐波，提高电能质量[12-16]。然而额外的正反馈通路被引入到弱电网中，一旦设计不合理必然会给系统带来低次谐波污染，同时也会导致相位裕度减少，进而影响稳定性[17-21]。

针对电压前馈控制的局限性，本文提出了一种新型的基于超前相位补偿的电压前馈控制策略，即在控制环节中加入相位补偿单元，提高系统在谐振频率处的稳定裕度。该策略既保留了电压前馈控制的优点，又降低电网阻抗对系统鲁棒性造成的不利影响，并通过仿真证明了此控制策略的有效性。

1 并网逆变器输出阻抗建模

本文的研究对象是LCL单相并网逆变器接入弱电网系统。

图1给出了两台单相LCL逆变器并联的系统模型，L1n为逆变器直流侧电感，L2n为逆变器电网侧电感，Lg为感性电网阻抗。为方便下文利用阻抗法分析输出阻抗的稳定裕度，可建立LCL单相逆变器并联系统的诺顿等效电路，如图2所示。图2中的Gn为不同并网逆变器的输出电流开环增益，Zn为不同并网逆变器对应的输出阻抗。

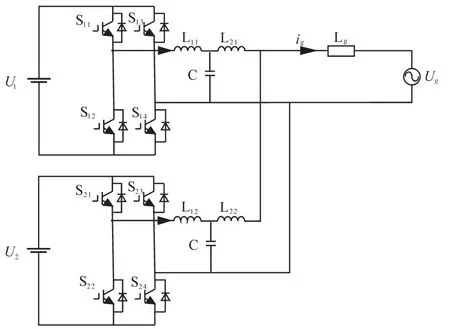
图1 逆变器并联运行系统拓扑Fig.1 Topology of inverter parallel operation system

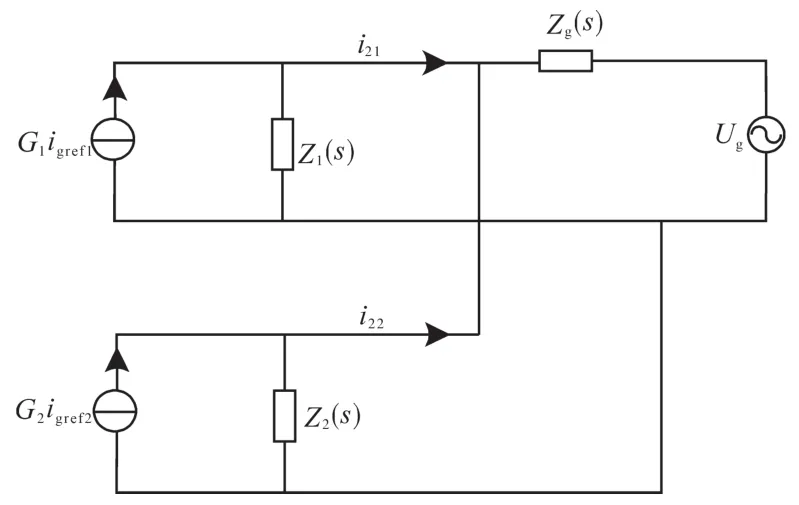
图2 逆变器并联系统等效模型Fig.2 Equivalent model of inverter parallel system

根据叠加定理，在已知并网电压Ug和参考电流的情况下，可以用闭环传递函数矩阵来表示并网电流，如下式：

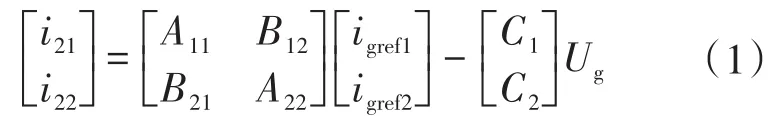
式中：A11，A22为自身逆变器的参考电流到并网电流的传递函数；B12，B21为其他逆变器的参考电流到并网电流的传递函数；C1，C2为电网电压到并网电流的传递函数。

本文的研究重点为抑制谐振及提高系统稳定裕度，所以此处可将式（1）进行简化，即设定并联的两台逆变器器件相同，且具有相同的控制参数与特性，再结合逆变器并网的诺顿等效电路得：

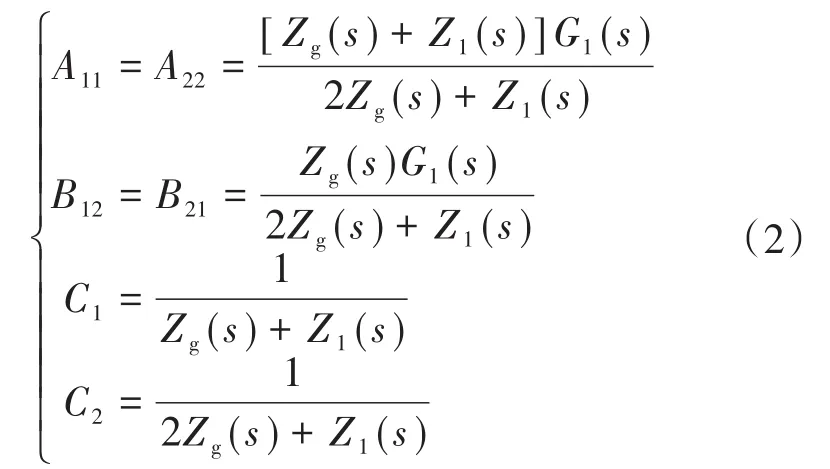
在理想条件下，即忽略电网阻抗对系统的影响时，B12=B21=0，此时两台并联运行的逆变器可以相互解耦，只要单台并网逆变器正常工作，谐振现象就不会发生。然而现实中随着大量新能源设备和较长输电线的引入，使得电网阻抗变得不可忽略，并且在加入电网阻抗后，谐振频率也会降低。

考虑到实际电网阻抗Zg（s）包含阻性分量和感性分量两部分，而阻性部分可以对控制系统起到阻尼作用，增强系统稳定性；并且将电网阻抗看作纯感性时，仍能保证不存在右半平面零极点，确保了电网侧稳定条件不被破坏。所以为了更具有说服力，本文考虑最坏的情况，即认为电网阻抗是纯感性元件。

2 弱电网下前馈控制对系统鲁棒性的影响

2.1 电压前馈控制对谐振的抑制作用

图3给出加入有源阻尼的LCL并网逆变器双环控制结构图。

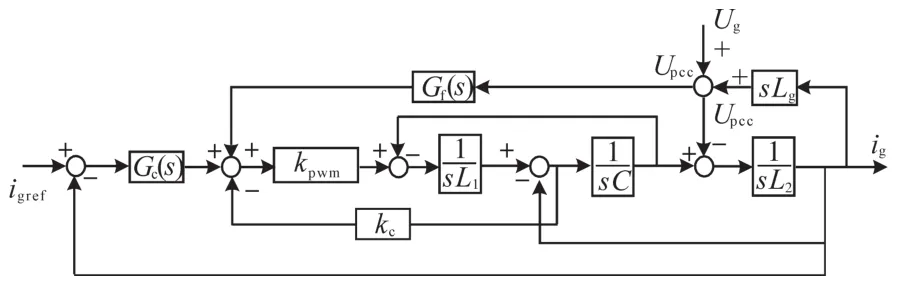
图3 弱电网下的电流双环控制结构Fig.3 Current double-loop control structure in weak grid

图3中，Gf（s）为前馈环节，Upcc为公共耦合点的电压，kc为电容电流反馈系数，Gc（s）为电流调节器，此处采用PI调节，即

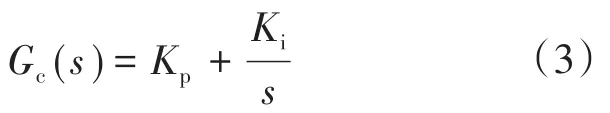
式中：Kp为比例系数，Ki为积分系数，两者的取值大小可根据文献[22]进行计算。

此时，参考电流到电网电流的开环传递函数如下：

其中

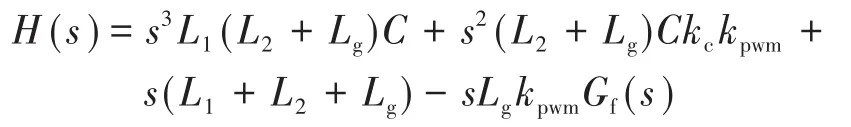
前馈回路可以抑制谐振，然而前馈回路是正反馈，所以当前馈增益过大时也会导致相位的变化，因此必须综合考虑前馈增益的取值。

图4给出了前馈增益K变化时对控制系统稳定性的影响，通过与K=0时刻的伯德图对比，发现引入公共耦合点电压前馈，必然可以减小谐振，Gf（s）=K=1时，谐振基本被抑制。

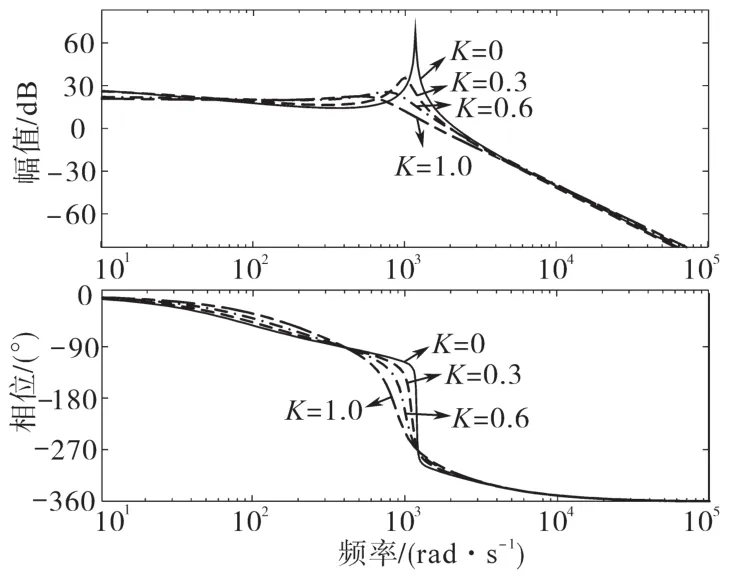
图4 不同前馈增益对应的伯德图Fig.4 Bode diagram corresponding to different feedforward gains

2.2 弱电网采用电压前馈出现的问题

从图4可以看出，随着增益K增加，相位滞后也越来越严重。针对这一现象，本节将站在阻抗法的角度来分析。在考虑电网阻抗时，Upcc到电网电流ig的开环传递为

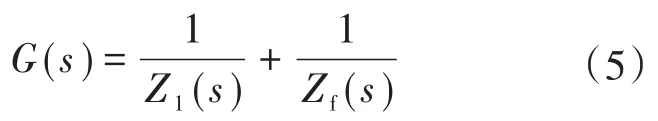
其中

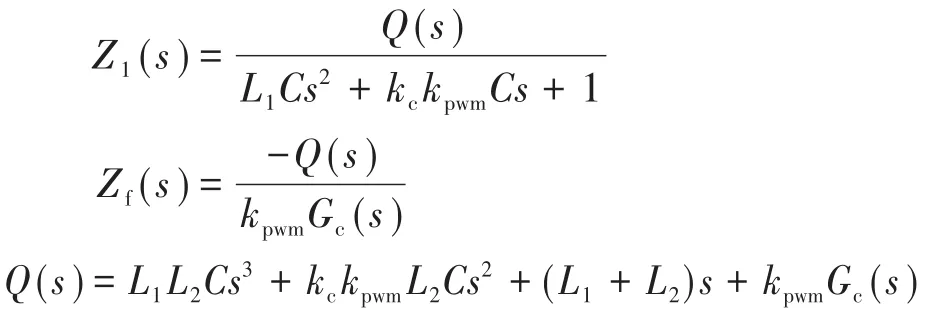
式中：Z1（s）为不加前馈控制时，并网逆变器的输出阻抗；Zf（s）为电压前馈控制的等效阻抗。

本文采用阻抗分析法，将并网逆变器等效为电流源，得到系统的诺顿等效电路，如图5所示。

图5 并网逆变器的诺顿等效电路Fig.5 Norton equivalent circuit of grid-connected inverter

并网总电流可表示如下：

式中：G1igref1为单台逆变器等效电流源。

两台逆变器并联接入弱电网，因此Zg（s）为2倍的电网阻抗。要确保并网逆变器对弱电网有适应能力，首先，需要满足电网侧稳定，而本文研究的情况是电网阻抗为纯电感，零极点不会出现在右平面；其次，电网阻抗与逆变器输出阻抗之比需满足奈奎斯特判据，如果电网阻抗和逆变器输出阻抗在幅频特性曲线上无交点，说明系统稳定。若存在交点，则需相角裕度大于0°，相角裕度表达式为

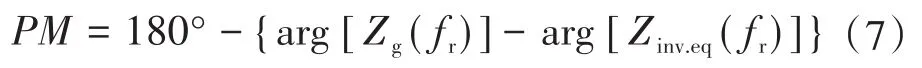
式中：fr为交点处的谐振频率。

电网阻抗的相位为90°，因此要保证交点处相角裕度大于0°，逆变器等效的输出阻抗相位要大于-90°。图6给出加入电压前馈环节前后的逆变器输出阻抗伯德图。

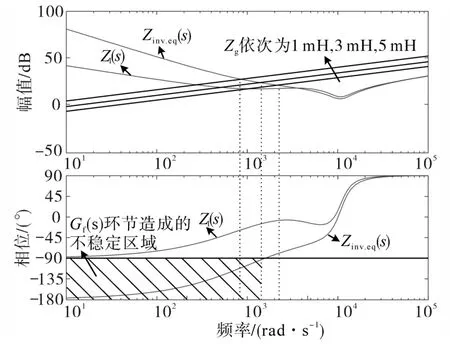
图6 电压前馈对逆变器输出阻抗的影响Fig.6 Effect of voltage feedforward on inverter output impedance

通过将Z1（s）与Zinv.eq（s）的伯德图对比，发现系统引入电压前馈回路时，相角裕度大幅降低，在低频区，arg[Zinv.eq]＜-90°，即当电网阻抗与逆变器等效输出阻抗的交截点频率出现在低频区时，系统相角裕度不足，容易引发谐振，从而使系统失稳。并且随着电网阻抗Zg增大，相角裕度变得更小。

2.3 加入相位超前补偿环节的前馈控制策略

提高逆变器等效输出阻抗的相角裕度可以避免并网逆变器与电网阻抗发生谐振，因此本文考虑在电压前馈控制的基础上加入相位超前补偿环节，如图7所示。

图7 加入相位补偿环节后的电流双环控制结构Fig.7 Current double-loop control structure with phase compensation

图7中，补偿函数Gi（s）表示为

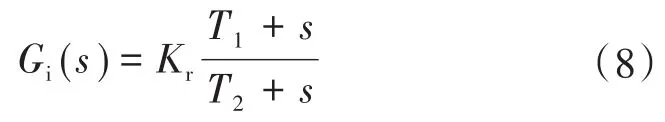
式中：Kr为常数；T1，T2为相角补偿系数。

调整相角补偿系数，使得补偿函数Gi（s）的最大相角处频率与逆变器阻抗和电网阻抗交截点处的频率相等，从而得到最优补偿效果。Gi（s）在交截点处的补偿值为

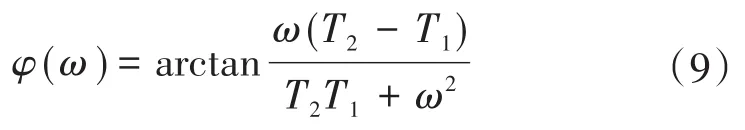
令dφ（ω）/dω=0，此时补偿效果最优，此时补偿环节最大处的频率为

联立式（9）、式（10）得最大相位超前补偿角公式如下式：

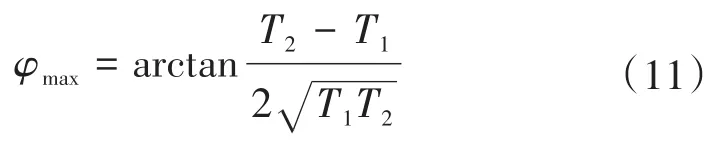
为了不改变阻抗幅值在补偿角频率处的大小，补偿函数中的Kr取值要满足Gi（ωmax）=1。此时，其可以表示为

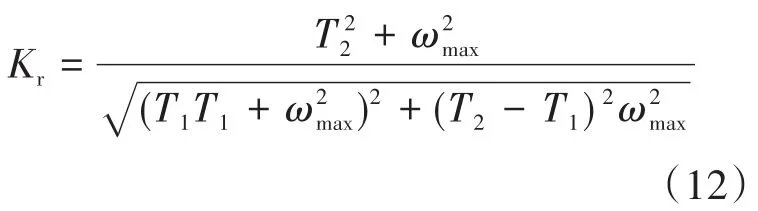
加入相位超前补偿环节后，参考电流到并网电流的传递函数表示为

Upcc到电网电流ig的开环传递函数可用下式来表示：

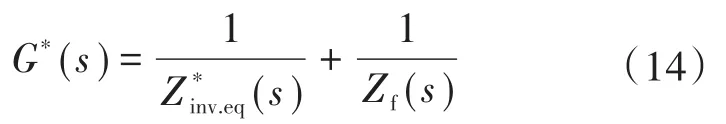
计算得出加入补偿环节后，逆变器等效输出阻抗为

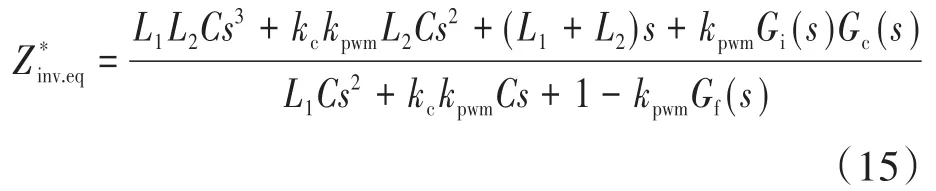
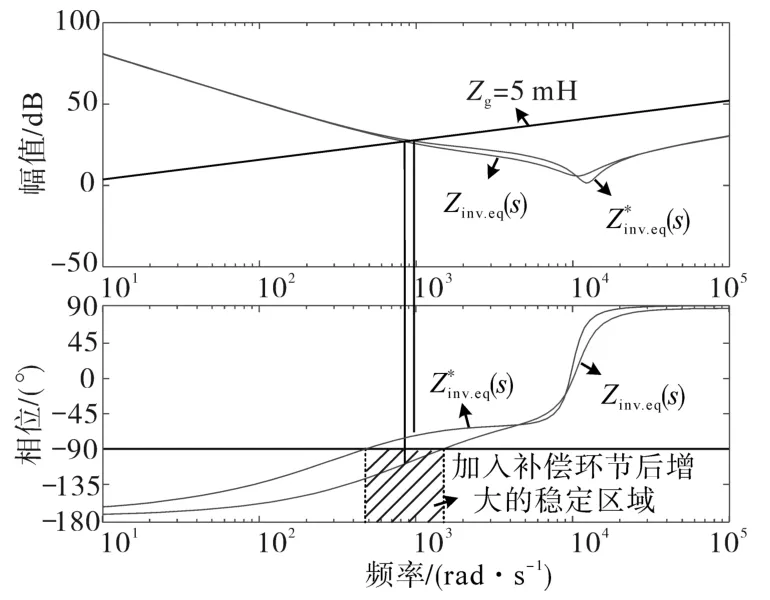
图8 相位补偿对逆变器输出阻抗的影响Fig.8 Influence of phase compensation on inverter output impedance

3 仿真验证

为了验证本文所提控制策略的有效性，在Matlab搭建两台相同规格的LCL单相并网逆变器的仿真模型，通过测试不同电网阻抗下的并网电流谐波失真率，分析并网逆变器对弱电网的适应能力。考虑到两台逆变器并联，因此电网阻抗扩大2倍。本文以1号逆变器的并网电流作为结果进行分析。针对时变的电网阻抗（Zg（s）=0～5 mH），逆变器的各元件规格以及控制参数如下：直流电压源Vdc＝800 V，电网电压Vg＝380 V，滤波电感L1＝0.7 mH，滤波电感L2＝0.3 mH，滤波电容Cf＝20 μF，电压前馈系数Gf＝1，相补偿系数T1＝7 850，相角补偿系数T2＝16 500，补偿比例系数Kr＝1.68，电容电流反馈系数kc＝0.027，调节器参数Kp/Ki＝0.025/33。

图9给出不加入补偿环节时，不同电网阻抗所对应的并网电流仿真波形。随着电网阻抗增大，系统稳定性降低，谐振谐波现象严重。当电网阻抗Zg分别为3mH，5mH时，谐波失真率THD分别为6.31%，9.08%，不满足并网要求的5%以下。

图9 加入相位补偿前的并网电流波形图Fig.9 Waveforms of grid-connected current before adding phase compensation

图10给出了加入相位超前补偿环节后的并网电流波形。通过与图9的对比反映出，采用本文所提的相位超前补偿策略，提高了并网电流质量，增强了LCL并网逆变器对弱电网的适应能力，谐波失真率THD分别为1.98%，3.93%，谐波现象得到明显改善，满足并网要求的5%以下。

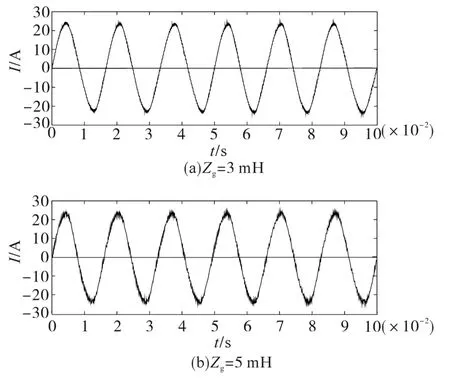
图10 加入相位补偿后的并网电流波形图Fig.10 Waveforms of grid-connected current after adding phase compensation

为了更直观地反映本文所提相位超前补偿控制策略的有效性，在弱电网系统（Zg=5mH）处于谐波谐振的状态下，t=0.05 s时加入相位补偿环节，并网电流如图11所示。通过对比可以看出，加入相位超前补偿后，由于相角裕度增大，谐波谐振现象显著减弱。

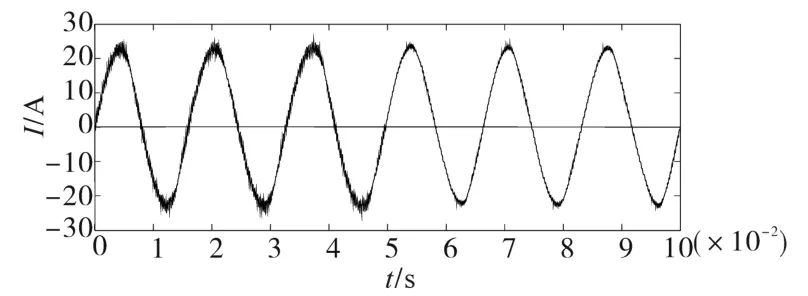
图11 相位补偿策略对并网电流的影响Fig.11 Effect of phase compensation strategy on grid-connected current

仿真结果也论证了加入相位超前补偿环节后，当电网阻抗Zg（s）在0～5 mH的范围内变化时，系统始终具有良好的稳定性。

4 结论

本文分析了电压前馈控制对并网逆变器系统稳定性的影响。分析表明，传统的电压比例前馈虽然可以抑制谐振，但也会导致逆变器输出阻抗的相角裕度减小，从而降低并网逆变器对弱电网的适应能力。针对这种局限性，本文研究出一种新的基于电压前馈控制的相位超前补偿方法，既完整保留了电压前馈控制的优点，又提高了并网逆变器的相角裕度，使系统对电网阻抗具有较强的鲁棒性。仿真结果验证了所提相位补偿方法的有效性。