基于阻抗在线观测的光伏逆变器控制策略研究

李春来 ，苑舜

（1.沈阳工业大学电气工程学院，辽宁 沈阳 110870；2.国网青海省电力公司清洁能源发展研究院，青海 西宁 810008）

随着分布式发电装置的并网容量逐步增大，分布式发电装置不能再作为简单的电源向电网注入有功功率，还应该承担维持电网稳定性的重担[1]。然而，以光伏发电为例，目前并网运行的光伏逆变器并不参与电网电压控制，始终运行最大功率跟踪算法，尽全力将太阳的辐射能量转化为电能注入电网。白天日照充分，电力负荷较轻的情况下，电网电压会升高；相对地，夜间没有日照，电力负荷较重的情况下，电网电压会降低。

电网电压升高会造成负载发生过电压故障，造成严重的后果，需要通过恰当的手段排除故障或预防故障发生。目前，普遍采用的是排除故障的做法。采用过电压保护装置，一旦电网电压升高超过保护阈值，则切断与之连接的光伏逆变器。根据相关的电网规范[2]，当电网电压高于额定值的110%的时间超过10 min，光伏逆变器就必须脱离电网。尽管采取这样的做法能够有效地排除过电压故障，但是，从经济性的角度考虑，无论是发生过电压故障还是切断光伏逆变器，都是应该避免的情况。也就是说，当光照充足而电力负荷较轻，就会发生以下两种情况：1）光伏逆变器持续向电网注入能量，电网电压将不断升高，持续升高到超出额定值，进而烧毁负载；2）直接将光伏逆变器从电网中脱离，所有的光伏能量都被浪费掉，或者就地消耗掉。可以清楚地看到，以上任何一种情况都不是优秀的解决方案。

预防故障发生的解决方案是让光伏逆变器参与到电网电压的控制中，根据电网电压控制光伏逆变器的输出。当电网电压与额定值发生偏移时，光伏逆变器主动调节注入电网的有功功率和无功功率，控制电网电压返回额定值范围[3-4]。

众所周知，在阻性电网中，电网电压主要受有功功率影响；在感性电网中，电网电压主要受无功功率影响。然而，多数电网同时具备阻性和感性，也就是说，光伏逆变器输出的有功功率和无功功率都影响电网电压的控制效果，即电网电压受到电网阻抗的阻抗比R/X的影响[5-7]。

由于电网电压受电网阻抗比的影响，可以预先测量出电网的阻抗比，输入到控制策略中。然而，电网阻抗比并不是固定的，随着负载的接入和切出、电网拓扑的改变，电网阻抗比都会发生变化，特别是在低压电网中，电网阻抗比的变化范围可以非常大。因此，需要对电网阻抗进行在线观测。现有的观测方法可从不同的角度进行分类，分为在线观测和离线观测、主动观测和被动观测、暂态观测和稳态观测。相比较而言，主动的稳态在线监测能够以更经济的方式获得更准确的结果。特别地，向电网按需注入1.5次谐波的主动谐波注入稳态电网阻抗观测方法被证明是兼顾了准确性和有效性的电网阻抗在线观测方法[8]。

本文提出一种光伏逆变器的电网电压控制策略。其中，在线观测电网阻抗，根据阻抗比在线观测值动态地调整光伏逆变器注入电网的有功功率指令和无功功率指令，达到稳定电网电压的效果。本文的内容组织如下：第1节介绍本文的研究对象——光伏发电系统；第2节推导出通过控制有功功率和无功功率实现的光伏逆变器电压控制策略；第3节研究光伏并网逆变器的有功功率和无功功率的反馈控制；第4节研究电网阻抗比的在线观测；第5节研究光伏逆变器的电网电压控制；第6节通过实验描述所提控制策略的实际效果。

1 光伏发电系统

本文所研究的光伏发电系统如图1所示。系统包括光伏电池板，实现最大功率跟踪的能量收集变流器以及光伏逆变器（包括三相全桥开关网络和并网滤波器）。光伏逆变器的输出功率取决于光照和能量收集变流器对应的最大功率跟踪点[9]。光伏逆变器通过控制注入电网的电流实现对其直流电压的控制。控制策略平衡了注入直流母线的直流电能和从直流母线抽出、注入电网的交流电能。因此，注入电网的有功功率由能量收集变流器所收集到的能量所决定。

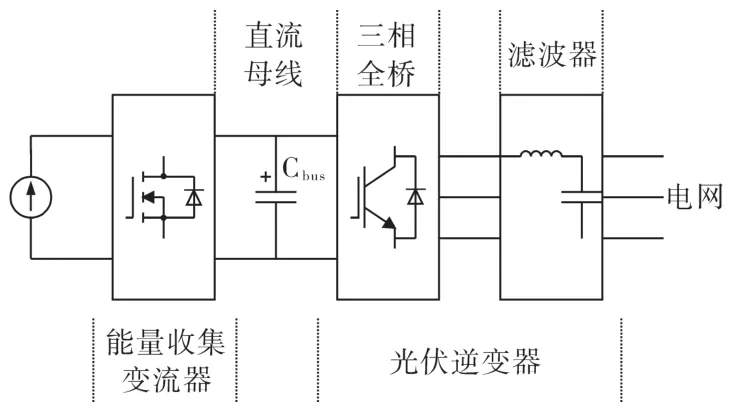
图1 光伏发电系统示意图Fig.1 PV distributed generation system diagram

本文所研究的控制策略不仅对光伏逆变器注入电网的有功功率和无功功率进行控制，与此同时，光伏逆变器主动对电网阻抗比进行在线观测，根据阻抗比观测值，动态设定光伏逆变器注入电网的有功功率指令和无功功率指令。

2 电网电压和频率的控制

阻性电网中，电网电压受有功功率控制；感性电网中，电网电压受无功功率控制。对于电网频率的控制则恰好相反：阻性电网中，电网频率受无功功率控制；感性电网中，电网频率受有功功率控制。普遍采用的电网电压和频率的下垂控制方程[10]如下：

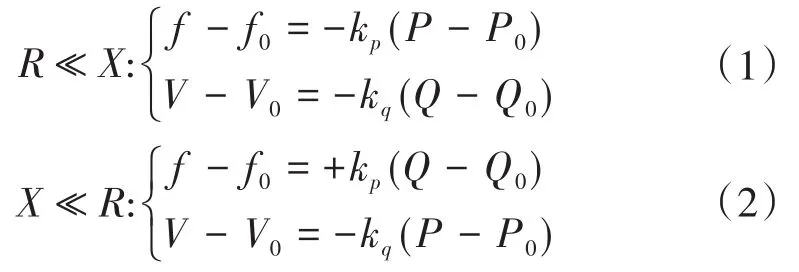
式中：kp为有功功率的下垂控制参数；kq为无功功率的下垂控制参数；V为电网电压实时的幅值；f为电网电压实时的频率；P为光伏逆变器注入电网的有功功率；Q为光伏逆变器注入电网的无功功率；R为电网阻抗中的电阻分量；X为电网阻抗中的电抗分量；V0，f0分别为电网电压幅值和频率的额定值；P0为能量收集变流器在最大功率跟踪点所对应的有功功率；Q0为无功功率的参考值。

以阻性电网为例，电压差值引出的结果是输出有功功率成比例的变化。

正常情况下，光伏逆变器只作发电之用，它尽全力将收集到的太阳能全部转化为电能，注入电网。因此，光伏逆变器的有功功率等于P0，而Q0等于0。

对式（1）和式（2）进行扩展，可以得到电网阻抗包含电阻和电抗的混合电网中的下垂控制方程[10]如下所示：

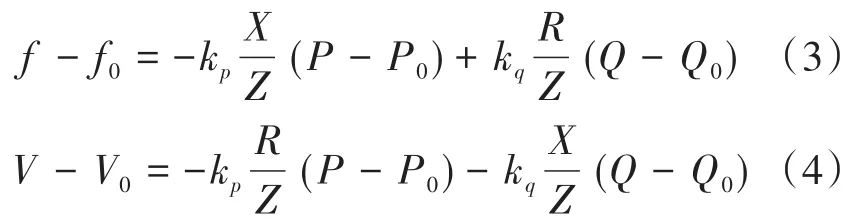
电网电压的幅值和频率能够简单地实时测量，同时，注入电网的有功功率和无功功率也能通过光伏逆变器进行控制，这样一来，式（3）和式（4）可以改写为

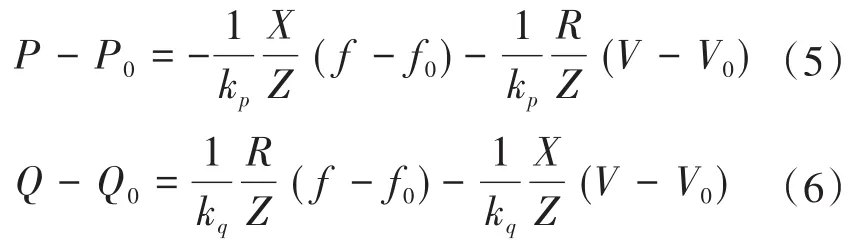
所得到的就是光伏逆变器在电网阻抗包含电阻和电抗的混合电网中的下垂控制方程。当电网电压与额定值发生偏差时，可根据式（5）和式（6）对光伏逆变器注入电网的有功功率和无功功率分别进行控制。

在光伏逆变器的实际使用中，式（5）和式（6）可以做出一些近似的简化和调整，以及一些特定的说明。

第1，频率偏离可以忽略。实际应用中，由于容量较小，光伏逆变器无法对电网频率产生影响。电网电压幅值是一个本地参数，电力系统中的每个节点都有本地的电压幅值。不同于电网电压幅值，电网频率是一个全局参数，主要由大容量的发电机组决定。因此，在本文的研究中，光伏逆变器跟随电网频率运行，不进行频率补偿。

第2，观测电网阻抗的阻抗比R/X即可。由前文的推导可知，为了达到控制电网电压的目的，需要获得电网阻抗中的电阻值R和电抗值X。尽管R和X分别单独出现在式（5）和式（6）中，但是并不需要分别观测R和X。观测阻抗比R/X就能满足光伏逆变器完成有功功率和无功功率的控制。令α=R/X，则可以得到：

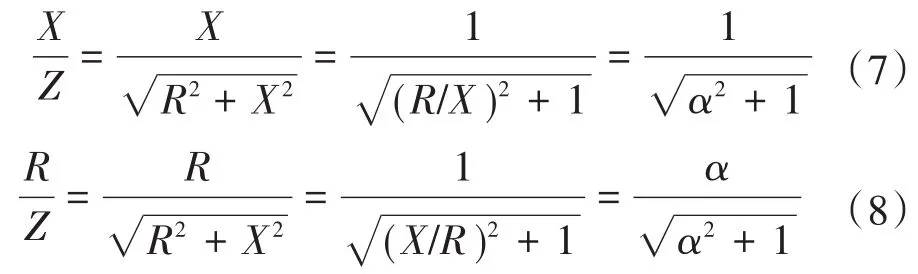
把式（7）和式（8）代入到式（5）和式（6）中，同时忽略频率偏离，即可得到以阻抗比形式描述的光伏逆变器有功功率的下垂控制方程和无功功率的下垂控制方程：

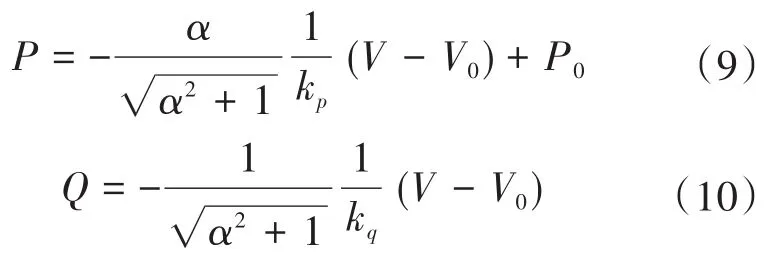
第3，参数时效性的说明。电压幅值V是实时观测结果，它按照模数转换器ADC的采样周期进行更新。最大功率点处的有功功率P0随着光照的变化而变换，考虑到云对光伏电池板的遮盖，P0的变化也在若干s的级别。电网阻抗的阻抗比按照阻抗观测器的更新周期进行更新，稳定起见，也不需要太快，同样在若干s的级别。

3 有功功率和无功功率的控制

获得电网电压偏离额定值的绝对数值后，根据前文所推导出的下垂控制方程可得到光伏逆变器注入电网的有功功率指令值和无功功率指令值，再经过反馈控制，即可达到控制电网电压的目的。本节着重描述有功功率和无功功率的反馈控制策略。

光伏逆变器的控制在d-q同步旋转坐标系下实现，此坐标系与公共连接点电压同步，因此，公共连接点的电压幅值，即前文中的V，等于旋转变换的输出 Vd，而 Vq等于0。

在三相平衡系统中，光伏逆变器注入电网的瞬时无功功率为

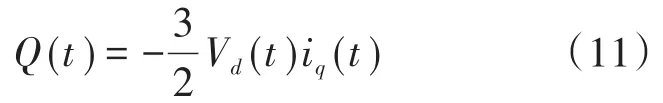
根据式（11），无功功率的控制可以通过控制q轴瞬时电流实现。

将式（11）代入式（10）中可以得到：

根据式（12），由电压幅值的偏离可以得到光伏逆变器的q轴电流参考值。

光伏逆变器不仅能够注入无功功率，还可以吸收无功功率。也就是说，通过控制注入电网的无功功率的极性和大小，光伏逆变器既可以提高公共连接点处的电压幅值，也可以降低公共连接点处的电压幅值，从而彻底实现电网电压控制。

如前文所述，光伏逆变器通过控制流入直流母线的直流能量和流出直流母线、注入电网的交流能量的平衡，从而维持直流母线电压稳定。因此，光伏逆变器输出的有功功率每时每刻都等于能量收集变流器的最大功率跟踪点的功率P0。然而，能量收集变流器不是必须工作在最大功率点。在能量收集变流器和光伏逆变器之间进行通信，根据式（9）设定能量收集变流器的功率点，注明时间变量，可以得到有功功率的指令值如下式所示：

最大功率跟踪点的有功功率P0是光伏逆变器所能注入电网的最大有功功率，光伏逆变器只能从P0向小调整，因此，只有电网电压发生的过电压才能够被纠正。当电网发生欠电压故障，且根据式（13）得到的有功功率指令值大于P0，此时光伏逆变器的有功功率指令值饱和，即等于P0。

电网欠压故障早在分布式发电兴起前就已经出现，并且，通过负载侧的无功功率补偿，得到了妥善的解决。光伏逆变器也可以提供无功功率补偿，所以，欠电压故障不是当下的主要问题。随着越来越多的分布式发电电源接入电网，它们对电网的影响显著增强，因此，在分布式发电得到充分发展的今天，过电压故障发生的概率远高于欠电压故障，也更为重要。

4 阻抗比的在线观测

在电网电压的下垂控制中，阻抗比R/X是一个重要的参数。高压输电系统中，阻抗比大约为0.3，中压电网中，阻抗比大约为0.8。然而，在低压配电系统中，阻抗比范围非常大，在2～8之间变化。

由于阻抗比在下垂控制中的重要性，电网阻抗的观测方法得到了广泛的研究。现有的观测方法可以从不同的角度进行分类：1）离线观测和在线观测。离线观测需要首先存储所有的采样信号，在线观测在接收到新的测量值的同时进行观测结果的更新；2）主动观测和被动观测。主动观测控制光伏逆变器向电网注入特定的扰动进行观测，被动观测则只是观测电网本身；3）暂态观测和稳态观测。暂态观测根据暂态特性的测量值进行观测，稳态观测则通过观测电网信号的稳态结果获得电网的阻抗比。

常见的观测方法有以下3种：1）基于扩展卡尔曼滤波器的无源观测方法对电网友好[11]，然而受限于巨大的计算量；2）采用有源滤波的LCL滤波器的在线观测方法[12]只能观测电网阻抗中的电抗，而且它需要额外的电流传感器；3）在具体的实施中，最容易实施的方法是非特征电流注入法，它既不需要在光伏逆变器中添加额外的元件，也不需要光伏逆变器测量新的信号[8]。这种方法通过光伏逆变器向电网注入一个谐波电流，对电网电压和电网电流进行离散傅里叶分析（discrete Fourier transformation，DFT）即可得到电网阻抗的观测值。本文采用非特征电流注入法对电网阻抗进行在线观测。采用DFT进行阻抗的在线观测可以有效地防止谐波成分对阻抗在线观测结果的影响。

首先需要明确，在线观测的目的是获得电网基波频率下的电网阻抗比，也就是50 Hz处的电网阻抗比。

对于每一次谐波，都可以得到相应的电网阻抗。对第h次谐波，它的阻抗为

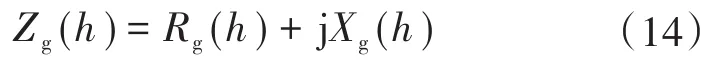
第h次谐波的阻抗可以根据下式得出：

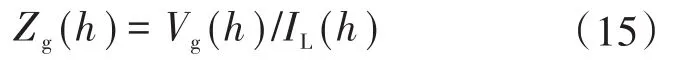
对特定的谐波，所计算出的电网阻抗并不等于50 Hz基波频率处的电网阻抗。电网阻抗中的电感表示为Xg（h）=ω（h）L（h）。由于集肤效应和邻近效应，参数Rg（h）和L（h）都与谐波次数h有关。使用h次谐波观测电网阻抗，需要用到近似计算：

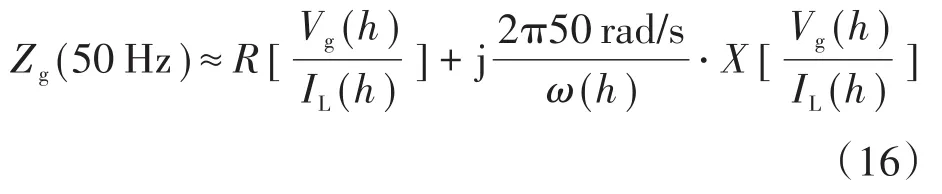
其中，Vg（h）和IL（h）通过DFT计算得出。

所注入的谐波频率应该尽可能接近基波频率，从而使得式（16）近似有效。与此同时，谐波对电网的影响也应当尽可能的小。本文的仿真和实验中，光伏逆变器向电网注入75 Hz的谐波电流[8]，进行电网阻抗比的在线观测。

因为光伏逆变器的控制在d-q同步旋转坐标系上实现，所以注入的75 Hz谐波电流在d轴和q轴电流指令值中所需添加的谐波电流指令为25 Hz，75 Hz谐波注入时所对应的d轴和q轴电流指令如下所示：

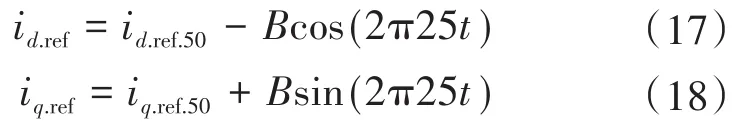
式中：id.ref.50，iq.ref.50分别为直流母线电压控制器的输出和无功功率控制器的输出；B为注入谐波电流的幅值，取决于光伏逆变器的容量。

同时，还需要保证较高的信号噪声比，满足电网对总谐波失真（total harmonic distortion，THD）的要求。实验验证中通过具体的实验，确定了合适的B值。

计算电网阻抗比所需的Vg（h）和IL（h）通过对电网电压和电网电流采样值DFT计算得出。向电网中注入的谐波电流必须满足以下要求：1）不能显著地增加THD，因此注入谐波电流的时间要尽可能短；2）应保证收到足够多的采样点以完成DFT，获得准确的阻抗比结果。通常，注入75 Hz谐波电流40 ms[8]，也就是说，采样点包括了3个周期的谐波电压、电流采样点和2个周期基波电压、电流采样点。这样一来，DFT的基波频率则为fs/N=25 Hz，其中，fs为采样频率，在仿真和实验中，选为3 kHz；N为采样点数，对应采样频率，40 ms共获得电网电压和电网电流各120个采样点，运行逐次累加DFT算法也不会要求很大的存储空间。DFT的基波频率为25 Hz，则在DFT结果中，75 Hz谐波为3次谐波。

DFT计算结果中，3次谐波（75 Hz）表达式为

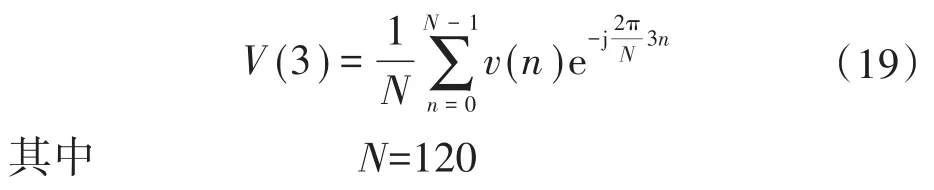
式中：v（n）为采样数据。

通过Matlab/Simulink对以上所描述的电网阻抗在线观测算法进行仿真验证。仿真模型如图2所示，包括了220 V三相电压源、用来模拟电网阻抗的电阻和电感、2 kW负载、1 kW三相光伏逆变器和400 V/1 kW直流电源。

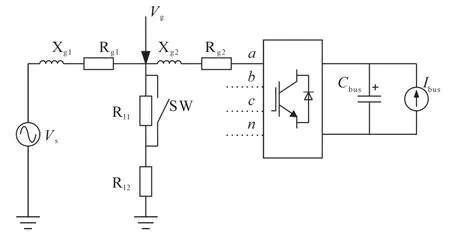
图2 仿真模型示意图Fig.2 Diagram of the simulation model

在线观测所得出的阻抗比与实际的阻抗比的比较结果如图3所示。从图3中可以看出，当阻抗比大于1时，阻抗比的在线观测结果非常准确，相对于实际阻抗比的误差小于5%。而阻抗比小于1时，阻抗比的在线观测结果则不准确，并且相对误差随着阻抗比的减小显著增大。进一步分别分析电阻观测结果和电抗观测结果，如图4所示。其中，横坐标为实际的电网阻抗比，实心点为电网电阻的在线观测结果相对于实际电网电阻的相对误差，空心点为电网电抗的在线观测结果相对于实际电网电抗的相对误差。可以发现电抗观测结果始终非常准确，相对于实际电抗的误差始终小于5%；而电阻的观测结果随着阻抗比的减小显著增大，进而影响了阻抗比观测结果在阻抗比小于1时的准确性。这是由于当电网阻抗中的感性成分增大时，电网电压会发生严重的畸变，从而影响了DFT的计算结果。

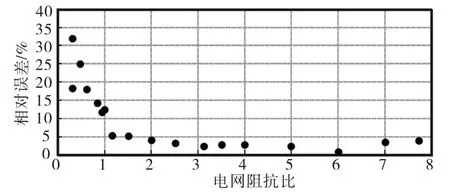
图3 阻抗比观测仿真结果与实际阻抗比的相对误差Fig.3 Relative error between simulated grid impedance ratio estimation and exact value

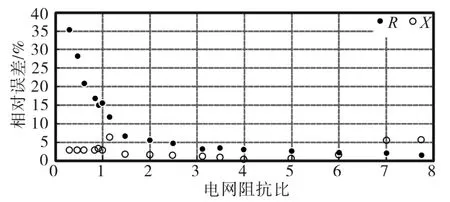
图4 电阻和电抗观测仿真结果与实际值的相对误差Fig.4 Relative error between simulated grid resistance and reactance estimation and exact value

5 光伏逆变器的电网电压控制

基于电网阻抗比在线观测和功率反馈控制的光伏逆变器电网电压控制策略框图如图5所示。其中，电网电压为Vg，电网电流为IL；无功功率控制器根据式（12）搭建，有功功率控制器根据式（13）搭建；电网阻抗比观测器如式（16）所示。电网阻抗比观测触发器用来触发和更新电网阻抗比观测结果——当需要更新电网阻抗比时，它使能75 Hz谐波注入40 ms，相应的DFT计算，进而获得新的阻抗比值，更新光伏逆变器输出的有功电流参考值和无功电流参考值。当电网阻抗比发生显著变化时，如不更新电网阻抗值，则电网电压的控制效果会减弱，从而电网电压幅值会随之波动。实时观测电网电压幅值，能够作为电网阻抗比观测触发器的使能条件。

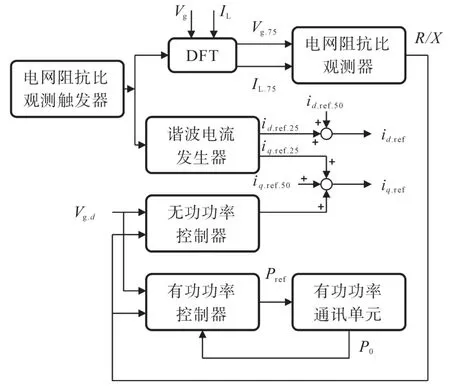
图5 基于电网阻抗比在线观测和有功功率、无功功率控制的电网电压控制策略的控制框图Fig.5 Diagram of the grid voltage control strategy with on-line grid impedance ratio estimation and active/reactive power control

6 实验结果与分析

通过实验对光伏逆变器的基于电网阻抗比在线观测和有功功率、无功功率控制的电网电压控制策略进行了验证和研究，实验平台按照图2搭建。其中，电网阻抗Xg1和Rg1可以调整，以改变电网阻抗比；开关SW用于负载突变时，测试评估控制策略的控制效果。

6.1 电网阻抗比在线观测的实验研究

对电网阻抗比的在线观测进行实验研究。每改变1次电网阻抗比，对电网阻抗比进行400次在线观测。阻抗比观测结果每150 ms更新1次，完成400次电网阻抗比在线观测，需要1 min。实验中一共观测了12组电网阻抗组合。将每组电网阻抗的400次观测结果求平均值，求出其相对于实际的电网阻抗比的相对误差，结果如图6所示。其中，横坐标为实际的电网阻抗比，纵坐标为电网阻抗比的400次在线观测结果的平均值相对于实际电网阻抗比的相对误差。需要特别指出的是，在实验中，注入电网的75 Hz谐波电流的幅值为0.5 A，相对地，注入电网的基波幅值为2.5 A。

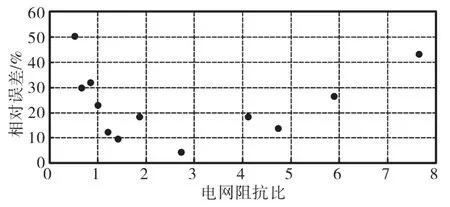
图6 阻抗比观测结果平均值与实际阻抗比的相对误差Fig.6 Relative error between average grid impedance ratio estimation and exact value

当电网阻抗比小于1时，图6的实验结果与仿真结果具有相同的趋势，随着阻抗比的减小，相对误差增加。这是因为电网阻抗中的电抗分量较小，因此，用75 Hz阻抗去近似基波阻抗时误差会增大。然而从图6中可以看出，当阻抗比大于5时，相对误差超过20%，观测结果失去准确度，并且随着阻抗比的进一步增加，相对误差也随之进一步增加。这是因为电网阻抗中的电阻分量增大，降落在电阻上的更大压降影响了在线观测结果。

电网阻抗比大是低压配电网的显著特点，在电网阻抗比较大时，提高电网阻抗比在线观测结果的准确性具有重要的现实意义。为了提高在线观测的准确性，需要增加注入75 Hz谐波电流的幅值。在电网阻抗比为7.64时，向电网注入不同幅值的75 Hz谐波电流，在每个谐波电流幅值下进行400次阻抗比在线观测，对结果求平均值后，相对实际值求出阻抗比在线观测的相对误差。不同谐波电流幅值下的阻抗比相对误差结果如图7所示。

图7 不同幅值谐波电流下，电网阻抗比观测结果的相对误差（电网阻抗比为7.64）Fig.7 Relative error of grid impedance ratio estimation under different harmonic current magnitudes（grid impedance ratio is 7.64）

电网阻抗比在线观测结果中的误差会影响到电网电压控制的性能。与此同时，从相对误差的结果可以观察出，阻抗比观测结果的相对误差始终大于0，这就意味着观测到了比实际电网阻抗中更多的电阻。在电网电压控制中，更多的电网电阻意味着光伏逆变器需要向电网注入比电网电压控制所需更多的有功功率和更少的无功功率。这样，就有可能造成有功电流指令值发生饱和，这种状态是光伏逆变器不希望发生的。对电网阻抗比在线观测器进行修正，可以减小电网阻抗比在线观测结果的相对误差；增大注入75 Hz谐波电流的幅值也可以减小电网阻抗比在线观测结果的相对误差。然而，相对简单直接的有效方法是修改计算有功功率和无功功率指令值式（9）和式（10）中的权重系数，也就是式（7）和式（8），把权重系数与阻抗比的非线性关系改为线性关系，如下：

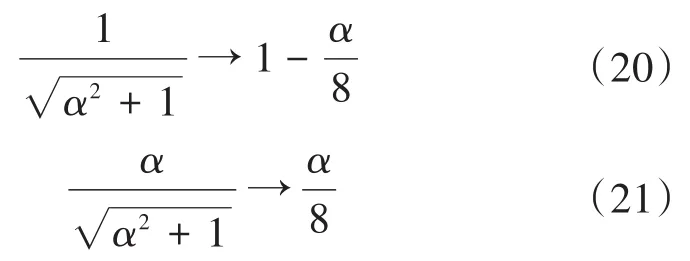
也就是说，阻抗比α对预估的最大阻抗比8进行标幺化，这样就显著减小了权重系数相对于阻抗比的显著变化，减小了阻抗比观测值的相对误差。

6.2 电网电压控制策略的实验研究

在实验平台上，在不同的电网阻抗条件下，对光伏逆变器的电压控制策略进行了实验研究。其中，使用前文所述方法对电网阻抗比进行在线观测。在每个电网阻抗比下，进行两个对比实验，分别是不使用电网电压控制策略的实验和使用电网电压控制策略的实验。

在不使用电网电压控制策略的实验中，能量收集变流器运行在最大功率跟踪点处，光伏逆变器尽全力向电网注入有功功率。在使用电网电压控制策略的实验中，采用本文所研究的控制策略，能量收集变流器工作在电网电压控制所需要的功率点处。

在多个电网阻抗比下，两个对比实验的实验结果如图8所示。其中，横坐标是实际的电网阻抗比，纵坐标是电网电压的标幺值；空心圆点为不使用电网电压控制策略的电网电压标幺值，实心圆点为使用本文所研究的电网电压控制策略的电网电压标幺值。可以看到，电网电压控制显著地降低了过电压发生的程度。不使用电网电压控制策略时，电网电压大部分情况下都超过了额定电压值的110%。而使用了本文所研究的电网电压控制策略，电网电压被有效地限制在额定值的110%以下，满足了光伏逆变器不脱网的普遍标准。此外还可以看到，电网电压控制策略对过电压的控制效果在电网阻抗低的情况下优于电网阻抗高的情况。

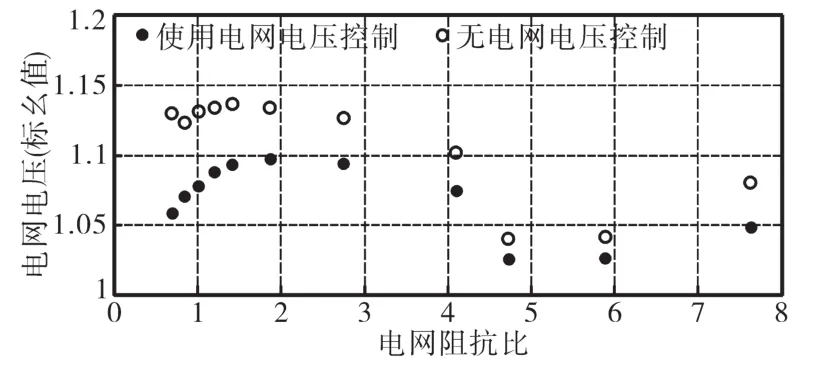
图8 多个阻抗比下，是否使用电网电压控制策略的电网电压对比Fig.8 Grid voltage comparison with and without grid voltage control strategy under various grid impedance ratio

从图8中即可找到这一现象的原因。不使用电网电压控制策略时，光伏逆变器尽全力向电网注入有功功率，当电网阻抗比升高时，可以看到，过电压现象得到了缓解。当电网阻抗比大于4时，电网电压也能够低于额定值的110%。当阻抗比增加时，图2中的Rg2和Xg2两端的电压降增大，因此，电网电压Vg相对于额定值的过电压得到了缓解。与此同时，有功功率控制器要求更小的直流电流，无功功率控制器要求更大的无功电流。而过电压控制主要通过调节有功功率，这就使得在电网阻抗大的情况下，电网电压控制策略的控制效果不如电网阻抗比小的情况下更有效。然而，如果从相对的角度去评价电网电压控制策略对过电压的改善效果，还可以得出以下结果。当电网阻抗比大于1.5时，电网过电压现象改善了大约20%；当电网阻抗比小于1.5时，电网过电压现象改善了大约40%。电网电压控制策略显著改善了电网过电压现象。

7 结论

详细研究了光伏逆变器的电网电压控制策略。通过仿真和实验证明了所研究的策略能够显著地改善电网的过电压现象，同时避免光伏逆变器因为电网过电压而脱离电网。所提出的电网电压控制策略牺牲了部分可收集的光伏能量，达到了维持电网电压，从而保证光伏逆变器持续向电网输送能量的目的。所采用的电网阻抗比在线观测方法能够在电网阻抗比大范围变化的情况下获得准确的电网阻抗比，从而保证电网电压控制策略对过电压的控制性能。仿真和实验充分证明了所研究的电网电压控制策略能够在不同的电网阻抗比下有效地控制电网电压低于额定值的110%，保证光伏逆变器持续并网运行。尽管研究工作得到了有效的效果，具有一定的现实意义，但是，光伏逆变器的容量与电网电压控制效果之间的定量关系以及阻抗观测误差在不同阻抗比范围内所呈现出的趋势也需要通过细化分析，从原理上给出解答，从而进一步减小阻抗观测误差。以上两点是本文工作中存在的不足，也是本文工作的未来研究方向。