基于MPI的高精度归约函数设计与实现*

何 康，黄 春，姜 浩，谷同祥，齐 进，刘 杰,3,4

(1.国防科技大学计算机学院,湖南 长沙 410073;2北京应用物理与计算数学研究所,北京 100000;3.国防科技大学并行与分布处理重点实验室,湖南 长沙 410073;4.国防科技大学复杂系统软件工程湖南省重点实验室,湖南 长沙 410073)

1 引言

近年来，高性能计算HPC(High Performance Computing)在国内外取得了高速发展，在科学研究、工程技术和军事模拟等各个方面有着越来越广泛的应用。

并行计算(Parallel Computing)是以高性能计算机为平台，应用于科学与工程领域，使用多个中央处理单元或多台计算机以协同工作方式解决大规模运算问题的计算模式[1]。并行计算可以加快计算速度，在更短的时间内解决相同的问题或者在相同的时间内解决更多的问题。随着多核处理器和云计算系统的广泛应用，并行已成为有效利用资源的首要手段。目前，国内外在高性能计算系统中最广泛使用的并行编程接口是MPI(Message-Passing Interface)。

MPI是一种基于信息传递的并行编程技术，它定义了一组具有可移植性的编程接口，已成为国际上的一种并行程序标准[1]。MPICH(a high performance portable MPI implementation)是一种最重要的MPI实现。MPICH的开发与MPI规范的制定是同步进行的，每当MPI推出新版本，就会有相应的MPICH的实现版本，所以MPICH最能反映MPI的变化与发展。MPI_REDUCE是MPI中的归约操作函数，该函数对通信子 (Communicator) 内所有进程上的数据进行归约操作，并将计算结果保存至根进程中， 是在并行计算中经常使用的通信函数。

随着信息化社会的飞速发展，人们对于信息处理的要求变得越来越高，计算的大规模、大尺度、长时程和高维数的特点变得越来越明显。浮点计算的舍入误差的累积效应，往往会导致不可信的计算结果，甚至使最终的结果失效。设计高精度的算法，是提高数值计算结果准确性和稳定性的有效途径之一。

基于上述分析，本文基于MPICH提出了一种高精度的归约函数MPI_ACCU_REDUCE，采用无误差变换技术对数值计算的舍入误差进行有效控制。该函数提供了3种高精度的归约运算操作，提供更加丰富的计算的同时，能更进一步提高计算结果的准确性。

2 基本理论

目前，绝大部分的计算机都支持IEEE-754(1985)[2]标准，该标准定义了二进制32位单精度(single)、64位双精度(double)2种类型的浮点算术系统。浮点算术系统的采用使得舍入误差不可避免，在这种超大规模的科学计算中，由于舍入误差具有累积性，每次计算产生的极小误差在累积起来之后，就会使计算结果失去有效性和准确性。所以，控制舍入误差累积，提升数值算法精度成为了研究的重点。

2.1 舍入误差

对于如何有效地控制浮点运算中的舍入误差，最有效的办法就是提高浮点运算的工作精度。1991年，Goldberg[3]阐述了浮点数系统中舍入误差、有效精度等问题对于计算机科研人员的重要性。2008年，IEEE组织考虑到舍入误差累积的影响，对IEEE-754(1985)标准进行扩展，增加了四精度(quadruple，128 bit)浮点算术和十进制浮点算术(decimal arithmetic)等，形成了新的算术标准，简称IEEE-754(2008)[4]，下文简称IEEE-754。根据实现层次的不同，高精度浮点运算的实现可以分为软件和硬件2个层次[5]。软件方法主要是从算法层面实现高精度运算，其灵活性要高于硬件方法。

一个标准的浮点计算模型[6]如式(1)所示：

aopb=fl(a∘b)=

(a∘b)(1+ε1)=(a∘b)/(1+ε2),∀a∈R

(1)

其中op∈ {加，减，乘，除}，∘∈ {+,-,×,÷}，且|ε1|，|ε2|≤u。u为基本算术运算所使用的机器工作精度，又称为单位舍入单元(unit round- off)。在IEEE-754浮点标准的单精度中μ近似等于10-8，双精度中μ近似等于10-16。

该模型给出了浮点数基本运算的误差界如式(2)所示：

|a∘b-fl(a∘b)|≤u|a∘b|,

|a∘b-fl(a∘b)|≤u|fl(a∘b)|

(2)

该过程就是由于计算机字长有限而导致计算产生舍入误差的基本过程。此模型仅在没有下溢情况时才成立。从模型中可以看出，n个浮点数的基本运算的向后误差界限会随着n的增加不断增大。

为了进行误差分析，本文引入2个误差分析符号θn和γn，设n为正整数且nu<1，则有以下结论：

若εi≤u,ρi=±1,对i=1:n,且nu<1，有:

(3)

其中|θn|≤γn=nu/(1-nu)。

2.2 无误差变换技术

无误差变换技术(Error-Free Transformation)是设计补偿模式的高精度数值算法的基本思想。无误差变换的思想是在二十世纪六七十年代由Kahan[7]和Dekker[8]提出的。

无误差变换的思想如下所示：

设a,b是2个浮点数a,b∈F，且fl(a∘b)∈F。可知对于基本的运算，浮点数的误差仍是一个浮点数，所以可以得到：

x=fl(a±b)⟹a±b=x+y,y∈F

(4)

x=fl(a·b)⟹a·b=x+y,y∈F

(5)

使用补偿的方法对计算的结果进行改进，即使用一个巧妙设计的修正项来改善结果，这就是从浮点数(a,b)到浮点数(x,y)的无误差变换。

2.3 基于无误差变换的补偿算法

算法1[8]FastTwoSum

输入：a,b。

输出：x,y。

步骤1x=a+b；

步骤2y=b-(x-a)

FastTwoSum是由Dekker[8]于1971年提出的，算法需要满足|a|≥|b|的条件，共计3个浮点运算量。

算法2[9]TwoSum

输入：a,b。

输出：x,y。

步骤1x=a+b；

步骤2z=x-a；

步骤3y=(a-(x-z))+(b-z)。

TwoSum算法是由Knuth[9]提出的，需要6个浮点运算量。TwoSum不需要先验条件，且在下溢发生时仍然有效。

算法3[8]Split

输入：a。

输出：x,y。

步骤1c=factor×a；%factor=2s+1

步骤2x=c-(c-a)；

步骤3y=a-x。

算法4[8]TwoProd

输入：a,b。

输出：x,y。

步骤1x=a×b；

步骤2[a1,a2]=Split(a)；

步骤3[b1,b2]=Split(b)；

步骤4y=a2×b2-(((x-a1×b1)-a2×b1)-a1×b2)。

TwoProd算法是由Dekker[8]提出的，该算法首先通过Split算法将输入的参数分成2部分再进行计算，需要17个浮点计算量。

当数值计算需要近似2倍工作精度时，double-double 数据格式是最有效、最常用的选择。下面介绍double-double数据格式的数值算法,首先介绍double-double格式数的加法算法add_dd_dd，算法的输入为2个double-double格式的数据a,b,其中ah和bh分别代表a和b的高位，al和bl分别代表a和b的低位，算法输出为一个double-double格式的数据r，rh和rl分别代表r的高位和低位。

算法5[10]add_dd_dd

输入：a=(ah,al),b=(bh,bl)。

输出：r=(rh,rl)。

步骤1[sh,sl]=TwoSum(ah,bh)；

步骤2[th,tl]=TwoSum(al,bl)；

步骤3sl=sl+th；

步骤4[th,sl]=FastTwoSum(sh,sl)；

步骤5tl=tl+sl；

步骤6[rh,rl]=FastTwoSum(th,tl)。

接下来介绍double-double格式数的乘法算法prod_dd_dd。与算法add_dd_dd类似，prod_dd_dd的输入也为2个double-double格式的数据。

算法6[10]prod_dd_dd

输入：a=(ah,al),b=(bh,bl)。

输出：r=(rh,rl)。

步骤1[th,tl]=TwoProd(ah,bh)；

步骤2tl=ah×bl+al×bh+tl；

步骤3[rh,rl]=FastTwoSum(th,tl)。

3 高精度归约函数

求和和求积运算是科学工程计算的基础,随着工程计算的规模越来越大，提高基本运算的准确性对于大规模工程运算具有非常重要的意义。本文以无误差变换技术为基础，提出了高精度的归约函数MPI_ACCU_REDUCE，其包括求和、求积和求L2范数3种高精度归约运算。

3.1 MPI_REDUCE(归约操作)工作原理

MPI_REDUCE是MPI中的归约操作，对通信子(communicator)内所有进程上的数据进行归约操作(比如求和、求极大值和逻辑与等)，这个归约操作即可以是MPI定义的操作,也可以是用户自定义的操作[12]。

MPI_REDUCE函数定义为：

intMPI_REDUCE(void*sendbuf,void*recvbuf,intcount,MPI_Datatypedatatype,MPI_Opop,introot,MPI_Commcomm)

函数接口中的参数定义如表1所示。

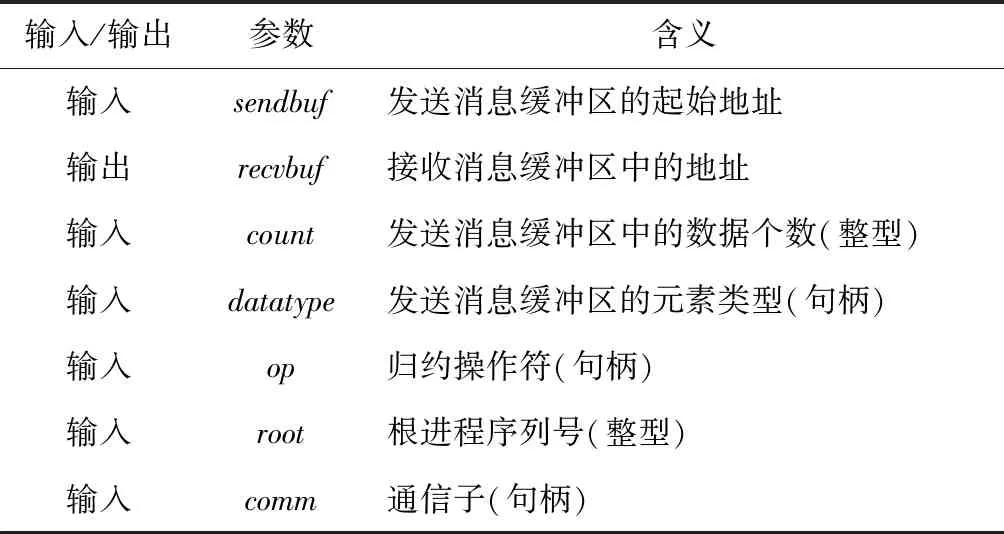
Table 1 Parameter definition of MPI_REDUCE

MPI_REDUCE将组内每个进程输入缓冲区中的数据按op操作组合起来，并将其结果返回到序列号为root的进程的输出缓冲区中。输入缓冲区由参数sendbuf、count和datatype定义，输出缓冲区由参数recvbuf、count和datatype定义。两者的元素数目和类型都相同。所有组成员都用同样的参数count、datatype、op、root和comm来调用此例程,因此所有进程都提供长度相同、元素类型相同的输入和输出缓冲区。每个进程可能提供一个元素或一系列元素，组合操作针对每个元素进行。

3.2 MPI用户自定义操作MPI_Op_create

MPI中已经定义好了一些操作，它们为函数MPI_REDUCE和其他的相关函数提供调用。这些操作对应相应的op。例如：MPI_SUM求和操作，MPI_PROD求积操作等。MPI中也提供了一种用户自定义操作的方式：通过MPI_Op_create()函数将用户自定义的操作和自定义的操作符绑定在一起，实现类似的调用。

MPI_Op_create函数定义如下：

intMPI_Op_create(MPI_User_function *function,intcommute,MPI_Op *op)

其中，function为用户自定义的函数,必须具备4个参数:invec、inoutvec、len和datatype。其中invec和inoutvec分别表示将要被归约的数据所在的缓冲区的首地址,len表示将要归约的元素个数,datatype
表示归约对象的数据类型。

3.3 高精度归约函数MPI_ACCU_REDUCE

虽然MPI中已经定义好了一些简单的操作，然而在大规模计算中，这些操作运算结果的精度无法得到有效的保障。基于此，本文提出了具有高精度的归约函数MPI_ACCU_REDUCE，其包含求和、求积和求L2范数3种高精度的归约运算，提高了归约计算的精度。

MPI_ACCU_REDUCE函数定义为:

doubleMPI_ACCU_REDUCE(void *sendbuf,void *recvbuf,intcount,intoptype,introot,MPI_Commcomm)

函数接口中的参数定义如表2所示。

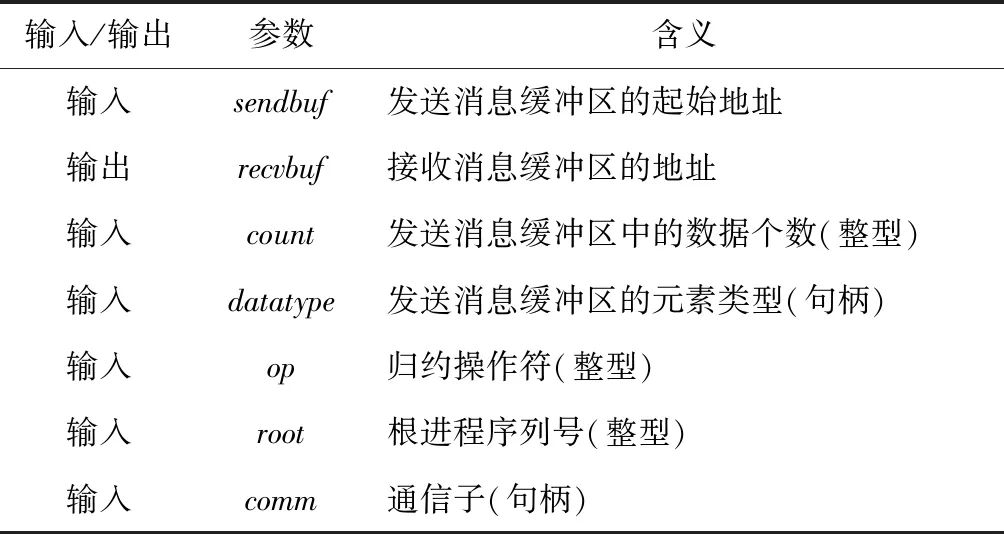
Table 2 Parameter definition of MPI_ACCU_REDUCE

用户在调用MPI_ACCU_REDUCE进行高精度归约时，根据计算需求输入相应的参数，MPI_ACCU_REDUCE函数会根据不同的归约操作符调用不同的高精度运算操作，并将计算结果发送到根进程的接收消息缓冲区中。

3.3.1 高精度求和运算MPI_DDSUM

本文在第2节中介绍了基于无误差变换技术实现的double-double格式数据的加法算法add_dd_dd。MPI_DDSUM操作便是以算法add_dd_dd为基础实现的。

MPI_DDSUM的流程图如图1所示。

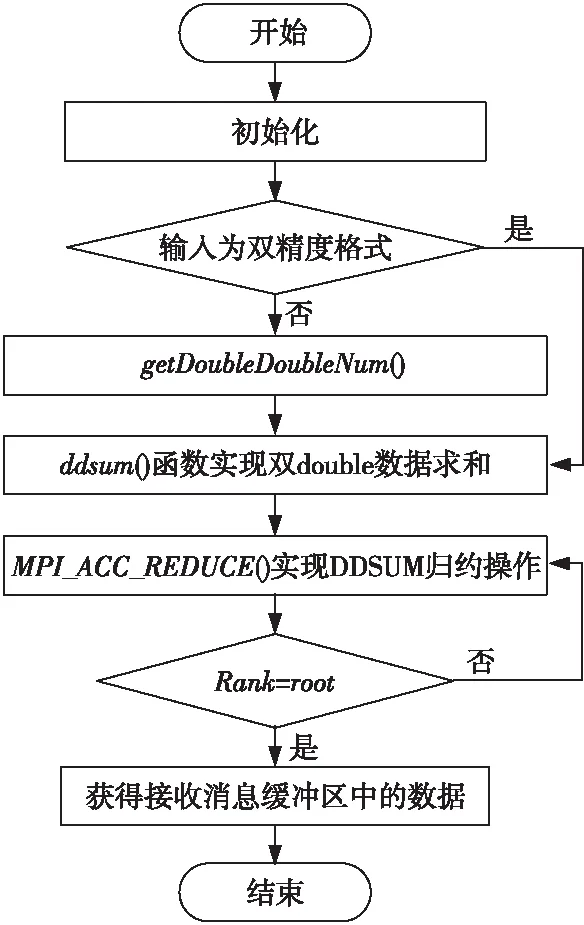
Figure 1 Flow chart of MPI_DDSUM图1 MPI_DDSUM流程图

MPI_DDSUM可以实现对一组double-double数据的高精度求和，通过算法add_dd_dd实现了自定义函数ddsum，使用用户自定义归约操作函数MPI_Op_create将ddsum函数和归约操作符DDSUM联系起来，这样定义的操作DDSUM可以像MPI预定义的归约操作一样应用于各种MPI的归约函数中。

MPI_DDSUM同样可实现一组double数据的求和。用户可以通过MPI_ACCU_REDUCE静态库提供的getDoubleDoubleNum函数将输入的double格式的数据转换成double-double数据。

MPI_DDSUM算法的核心实现如下所示：

…

MPI_Comm_rank(MPI_COMM_WORLD,&rank);

MPI_Comm_size(MPI_COMM_WORLD,&size);

MPI_Type_contiguous(2,MPI_DOUBLE,&ctype);

MPI_Type_commit(&ctype);

MPI_Op_create((MPI_User_function*)ddsum,1,&DDSUM);

MPI_REDUCE(in,inout,count,ctype,DDSUM,root,comm);

MPI_Op_free(&DDSUM);

其中自定义函数ddsum()的核心实现为：

for(i=0;i< *len;i++)

{

temp=add_dd_dd(*inout,*in);

*inout=temp;

in++;

inout++;

}

自定义函数ddsum的主体是算法add_dd_dd。该算法每进行一次加法计算都要进行一次归一化处理，即FastTwoSum操作。归一化处理的目的是保证double-double数的高位和低位严格满足一定的关系，本文对ddsum函数进行改进，提出了统一归一化处理的算法CompDDsum。该算法在最后统一进行归一化处理，然后补偿回原结果。

接下来对统一归一化处理的double-double数据加法算法CompDDsum进行介绍，算法的输入是一组double-double格式的数据xi(i=1,…,n)，xi.hi和xi.lo分别代表数据的高位和低位。

算法7CompDDsum

输入：一组double-double格式的数据xi(i=1,…,n),xi=(xi.hi,xi.lo)。

输出：res。

步骤1 fori=1:n

步骤2xi+1=TwoSum(xi.hi,xx+1.hi)；

步骤3ri+1=ri+xi.lo+xi+1.lo；

步骤4 end

步骤5temp_res=rn+xn.lo；

步骤6[h,l]=FastTwoSum(xn.hi.temp_res)；

步骤7res=h+l。

在自定义函数CompDDsum的基础上实现了更加高效的MPI_CompDDsum操作。比起原始的MPI_DDSUM操作，MPI_CompDDsum在计算的最后统一进行归一化处理，降低了计算成本的同时，几乎没有降低计算精度。

其中自定义函数CompDDsum的核心实现为：

for(i=0;i< *len;i++)

{

temp=two_sum(inout→hi,in→hi);

r[i] +=inout.lo+in.lo;

inout→hi=temp.hi;

in++;

inout++;

}

r[*len-1] +=inout[*len-1].lo;

inout[*len-1].lo=r[*len-1];

3.3.2 高精度求积运算MPI_DDPROD

本小节在双精度乘法算法prod_dd_dd的基础上实现了高精度求积操作MPI_DDPROD，并比较了普通乘法算法与高精度乘法算法prod_dd_dd的误差界。

算法8Prod

输入：一组double格式的数据ai(i=1,…,n)。

输出：res。

步骤1x1=a1；

步骤2 fori=2:n

步骤3xi=xi-1×a1；

步骤4 end

步骤5res=xn。

普通的乘法运算需要n-1个浮点运算量，我们对其误差界进行分析，其中res代表算法的输出结果，a1a2…an为输入数据的精确乘积，eps代表机器精度，该算法误差界为：

|a1a2…an-res|≤γn-1|res|≤

基于算法prod_dd_dd提出了计算一组double-double数据乘积的高精度算法DDProd,算法的输入是一组double-double格式的数据 ，ai(i=1,…,n),ai.hi和ai.lo分别代表数据的高位和低位。

算法9DDProd

输入：一组double-double格式的数据ai(i,…,n),ai=(ai.hi,ai.lo)。

输出：res。

步骤1 fori=2:n

步骤2ai+1=prod_dd_dd(ai,ai+1)；

步骤3 end

步骤4res=an.hi+an.lo。

算法DDprod需要 25n-24 个浮点计算量。

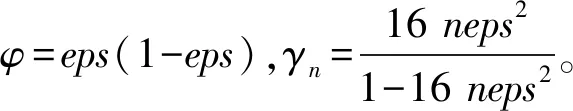
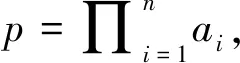
假设在IEEE-754 标准的双精度格式下，此时机器精度eps=2-53，若输入数据长度n满足n<249，则可以获得一个完整准确的舍入结果，即算法DDprod会比算法Prod具有更高的精度。

MPI_DDPROD操作通过算法DDprod实现了用户自定义函数ddprod，通MPI_Op_create函数将ddprod函数和DDPROD操作符联系起来，实现了对数据的高精度求积操作。

高精度的MPI_DDPROD运算具有广泛的应用，可用来计算三角形矩阵的行列式和求浮点数的幂等。

3.3.3 高精度求L2范数操作MPI_NORM

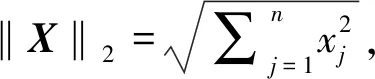
算法10CommonNorm

输入：一组double格式的数据xi(i=1,…,n)。

输出：res。

步骤1 fori=1:n

步骤2acc=acc+xi*xi；

步骤3 end

步骤4res=sqrt(acc)。

接下来介绍带有补偿方案的高精度的求L2范数算法ComNorm()。其中S和P均为double-double格式的数据，sh和ph分别代表s和p的高位，sl和pl分别代表s和p的低位，最终输出的结果res为double格式数据。

算法11ComNorm

输入：一组double格式的数据xi(i=1,…,n)。

输出：res。

步骤1S=[sh,sl]=[0,0]；

步骤2 fori=1:n

步骤3[ph,pl]=TwoProd(xi,xi)；

步骤4[sh,sl]=add_dd_dd(sh,sl,ph,pl);

步骤5 end

步骤6res=sqrt(sh+sl)。

同理，本文通过MPI_Op_create函数实现了用户自定义的归约操作MPI_NORM，实现了高精度的求L2范数函数，丰富了MPI的归约操作。

4 数值实验结果与分析

本文中的所有数值实验都是在 IEEE-754(2008)标准双精度下进行的，计算使用数据均为病态浮点数。其中3种高精度的归约操作均在MPICH下使用C语言实现，数值图表则是使用Matlab生成的。选用多精度浮点运算库MPFR作为比较的基准。

实验均在Ubuntu 16.04系统中进行，gcc版本为4.7，MPICH的版本为使用MPI-3标准的MPICH 3.3.2。

4.1 MPI_DDSUM算法的数值测试实验

在测试MPI_DDSUM时，本文选择多精度浮点运算库MPFR中的加法来作为判断精度是否提升的标准。通过比较MPI_DDSUM和MPI_SUM在不同病态数据量n情况下的相对误差，判断计算结果的准确性。相对误差的计算方式为|res-sum|/|sum|，其中res代表算法的输出结果，sum为精确的加法和，选取MPFR加法的计算结果作为精确的加法和sum。

ReproBLAS的求和用例中提供了一种产生正弦波数据的方式，生成的数据在进行加法运算时具有显著的病态性，本文使用正弦波数据作为测试数据。其数据生成方式为：

sin(2 *M_PI* (rank/((double)size)-0.5))

其中，rank为进程号，size为进程总数，M_PI是C语言中标准库定义的宏。

由图2可以看出，MPI_SUM在病态数据量n=103时，其与MPFR加法求和结果的相对误差已经大于1，即此时MPI_SUM的结果已经失去了准确性。而随着病态数据量n的增大，MPI_DDSUM算法的相对误差稳定在10-15～10-10，较小的相对误差表明MPI_DDSUM的计算结果具有更好的准确性。由此可以得出，相比MPI_SUM求和，MPI_DDSUM求和运算提高了计算结果的准确性。

Figure 2 Relative error comparison between MPI_SUM and MPI_DDSUM under different n图2 不同病态数据量n的情况下MPI_SUM与MPI_DDSUM相对误差对比

4.2 MPI_NORM算法的数值测试实验

本小节选择高精度的求L2范数算法MPI_NORM与常规的求L2范数算法CommonNorm进行比较，使用多精度浮点运算库MPFR实现精确的求L2范数的算法MPFRNorm并作为比较的标准。通过比较在不同病态数据量n下CommonNorm和MPI_NORM的相对误差，判断其结果的准确性。相对误差的计算方式为|res-norm|/|norm|，其中，res代表算法的输出结果，norm为精确的L2范数和，本文选取MPFRNorm算法的计算结果作为精确的范数和norm。

Graillat等[13]提出了一种生成多种类型随机浮点数的方法，其大致思想为针对输入的指数值，分别生成了值域上均匀分布的指数值和有效值，然后根据这个指数值和有效值产生浮点数值。

Graillat等[13]提供的方法可以生成多种不同特点的浮点数据，本文选择范数逐渐向上溢出的向量和一组值极小的向量这2种类型的数据分别进行测试。

先使用一组值极小的向量进行测试，所得结果如图3所示。

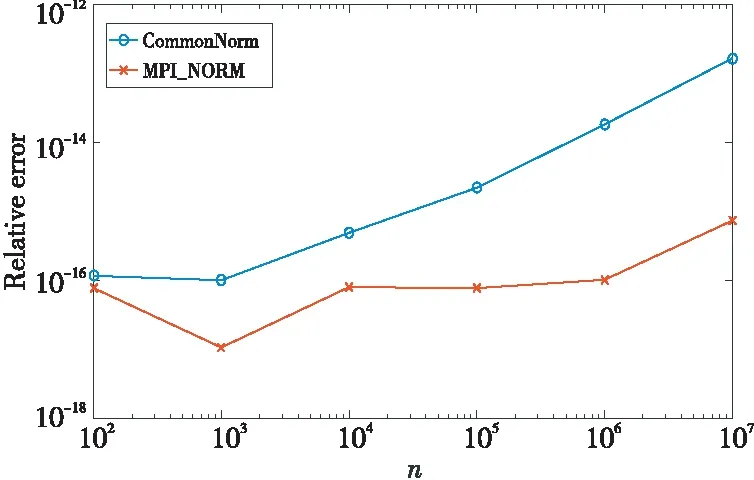
Figure 3 Relative error comparison when testing with extremely small vectors图3 使用值极小的向量进行测试时的相对误差比较

再使用范数逐渐向上溢出的向量进行测试，此时若求得的相对误差大于1，则使其等于1，所得结果如图4所示。

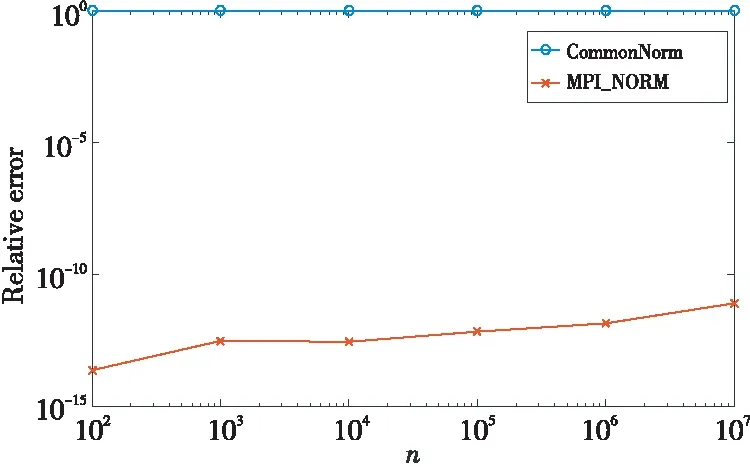
Figure 4 Relative error comparison when testing with vector for which the norm gradually underflows图4 使用范数逐渐上溢的向量进行测试时的相对误差比较

由图3可知，当使用值极小的一组向量进行测试时，此时MPI_NORM算法的相对误差小于CommonNorm的相对误差，且两者的相对误差都小于10-12，表明此时2种算法的结果均具有准确性。随着病态数据量n的增大，MPI_NORM和CommonNorm的相对误差都在增大，由图3可知，CommonNorm算法相对误差上升的速度大于MPI_NORM算法的。

如图4所示，当使用范数值逐渐上溢的向量进行测试时，由于此时必定发生上溢，数据极度病态，CommonNorm算法的相对误差始终大于或等于1，表明此时该算法的结果已经失效。而随着n的增大,MPI_NORM算法的相对误差缓慢上升，处于10-15～10-10，表明此时MPI_NORM计算的结果仍保持准确性。由此可以得出，相比于常规的CommonNorm算法，MPI_NORM算法提高了计算精度。

4.3 性能比较分析

本小节将对高精度归约函数MPI_ACCU_REDUCE的性能进行测试。在不同进程规模的情况下，分别测试MPI_ACCU_REDUCE中的加法操作MPI_DDSUM和乘法操作MPI_DDPROD的运行时间，并与MPI_REDUCE的加法和乘法操作的运行时间进行比较。以MPI_REDUCE中的MPI_SUM和MPI_PROD操作的计算时间作为基准，分别求得加法和乘法计算时间开销的比值，结果如图5所示。

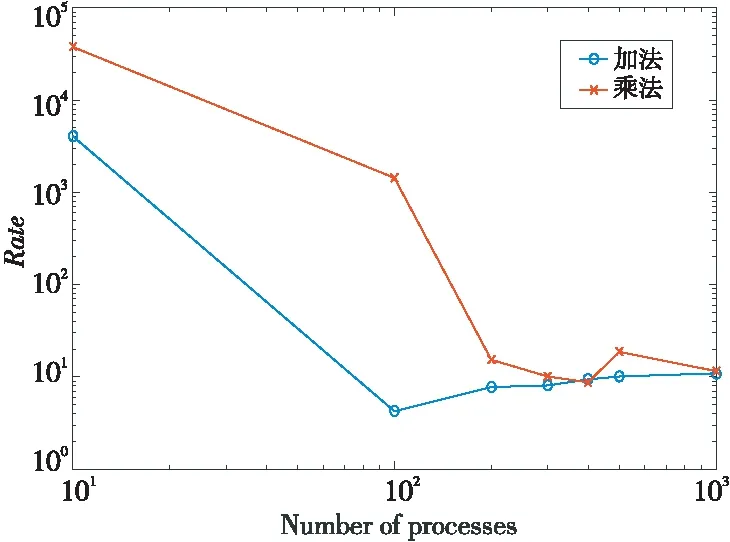
Figure 5 Calculation time ratio of the summation and quadrature algorithms under different process numbers图5 不同进程数下的求和和求积算法的计算时间比

由图5可知，当进程数比较小时，MPI_ACCU_REDUCE中加法操作MPI_DDSUM的计算时间是MPI_REDUCE中的加法操作MPI_SUM计算时间的103～104倍左右，乘法操作MPI_DDPROD的计算时间是MPI_PROD的104～105倍；然而随着进程数的增加，加法和乘法时间开销的比率均逐渐下降，最终稳定在10左右。第3节中对不同算法所需的浮点计算量进行了分析，比起普通的求积和求和操作，高精度的DDSUM和DDPROD操作需要更多的浮点计算量，高精度的求和和求积操作所需的浮点计算量比普通的求和求积操作多10倍左右。算法带来高精度的同时也降低了计算性能，所以本文算法目前更加适用于一些对精度要求更高的场合，同时精度和速度的差异也是在将来的工作中需要改进的地方。

MPI_ACCU_REDUCE性能较低是由于该函数中的高精度运算操作需要更多的浮点运算量，同时还需要调用MPI_Op_create函数新建操作符和数据类型，所以相对于MPI_REDUCE，MPI_ACCU_REDUCE会花费更多的时间。

本文第3节对MPI_DDSUM的核心实现进行了改进，提出了统一归一化处理的CompDDsum。以MPI_SUM计算时间为基准，对核心实现为CompDDsum的MPI_CompDDsum和核心实现为ddsum的MPI_DDSUM进行性能比较测试，分别计算两者在相同进程数下计算时间与MPI_SUM计算时间的比率，结果如图6所示。

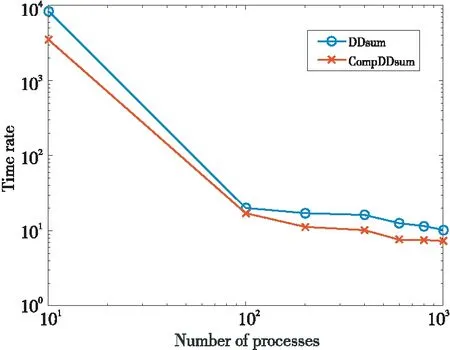
Figure 6 Comparison of calculation time between MPI_DDSUM and MPI_CompDDsum under different process numbers图6 不同进程数下MPI_DDSUM与MPI_CompDDsum计算时间对比

由图6可知，当进程数比较小时，MPI_DDSUM和MPI_CompDDsum的计算时间均是MPI_SUM计算时间的103～104倍左右；随着进程数的增加，MPI_DDSUM与MPI_SUM计算时间的比率逐渐稳定在10倍左右，而MPI_CompDDsum与MPI_SUM计算时间的比率逐渐稳定在7倍左右。所以，只需要改变归一化处理方式，在最后统一进行归一化处理，便可以在几乎不降低精度的情况下，使计算速度有明显的提高，这同时也表明本文算法还有一定的改进空间。

精度提升的同时，带来了性能的下降，所以本文高精度归约操作更适用于一些对计算速度要求较低，而对计算精度有更高要求的场景。这同样表明，在接下来的工作中，应该想办法对高精度的算法进行优化，使其在提高计算精度的同时，性能方面也得到很好的保障。

5 结束语

随着科学计算的大规模、高维数、大尺度和长时程的特性变得越来越明显，高精度的计算方式在未来的并行计算领域变得越来越重要。本文基于无误差变换技术的补偿算法，改进了MPICH的归约函数MPI_REDUCE，实现了高精度的归约函数MPI_ACCU_REDUCE，提出了3种高精度的归约计算操作，包括求和、求积和计算L2范数。数值实验结果表明，高精度归约函数MPI_ACCU_REDUCE有效提高了归约计算的精度，保证了计算结果的准确性。

高精度算法虽然带来了计算精度的提升，然而需要更多的浮点计算量，这使得算法需要更多的计算成本。这就给我们带来了一个新的挑战——如何在计算精度和计算速度之间达到均衡，在不增加计算成本的情况下实现更加优秀的计算精度，这也是未来工作的主要内容。