基于红外热成像的育成期蛋鸡体温检测方法

2021-05-10陆辉山赵守耀王福杰

中国农业大学学报 2021年5期

李沛陆辉山赵守耀王福杰

(中北大学机械工程学院，太原 030051)

蛋鸡养殖业在我国畜牧业发展中占有重要地位。随着现代养殖技术的不断发展，养殖业越来越趋向于规模化、机械化和智能化[1]。快速、精准的感知和分析蛋鸡的健康状况，提高蛋鸡的生产性能，达到健康福利的养殖目的已成为养殖企业以及整个养殖行业的迫切需要[2]。

近年来，关于蛋鸡温度检测的相关研究已经取得了很大的进展。接触式测温采用佩戴传感器的方式，将温度传感器穿戴在鸡体的某些特定部位，实时采集鸡体温度[3-5]；为了减小硬件体积，利用热敏电阻体型小的特性进行测温[6]，该测温方法由于硬件需要供电，无法在长时间观测中使用，同时鸡舍环境复杂，设备容易受潮失灵、掉落，而且易让鸡只产生应激反应，不符合福利养殖的需求。非接触式测温采用红外热成像和数字图像处理技术进行测温[7]，利用卷积神经网络提取特征部位温度，再用BP神经网络反演模型预测蛋鸡真实温度[8]，这种方法由于鸡只小羽毛多，特征不明显，需要大量的特征图片喂入神经网络[9]，标记繁琐，且模型复杂。

温度是生命体的一个重要生理特征，蛋鸡属于恒温动物，当发生应激反应或者在生病的情况下，鸡体体温会发生相应的变化，因此，可以根据蛋鸡的温度变化来判断其健康状况[10]。在养殖场中发现传统的测温方式还是依赖人工检测，主要是测量蛋鸡的直肠温度，有经验的工人可以通过触摸蛋鸡翼下和胸部去判断温度，这样的方式不仅费时费力，主观性强，而且容易让蛋鸡产生应激反应，不符合福利养殖的需求[11]。红外热成像技术属于非接触式测温，测温方式温和，不会让蛋鸡产生应激反应，而且具有精度高，范围广，测温迅速的优点[12]，适合大型养殖应用[13]。目前，红外热成像技术在畜牧业上的应用广泛，大多用于畜禽的病理特征检测[14-20]，但此类畜禽多呈现羽毛少、体型大的特点，使得红外特征明显；而对于蛋鸡这种家禽来说，刚好相反，其具有体型小、羽毛覆盖面积大的特征，导致特征部位不明显，红外测温会受到一定的影响，同时还会受到周围环境的影响，育成期蛋鸡尤为明显，测量存在一定的困难。

本研究拟以育成期蛋鸡为研究对象，分析影响蛋鸡温度的各种因素，并探究鸡体体表温度和真实温度的变化规律，建立两者之间的温度预测模型，以期为蛋鸡红外温度反应真实温度提供依据。

1 材料与方法

1.1 试验动物及饲养环境

试验于2020-07-10在山西省大同市灵丘县汇鑫养殖有限公司进行。随机从鸡舍内挑选20只70日龄健康无异常的绿壳蛋鸡作为试验样本。将20只样本从1，2，…，20编号且随机均分为4组，分别放置在4个相同的鸡笼内饲养，且料槽中饮水和喂食都不受限制；4组样本均处于环境温度为17～30 ℃，相对湿度20%～90%的露天环境中。

1.2 试验仪器

SAT-G95型红外热像仪及指定分析软件SatlrReport，测温范围为-20～600 ℃，精度为±2 ℃，分辨率为384像素×288像素。HRQ-A1型兽用体温计，测温范围为35～43 ℃，示值误差为±0.2 ℃。G2080B型温湿度计，温度测量范围为-20～40 ℃，测量精度±1 ℃；湿度测量范围为10%～90%，测量精度±5%。

1.3 数据采集

试验时间为8:00—18:00，每隔1 h测量1次鸡体体表温度和翼下温度，连续采集10 d，共有2 200组数据。每次测温时都将红外热像仪固定在鸡笼前1 m处，并且将辐射率设定为0.95，同时调好环境温度和湿度参数，待蛋鸡没有出现应激反应时，拍摄5张鸡体侧面红外图像，便于读取蛋鸡特征区域的体表温度；为了减少误差，使用兽用体温计测量鸡体翼下温度时，每次测量5次取平均值；将温湿度计放置在鸡笼和红外热像仪之间，记录每一时刻对应的环境温度和相对湿度。

1.4 蛋鸡体表特征区域选择与分析

使用红外热像仪拍摄的蛋鸡红外热图像见图1。可以看出，育成期蛋鸡体表区域和周围背景区域显示出2种不同的颜色，蛋鸡体表温度明显高于环境温度(图1(a))。由于试验在露天环境中进行，蛋鸡鸡体与环境直接接触，故本试验将蛋鸡身体分为鸡头区域(J)、羽毛区域(Y)和腿部区域(T)3个特征区域，并取鸡体3个特征区域对应的最高温度作为相应特征区域的体表温度。育成期蛋鸡的羽毛没有发育完全，不能阻止热辐射，而且会有部分翼下和胸部区域直接裸露出来(图1(b))，会对真实温度的判断产生一定的影响；同时，Y区域体表温度会随着环境温度的变化发生大幅度的改变，不能作为预测真实温度的条件。

图1 不同温度下育成期蛋鸡鸡体特征区域热分布状况Fig.1 Heat distribution in characteristic regions of layers at different temperatures

1.5 蛋鸡数据处理方法

试验共采集6类数据，分别为环境温湿度、翼下温度、J、Y和T区域的体表温度。分析各变量之间的相关性及相关系数，探究影响翼下温度的变量，进行多元回归分析，建立蛋鸡翼下温度最优预测模型。然后，随机选取5 d蛋鸡温度数据(1 100组)作为训练组，其余5 d数据(1 100组)作为测试组，对模型进行训练和验证。

2 结果与分析

2.1 翼下温度分析

试验期间20只蛋鸡样本翼下温度和鸡体特征区域温度及环境温湿度的平均值见表1。在8:00—18:00期间，环境温度的最大温差为4.6 ℃，相对湿度的最大差值为14.4%，J、Y和T区域的最大温差分别为1.9、6.8和2.3 ℃，翼下温度的浮动范围为0～0.18 ℃。试验是在真实的散养养殖环境下进行的，而且试验期间处于雨季，天气反复变化会对蛋鸡温度有一定的影响。

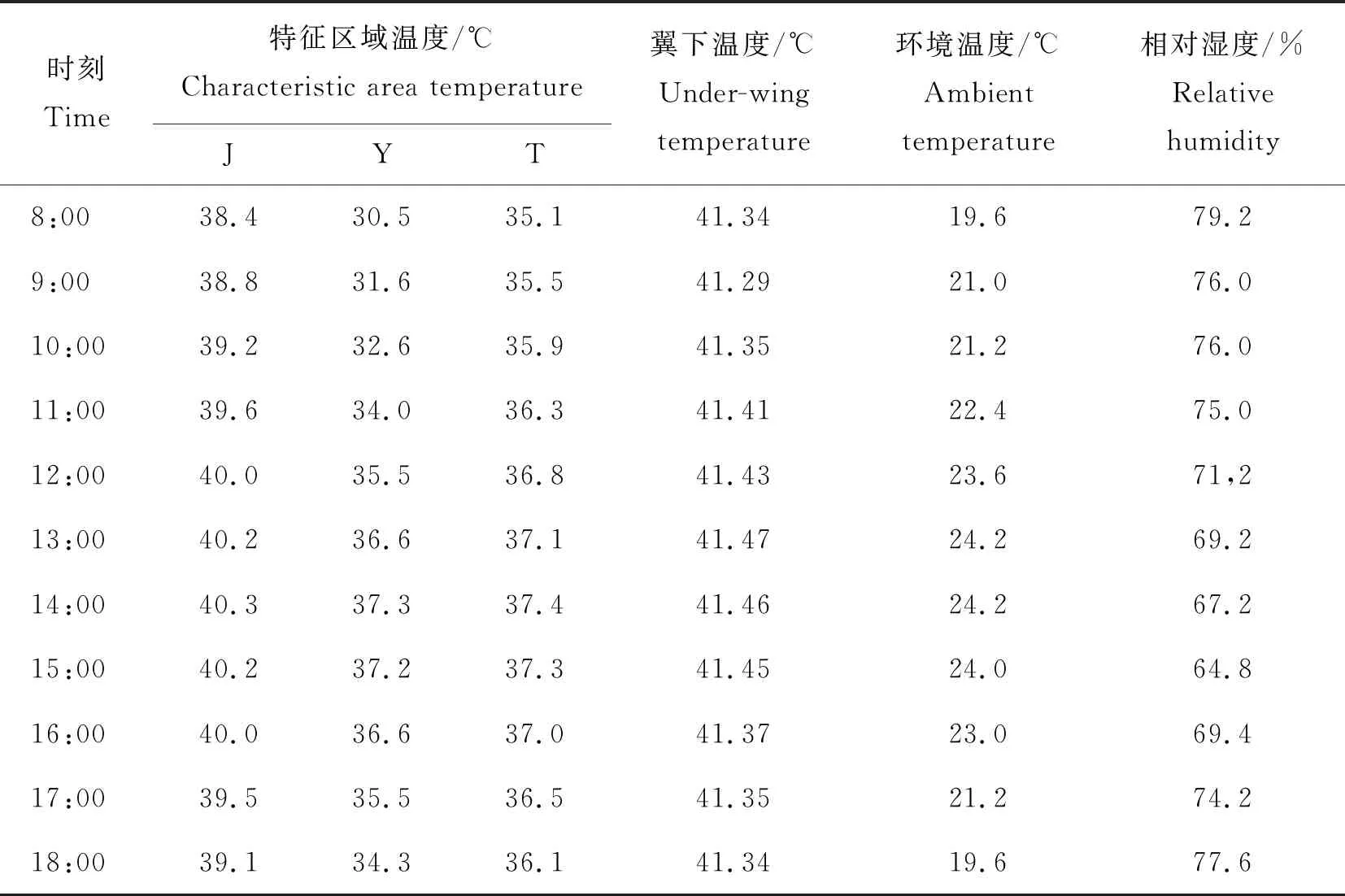
表1 不同时刻鸡体翼下温度和特征区域温度及环境温湿度的平均值Table 1 Average values of temperature under wing, temperature in characteristic area and ambient temperature and humidity at different times

2.2 数据统计与分析

试验数据整理后共有1 650组有效蛋鸡温度数据。鸡体翼下温度、特征区域体表温度和环境温湿度的变化曲线见图2:鸡体3个特征区域的温度都随环境温度的变化有明显的浮动，而蛋鸡翼下温度随着环境温湿度的升高或降低变化较为平稳，影响可以忽略。已有研究表明，在温度>35 ℃、湿度>85%的环境中，相对湿度对蛋鸡温度有显著影响[21]，因此在整个试验的过程中可以忽略相对湿度对蛋鸡温度的影响。

2.3 环境温度与各区域温度的相关性分析

环境温度和特征区域体表温度、翼下温度的相关性分析见表2。在显著性为0.05的校验水平下，环境温度与J区域温度的P值均>0.05；与Y区域温度的P值均<0.05；与T区域温度有80%的P值>0.05；与翼下温度的P值均>0.05。在显著性为0.01的校验水平下，环境温度与J区域温度的P值均>0.01；与Y区域温度有80%的P值<0.01；与T区域温度的P值均>0.01；与翼下温度的P值均>0.01。综上所述，环境温度与Y区域温度显著相关，与其他区域不相关，表明环境温度对Y区域温度影响较大，存在共线性问题，故选择J、T区域温度和环境温度作为预测模型的自变量，从而也验证了本文1.4的分析。

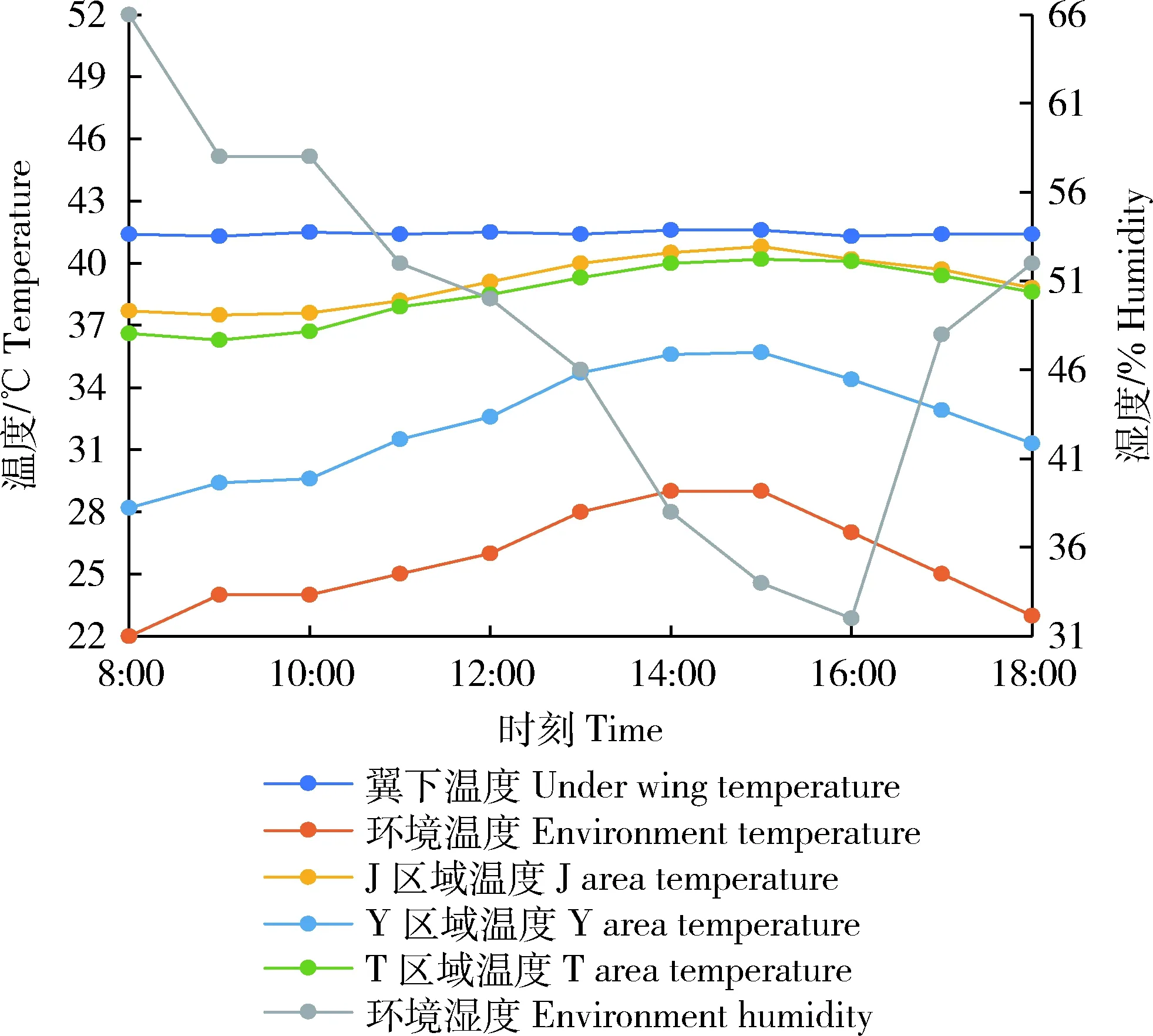
图2 鸡体特征区域和翼下温度随环境温湿度的变化Fig.2 Variation trend of chicken body characteristic areaand under-wing temperature with environmentaltemperature and humidity

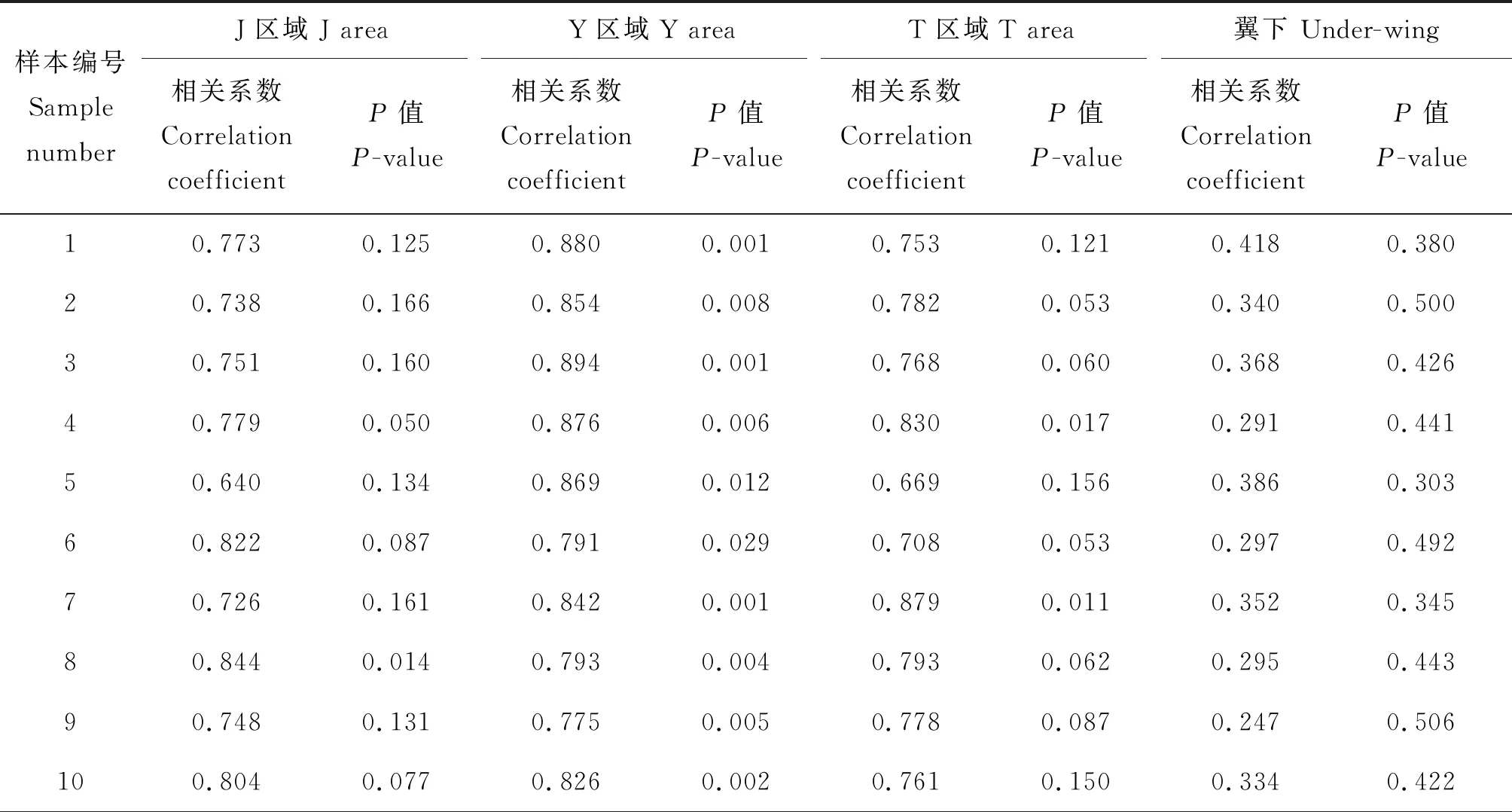
表2 环境温度与J、Y、T区域及翼下温度的相关性分析Table 2 Correlation analysis of ambient temperature and J, Y, T and the temperature of the under-wing area

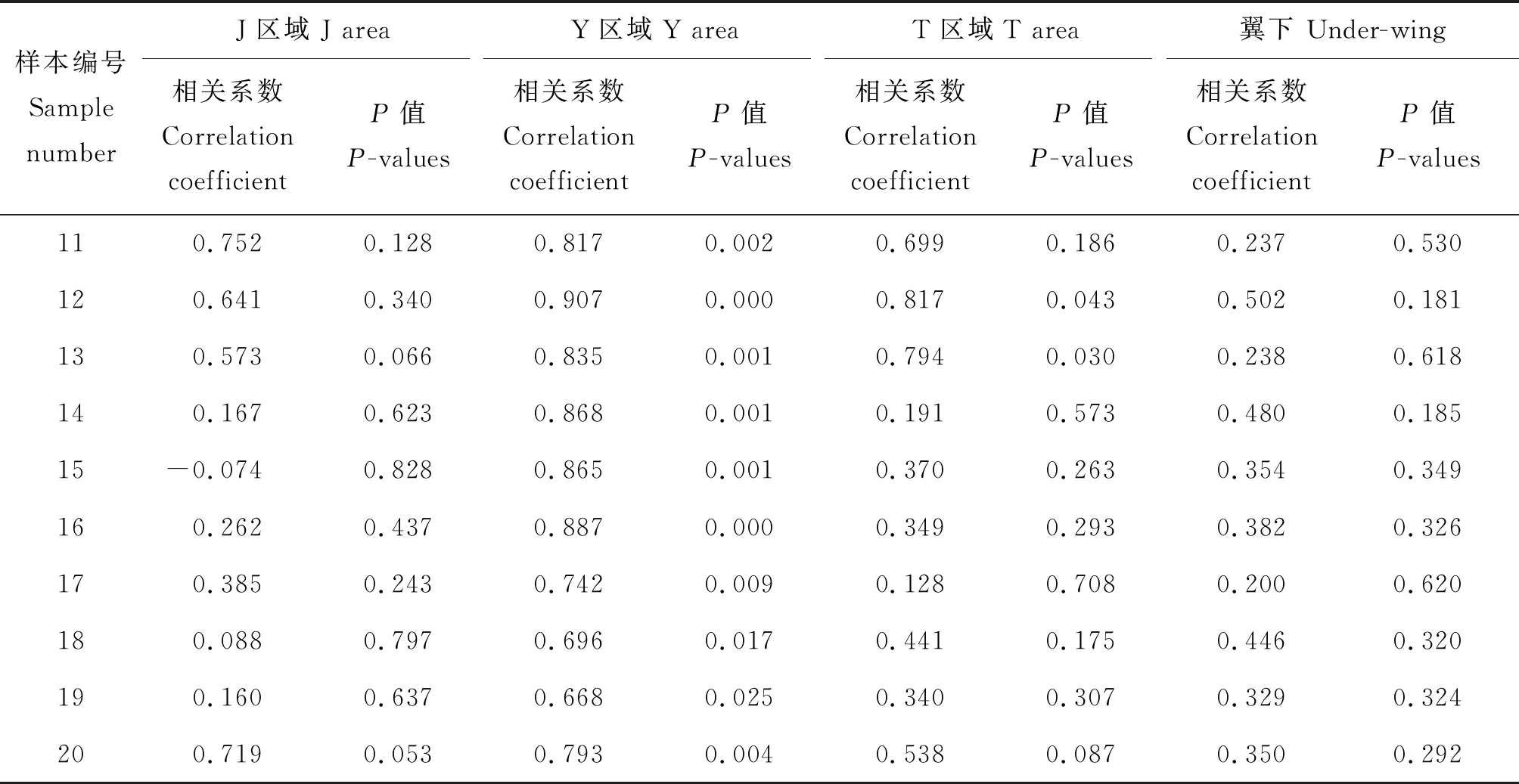
表2(续)

2.4 多元线性回归温度预测模型

在多元线性回归分析中，可以通过模型的可决系数R2与P值判断模型的拟合程度和相关性，R2越大，说明模型的拟合效果越好，预测值的结果越接近真实值。为消除自变量之间的多重共线性，引入了逐步回归法分析，得到3种线性回归模型，结果见表3。这3种模型的P值都为0，达到了显著相关的水平(P<0.01)，说明3种模型中的自变量与翼下温度相关，而且模型3的R2最大，说明模型3相较于模型1、2拟合度最好，效果最优。进一步分析模型3得到该模型方程的系数见表4，其中常量、环境温度、T和J区域温度都符合统计学自变量对因变量显著性的要求(P<0.01或P<0.05)；且3个自变量的方差膨胀系数(VIF)均满足要求(VIF<5)，表明自变量之间不存在多重共线性。综上，模型3满足多元线性回归分析的要求。

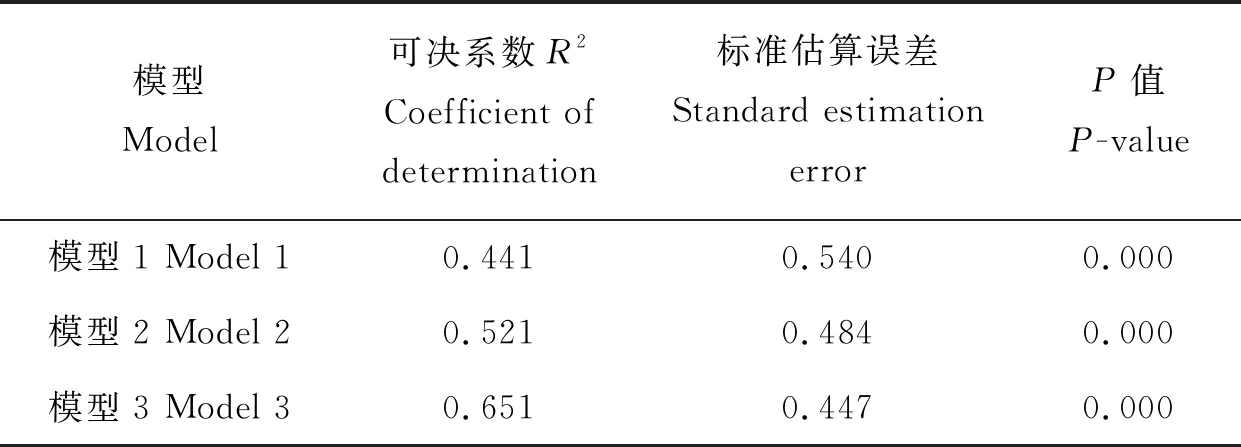
表3 模型信息汇总Table 3 Summary of model information

根据表4回归系数得到模型3的多元线性回归模型方程为：

(1)

为了比较预测温度和实测温度之间的差异，从测试组里随机选出50组数据对模型进行验证，结果见图3，预测值与实测值的最大温差为0.40 ℃，相对误差的平均值为0.38%。

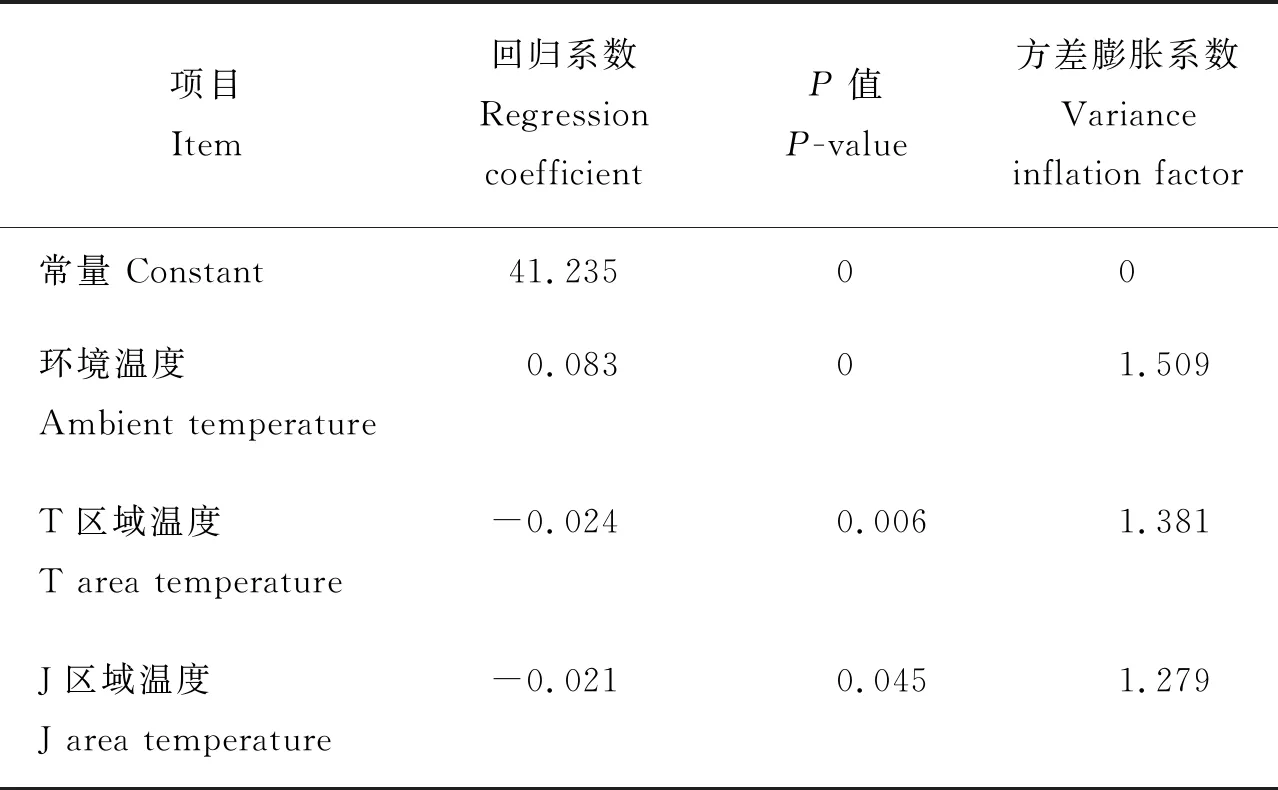
表4 模型3回归系数及显著性和方差膨胀系数分析Table 4 Regression coefficient, significance and variance expansion coefficient analysis of model 3

2.5 多元非线性回归温度预测模型

在线性回归分析中，模型的R2较低，这是由于个别数据强行进行线性拟合导致的。进一步分析试验数据，将环境温度、J和T区域温度(自变量)与翼下温度(因变量)分别进行曲线拟合，发现自变量与因变量在二次方时，R2最大，拟合效果最优。按照图4流程建立多元非线性回归预测模型。

由以上分析将非线性模型函数预设为：

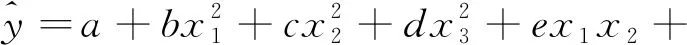
(2)

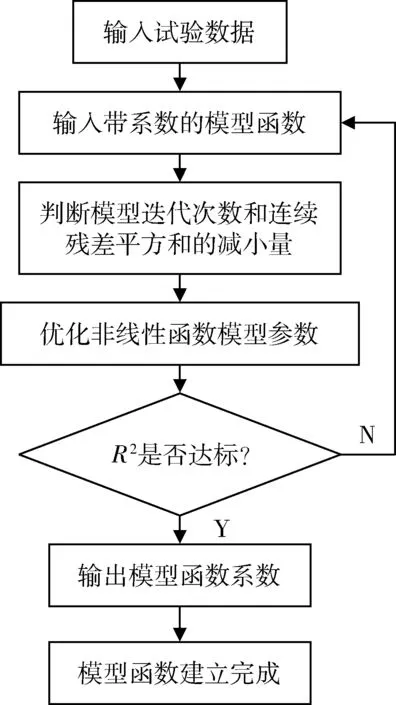
图4 建模流程图Fig.4 Modeling flow chart

模型函数在迭代计算结束之后停止，其连续残差平方和的减小量达到了要求，R2=0.851，修正后模型方程系数估计值见表5，得出模型方程为：

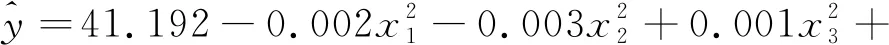
(3)

在测试组里选取50组数据对模型函数进行误差验证结果见图5，预测值和实测值的最大温度差为0.18 ℃，相对误差平均值为0.17%。

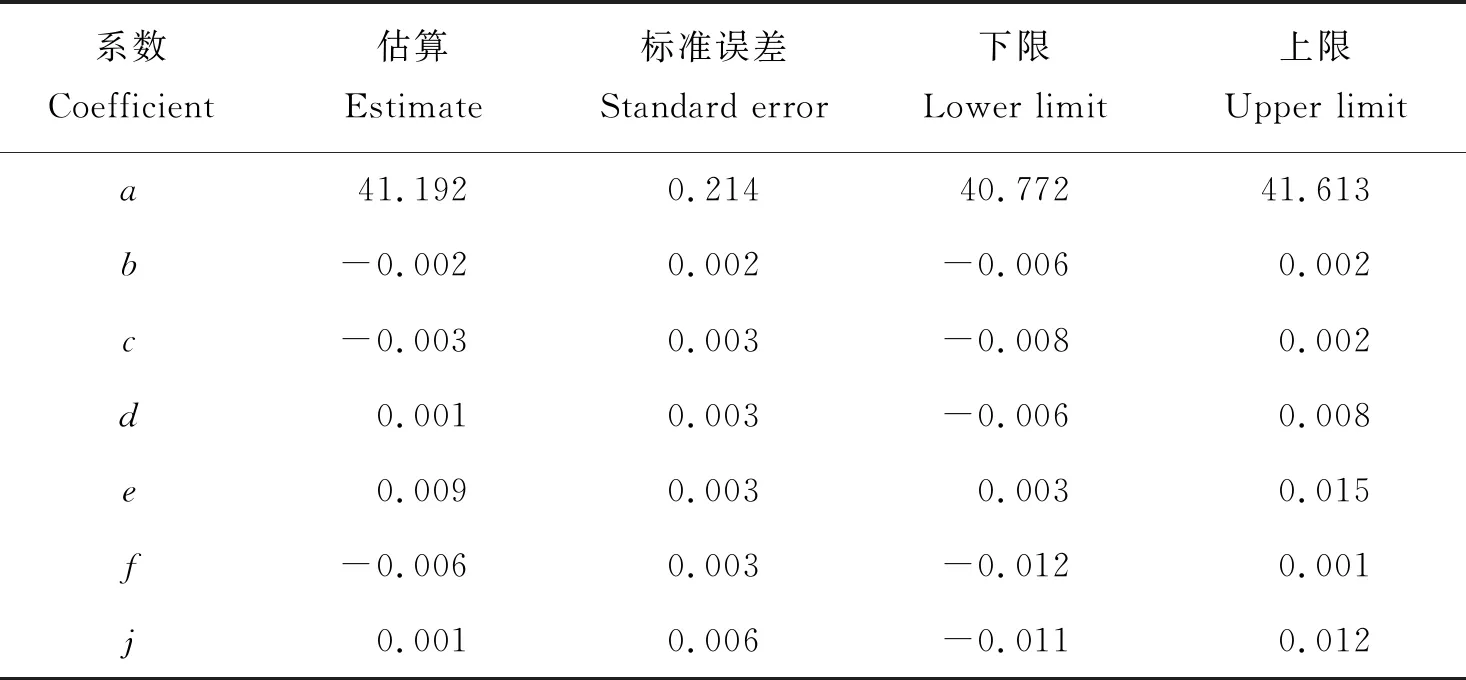
表5 非线性模型方程系数估算值Table 5 Estimated coefficients of nonlinear model equation

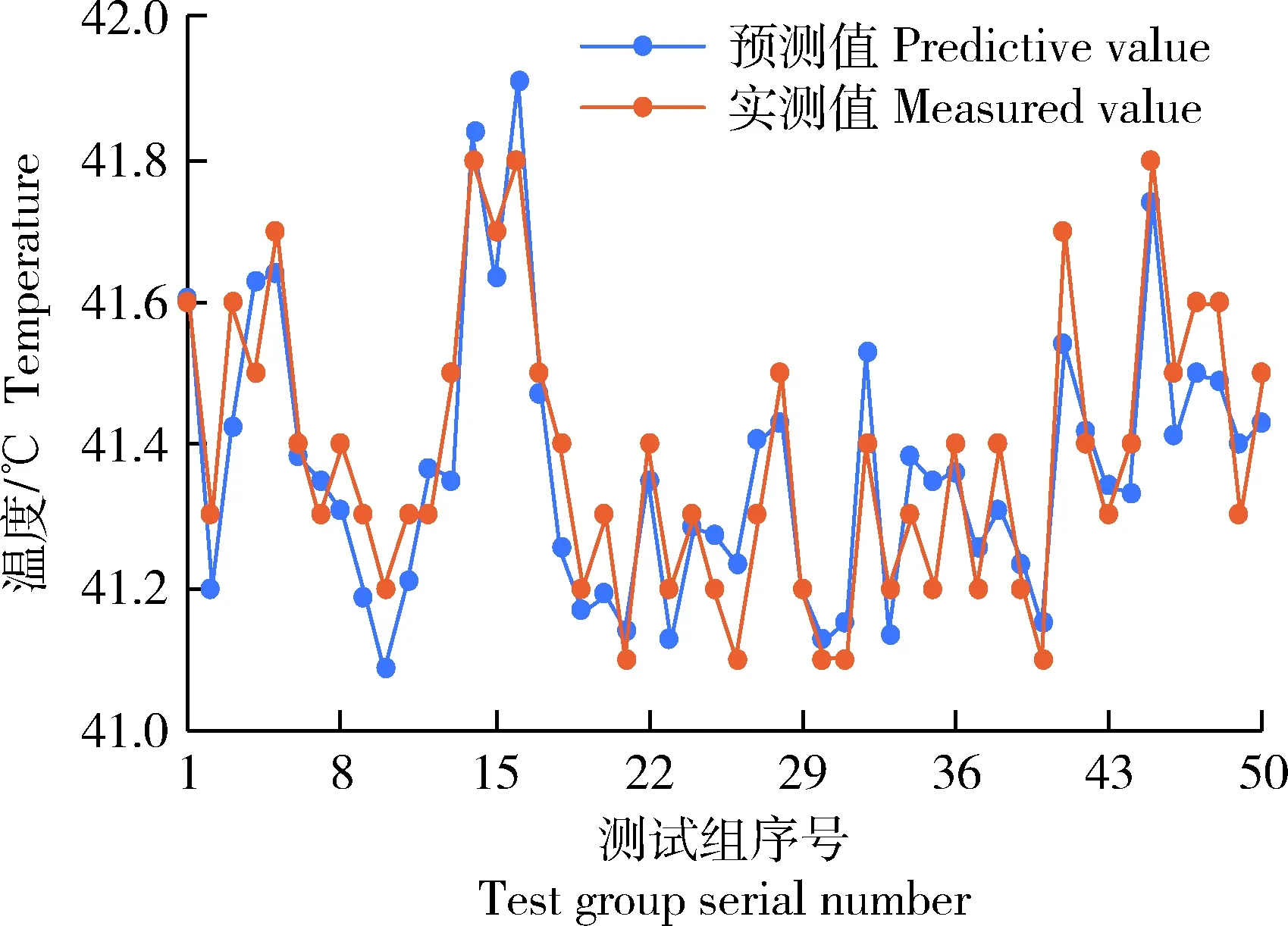
图5 非线性模型测试组温度预测值与实测值对比Fig.5 Comparison of predicted and measuredvalues of nonlinear model test group

2.6 线性与非线性模型对比分析

由式(1)和(3)可知，线性回归模型方程的R2=0.651，非线性回归模型方程的R2=0.851，表明多元非线性回归模型拟合效果更优；由图5可知，预测值和实测值的重合点多，且上下浮动范围小，表明非线性模型优于线性模型；从测试组验证结果看，在线性和非线性预测模型下，预测值与实测值的最大温差、平均相对误差分别为0.40 ℃、0.38%和0.18 ℃、0.17%，非线性模型的误差为线性模型的一半。