分散供应链中混合生产的产品质量战略

姜沂秀，宋炳良

(1.上海海事大学 经济管理学院，上海 201306；2.南通大学 经济与管理学院，江苏 南通 226001)

在20世纪90年代早期，Peter Drucker和Tom Peters等商业专家建议公司经营核心业务而将非核心业务外包[1]。此后，许多商界领袖接受了这一建议，业务外包快速增长。如今，业务外包已成为供应链的一个普遍特征，并为全球经济增长做出了重要贡献。但是，有些人认为过于依赖外包供应商可能会导致市场整体表现下滑。原因包括缺乏长期的研发(R&D)竞争力，不兼容的战略目标，较长的交付周期，较低的质量控制，较高的交易成本，较差的交付可靠性和生产能力的丧失等等[2-3]。

混合生产(即企业将产品生产部分外包部分自制)，作为一种可以有效缓解业务外包风险的战略，可以帮助管理者提高生产力、控制关键业务，并且能够在出现任何问题时提供快速更换外包供应商的机会。

早期的外包决策是基于成本的，现在的外包决策则更多基于产品质量[4]。这可能是因为外包对外包供应商质量控制能力较低[5]。因此，外包采购方应定义一些激励机制，以提高外包供应商的产品质量。

有关供应链管理领域的质量战略，已经有了广泛的研究。Xu[6]调查制造商−零售商渠道的联合定价和产品质量决策。Kaya[7]将供应商做出努力决策的外包模式和制造商做出努力决策的自制模式进行比较。Xie等[8]研究不同供应链渠道的质量决策模型。Xiao等[9]研究两家竞争供应商−制造商的外包决策。Zhu[10]运用Stackelberg博弈在需求不确定的情况下确定最佳外包价格、零售价格和外包质量。

现有文献大多侧重于横向企业的质量竞争，很少关注上下游的2个企业之间的质量竞争(而这种竞争在商业实践中常见)。本文拟采用Tullock竞赛函数，对处于上下游的制造商和供应商，进行产品质量竞争方面的分析。

1 建模

本文主要关注混合生产。而与混合生产相对应的产品质量战略还包括单一外包(即企业将产品生产全部外包)和单一自制(即企业将产品生产全部自制)，三者在模型中可以通过参数的不同设置来取得，后面两者将在第3节进行研究，以便与混合生产进行比较分析。模型符号定义如表1所示。

表1 主要变量及参数说明Table 1 Description of main variables and parameters

其中， Qm和 Qs是决策变量，其他变量是外生的。模型还假设 p＞w≥cm＞cs。 p＞w 和 w＞cs是直观的，因为参与者不会获得负的利润。而 cm＞cs表示供应商比制造商具有成本优势[11]。另外，根据常识，可以预期供应商将收取比制造商的边际生产成本更高的批发价格，即 w≥cm，这也是在低成本外包中建立的[3]。

此外，本文还假设市场需求对参与者及其竞争对手的产品质量很敏感。参照文献[5]和文献[12]，本文使用以下线性模型表示总量需求。

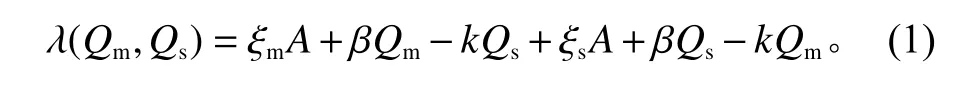
为确保总需求λ 更多地受自己而非竞争对手产品的质量变化影响，假设 β＞k。

考虑制造商选择混合生产，所有产品将由制造商和供应商共同制造。为了将每个参与者的产品质量水平与需求份额联系起来，本文采用标准的Tullock竞赛函数来模拟制造商和供应商之间的质量竞争。而且，制造商和供应商保证向消费者提供符合潜在市场需求的特定质量水平的产品，即在给定 Qm和 Qs的情况下，式(1)可以变化为

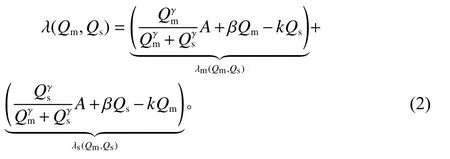
其中，参数 γ (0 ＜γ≤1)表示能够对潜在需求份额有所影响的质量努力程度。参数 γ越大，质量竞赛就越激烈。

通过式(2)，每个参与者的利润函数可以描述为

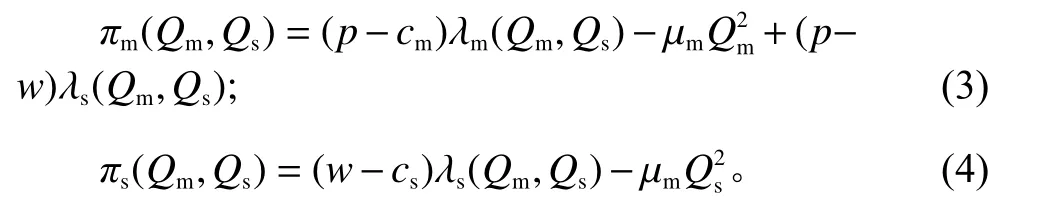
命题1假设 0＜γ≤1，质量竞赛博弈具有纯战略纳什均衡的唯一解，见式(5)和式(6)。

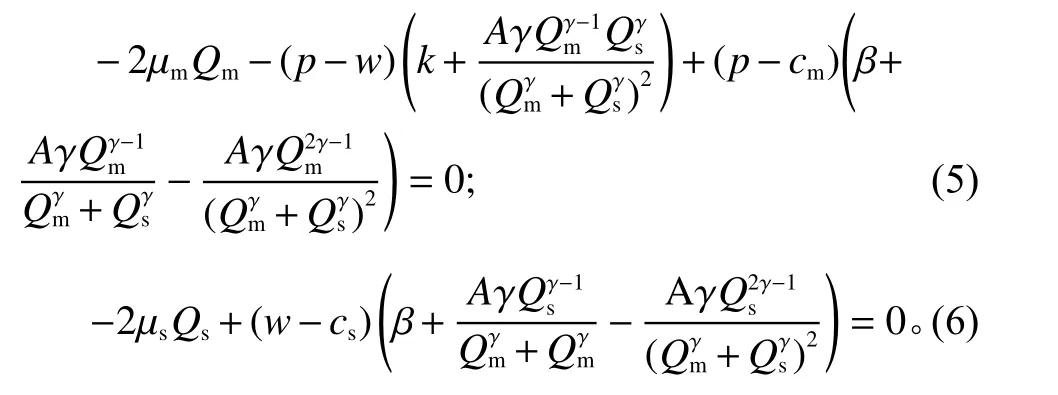
证明将式(2)代入式(3)和式(4)，得

式(7)和式(8)分别对 Qm和 Qs求两阶导数，得

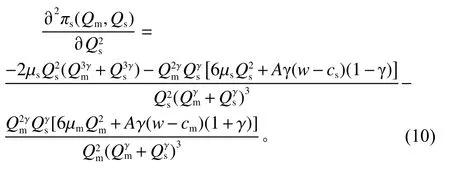
对于纯战略纳什均衡的唯一性，使用单一映射定理来证明。从式(7)和式(8)，可以得出二阶雅可比矩阵J的行列式为

由条件w ≥cm＞cs和0 ＜γ≤1，已知

当制造商选择混合生产时，命题1表明存在与质量决策相对应的纯战略纳什均衡唯一解。但由于式(3)和式(4)的支付函数过于复杂，闭环的纳什解无法推导得出。

2 比较静态分析

在混合生产的质量竞赛模型中，参数γ 显示了对潜在需求份额有所影响的质量努力程度(等价于市场需求系数)。但γ 对于纳什均衡唯一解是否重要？

推论1假设z表示供应商质量努力 Qs与制造商质量努力 Qm的 相对比例系数，即时，纳什均衡唯一解 ()会 随着参数 γ的增加而增加；当时，纳什均衡唯一解 ()会随着参数 γ的增加而减少；当时，纳什均衡唯一解()不会随γ的变化而变化。

推论1说明歧视性参数 γ对均衡的影响取决于供应链成员质量努力的相对比例系数。由于 0＜γ≤1，则只有z ＞e或 z →0时 ，不满足条件而这种情况在质量竞赛模型中很难得到满足有两方面原因。1) 二次成本函数表明这种支出的收益递减[3,12]。在这个成本函数下，如果供应商设定相对较高的质量水平，则可能无法获得正的利润水平；同时当产品质量已经相当高时，质量改进会非常困难和昂贵[13]。2) 由于公司的质量表现会受制于技术和研发能力[14]，供应商和制造商的产品质量差距不可能特别大。

推论2产品质量和的均衡解随着市场需求潜力A的增加而增加。

推论2反映市场需求潜力A对于纳什均衡的影响，指出了2个参与者对产品质量的努力程度会随着A的增加而增加。

推论31)随着p的增加而增加；当供应商强势时，会随着p的增加而增加；当供应商弱势时，会随着p的增加而减少。2) 当制造商强势时，会随着w的增加而增加；当供应商强势时，会随着w的增加而增加。

推论3将价格参数(销售和批发价格)的比较结果与质量竞赛中的参赛者地位相关联。

当销售价格上涨时，制造商希望获得更多的需求份额，以获得更多的利润，从而努力提高产品质量。而供应商对销售价格上涨的反应取决于其在质量竞赛中的地位。如果供应商是强势的，其将提高质量以阻止制造商赢得比赛；而如果供应商是弱势的，由于无法获得最大的需求，其将降低质量努力以降低质量成本。

当批发价格上涨时，只有强势者才能提高质量，而弱势者对于批发价格上涨的反应不确定。从计算结果来看，结果可能取决于如何确定批发价格。例如，当 w=cm时，可以证明，在质量竞赛中无论是强是弱，制造商都会随着批发价格的上涨而提高努力水平。

假设cm＞cs，cs=c 和且t＞1)，用参数t来分析边际生产对于纳什均衡成本差异的影响。

推论41)随着t的增加而减少。2) 当供应商强势时，随着t的增加而减少；而当供应商弱势时，随着t的增加而增加。

推论4表明，制造商的质量努力在成本差异中不断下降。供应商如果在竞赛中强势，其质量努力将随参数t的增加而减少；如果供应商在竞赛中弱势，其能够通过提高质量努力获得更多的需求份额，从而有赢得比赛的激励。

比较静态结果如表2所示。其中，*表示ln zγ＜N/A表示不可获得；“+”表示纳什均衡解与参数正相关；“−”表示纳什均衡解与参数负相关。

表2 比较静态结果Table 2 Comparative static results

表2中的结果由隐函数定理推导得来。从表2可以看出，比较静态结果可能取决于每个参与者在质量竞赛中的状态。

3 生产战略的比较结果

适当的竞赛函数是否真正使混合生产战略超越传统生产战略？本文从产品质量、内生需求和参与者利润等角度，对混合生产以及单一外包和单一自制进行比较。通过设置歧视性参数，寻求更有效的竞赛函数来实施混合生产。

当Qs= 0时，模型转换为单一自制；当Qm= 0时，模型转变为单一外包。两者的比较结果如下。

命题2假设符合条件则1) 由于γ ∈(0,1]， 存在市场需求潜力A的阈值当0＜A≤时，； 当 A＞时，存在唯一的，使 0＜γ＜时； 当 γ=时，；当＜γ＜1时 ，； 2) 当 γ =0时 ，；而当0＜γ≤1时 ，

与单一外包相比，混合生产能鼓励供应商提高产品质量。然而，这种战略是否有利于制造商的质量提升，取决于市场需求潜力A和歧视性参数γ。如果A足够大，与单一自制相比，激烈的竞争可以提高制造商的产品质量。图1为混合生产中γ对产品质量的影响。参数的默认值为µm=µs=1， cm=1， cs=0.5，w=2 ，p=6 ，β=1，k =0.6。

人们会期望制造商始终受益于供应商的质量提升。因此与单一自制相比，制造商可能会降低质量的努力，即部分产品生产外包只是影响供应商质量输出的一种威胁。但是，本文证明了制造商可以通过质量竞赛提高质量，特别是在歧视性参数 γ比较大时。这可能是因为制造商和供应商之间存在的内部和外部质量竞争。例如，在图1(c)中，在竞争对手赢得质量竞赛后，制造商会迅速提高产品质量，使其比单一自制时更高。

命题3假设当 w=p时，纳什均衡唯一解()满 足和。当且仅当γ=0时 ，等式成立。

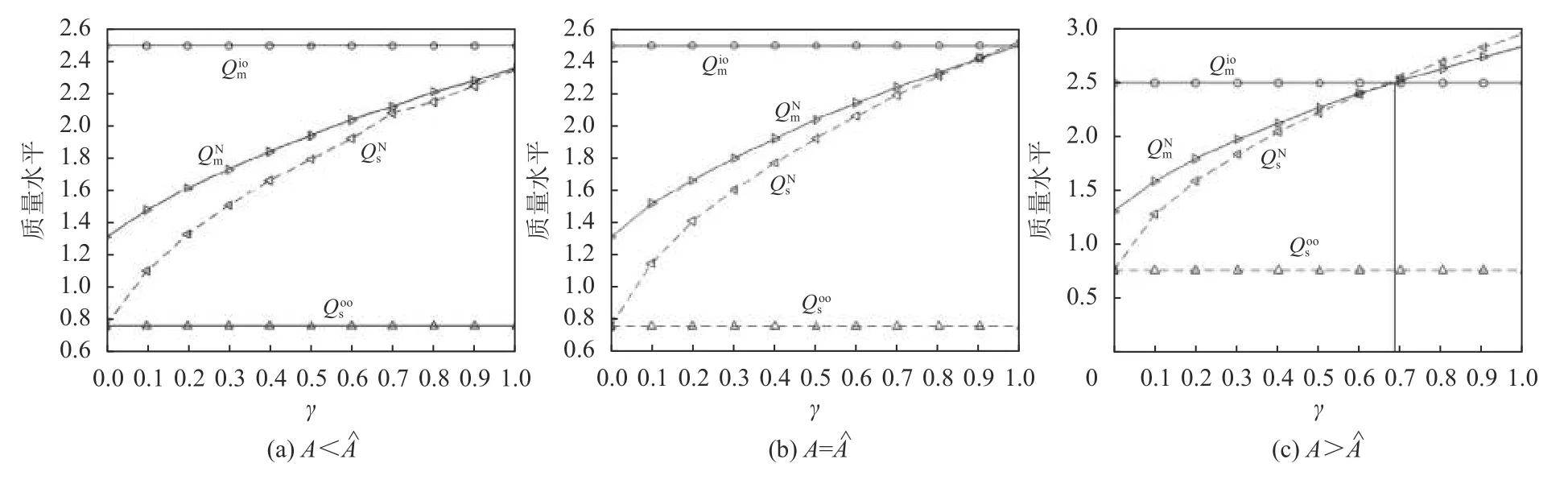
图1 参数 γ和纳什均衡唯一解Figure 1 The unique Nash equilibrium versus parameter γ

当批发价格足够大时 (w =p)，基于式(3)，制造商无法从销售供应商的产品中，获得更多利润。这意味着2个参与者在质量竞赛中，有类似的支付函数。在这种情况下，质量竞赛不再是引导供应商质量提升的威胁，却会鼓励每一位参赛者提高产品质量。因此，本文预计实施质量竞赛无法获取供应商在混合生产中的所有利润，而且，怀疑更激烈的竞争是否能够获取整个制造商的利润，因为供应商可以更低廉的生产成本制造产品。

命题4假设 A ≥且 γ ≥，如果

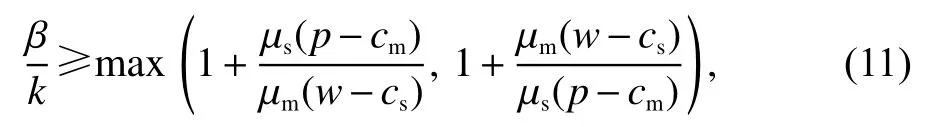
总需求 λN要比单一自制下的需求 λio以及单一外包下的需求 λoo要大。

命题4强调了相对质量响应的重要性。通常，如果相对质量响应性满足式(11)，则模型中的质量竞赛无疑会增加供应链的总需求。此外，由于纳什均衡随着市场需求潜力A和歧视性参数γ 增加，当满足式(11)时， λN−λio和 λN−λoo的 差异会随着A和 γ的增加而增加，如图2和图3所示。参数的默认值为µm=µs=1， cm=1， cs=0.5， w=2 ，p=6 ，β=1，k=0.2。

图2 λ N −λio 和参数A与γFigure 2 λ N −λio versus A andγ

图3 λ N −λoo 和参数A与γFigure 3 λ N −λoo versus A andγ

供应链上相互竞争的上下游成员是否有动力参与混合生产？因为利润函数太复杂，无法与其他生产战略(单一自制和单一外包)相比，本文无法确定此问题的分析结果。但是基于大量的数值例子，观察1和2提供了这个问题的答案。此外，表3提供了解释混合生产对每个参与者利润的影响。

观察1假设符合式(11)，如果批发价格足够低，与单一自制和单一外包相比，混合生产会增加制造商的利润。而且，质量竞赛越激烈，制造商获得的利润就越多。

观察2与单一外包相比，无论批发价格是多少，供应商都会受到实施混合生产的伤害。而且，质量竞争越激烈，供应商所承受的损失越大。

观察1结果表明，当批发价格足够低时，制造商可能更倾向于混合生产。另外，当质量竞赛很激烈，制造商可以通过实施混合生产获得更多的利润。但是，如果批发价格变高，，当时，两者之间的制造商利润差异增加，如表3所示。表3中参数的默认值为A =30， µm=µs=1， cm=1， cs=0.5， p=6 ，β =1，k =2。从表3可发现，如果批发价格不断上涨，随着γ 的增加，先增加，后减少。

观察2中，实施混合生产对供应商可能是有害的。这可能是因为供应商无法获得整个市场需求潜力，同时需要设定更高的产品质量。

表3 批发价格w和参数 γ对于利润的影响Table 3 Impacts of wholesale price w and parameter γ on profits

当批发价格足够低时，制造商可能偏好烈性较强的质量竞赛；而当这个价格变大时，制造商可能偏好烈性较弱的质量竞赛。但是，供应商偏好不与其客户进行质量竞争。这说明正确设定质量竞赛函数对于参与者加入混合生产的激励非常重要。

4 结论

为了有效提高外包产品(服务)质量，本文提出了一个新的生产战略，即二级分散供应链的混合生产，由一个供应商和一个制造商组成。探讨的主要问题是混合生产在产品质量方面，是否优于单一外包或单一自制？

为了反映供应链上下游成员之间在混合生产中的质量竞争，本文首先采用Tullock竞赛函数建立一个非合作的博弈模型解释市场需求潜力如何分配。通过使用单一映射函数，证明在歧视性参数比较温和的条件下，该质量竞赛博弈的纯战略纳什均衡是唯一的。本文进一步调查模型参数对纳什均衡的影响。基于这些比较静态结果，证明实施混合生产，与单一外包相比，肯定会带来供应商的质量改进；同时在一定条件下，制造商的产品质量高于单一自制的质量。此外，本文发现如果相对质量响应性足够大，在质量内生需求函数的情况下，混合生产可能会增加整体需求。最后，本文证明，当供应商收取的批发价格足够低时，制造商偏好混合生产。供应商由于无法获得整体需求，因此会受到混合生产的伤害。此外，本文还发现在歧视性参数较大情况下的竞赛理论中，制造商偏好烈性较强的竞赛；而供应商偏好烈性较弱的比赛，以减轻竞争利润损失。

本研究为分散供应链的混合生产的实施提供重要的见解。这项工作还有几个扩展需要考虑，以用于未来的研究。本文讨论垂直纳什渠道结构的情况，即供应链上下游成员同时设定产品质量，但是“制造商Stackelberg”和“供应商Stackelberg”需要进一步研究。此外，还需要考虑在多个制造商之间的水平和垂直质量竞争的模型。最后，本文只关注一个决策变量(质量)，这个战略可以扩展到集成其他变量(如未来的价格和交货时间)的模型。