基于全相位FFT的油套环空中声速计算方法

仵 杰，王 轲，刘彦萍，高建申

(1. 西安石油大学电子工程学院，陕西西安710065；2. 陕西省油气井测控技术重点实验室，陕西西安710065)

0 引 言

动液面是抽油井在正常生产时，油管和套管环形空间的一个液面。在油气井开采过程中，地层的供液能力制约着产量和综合效率的最大化。动液面不仅是反映地层供液能力的一个重要指标[1]，而且是油田确定合理沉没度的重要依据。在动液面测量中，有两个关键问题：一是声速的准确确定，二是正确识别液面回波位置(通过到达时刻计算)。关于声速的准确确定，目前主要有基于短时平均幅度差函数(Average Magnitude Difference Function, AMDF)计算抽油井套管环隙内声速的方法[2]；人工神经网络方法[3]；基于短时自相关函数(Autocorrelation Function, ACF)的套管环隙内声速计算方法[4-5]。关于液面回波位置的识别，目前主要有低通椭圆滤波器滤波方法[6]，分型模糊控制滤波方法[7]，基于谱减算法的方法[8]。以上方法虽然取得了一定的成果，能较好地对声速进行计算以及对动液面信号进行滤波并辨识其位置。但上述方法都存在一些不可避免的缺点，例如基于AMDF算法计算出的声速并不是很平滑的变化，选取不同的帧对结果影响很大；谱减算法中的过减系数和谱减系数的取值会影响测量结果，如选取不当最终可能导致计算回波位置时产生更大的误差，准确性反而下降。为了更准确地计算出动液面深度，首先需要准确地估算油套环空中的声波速度。针对这一问题，本文在详细分析油气井中声速测量原理的基础上，提出采用一种性能更优的谱分析方法——全相位快速傅里叶变换(all-phase Fast Fourier Transform, apFFT)对接箍信号进行谱分析，然后根据谱峰位置进一步计算出声速。全相位 FFT方法的提出主要是为了解决信号直接截断后其频谱的幅值、频率、相位产生的误差问题[9-11]，目前主要应用于岩石声发射源定位[12]、合成孔径水声通信运动补偿[13]、非稳态电力信号[14]、航空设备的旋转叶片异步振动辨识[15]、感应式磁力仪的频谱校正[16]、时移相位差估计器[17]、数字滤波器[18]、电力系统相量测量装置[19]等方面。本文对此方法的实验验证中，分别采用快速傅里叶变换(Fast Fourier Transform, FFT)和apFFT对不同信噪比的模拟接箍信号进行频谱分析与比较，根据各自的频谱计算出声速并比较其精度。然后将两种方法应用于实际接箍信号的处理中，进一步验证apFFT在声速计算时的优越性。

1 油气井中声速测量原理

图1为油气井动液面测量的物理模型。动液面测量仪器安装在井口，仪器产生的脉冲声源经套管和油管之间的环空传播到动液面，声波接收传感器以一定采样率采集油套环空中、动液面和油井周围的声波反射信号。油井内数千米长的油管是由许多节长度基本一致的短节油管连接而成，在两节油管的连接处存在向外凸出的接箍，如图1所示。采用具有一定压力的套管气或压缩空气作为发声源来产生次声波，次声波在套管环隙内向下传播的过程中，遇到油管接箍和油气界面后均会产生特定频率的反射波，如果套管环隙内声速为一常数且声波不衰减以及无其他干扰，则从井口接收的接箍波应接近于一个周期信号，但由于套管环隙内各处声速有可能不同且声波会衰减并存在其他干扰，因此，在动液面检测过程中，接箍波一般为准周期信号。深度较浅的油管接箍对声波具有明显的反射，油管接箍是周期性存在的，那么反射波形也可视为周期性出现。利用这一特点，可计算波形走过一个油管所需的时间，进而可计算出声波速度：

图1 油气井液位测量示意图Fig.1 Schematic diagram of liquid level measurement in oil and gas well

2 基于全相位 FFT的动液面声速计算方法原理

动液面声速计算方法以谱峰位置的提取作为核心，谱的辨识度及谱峰位置的测量精度至关重要。全相位FFT法具备相位不变性和克服频谱泄露的特性[20-22]，从很大程度上解决了传统FFT法测相位时因数据截断带来的误差，同时抑制了谐波的干扰。该算法的数据处理精度高、过程简单、运算量较小，便于实时操作。

下面是对全相位FFT算法原理的简单介绍。

假设原始数据长度为2N−1的序列x(n),n = − N + 1 ,− N + 2 ,… , N −1，对其进行全相位数据预处理的第一步为列出包含序列中心点x(0)的所有长度为 N的序列。 xi(n): i, n = 0,1,… ,N −1，共形成 N个包含x(0)的N维向量：

当f( n)和b( n)均为矩形窗时，数据处理成为无窗全相位数据预处理；当其中一个为非矩形窗时，数据处理称为单窗全相位预处理；当两个均为非矩形窗时，数据处理称为双窗全相位数据预处理。

然后，将全相位预处理的结果向量进行传统的FFT运算，得全相位FFT(apFFT)结果：

最后，对经过全相位处理的N点序列进行峰值搜索即可获得相对应的幅值和频率。在动液面声速计算的应用中，需对谱峰位置进行提取，将谱峰的横坐标数值代入式(1)计算出声速。

3 正演模型实验及结果分析

本文采用COMSOL软件，在压力声学模块下，以高斯脉冲作为信号源构建理想情况下的动液面声波反射模型，而在实际生产中，需将声压信号转换为电压信号，所以最后采集到的数据其波形幅值单位为V或mV。设空气中的声速为343 m·s-1，采样频率为Fs=2 000 Hz。计算接收点处总声压场并提取其总声压场数据，因此所得波形幅值单位为Pa。将其作为实验所用的模拟信号，波形如图2所示：

图2 声波法测油井模拟信号波形图及接箍信号波形放大图Fig.2 The waveforms of analog signal by acoustic wave method for measuring oil wells and enlarged coupling wave respectively

对上述所得接箍数据进行传统 FFT与全相位FFT谱分析，求取油套环隙中的声速，并对结果进行分析对比。实验中，对纯净的模拟接箍信号加入不同频率、不同强度的噪声，以测试两种方法的抗噪性及稳定性，并根据各自所得的频谱计算声速，对比其精度。

加入的噪声信号为

式中：中、低频正弦干扰的采样频率为Fs=2 000 Hz，A为随机噪声幅值，2N−1为数据采样点数，n′ =1 ,2,… 2N−1，r a ndn( 2N−1,1)表示产生2N−1行、1列的正态分布随机数。

对采样点数为373的含噪接箍信号分别加入不同强度的噪声，在同等信噪比条件下分别进行传统FFT与全相位FFT谱分析，并根据各自的频谱求取油套环隙中的声速，计算其相对误差。表1为两种方法的声速计算结果。

表1 FFT和apFFT方法对模拟数据声速估算结果的对比Table 1 Comparison of the estimated results of acoustic velocity by FFT and apFFT spectrums

由表1可知：在无噪情况下，FFT法所得声速值与apFFT所得值相同，两者的相对误差都很小。但是在加噪情况下，根据FFT谱 计算出的声速会出现误差很大的现象，而根据apFFT谱计算出的声速仍保持很小的误差值。由此可知apFFT法比FFT法的抗干扰能力更强，稳定性更好，声速计算精度更高。

将表 1中信噪比为无噪、2.307 3 dB信号的FFT与apFFT谱图进行分析对比，结果如图3、图4所示。

图3 FFT和apFFT得到的无噪接箍信号的频谱Fig.3 The spectrums of noise-free coupling signal obtained by FFT and apFFT

图4 含噪接箍信号及其频谱Fig.4 The noise-containing coupling signal and its spectrums obtained by FFT and apFFT

在无噪情况下，虽然根据FFT谱和apFFT谱计算出的声速值相同，但是两者的频谱形状有较大的差异，apFFT谱更为规则，几乎没有谱泄露的现象。对比加噪信号的两种频谱，发现FFT谱已经出现谱峰缺少的现象，这会导致声速计算的误差增大，精度大幅下降。而apFFT谱仍保持正常数目的谱峰，为准确计算声速提供了较好的前提条件。

4 现场接箍反射波频谱分析与声速估算

由于实际中无法获得真正的声速值，因此估算出的声速并没有评价标准。如果实际数据中能够看出接箍波的时域波形特征，则先以此进行时域估算，算出一个声速值作为评价频域方法性能的参考。前文讲过，声速在油套环空中还有变化的可能，那么仅用时域波形估计声速的方法局限性较大。当从深井采集而来的数据中接箍波形特征不明显时，时域估算法的误差将会很大，且声速是否在不同深度有所变化也难以获知。频域法对波形特征的依赖性较小，能够在接箍波时域波形特征不明显时对声速进行有效估算，而在频域法中又将寻求精度更高的方法实现对声速更为准确的估算。

现选取采样频率为 470 Hz的实际测井数据中的接箍信号进行FFT和apFFT频谱分析。浅井信号波形及其分区如图5所示。

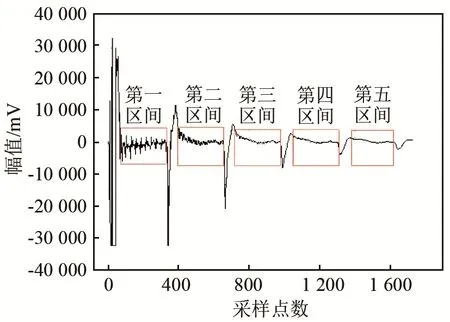
图5 浅井信号波形及其分区Fig.5 The signal waveform of shallow well and its partition

由于浅井信号接箍波段数据距发射源较近的部分时域波形特征较为明显，随着波的传播，其时域波形特征逐渐不明显，为此截取其中波形明显的数据段进行声速估算，估算出的声速值作为后续研究的参考。图5的实测信号波形中，第一区间接箍波波形特征较为明显，可根据其时域波形估算声速。而第二区间至第五区间接箍波衰减较严重且被噪声淹没，因此不易于声速估算，此时需采用频域法进行估算。实际中，如果条件恶劣或环境复杂将会存在从第一区间开始接箍波就不易识别的情况，因此根据时域波形估算声速的方法并不通用。

检测出第一区间接箍波峰所对应的采样序列号为101、128、156、184、213、242，据此求出声波信号渡越每个接箍所对应采样序列号的平均值为

则浅井接箍信号第一区间时域声速的计算过程为

本文提出采用频域分析法来估算声速，分别采用FFT和apFFT算法做谱分析并进一步估算声速。下面是采用这两种频域法对图5各区间中接箍波的声速进行估算的过程，其频谱如图6所示。

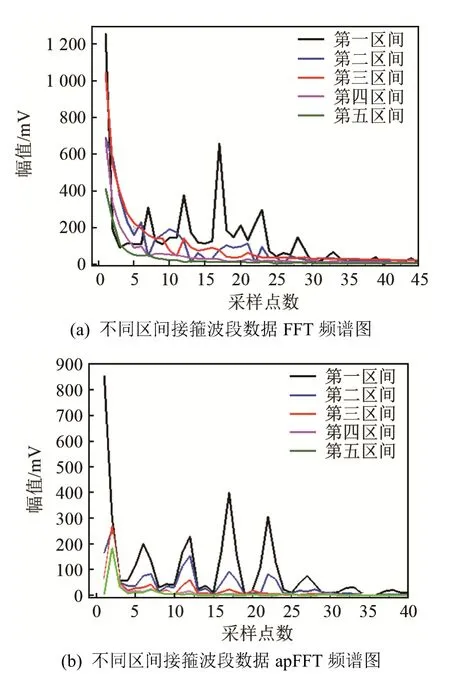
图6 FFT和apFFT得到的不同区间接箍波段数据频谱图Fig.6 The spectrums of coupling wave data in different regions obtained by FFT and apFFT

可以看出，图6(a)中第一区间谱峰规律性较强，第二区间到第五区间谱线杂乱无章，有效峰值少，将会导致声速计算误差大。图6(b)中第一区间到第三区间的谱峰规律性均较强，一致性较好，第四区间到第五区间才显示出峰值很小的谱线。由此说明apFFT算法的性能优于FFT算法。

表2为浅井信号不同区间声速估算结果对比。表2中第二列第一个值是根据接箍信号的时域波形估算的声速，也以此为参考来评价通过两种谱分析方法所估算的声速。由于从第二区间开始，接箍信号的时域波形已不易辨识，因此无法据此估算声速。从表2的第三列和第四列可以看出，根据接箍波第一区间的谱分析，FFT法所得声速值与apFFT所得值相同，第五列和第六列所示两者的相对误差都很小；但是在第二区间和第三区间，根据FFT谱计算出的声速误差很大，而根据apFFT谱计算出的声速仍保持很小的误差值。此外，根据apFFT谱分析法还可得知，该井中的声速基本不变。通过对上述图表的分析，得出一致结论：apFFT法比FFT法的抗干扰能力更强，稳定性更好，适用于有效信号很微弱的情况，通过该法估算出的声速精度更高。

表2 浅井信号不同区间声速估算结果对比Table 2 Comparison of the estimated results of acoustic velocity in different regions by FFT and apFFT spectrums

深井信号及接箍波段数据的频谱如图7所示。

由于深井信号接箍波段的数据信号更弱，其时域波形特征更加不明显，如果根据其时域波形进行声速计算，则会存在较大的问题。图7(a)所示的是来自深井的信号，靠近发射端的接箍波段信号时域波形仍能呈现出一定的规律性。为此，截取其中波形特征明显的数据段进行时域的声速估计，检测出每个波峰所对应的采样序列号为 77、107、136、166、197。

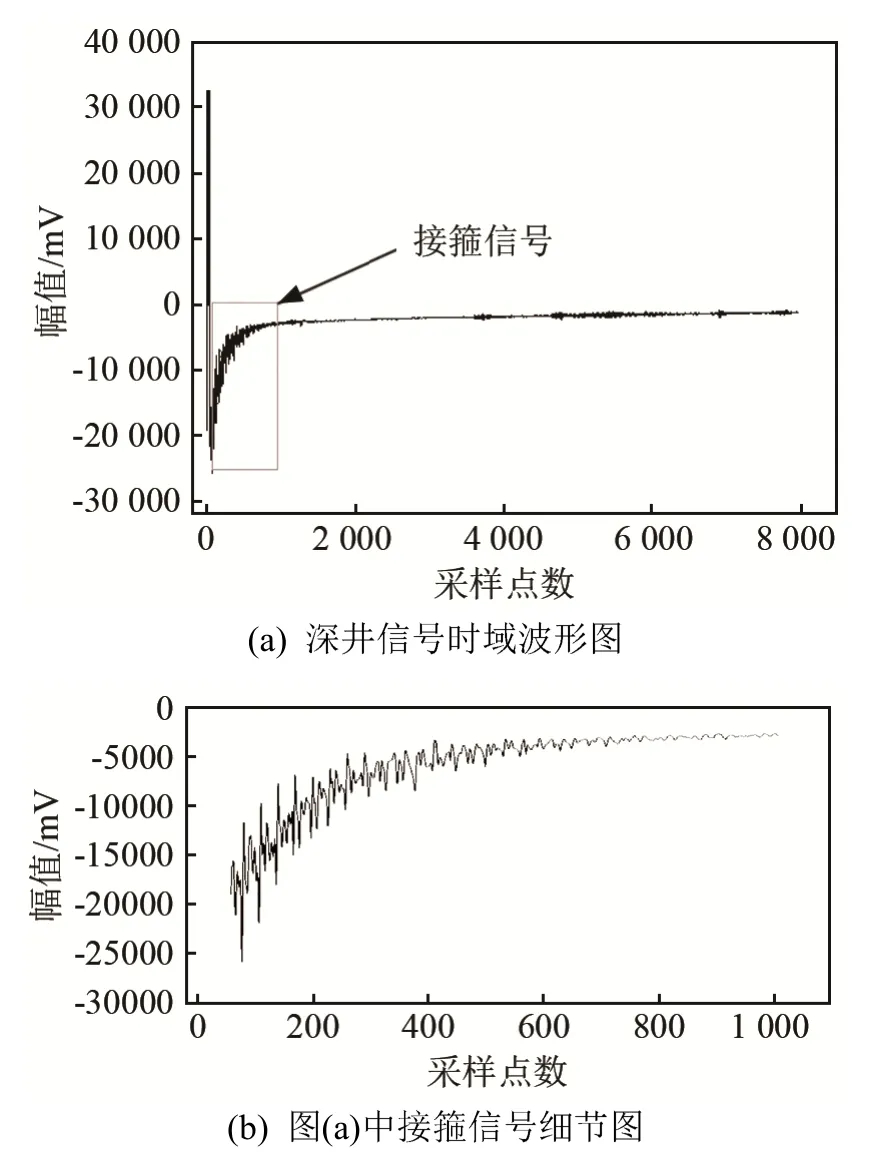
图7 深井信号及FFT和apFFT得到的接箍波段数据频谱Fig.7 The deep well signal and the spectrums of coupling wave data obtained by FFT and apFFT

根据接箍波峰所对应的采样序列号求出声波信号渡越每个接箍所对应的采样序列号的平均值：

则深井时域声速计算结果为

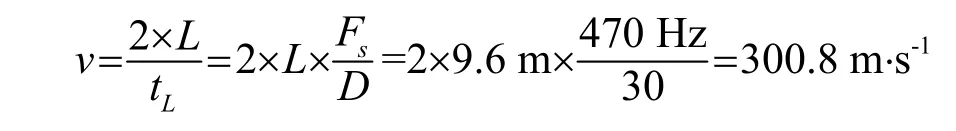
下面采用频谱分析法计算深井中的声速。

频谱分析法中，对接箍波段数据的145个采样点做FFT和apFFT，频谱图中展示出其频谱的一半即可，如图7(c)和图7(e)所示。

(1) FFT谱分析法

根据图7(c)所示的频谱图，检测各谐波频率所对应的采样序列号为 7、11、16、20、23，并根据各谐波频率所对应的采样序列号求出接箍波基频所对应采样序列号的平均值为

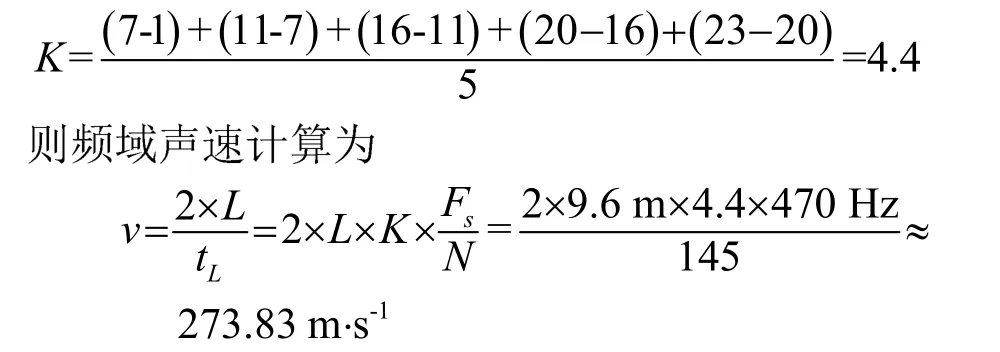
(2) apFFT谱分析法

根据图7(e)所示的频谱图，检测各谐波频率所对应的采样序列号为 7、11、15、20、25，并根据各谐波频率所对应的采样序列号求出接箍波基频所对应采样序列号的平均值为

由图7可以看出，通过传统FFT得到的频谱中，由于其频谱泄露较严重，导致有效谱峰的位置不易辨识。而通过全相位FFT得到的频谱，几乎没有频谱泄漏现象，谱峰更为规则且其位置易于识别，从而有利于接箍反射波频域特征的辨识与提取。根据有限的一段接箍波时域波形计算出的声速为300.8 m·s-1，通过apFFT谱分析法计算出的声速为 298.73 m·s-1，而根据 FFT谱计算出的声速为273.83 m·s-1，前两个值较为接近，再次验证了由apFFT法计算出的声速值更为准确。当估算更深层井中的声速时，时域法已不再适用，而基于apFFT的频域法可发挥较大的作用。此外，由于声速的大小与介质、温度、压力等因素有关，温度越低、压力越小，声速就越小。随着井深的增加，压力减小，因此深井中的声速较浅井也有所减小。

5 结 论

本文针对声波法测油井中接箍信号时域波形特征微弱的情况下不易计算声速的问题，提出频域分析法计算声速。而在接箍信号较弱时，基于FFT的声速计算方法误差较大，因此采用基于全相位FFT的声速计算方法。首先，在设定的已知声速下，模拟一组声波法测油井数据，采用 FFT和 apFFT两种频域分析法对接箍波进行频谱分析，并根据其频谱估算声速，然后以设定的声速为参考标准，对比两种估算方法的精度。通过实验验证与结果分析，可知apFFT能够有效改善传统FFT的频谱泄露问题，在抗噪性和稳定性方面更优，从而使基于apFFT的声速计算方法相比基于FFT的声速计算方法精度更高。最后，选取了两组分别来自浅井和较深井的现场测井数据，对其中的接箍波段数据采用时域法以及基于FFT和apFFT的两种频域法进行声速估算，根据估算结果发现，apFFT法所得结果与时域法所得结果更为接近，并在时域法无法估算时仍能进行有效估算，从而再次验证了apFFT谱分析法进行声速估算的优越性。这也为在更深井中接箍反射信号极微弱的情况下进行声速估算提供了一种有效的方法。