陆地靶场声定位系统布站图形优化方法
2021-05-10于国栋王春阳
于国栋,王春阳,张 月
(63850部队,吉林白城137001)
0 引 言
陆地靶场试验中,精确的测试结果对于武器装备的评定起着至关重要的作用。随着测试系统数量的增加和复杂性的提高,合理使用测试设备显得格外重要。
目前,利用声定位技术测量落点坐标的相关设备已在陆地靶场验收,并取得较好的效果。决定设备能否发挥其最大效能,主要取决于两个方面:高效的数据处理方法[1]和高质量的布站阵形结构[2]。自设备投入使用以来,经过不断研究探索,已总结出很多有价值的成果[3-6]。但查阅国内外文献后发现,目前针对声学设备布站阵形结构的研究成果较少,大多数基于光学设备和定位导航设备,只有文献[2]中有关于声定位设备布站阵形结构对定位精度影响的论述,但并未总结出度量布站阵形结构优劣程度的方法。
陆地靶场的声定位设备需要在弹丸落区周围布设一些探测器,来接收弹丸落地时产生的声信号。对信号进行处理,提取出爆炸信号到传感器间的时延差作为观测值,进行解算可以得到弹丸的落点坐标。根据声学设备的特性及使用方式,优化其布站阵形结构通常需要从两个方面进行考虑:探测器阵列的布站阵形和探测器的数量。合理的布站阵形可有效提高设备的测试精度及可靠性;除布站阵形外,探测器数量也会对测试结果产生一定的影响,使用过多的探测器,并不会明显提高测试精度,反而降低了系统的使用效率。
为能有效提高陆地靶场声定位系统的测试精度和使用效率,本文提出了一种布站阵形结构优劣的度量方法,并通过计算仿真数据和试验数据,验证了该方法的有效性和可行性。
1 原 理
1.1 声源定位原理及算法
声源三维坐标为(x, y, z),需要布设3个以上探测器才能得到声源的位置,设探测器数量为 n。如图 1所示,各探测器位置分别为(x1, y1, z1),为探测器接收到声源信号的时刻。以t1为基准,其他时刻与t1的差为Δ t12,Δt13,…,Δt1n,声速为c。
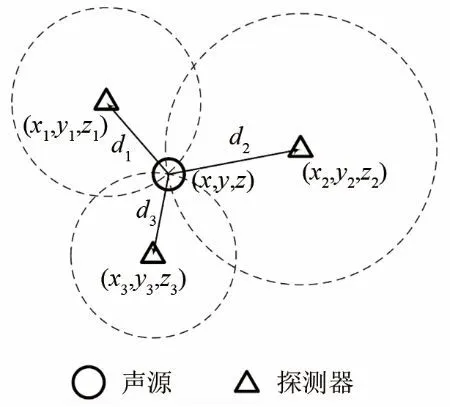
图1 声定位原理示意图Fig.1 Principle diagram of sound positioning
根据探测器与声源的几何关系,可构造如下误差函数:


由于陆地靶场试验场地较平坦,弹丸落点的高程与探测器阵列的高程差异较小。因此,文章中对布站阵形的分析均是基于二维平面,无高程元素,但计算方法相类似,不另做分析。
1.2 布站阵形结构优劣的度量方法

式中,λi为矩阵的特征值。当λi中有一个或者几个接近于0时,则Ui(i = 1 ,2,m)接近0。
虽然Ui可以直接反映布站阵形结构的几何特性,但不能确定阵形结构的优劣。主要原因为:一是Ui的大小与向量模有关;二是 U没有相对性。另一方面,对于观测矩阵B∈ Rm×n,一般m> n,仅考虑m=n是不全面的。
对于观测矩阵B∈ Rm×n,当m=n时,观测矩阵B的行向量为则:

此时,所有向量的模一样,U0为超平行多面体的最大体积,与理想结构下的超平行多面体体积相比,可作为衡量阵形结构优劣的依据[9]。因此,设向量组中范数最大的观测向量为b1,则:

当m> n时,为了计算方便,B分解成 B = Q1G,Q1是正交列满秩矩阵,G为行满秩矩阵。矩阵 G的行向量为,设g1为范数最大的行向量,则:

可以看出,E的范围为1≤ E ≤ ∞ 。显然,Um越接近U0,即E越小,阵形结构越好,相反,E越大阵形结构越差。当 E大于一定界限时(界限值根据具体情况决定),说明探测器组成的阵形结构非常差,严重影响设备的测试精度,使得设备的测试结果变得不可靠。
2 仿真与分析
优化布站方案通常从探测器组成的布站阵形和布设探测器的数量两个方面来考虑。
适合陆地靶场应用的布站阵形,优选有L型、U字型、||型、口字型、田字型五种,如图2所示。
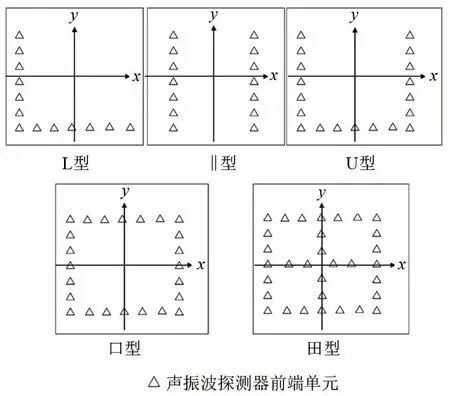
图2 五种布站阵形示意图Fig.2 Diagram of the five sensor layout patterns
2.1 布站阵形对观测结构的影响
为比较上述五种布站阵形,模拟了一组数据,在0 < x < 2 000 m ,0 < y <2 000 m范围内,以网格进行划分,间隔10 m,网格交叉点处作为弹丸落点。五种图形中探测器的位置如下:
(1) L型 : 范 围 为 :300 m < x<1 700 m ,300 m < y<1 700 m,间隔100 m,共29个探测器。
(2) ||型 : 范 围 为 :300 m < x<1 700 m ,300 m < y<1 700 m,间隔100 m,共30个探测器。
(3) U 型 : 范 围 为 :300 m < x<1 700 m,300 m < y<1 700 m,间隔200 m,共22个探测器。
(4) 口 型 : 范 围 为 :300 m < x<1 700 m,300 m < y<1 700 m,间隔200 m,共28个探测器。
(5) 田 型 : 范 围 为 :300 m < x<1 700 m ,300 m < y<1 700 m,间隔200 m,共40个探测器。
对网格交叉点处的仿真落点进行计算,得到所有落点的E。再统计所有落点的E的平均值和均方差,结果如图3和表1所示。
从图3和表1可以看出,五种布站阵形的E值平均值无明显差异,说明五种布站阵形对测试结果的影响无差别。但是,从E的均方差来看,田字型最优,L型最差,剩余三个图形差异不明显。出现这种情况的原因为:L型在控制区域的左上角、左下角及右下角结构较差,影响了其E的均方差;而田字型在x和y方向均有一定数量的探测器,并且这些探测器分布均匀,因此,即便有个别区域结构较差,也不会对E的均方差产生太大的影响。
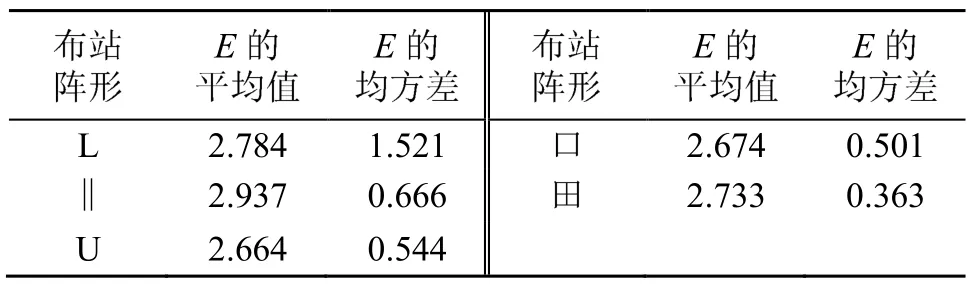
表1 五种布站阵形的仿真结果(整个区域)Table 1 Simulation results of five sensor layout patterns(whole region)


图3 五种布站阵形的仿真结果Fig.3 Simulation results of five sensor layout patterns
陆地靶场试验时,不需要对全部理论落区进行控制,往往存在一个关注区域,大多数弹丸会落入该区域,只有少数异常弹会出现在该区域之外,因此, 通常我们更关心关注区域处的测试精度。仿真试验中,将400 m < x<1 400 m ,400 m < y <1400 m区域设定为关注区域。对关注区域内的落点进行计算,并统计E的平均值和均方差,结果表2所示。
从表2可以看出,L型最优,||型最差,剩余三种无明显差异。出现这种情况的原因是:||型在 x方向上布设的探测器过少,因此在该方向上的结构较差,而其他四种图形在x和y方向上均布设一定数量的探测器,因此,结构相对较好。从E的均方差来看,U字型和口字型结构变化较平稳,田字型结构变化较剧烈,出现这种情况的原因是,田字型中间添加的十字型影响了结构的连续性。
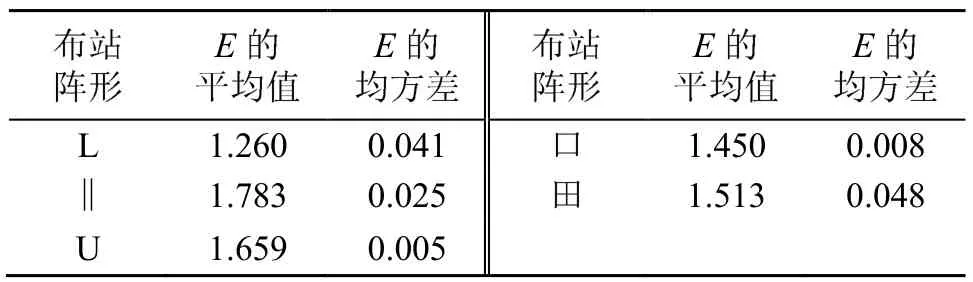
表2 五种布站阵形的仿真结果(关注区域)Table 2 Simulation results of five sensor layout patterns(region of interest)
通过上述分析,可以总结出如下结论:
(1) 布站阵形的选择,需要根据试验的具体情况决定。
(2) 布站方案倾向于考虑整个落区的观测结构,尽量避免使用L型布站,推荐采用U字型、口字型、田字型;当倾向于考虑关注区域的观测结构时,L型结构最好,||型最差,因此,尽量避免使用||型布站。
(3) 当落区环境较差,不易于布设过于复杂的图形时,可选择U字型或口字型。
2.2 探测器数量对观测结构的影响
模拟一组数据,在0 <x< 2 000 m ,0 <y< 2 000 m范围内,以网格进行划分,间隔10 m,网格交叉点处作为弹丸落点,其中,400 m <x<1 400 m ,400 m <y<1 400 m被设定为关注区域。采用L型布站,在每条边上逐步增加探测器数量,设每条边探测器数量为 k。分别计算整个区域和关注区域中的落点,结果如图4所示。

图4 L型布站阵形受探测器数量的影响Fig.4 The influence of the number of sensors on the“L” type sensor layout pattern
不难看出,当k=2时,E的平均值和均方差均较大,即此时的结构最差。当k=3时,E的平均值和均方差明显降低,随着探测器数量的增加,图形结构变化趋于平缓。对于整个区域,E的均方差逐渐减小,直到k=15时,趋于平缓;对于关注区域,E的均方差在k=2时最大,然后迅速减小,随着探测器数量的增加,E的均方差逐渐增大,直到k=18时,趋于平缓。
采用口字型布站,用同样的方式进行计算,得出的结果如图5所示。
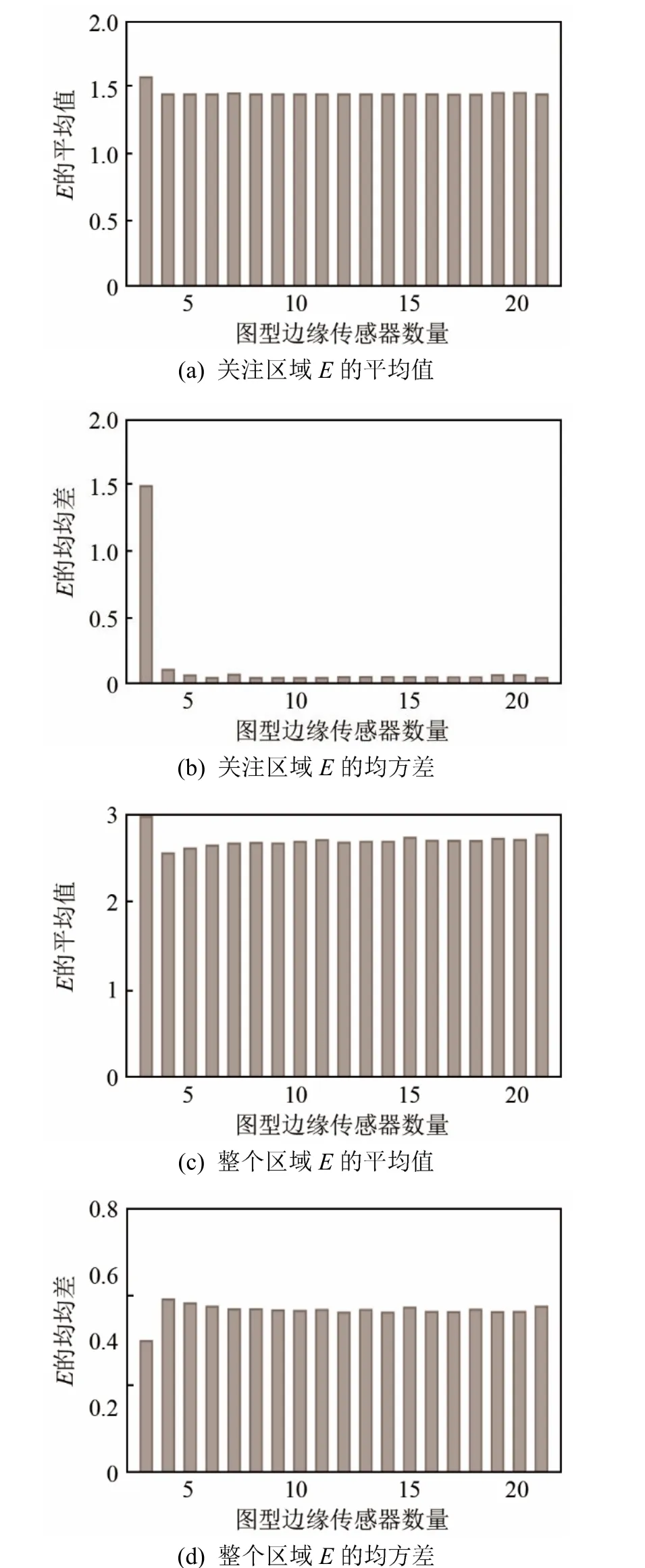
图5 口字型布站阵形受探测器数量的影响Fig.5 The influence of the number of sensors on the“口”type sensor layout pattern
可以看出,对于整个区域,当k=2时,E的平均值最大,而均方差最小。当k=3时,E的平均值稍有下降,随着探测器数量的增加,图形结构变化趋于平缓;当k=3时,E的均方差相对于k=2时有所提高,随着探测器数量的增加,E的均方差略有下降,直到k=8时,趋于平缓。对于关注区域,当k=2时,E的平均值和均方差最大,当k=3时,E的平均值略有降低,随着探测器数量的增加,趋于平缓,而E的均方差在k=2时最大,当k=3时,E的均方差迅速降低,随着探测器数量的增加,趋于平缓。
通过上述分析,可以总结出如下结论:
(1) 探测器的布站数量,需要根据试验的具体情况决定。
(2) 不同的布站阵形,探测器数量对观测结构的影响是不同的。
(3) 当L字型布站时,每条边应布设至少3个探测器,当布设超过 10个以后,再增加探测器数量,对测试结果不再产生影响。
(4) 当口字型布站时,每条边应布设至少3个探测器,当布设超过5个以后,再增加探测器数量,对测试结果不再产生影响。
3 试验算例与分析
3.1 布设图形对定位精度影响
为了进一步验证本文方法的有效性,设计了一个模拟试验的场景,采用爆竹代替弹丸产生声源,探测器选型一致,可假设时延估计精度一致。试验当天天气晴朗,空气湿度较低,无风,在一块相对平坦的场地,分别以L型、U字型、||型、口字型、田字型五种方式布设探测器阵列,间隔为100 m,在每个阵列内部均匀放置 15个爆竹,在外部均匀放置 10个爆竹,用北斗定位设备精确测量其位置坐标,定位精度为2 cm。依次点燃爆竹,采集声波数据,并采用1.1小节的计算方法对爆竹位置进行定位解算,将解算结果与北斗设备的测量结果进行比对,结果如表3所示。
表3中均方根误差采用贝塞尔公式进行计算,其计算公式为

表3 布设图形对定位精度影响Table 3 The effect of the sensor layout pattern on positioning accuracy

式中:Mx,My分别为x,y方向上的均方根误差,Δx,Δy为解算结果与北斗测量结果在x,y方向上的坐标差,n为声源个数。
从表3可以得出,当声源位于阵列内部时(即位于关注区域内),L型的误差较小,||型及U字型的误差较大;当声源位于阵列外部时,L型的误差较大,其他四种方式相差较小。这与2.1小节的分析结果一致。
3.2 探测器数量对定位精度影响
文章选用L字型布站方式进行验证,图形的每条边探测器数量k分别为2、3、5、8、10,试验方法和步骤与3.1小节一致,结果如表4所示。

表4 探测器数量对落点坐标精度的影响Table 4 The effect of the number of sensors on positioning accuracy
从表4可以得出,当声源位于阵列内部时(即位于关注区域内),k=2,误差较大,随着探测数量的增加,定位精度明显提高;当声源位于阵列外部时,k=2,误差达到10 m,当k=3时,精度明显提高,在基础上进一步增加探测器数量,则精度无明显提高,这与2.2小节的分析结果一致。
4 结 论
本文提出了一种度量布站阵形结构优劣的方法。该方法基于观测向量组空间几何特性分析理论,从探测器组成的布站阵形和布设探测器的数量两个方面来度量布站方案的优劣,可为设备布站方案设计提供理论依据,能有效提高设备的测试精度和使用效率。
