基于VMD-PNN的砂轮钝化声发射检测

龚子维，刘希强，张仲宁，杨 京，程建春，刘翔雄

(1. 南京大学声学研究所，江苏南京210093；2. 人工微结构科学与技术协同创新中心，江苏南京210093；3. 华辰精密装备(昆山)股份有限公司，江苏昆山215337)

0 引 言

声发射(Acoustic Emission, AE)是指材料受到外力或者内力作用，发生塑性变形或断裂，以瞬态弹性波的形式释放应变能的现象[1-2]。利用声发射检测磨削加工过程中砂轮的钝化状态，相比于其他间接检测方法具有环境噪声易分离、可选特征参数较多，灵敏度高、响应速度快等特点[3]，近年来声发射检测在刀具钝化状态检测中得到广泛应用。文献[4]研究了单磨粒模型中磨粒磨损过程及声发射产生机理；文献[5]建立了砂轮磨削的简化理论模型，推导出塑性功功率与剪切力、接触面积以及切入深度等加工参数的关系，声发射能量大小与砂轮钝化存在相关性。

与其他刀具类似，砂轮钝化程度随磨削时间推移而增加，文献[6-7]分别用加工材料单位去除量所需时间或能量来表示砂轮钝化程度，加工过程中砂轮从修整结束到下一次修整之前可以分为初期钝化、中期钝化和严重钝化三个钝化阶段。初期钝化阶段砂轮刚经过修整，磨粒较为锋利，发生的变化以磨粒破碎为主，这种钝化会产生新的切削刃，即“自锐现象”，对磨削能力影响较小；在中期钝化阶段，磨粒发生塑性变形，表面逐渐磨平，与加工材料接触面积增大，砂轮钝化程度平稳上升；到了严重钝化阶段，更多磨粒开始出现断裂、脱落，砂轮加速钝化，需要及时修整[6]。图 1为磨削过程中砂轮钝化程度变化曲线。

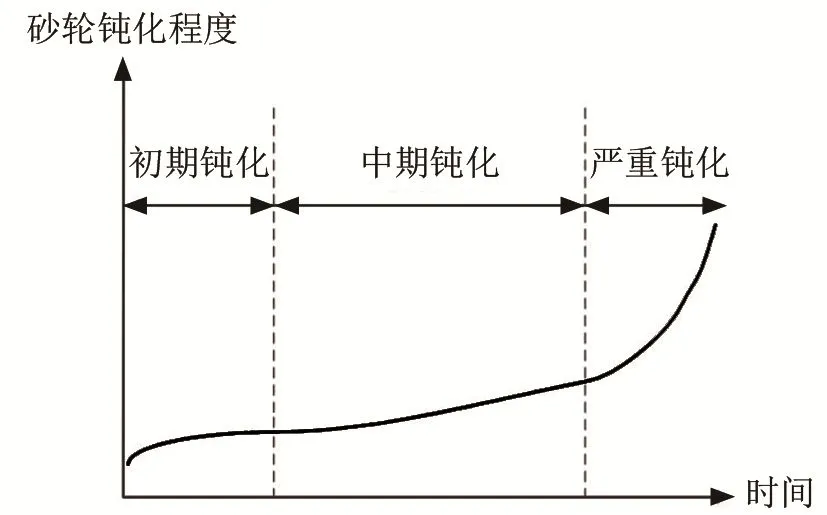
图1 砂轮磨削钝化曲线Fig.1 Grinding wheel blunting curve

利用声发射信号来检测砂轮的钝化状态，首先需要对采集到的原始信号进行去噪处理，声发射信号的频率主要分布在100～500 kHz，其他为低频的摩擦噪声和较高频的电气噪声。目前主要采用的信号处理方法包括小波变换(Wavelet Transform, WT)、经验模态分解(Empirical Mode Decomposition,EMD)等。WT方法利用窗函数平移将原信号分解成若干小波分量，这种方法需根据信号特点选定小波基，易产生异常谐波。EMD方法属于递归分解，根据信号本身的特点将一段信号分解成一组本征模态函数(Intrinsic Mode Function, IMF)，适用于非线性、非平稳信号。针对EMD方法易产生包络线误差累积、模态混淆及端点效应等问题，Dragomiretskiy等[8]提出变分模态分解(Variational Mode Decomposition, VMD)，该方法具有完备的数学理论基础，克服了小波分解需定义小波基的问题，通过求解约束变分模型将信号分解为指定数量的本征模态分量，能够避免端点效应、抑制模态混叠，且分解较为彻底。

对分解后的分量进行筛选并重构得到声发射信号后，还需要提取声发射信号中能够表征砂轮钝化状态的特征参数。为探究砂轮钝化程度和声发射信号特征参数的关系，文献[9]通过实验将声发射的振铃计数和均方根值(Root Mean Square, RMS)两个特征参数与砂轮钝化状态联系起来；文献[10]提取声发射 RMS信号，利用声发射频域信号频谱矩心特征参数来表征砂轮钝化状态；文献[11]证明RMS和能量计数两个统计数据含有砂轮表面状态的重要信息；文献[12]将功率比(Ratio of Power, RoP)引入砂轮磨损评估中；文献[13]提取了声发射信号的幅度、振铃计数、能量计数等八个特征参数构建训练集对砂轮钝化状态进行识别。以上方法基本实现了对砂轮钝化状态的识别，但均未对不同特征参数的作用进行量化比较，没有系统性衡量声发射信号多种特征参数对砂轮钝化状态的识别效果。

特征参数与砂轮钝化状态的具体对应关系数学模型目前较难建立，国内外相关研究通过训练神经网络来识别砂轮钝化状态，而声发射信号本身存在一定的波动，会影响识别的准确性。概率神经网络(Probabilistic Neural Network, PNN)利用密度函数估计方法输出识别结果，对于非线性数据也能保持较高精度，适用于处理非线性、非平稳的磨削声发射信号。

综合以上因素，本文提出一种基于VMD-PNN进行声发射信号处理和砂轮钝化状态识别的方法。利用VMD快速精确地得到声发射信号，选取典型特征参数构建多维特征向量数据集，通过 PNN网络建立磨削声发射信号与砂轮钝化状态的关系。经过测试，该方法可以较为准确识别砂轮钝化状态，并能横向对比不同特征参数的检测效果。

1 方法理论

1.1 变分模态分解(VMD)

VMD算法基于维纳(Wiener)滤波和希尔伯特(Hilbert)变换方法，能够将信号自适应分解为 k个稀疏的本征模态函数(IMF)，第k个本征模态函数表示为

K为分解层数，然后利用交替方向乘法算子算法(Alternate Direction Method of Multipliers, ADMM)求解式(5)的最优解，在频域内迭代更新uk、ωk和λ。

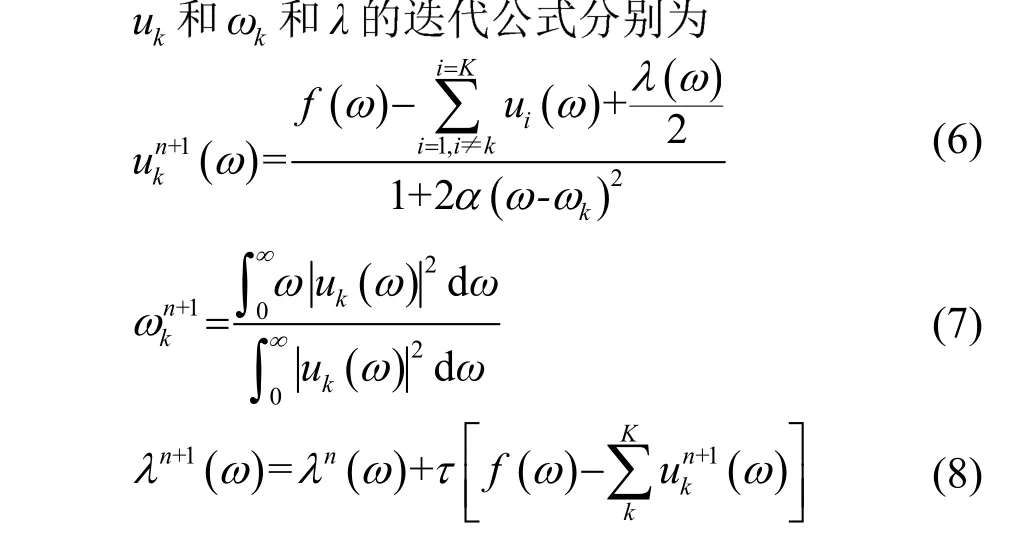
最后重复式(6)～(8)，直到满足式(9)中的终止条件，并输出最后结果。

式中：ε为设定的终止参数。

1.2 声发射特征参数选取

声发射信号是有许多声发射事件(AE Hit)组成的，从波形首次越过门限值开始，直到落回门限值以下并且一段时间内(该时间设置为撞击定义时间)不再升到门限值以上，定义为一次AE Hit。一个典型的AE Hit波形如图2所示。

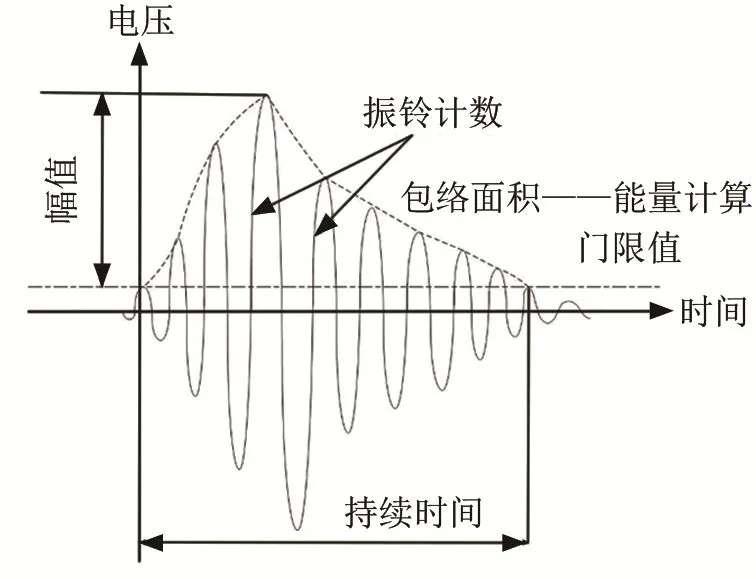
图2 典型声发射信号波形图Fig.2 Waveform of typical acoustic emission signal

对于每次AE Hit，有多种常用特征参数来进行描述。幅度(Amplitude)指AE Hit达到的最大振幅；持续时间(Duration)指一次AE Hit从开始到结束的间隔；振铃计数(ring-down counts, 记为C)，表示一次AE hit越过门限的震荡次数；能量计数(SE)，表示一个AE hit的波形包络面积；均方根值(RMS)，指的是AE hit信号幅度的均方根值，表达式为

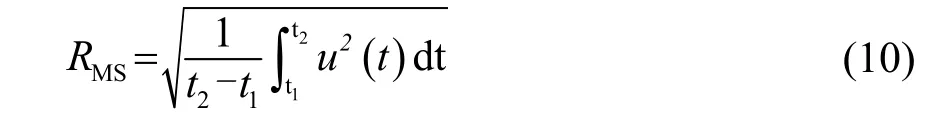
式中：u( t)为信号幅度，以上特征参数都应用于描述单次AE Hit，在一段声发射信号中，需计算所有AE Hit对应特征参数并求均值作为该段声发射信号的特征参数，因此这些特征参数不能衡量AE Hit的密度和声发射信号整体状况。

文献[14]提出一种通过功率比来评价声发射信号的特征量，声发射功率比：

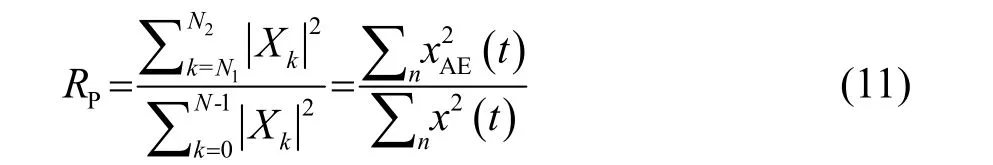
式(11)是RP频域和时域的两种表示方法，N1和N2为声发射的频率范围，在本文中RP含义为声发射信号功率与原始信号功率之比。RP可以排除信号随时间变化引起的功率值整体波动影响，适用于衡量声发射信号在时域的变化规律。

参考能量计数的定义原理，用希尔伯特变换对信号求包络，在一段信号中，声发射分量包络能量和原始信号包络能量的比值定义为声发射包络能量比REE：

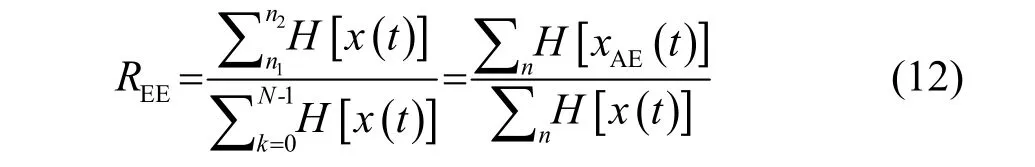
式中： xAE(t)是信号x( t)经过分解后的声发射分量,H[ x ( t)]是信号的希尔伯特变换。

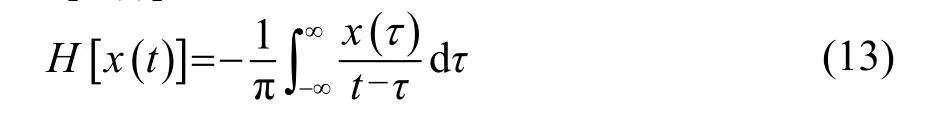
REE含义为声发射信号能量占比，这里的声发射能量是一种结合声发射信号特征定义的包络能量，含义为信号检波包络线下的面积，量纲为mV·ms，与物理意义上的能量不同。

特征参数选取是声发射检测的重要环节，以上声发射特征参数可以分为两类，一类是对单次 AE hit进行评价，分别从信号电平、时间和包络能量(电平×时间)三个维度进行衡量，在计算时需对一段信号所有AE hit分别计算并求平均值；另一类为声发射信号与原始信号的功率或包络能量比值，是对声发射信号进行整体衡量，上文所提到的声发射特征参数分类如表1所示。其中幅度和持续时间易受异常声发射事件影响，波动较大，结合此前相关研究基础，本文选取C、SE、RMS、RP和REE作为砂轮钝化状态识别参考特征参数。

表1 声发射特征参数分类Table 1 Classification of AE characteristic parameters

1.3 概率神经网络(PNN)

概率神经网络是一种建立在径向基(Radial Basis Function, RBF)网络的基础上，基于贝叶斯决策理论，结合密度函数估计方法的神经网络[15]。概率神经网络的结构如图3所示。

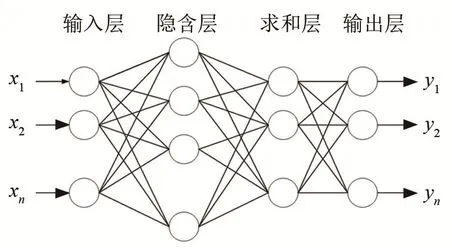
图3 PNN神经网络结构Fig.3 PNN neural network structure

结构共分为四层，第一层为输入层，接收训练数据集的值，神经元个数与输入向量长度相等，并

传递给第二层。第二层是隐含层，该层接收输入层的数据，并计算输入向量与中心的距离，输出一个标量，第i类模式的第j神经元的输入输出关系为

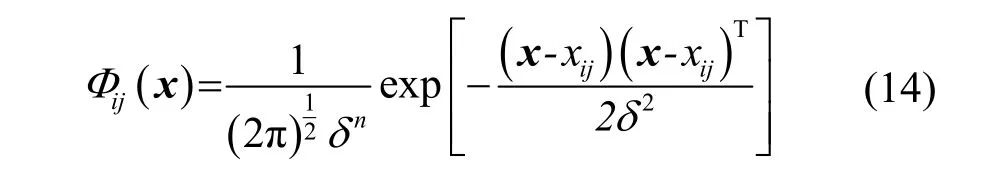
2 实验与结果分析

2.1 实验系统搭建

搭建声发射检测及砂轮钝化状态识别实验系统，包括三个组成模块，如图4所示。

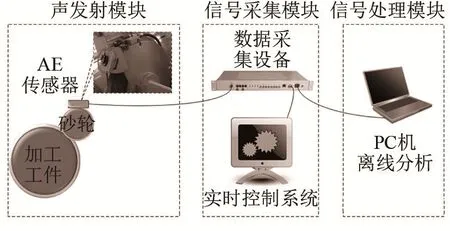
图4 声发射检测实验系统Fig.4 Experimental system for acoustic emission detection

砂轮选用 36粒绿色碳化硅砂轮，线速度为42 m·s-1，进刀量为0.03 mm；加工工件为合金铸钢；传感器为全接触式AE传感器，固介灵敏度较高，固定在磨床砂轮外壳上，响应范围为 0～3 MHz；AE传感器接收到的信号由安捷伦u2331数据采集设备采集，存储为二进制文件，再通过计算机进行信号分析处理。

2.2 VMD参数设定

信号处理的关键是利用VMD方法对原始信号进行分解得到声发射信号，VMD有两个重要参数α和K，α是惩罚因子，决定分解出每个分量的带宽限制，通常取默认值2 000；分解层数K的确定方法有多种，这里采取峭度判别法。相比于噪声信号，声发射信号波形陡峭，峭度值较大。逐步增大K，观察每个分量的波形和峭度，直到出现峭度值较小的非声发射分量为止，此时分解层数为适宜的K值，取其中峭度较大的分量重构，即得到声发射信号。VMD各模态的中心频率及峭度分布如表2、3所示。VMD 5层分解的IMF波形及频谱图如图5所示。

从表2、表3及图5观察到，随着分解层数K的增大，各分量的中心频率基本保持不变，在分解层数达到5时出现中心频率大于1 000 kHz而峭度较低的电气噪声分量，故分解层数K定为5，并判断IMF2、IMF3和IMF4是声发射信号分量，将这三个分量重构即得到所需的声发射信号。

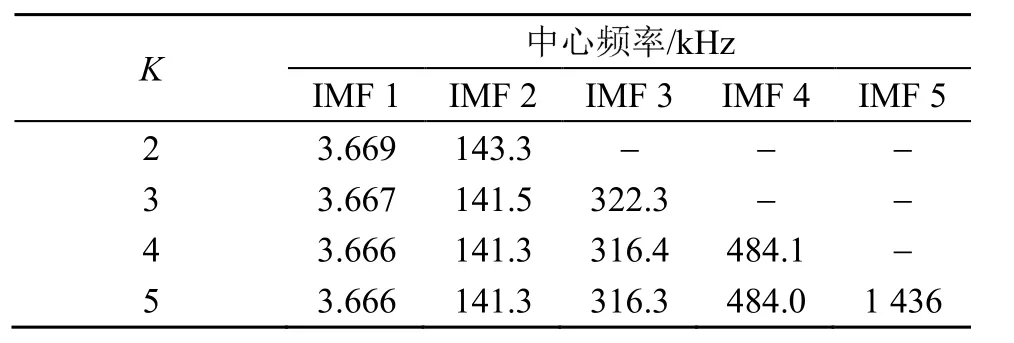
表2 VMD分解各模态中心频率分布表Table 2 Modal center frequencies of VMD decomposition

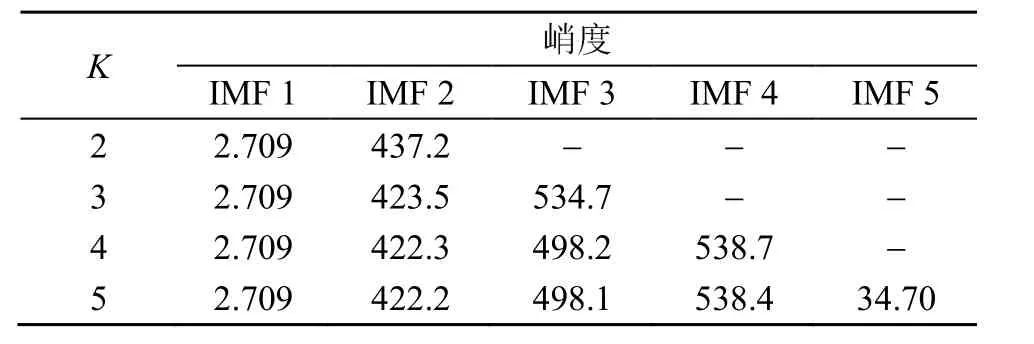
表3 VMD分解各模态峭度分布表Table 3 Modal kurtosis distribution of VMD decomposition

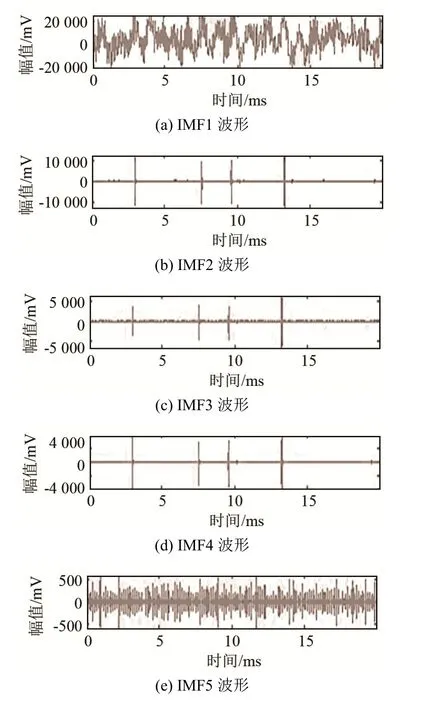
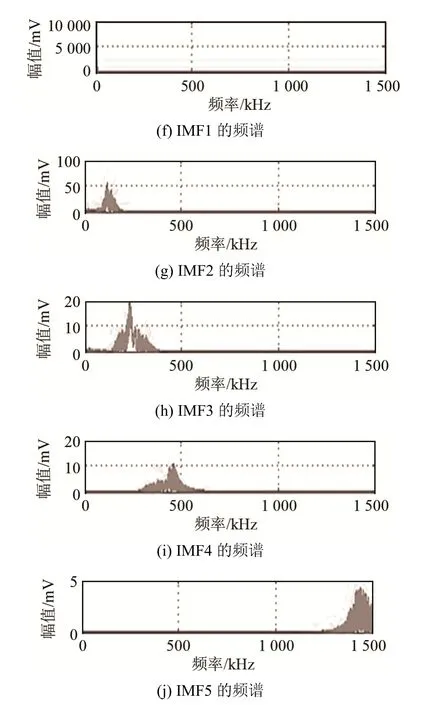
图5 VMD 5层分解IMF波形图及频谱图Fig.5 IMF waveforms and spectrums of 5 layer VMD decomposition

读取三段已标记砂轮钝化状态的信号数据波形文件并进行5层VMD分解，取IMF2、IMF3和IMF4进行重构，观察不同砂轮钝化状态下原始信号和声发射信号波形。图 6～8分别为初期钝化、中期钝化、严重钝化三个阶段的原始信号和 VMD分解后重构的声发射信号波形图及对应频谱。

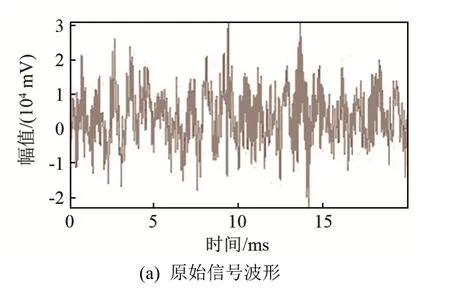
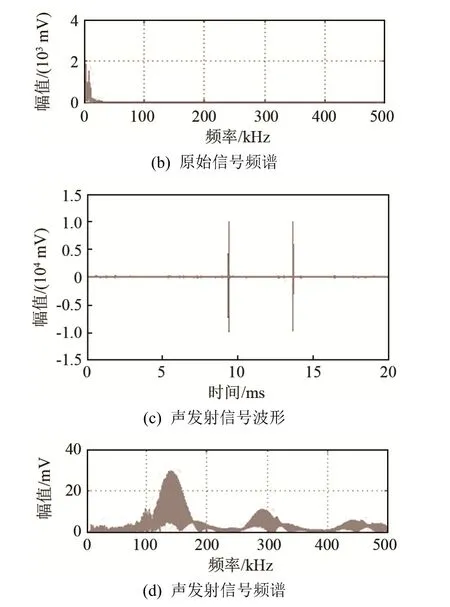
图6 初期钝化原始信号与声发射信号波形及频谱图Fig.6 The waveforms and spectrums of the original and the VMD reconstructed AE signals in initial blunting state

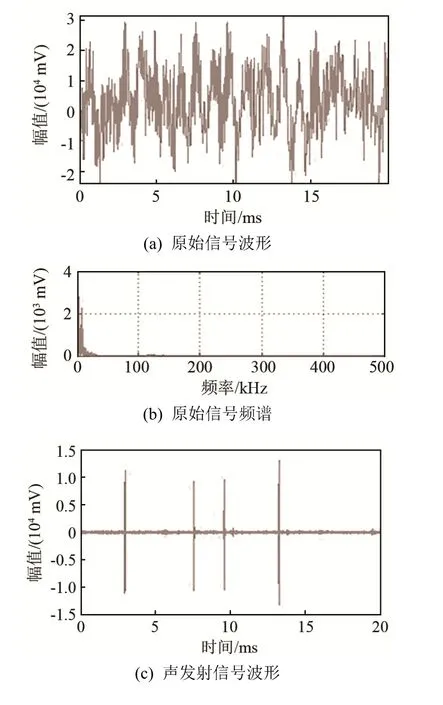
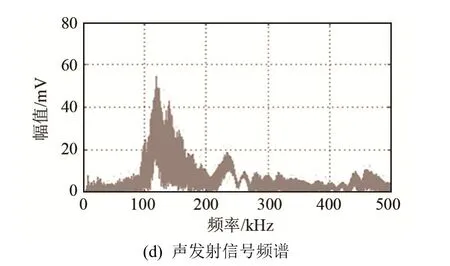
图7 中期钝化原始信号与声发射信号波形及频谱图Fig.7 The waveforms and spectrums of the original and the VMD reconstructed AE signals in intermediate blunting state

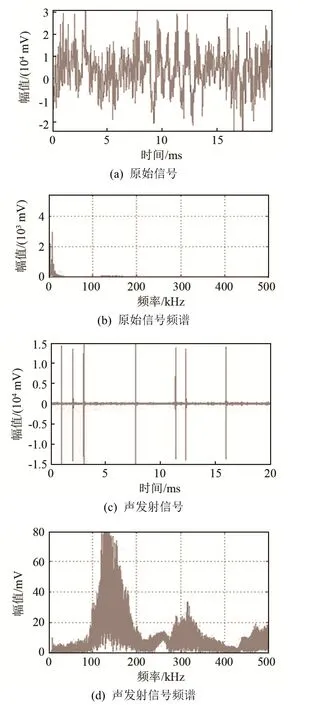
图8 严重钝化原始信号与声发射信号波形及频谱图Fig.8 The waveforms and spectrums of the original and the VMD reconstructed AE signals in severe blunting state

可以看出，磨削加工过程中砂轮处于初期钝化阶段时，声发射事件强度较弱，分布稀疏，20 kHz以上频段幅值较小；砂轮进入中期钝化阶段以及严重钝化阶段，单次声发射事件强度增大，声发射信号频谱幅值增大，故单位时间内声发射信号与原始信号的能量比也大幅增加。

2.3 数据集训练与识别结果分析

信号处理模块的全过程如图9所示，取磨削过程中已明确砂轮钝化状态的初期钝化信号40 s，中期钝化信号40 s，严重钝化信号20 s。对信号分别进行分帧处理，以 0.1 s为一帧，对每帧信号进行VMD分解、重构，得到1 000帧声发射信号。设定门限值为 300 mV，计算每帧声发射信号所有正常声发射事件的C、SE、RMS，并在一帧内求平均值得到平均C、平均SE、平均RMS、对每帧声发射信号进行整体计算得到RP和REE，共五个特征参数，构建一组五维特征向量数据集作为训练集，将训练集作归一化处理后输入PNN网络中训练。图9中将C、SE、RMS、RP、REE5个特征参数分别标注为①，②，③，④，⑤。

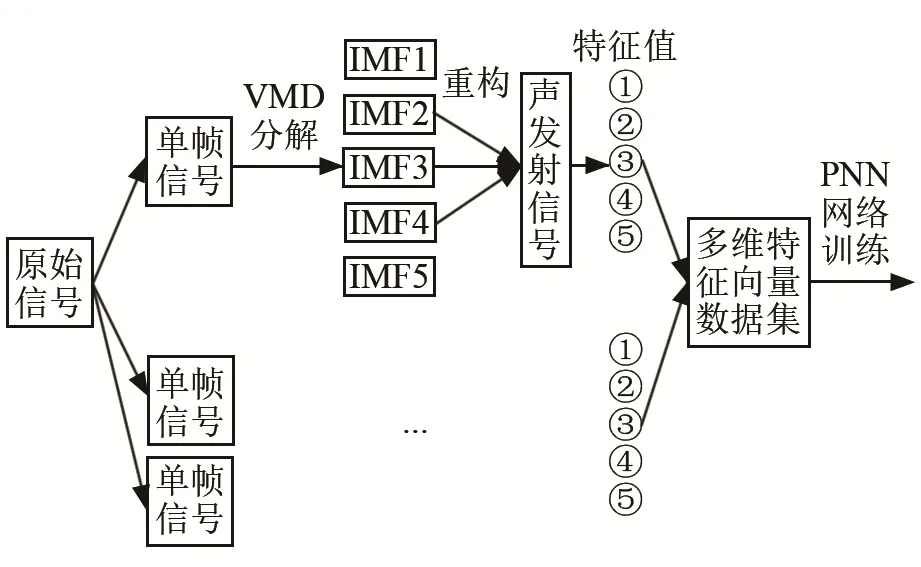
图9 多维特征向量数据集的构建过程Fig.9 Construction process of multi-dimensional characteristic vector dataset

改变信号分帧的起始位置，将训练集每帧信号后移0.05 s，帧长依然为0.1 s，得到的数据集与训练集是同一段信号因不同分帧方法所得，因此被认为是独立同分布的。将该数据集作为测试集，随机取三种状态各80、80、40帧，共200帧进行测试。

测试结果用混淆矩阵表达，如图 10所示，初期钝化状态、中期钝化状态和严重钝化状态分别被标记为类别1、2和3。同时利用五种特征进行训练和测试，整体识别准确率为94.5%，多次重复测试集取样过程，平均准确率维持在94%以上，且严重钝化状态对应的数据均能被正确判定为严重钝化。可以认为该神经网络经过训练后能够根据特征参数对砂轮钝化状态进行识别，并对严重钝化状态作出准确预警。

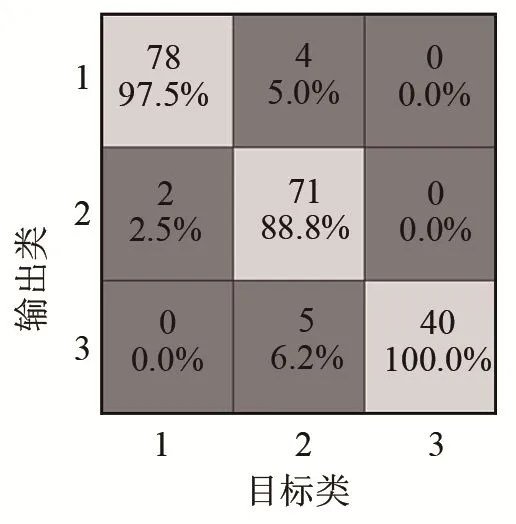
图10 混淆矩阵，砂轮钝化识别结果Fig.10 Confusion matrix and the identification result of grinding wheel blunting state

为评估该神经网络的泛用性，取另一段加工材料为合金锻钢支承辊的400 s连续磨削加工信号，设定帧长为0.1 s，帧移为1 s，即用每1 s信号中间0.1 s的特征参数来表征这1 s的砂轮状态。得到该段连续磨削加工信号的数据集作为连续信号数据集，图 11为该数据集的五维特征参数变化图。对连续信号数据集作归一化处理并输入已通过此前训练集训练好的PNN网络，得到识别结果如图12所示。连续信号数据集被清晰分成了三种钝化状态，不同颜色代表不同钝化状态，且随时间推移存在阶段性变化。在两个钝化状态之间存在短暂的过渡态，根据加工要求和材料特点，当连续若干帧信号有一定帧数信号被识别为严重钝化信号，可认为砂轮已经进入严重钝化状态，此时需要对砂轮进行修整。本文方法应用在其他加工工件上依然能够对砂轮钝化状态进行有效识别。

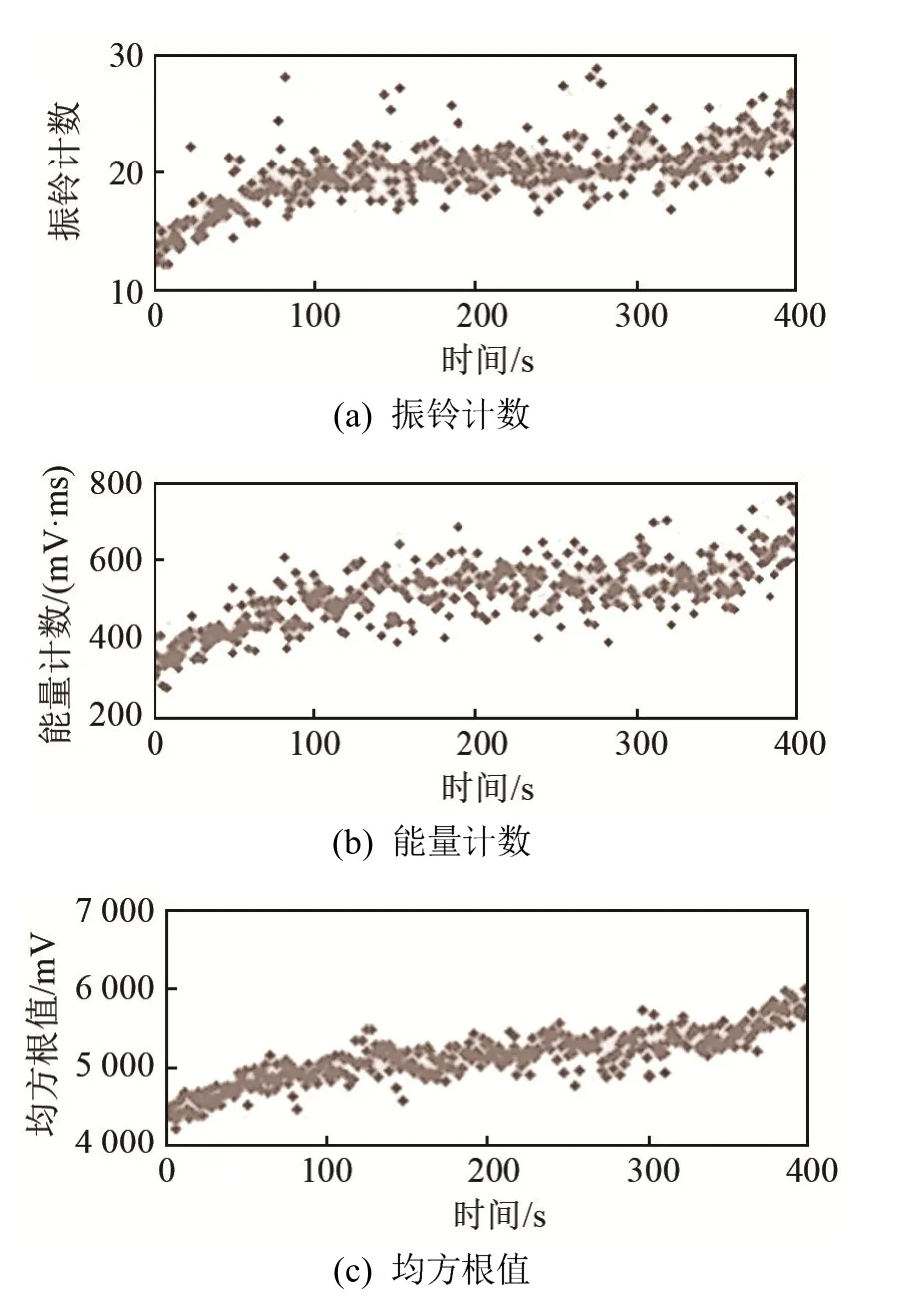
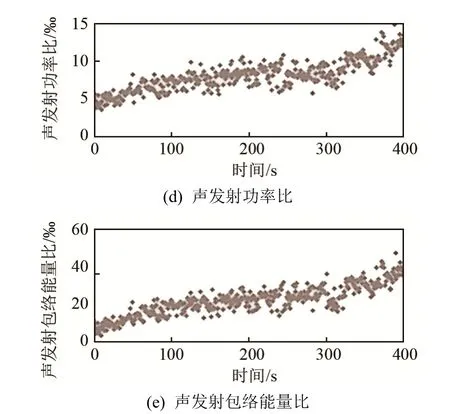
图11 连续磨削加工信号的5维特征参数数据集随时间变化图Fig.11 Variations of the 5D characteristic parameter dataset of continuous grinding signal with time

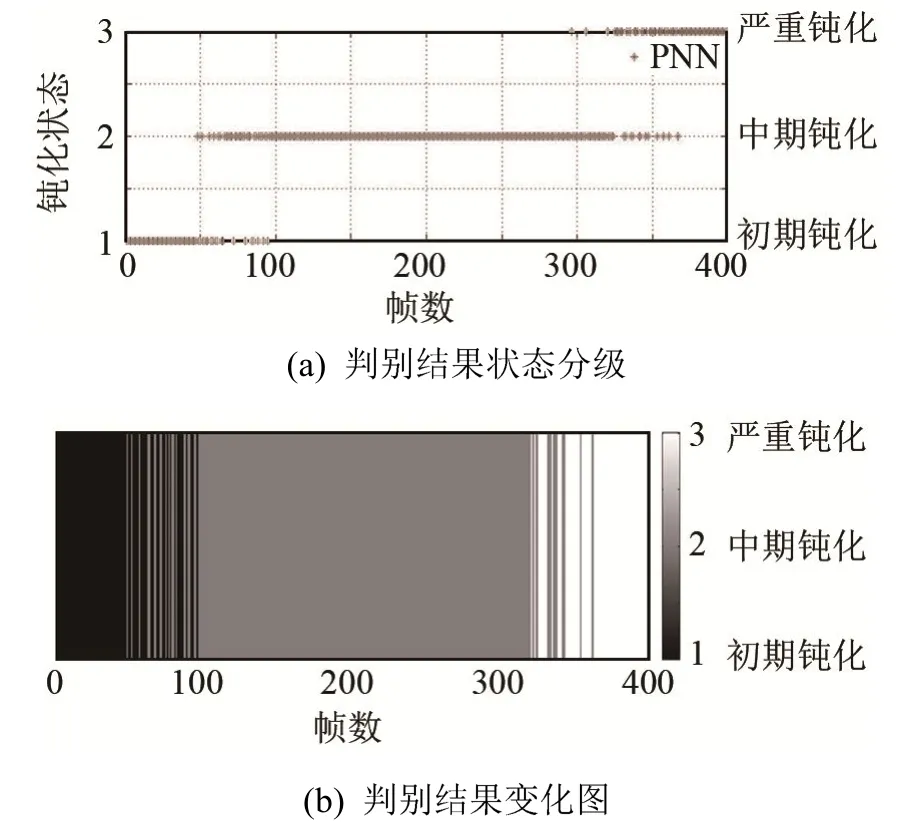
图12 砂轮钝化状态判别结果Fig.12 Identifying results of grinding wheel blunting states

2.4 不同特征参数识别准确率比较

探究不同特征参数对于识别准确性的影响，对特征参数进行分组，分组采用部分特征参数进行训练。5种特征参数分别标注为①，②，③，④，⑤，按表4分为15种组合方式。

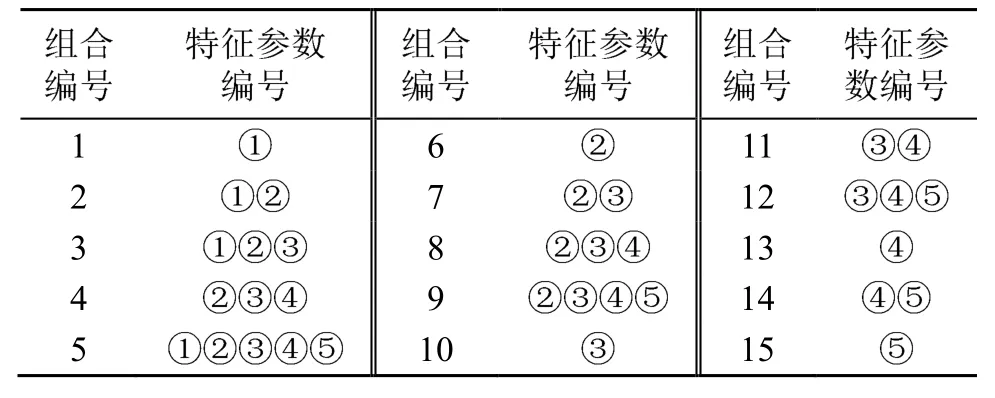
表4 特征参数分组表Table 4 Grouping table for characteristic parameters

对不同特征参数组合的训练集和数据集分别进行训练与测试，结果如图13和表5所示。其中，组合5因为同时用到了五种特征参数准确率最高。单个特征参数的识别准确率中，组合 10(RMS)的准确度最高，达到 91.0%；其次是组合 15(REE)和组合 13(RP)，单个特征参数的准确度达到 88.0%和85.5%。

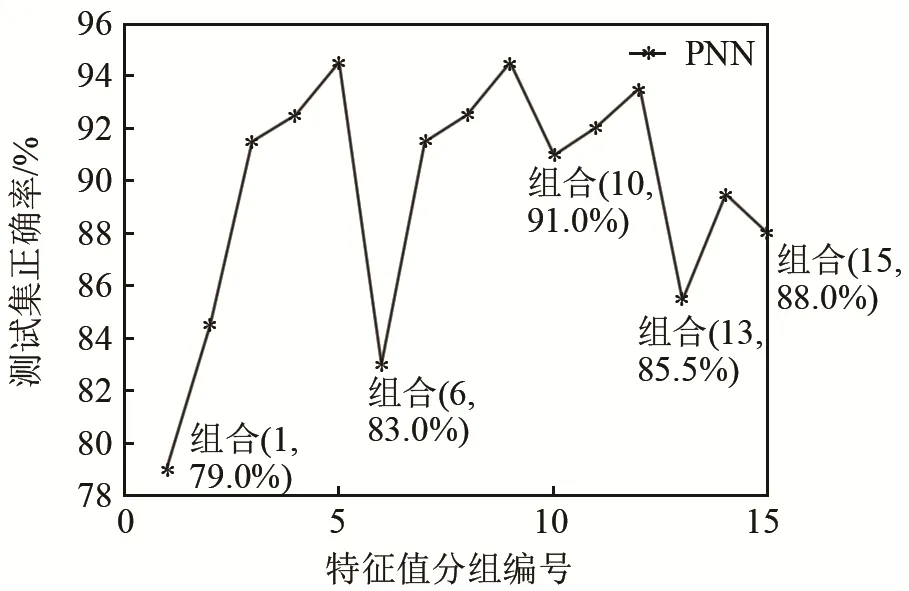
图13 特征参数组合测试正确率对比Fig.13 Comparison of correct rates between different characteristic parameter combination tests

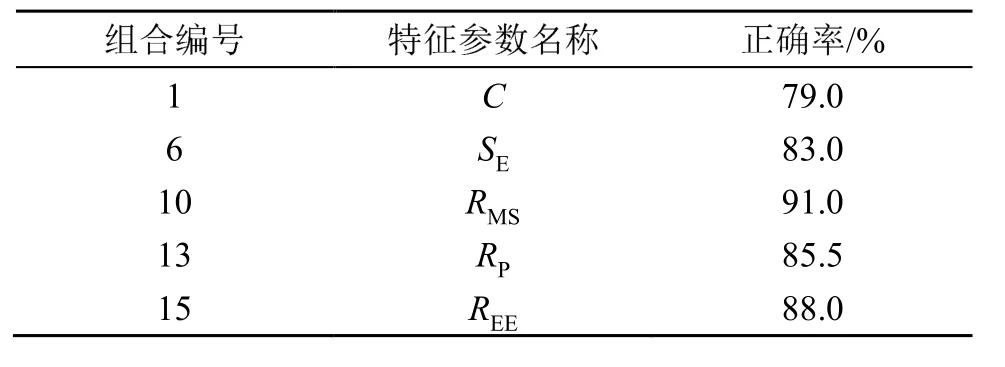
表5 特征参数单独训练测试结果表Table 5 Test results of individual characteristic parameter training

由此可得，不同声发射特征参数对砂轮钝化状态识别效果存在差异，使用多个特征参数的测试准确率高于使用其中部分特征参数，RMS、REE等典型特征参数与砂轮钝化状态相关性较强。

进一步探究两类声发射特征参数在不同钝化阶段的识别准确率差异，对比组合3和组合14，结果如表6。

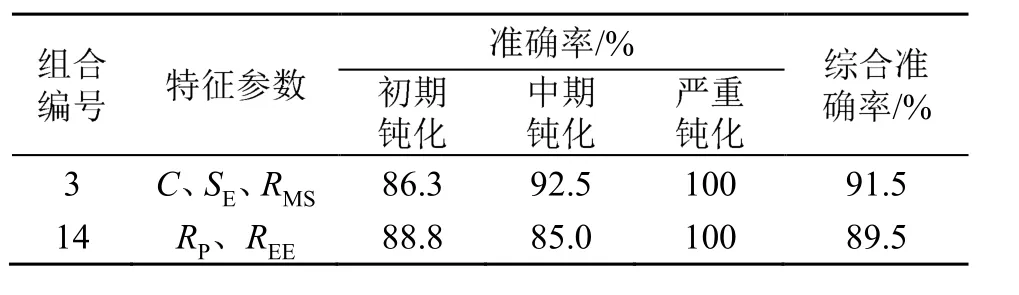
表6 两组特征参数在不同钝化阶段的识别准确率Table 6 Identification accuracy of two groups of characteristic parameters in different blunting stages

组合3特征参数(C、SE和RMS)衡量单次AE Hit强度变化，组合14特征参数(RP和REE)整体衡量声发射信号能量大小。从砂轮钝化原因来看，初期钝化主要是磨粒的破碎，AE hit密度增加而单次AE hit强度变化较小；中期钝化以磨粒磨损和塑性变形为主，磨削力和接触面积增大，AE hit强度有明显增加，使得第一类特征参数(组合1)在中期钝化阶段识别准确率高于初期钝化阶段；严重钝化阶段 AE hit强度和AE hit密度都大幅增加导致区分明显，两组识别准确率都很高。由此可知，声发射特征参数变化与砂轮钝化原因存在对应关系，通过针对性选取典型特征参数可以较准确地识别砂轮在特定阶段的钝化情况。

3 结 论

本文利用VMD方法，将磨削加工过程中产生的声发射信号分离出来，保留了声发射信号的主要特征并避免了噪声干扰。声发射特征参数变化存在一定的波动性，PNN能够较为准确地将特征参数对应到砂轮的不同钝化状态，测试准确率较高(94.5%)，且经过泛用性评估，实现了对砂轮钝化状态的识别和严重钝化状态预警。

声发射信号特征参数的选取是影响识别准确率的关键，本文在声发射检测相关研究基础上对特征参数进行归类，参考声发射能量的定义提出声发射包络能量比(REE)，共选取5个典型特征参数，通过分组训练并比较测试准确率的方式，证实了所选特征参数对砂轮钝化状态有较高的识别准确率，并验证了典型特征参数变化与砂轮不同钝化原因存在相关性，可为实际声发射检测特征参数的选取提供参考。