复合共鸣腔Janus宽带换能器

伊子旭，莫喜平，柴 勇,3，刘永平,3

(1. 中国科学院声学研究所，北京100190；2. 中国科学院大学，北京100190；3. 北京海洋声学装备工程技术研究中心，北京100190)

0 引 言

随着海洋研究的逐渐深入，与海洋有关的研究领域从近浅海，逐渐向深远海的方向发展。与之相对应，作为水声技术中的重要设备，换能器也产生了多样的应用需求。其中，采用溢流设计的水声换能器因其在低频、大功率、深水工作性能等方面的优良特性，成为了换能器研究的热点。在溢流式换能器结构中，一般不存在空气背衬部分，换能器内外部实现静水压力平衡，故不需要压力平衡装置即有很好的深水工作能力[1-3]。许多设计中，换能器的内部充水之后形成Helmholtz腔体，由于腔体的体积模量远小于一般材料的杨氏模量，此时换能器有很好的低频发射能力[4]。其中一些溢流式换能器设计中利用换能器自身的谐振模态以及充水液腔谐振的模态相互耦合，形成多模态发射，拓展了换能器的工作带宽[5]。纵向换能器是一种典型的大功率发射换能器结构形式，双端纵向换能器(Janus)用于激发液腔共振的低频换能器，主要有Janus-Hammer Bell[6]和Janus-Helmholtz[7]两种形式，前者由双端纵向换能器驱动居中布置的、内径明显大于辐射头直径的单体圆环，后者由双端纵向换能器驱动分置于两端的、内径略大于辐射头直径的圆筒和双活塞背侧组成的液腔。本文在Janus-Helmholtz换能器基础上，结合Janus-Hammer Bell的设计思想，设计一种复合共鸣腔结构，通过多模态耦合工作原理，即利用一个可以双面辐射的Janus振子作为驱动，激发内部的液腔谐振与外部的圆环谐振，实现多模态发射，从而达到宽带工作的目的。本文首先介绍了换能器的基本结构与工作原理。之后使用有限元方法，仿真计算了Janus驱动振子的模态以及换能器在水中的发射电压响应，并对换能器的外接圆环部分进行了结构优化，分析了不同直径与高度的圆环对换能器发射电压响应的影响。最后根据优化结果设计制作了换能器的试验样机，通过实验，测试和验证了其宽频带工作特性。

1 复合共鸣腔Janus宽带换能器结构与谐振特性分析

复合共鸣腔Janus宽带换能器的结构如图1所示。换能器整体采用溢流设计，不存在空气背衬，可抵抗较大的静水压力，适于深水工作。其驱动部分为一个可双面辐射的Janus换能器，有源材料采用穿孔PZT-4压电陶瓷片，通过预应力螺杆将压电陶瓷晶堆、两端辐射头与中间质量紧固为一个整体。

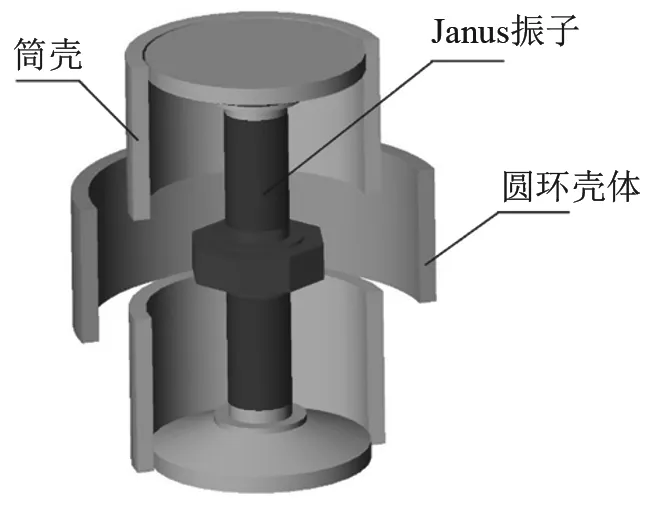
图1 复合共鸣腔Janus宽带换能器结构示意图Fig.1 Schematic diagram of Janus transducer with composite cavities

在Janus换能器两端辐射头之间加装了两个硬铝材料筒壳，中部开口形成溢流腔体，内部充水构成 Helmholtz液腔。换能器工作时，液腔谐振由Janus换能器辐射头的背板激发。一方面利用腔体较低的体积模量，增加低频模态；同时，也减弱了Janus换能器辐射头前后盖板之间的偶极子效应，提高了发射效率，这是Janus-Helmholtz换能器的基本工作模式，国内外许多学者对其基本工作特性进行了深入细致的研究[8-10]。本文的重点在于组成复合共鸣腔的外圆环设计。

在 Janus-Helmholtz换能器筒壳开口处引入一个弹性圆环壳体。为了使引入的圆环壳体对Janus-Helmholtz换能器的谐振特性影响较小，在高频端再形成一个圆环谐振模态，应使圆环的内径明显大于筒壳的外径、同时圆环的高度略大于筒壳开口的宽度。换能器中的Janus振子工作时，激发换能器周围介质做规律性的压缩与扩张，在合适的频率范围内，会激发圆环的弹性谐振。圆环的谐振频率为

式中：r为圆环内径；M为圆环自身质量；Ma为同振质量；c为水中声速。

在本文提出的换能器结构中，双端纵振动Janus换能器活塞背板激发内筒壳中水介质，再通过圆环内水介质振动激发外圆环谐振。故此时圆环工作时的同振质量近似为图1中复合腔内全部水介质的质量。忽略两活塞之间驱动件及结构件的体积，全部考虑成水介质进行估算，此时同振质量的表达式为

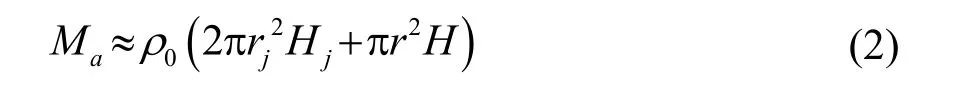
式中：H为圆环高度；内筒壳高为Hj；Janus换能器辐射头半径为rj；ρ0为水介质密度。将式(2)代入式(1)中，设t为圆环厚度，ρ为圆环材料的密度，可得本换能器中被动圆环的受激振动谐振频率为

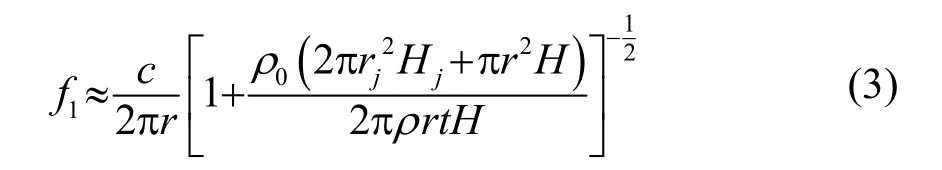
通过调整圆环壳体的结构参数，使得壳体在适当频率下的弹性谐振得到有效激发，从而使换能器宽频带发射响应中增添新的谐振成分、拓宽工作频带，而且由于多极子效应的存在，对换能器整体的声辐射也会产生影响，需要兼顾各个频率处的换能器发射能力，实现宽带工作特性。

2 换能器的有限元建模与分析

为了能够定量分析换能器的谐振频率、发射响应等电声特性，借助有限元方法是很好的选择。首先对换能器的Janus驱动振子建模，此部分主要是通过模态分析来研究其谐振频率、振动模态等特性。因振子本身具有良好的轴对称特性，可利用有限元分析中的轴对称模型与边界对称条件建立驱动振子的1/2轴对称二维模型，从而大大降低建模难度与计算时间。

驱动振子的有源材料为厚度极化的PZT-4穿孔压电陶瓷片，材料参数包括介电常数、压电常数、弹性常数和材料密度；前辐射头、预应力螺栓使用钛合金材料，中间质量块采用不锈钢材料，材料参数包括杨氏模量、泊松比和材料密度。整个 Janus振子建模的尺度为Φ178 mm×400 mm。

建模与模态分析结果如图2所示，主要利用的是Janus振子的一阶纵振模态，此模态对应的频率为2 664 Hz。虽然由于振子纵振模态与其他模态之间的耦合，振子的一阶纵振模态对应的谐振频率并不是换能器工作时相应的谐振频率，但作为换能器的驱动部分，其对换能器最后的工作频率范围起到至关重要的作用。同时，通过模态分析可得出振子的节线位于中间质量块处，这也为将来壳体的安装提供了参考。

换能器整体建模仍采用轴对称模型，只对换能器的上半部分建模，在模型的下边界添加对称边界条件。在Janus振子模型的基础上，增加筒壳与圆环壳两个部分。换能器筒壳采用硬铝材料，内径相较振子辐射头稍大，壳体厚度为20 mm，包覆于振子两侧辐射头的背侧。圆环采用铝材料，其结构参数分别为 r =145 mm，ρ =2 700 kg·m-3，H =120 mm，t =15 mm，c =5 090 m·s-1，ρ0=1 000 kg·m-3。

复合共鸣腔Janus换能器与相同尺度的Janus-Helmholtz换能器的发射电压响应有限元仿真结果对比如图3所示。可见在复合共鸣腔Janus换能器自身三个工作模态共同作用下，发射电压响应在1 300、2 300、2 900 Hz处出现了三个响应峰值，其大小分别为138、142、140 dB。其中，前两个谐振频率的激发近似于 Janus-Helmholtz换能器，与Janus-Helmholtz换能器相比，由于其额外的圆环模态，在较高频处产生了额外的谐振频率，发射电压响应在此处得到提升，拓宽了换能器工作频带的上限。

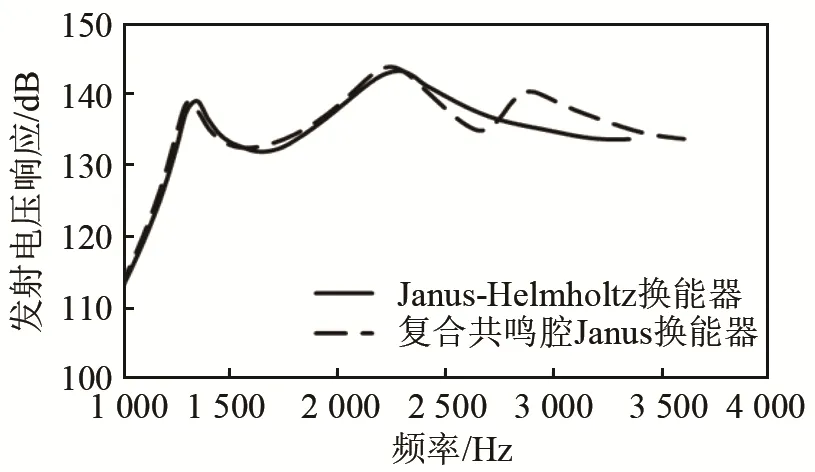
图3 复合共鸣腔Janus宽带换能器发射电压响应Fig.3 Transmitting voltage response of Janus transducer with composite cavities

利用换能器的水中建模，分析得出圆环参数对换能器发射性能的影响，从而对换能器进行优化设计。分析的结构参数主要是圆环壳体的高度H与半径r，分析结果如图4、5所示。

图4 不同圆环高度H的发射电压响应Fig.4 Transmitting voltage responses for different ring height H

图5 不同圆环半径r的发射电压响应Fig.5 Transmitting voltage responses for different ring radius r

可见圆环的引入增加了第三个谐振频率，该谐振频率与圆环的结构参数直接相关，同时圆环的结构参数对换能器第二谐振频率也产生了影响。随着圆环高度H的增加，第三谐振频率降低、响应有所提高，第二谐振频率处响应略有降低。改变圆环半径r对第二、第三谐振频率间的低谷有很明显的影响，随着r增加其低谷也更加明显。

图6、7分别为改变r、H后有限元仿真得到的第三谐振频率与利用式(3)得出圆环谐振频率的对比。

由图 6、7可知，谐振频率的计算结果与有限元分析的仿真结果有很好的一致性。

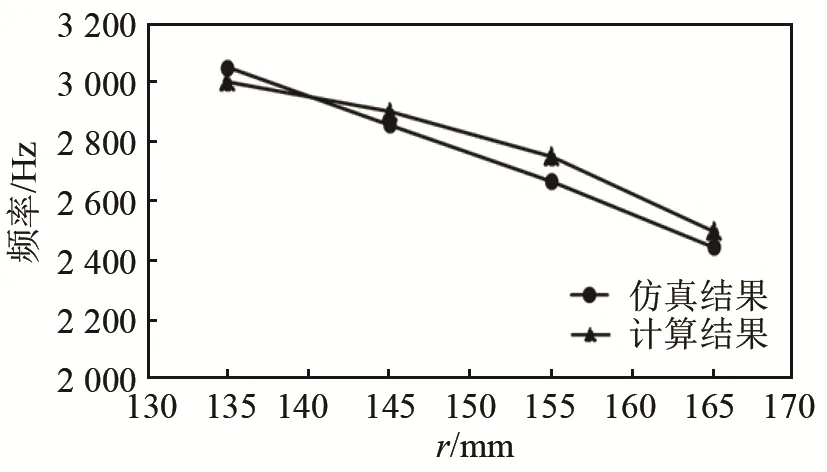
图6 圆环半径r改变时有限元仿真得到的第三谐振频率和式(3)计算的圆环谐振频率对比Fig.6 Comparison between the third resonant frequency obtained by finite element simulation and the ring resonant frequency calculated by Formula (3) when the ring radius r changes

图7 圆环高度H改变时有限元仿真得到的第三谐振频率和式(3)计算的圆环谐振频率对比Fig.7 Comparison between the third resonant frequency obtained by finite element simulation and the ring resonant frequency calculated by Formula (3) when the ring height H changes

3 换能器实验样机制作与实验验证

经过大量的仿真优化计算，最终确定了复合共鸣腔 Janus宽带换能器样机的尺寸为 Φ320 mm×400 mm。实验测试了这款换能器样机的发射性能，测试的主要参数是发射电压响应与谐振频率处的最大声源级，其中发射电压响应实测曲线如图8所示。由图8可见，实测发射电压响应与图3中计算的发射电压响应基本吻合，其中谐振频率略向低频偏移。

图8 换能器样机发射电压响应测试曲线Fig.8 Transmitting voltage response of prototype transducer

对换能器样机谐振点处的最大声源级进行了测试。在第一谐振频率1 250 Hz处，最大声源级可达200 dB，此时相应的发射电压响应为138 dB；在第二谐振频率 2 250 Hz处，最大声源级可达204 dB，此时的等效发射电压响应为142 dB；在第三谐振频率2 850 Hz处，最大声源级可达201 dB，此时相应的发射电压响应为139 dB。

由最大声源级的测试结果可知，换能器样机不仅可实现大功率发射，同时保持了很好的线性度。

4 结 论

总结全文，有以下结论：

(1) 本文在Janus-Helmholtz换能器基础上，结合Janus-Hammer Bell的设计思想，设计一种复合共鸣腔结构，根据多模态耦合工作原理，研制了一款复合共鸣腔Janus宽带换能器。

(2) 给出了复合共鸣腔条件下圆环结构的谐振频率计算公式，通过与有限元分析结果对比，证明了该公式对换能器谐振频率计算的有效性。

(3) 利用有限元方法分析了换能器的工作特性。在对圆环结构参数进行优化的基础上，设计研制了实验样机，实验结果表明，换能器性能与设计性能基本相符，可在设计的频带内实现宽带大功率发射。

(4) 在换能器各个谐振频率之间，仍存在发射电压响应较低的不足，进一步研究中需从换能器整体结构入手进行全面优化，重点改善发射电压响应的平坦度和低频发射的能力。