波纹管内部脱浆状态的超声检测方法

朱耀东，韩庆邦，林泽宙，尹琳丽

(河海大学物联网工程学院，江苏常州213022)

关键字：变分模态分解(VMD)；多尺度样本熵；蚁群神经网络

0 引 言

混凝土结构的波纹管作为工程建筑上不可或缺的材料被广泛运用于实际生活中。但是，在制作、施工和保养过程中的不当会导致波纹管内部存在缺陷和空洞等现象。为了减小这些因素带来的风险，利用无损检测来对波纹管内部压浆质量进行测试成为了当今热门的检测方法。其中超声法在工程建筑方面表现出良好的鲁棒特性，利用该方法检测混凝土内部缺陷，对被检测对象不仅不会造成损伤，而且还具有很好的检测效果。

由于混凝土包裹着的波纹管内部的复杂特性，传统检测方法通过回波的幅值或频谱来对混凝土缺陷进行判定比较依赖操作者的主观经验，难以实现规范化[1]。所以有效处理这种非平稳非线性信号，是解决该类问题的关键。经验模态分解(Empirical Mode Decomposition, EMD)在对非平稳非线性信号进行处理时，有明显的处理效果[2]。但是EMD方法在实际使用中容易产生模态混叠的问题。集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法克服了模态混叠，但由于添加了白噪声，并不能有效中和干扰，同时还增加了计算量，存在一定的局限[3]。Wang等[4]，Dragominetskiy等[5]提出用变分模态分解(Variational Mode Decomposition, VMD)自适应地将信号分解为一系列本征模态分量(Intrinsic Mode Function, IMF)，克服了上述模态混叠问题，还提高了计算效率。郑豪等[6]将EEMD与支持向量机(Support Vector Machine,SVM)相结合，根据IMF的能量分布来检测波纹管压浆质量，但只能对波纹管内部是否存在严重脱浆进行判断。成锦等[7]利用小波熵的熵值来判断波纹管压浆的密实度，得到了熵随缺陷大小的变化关系，但不同程度缺陷的小波熵值区分度不高。陈媛等[8]通过奇异熵对波纹管内部缺陷的横向尺寸进行分析，得到缺陷与奇异熵的单调关系，但无法直接从熵值判断是否存在缺陷。本文和上述方法都通过对复杂回波信号进行分析，来对波纹管进行检测。本文将回波信号经变分模态分解后得到的本征模态分量的样本熵进行多尺度化。变分模态分解相比于EEMD能更好地抑制模态混叠。多尺度样本熵相对于上述方法中使用的单一熵，将熵多尺度化能够得到更完备的信息。相比于上述方法，本文通过与神经网络相结合，来提高缺陷的识别能力。传统神经网络收敛较慢，对初值过于敏感。蚁群神经网络解决了收敛慢的问题，并且有较好的鲁棒特性。本文将VMD与蚁群神经网络相结合，不仅解决了频谱混叠、计算量大等问题，还加快了收敛速度，提高了分类模型的判断精度。结果表明，该方法能有效地判别波纹管内部的脱浆状态。

1 VMD和蚁群神经网络

1.1 VMD和多尺度样本熵理论

相对于传统递归形式分解的EMD方法，VMD将测得的信号以非递归的形式进行分解。在 EMD分解的本征模态函数(IMF)的基础上，将信号以调幅调频的方式重新定义该函数，如式(1)所示：

将初始信号f假设为是一个由K个有限长带宽的本征模态函数IMF的分量ul组成。假设对应中心频率为φl，建立如下的约束变分模型为

本文采用近似熵类似的样本熵[9]，并将样本熵扩展到多个时间尺度的多尺度样本熵并作为特征提取的参数选择。样本熵作为在条件概率情况下的严格对数一般用Es表示，当N为一个有限值时，有如下估计：

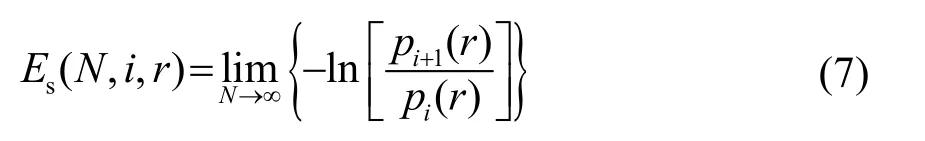
多尺度样本熵是将信号序列经过粗粒化后，计算对应不同粗粒序列对应的样本熵值，即：

式中，ℑ为时间尺度。相对于样本熵，多尺度样本熵摆脱了样本熵只能在单一尺度下衡量序列的局限性，可以得到对应不同尺度因子所产生的不同模式序列的可能性[10]。

1.2 蚁群神经网络

蚁群算法是一种利用动物从栖息地到食物点的过程中如何确定最佳路线的一种随机的搜索算法。基本原理就是利用蚂蚁在觅食行走的过程中，会在途经的路线上留下一种被称为是信息素的物质，在信息素扩散的范围内其他孤立的蚂蚁会倾向于沿着信息素含量较高的地方移动，通过这种方法来寻得数据分析过程中最佳路径的机制[11]。

将该算法与人工神经网络相结合。人工神经网络由输入、输出和隐藏层构成。由神经元的“突触”连接着输入和输出。该网络的结构如图1所示。图1中，a1, a2,…ap是神经网络的输入，bh1, bh2…,bhp是该网络对应的神经元，经过激活函数得到输出。

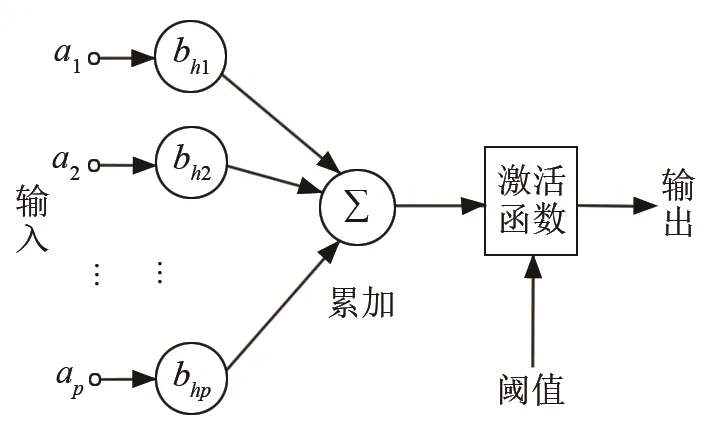
图1 神经网络框图Fig.1 Block diagram of neural network

2 仿真分析

2.1 仿真模型及信号特征

工程中运用的混凝土结构多是由混凝土为主材料，里面加入波纹管、钢绞线、水泥等形成的一种复合结构。由于在压浆的过程中管道渗入了空气，导致管道内出现了大小不一的空腔。本文基于COMSOL Multiphysics仿真软件[12]对模型进行仿真，模型的尺寸：长为150 cm，宽为50 cm。波纹管内径长为84 mm，管壁厚度为 3 mm，中心钢绞线的直径为10 mm。将模型分为5个部分，其中S1为无脱浆状态，S2～S5为相同纵向尺寸下、不同程度的横向脱浆。波纹管仿真模型如图2所示。

图2 波纹管仿真模型Fig.2 Simulation model of corrugated pipe

通过保持纵向缺陷一致的情况下，来比较不同尺寸横向缺陷对经过变分模态分解后的多尺度样本熵的影响。仿真缺陷尺寸对应如表1所示。

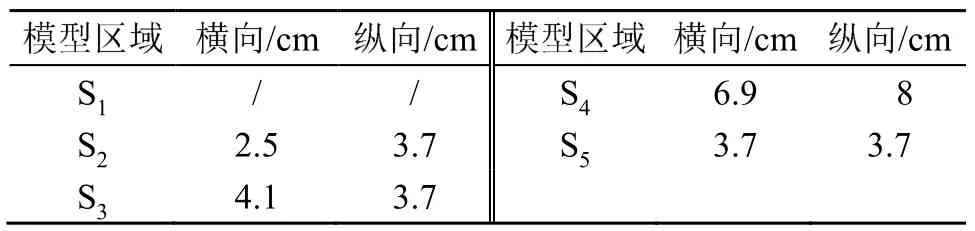
表1 仿真模型对应缺陷尺寸Table 1 Defect sizes of simulation model

在仿真过程中采用宽度是 20 mm的激励源作为发射端口，以自发自收的形式来对回波信号的信息进行提取。该激励信号是经过汉宁窗函数调制的单脉冲信号，表达式为

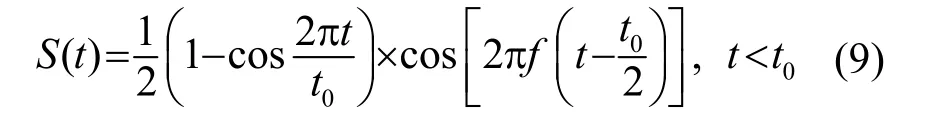
式中：f为中心频率，取值为200 kHz；t0=1 0µs 。

针对S1～S5不同缺陷对应的回波信号，对各回波信号进行分解。为了节省篇幅，本文只列出两个最具代表性的缺陷回波信号：没有缺陷的S1和脱浆程度最严重的S5。其中，无缺陷的信号和脱浆最严重的缺陷信号如图3和图4所示。

图3 波纹管内无脱浆缺陷(S1)的回波信号时域图Fig.3 Time domain diagram of the echo signal inside corrugated pipe with no desizing defect (S1)

图4 波纹管内有严重脱浆的缺陷(S5)回波信号时域图Fig.4 The time domain diagram of the echo signal inside corrugated pipe with severe desizing defect (S5)

2.2 信号处理及分析

由于本文的特征选取是多尺度样本熵，而熵可以反映序列的复杂度，并且样本熵对于数据长度不会存在依赖性，所以对接收到的回波信号整体进行VMD分解。取惩罚因子α= 2 000。根据峭度原理取选出对应的分解层数K=5。得到了对应的无缺陷(S1)和脱浆程度最严重(S5)两种类型的回波信号的变分模态分解图，如图5和6所示。

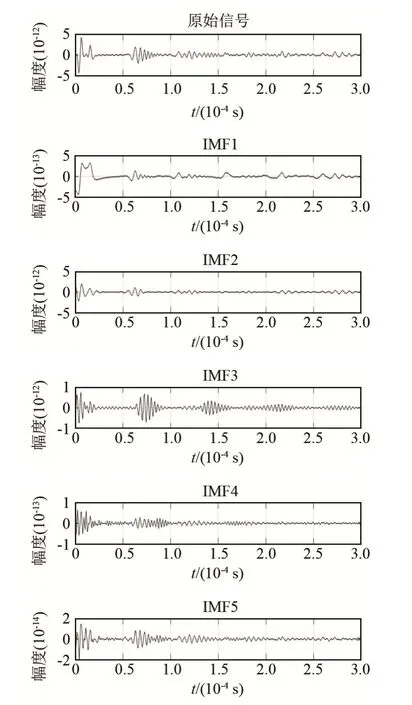
图5 无脱浆状态的回波信号S1的变分模态分解图Fig.5 VMD diagrams of the echo signal S1 in no desizing state

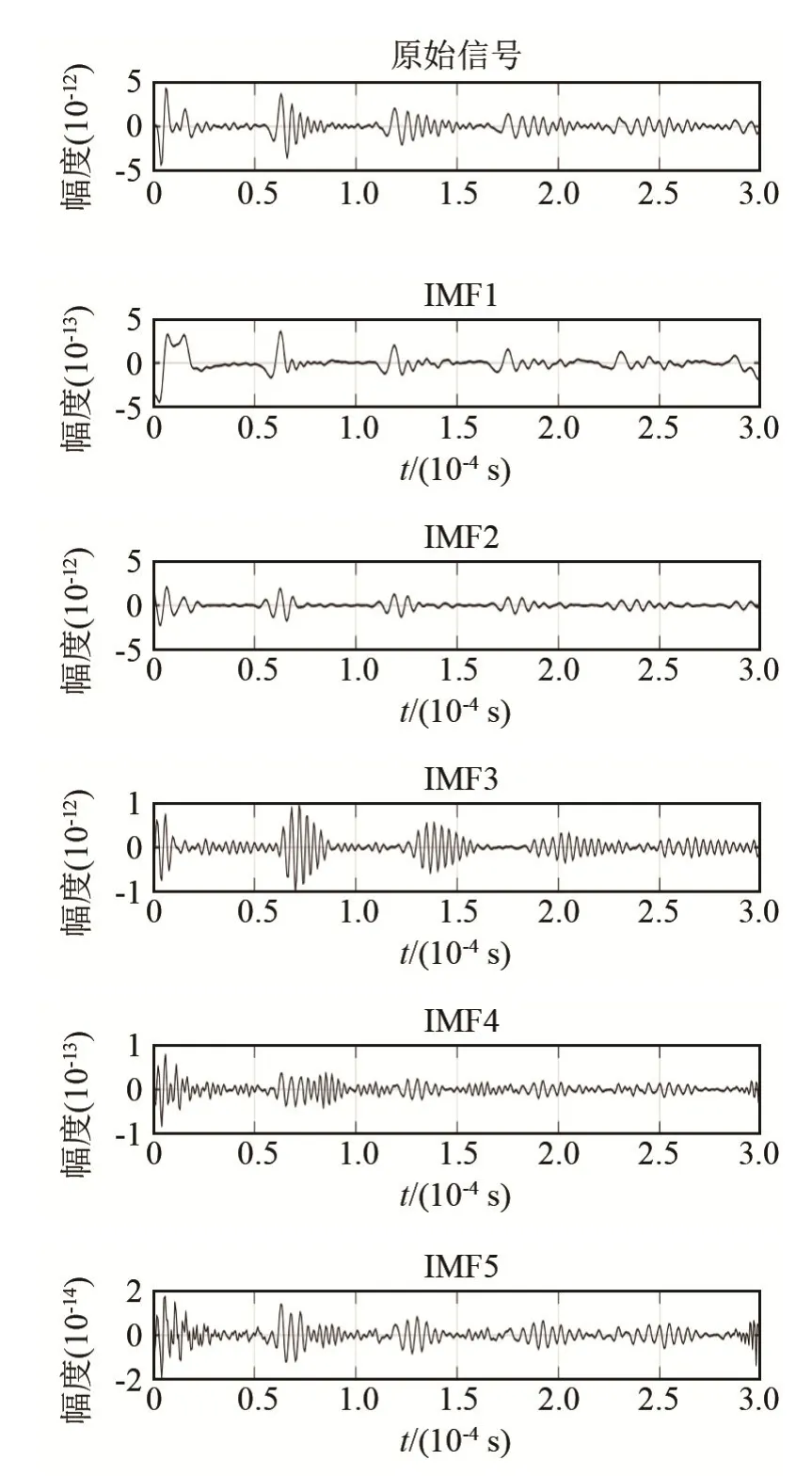
图6 严重脱浆状态的回波信号S5的变分模态分解图Fig.6 VMD diagrams of the echo signal S5 in severe desizing state

将不同脱浆程度模型分为三类。模型区域 S1作为无损伤A，将模型区域损伤最严重的S5看作损伤程度C，将模型区域损伤程度只占约C一半的S3作为损伤程度B，根据对应信号产生的5个不同的模态分量，分别计算多尺度样本熵值并进行求和。得到对应的多尺度样本熵变化曲线，如图7所示。

图7 仿真的多尺度样本熵曲线Fig.7 Simulated multi-scale entropy curves

并将划分的三种程度(A,B,C)对应区域的探头移动±20 mm(一个探头直径)的范围区间得到 40个样本，再向样本中添加高斯随机噪声，对样本进行扩充，扩充至300个样本数进行训练。

将无损伤A的理想输出设为(1,0,0)，将损伤最严重的C的理想输出设为(0,0,1)，将损伤程度约为损伤C一半的B的理想输出设为(0,1,0)。将经过训练后的识别模型用来检测上述仿真模型。

以多尺度样本熵作为特征参数，并对神经网络进行训练，步骤如下：

(1) 对各参数进行初始化。令时间t=0，循环次数Mc也进行初始化，默认设置最大循环次数是Mcmax。

(2) 开始模拟蚁群外出觅食。用m只蚂蚁对q个地点路线进行规划：在t时刻，蚂蚁k在x地点转移到y地点的概率 Pxy,k(t)为

当m只蚂蚁都在某一路径收敛时，停止迭代。建立蚁群神经网络流程图如图8所示。实际神经网络的输出向量如表2所示。可以发现S2的输出向量接近B类，S4的输出向量接近C类。所以进行如下分类：S1内缺陷为A类，S2, S3区域内缺陷为B类，S4, S5区域内缺陷为C类。

表2 仿真模型不同缺陷的神经网络输出Table 2 The neural network outputs of different defects in the simulation model

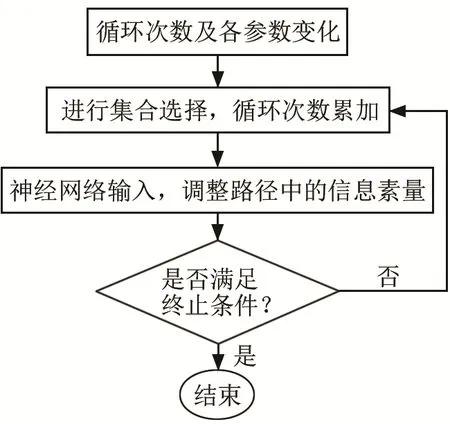
图8 蚁群神经网络流程图Fig.8 Flow chart of ant colony neural network

从蚁群神经网络预测的分类结果可以看出，利用该方法可以在纵向缺陷不变的情况下，定性得到不同横向缺陷导致的损伤程度。

3 实验分析

针对仿真中得到的结果，本文对实际的波纹管进行了检测，浇筑的波纹管模型如图9所示。

图9 实验浇筑模型Fig.9 Experimental casting model

上述浇筑模型的结构尺寸为 1 000 cm×50 cm×100 cm(长×宽×高)。其中波纹管内径为 69 mm，管壁壁厚3 mm。在波纹管内部预设了纵向尺寸一致，横向尺寸分别0、10、30、48、57、81、90 mm的多处空腔，并标记为①～⑦，如图10所示。

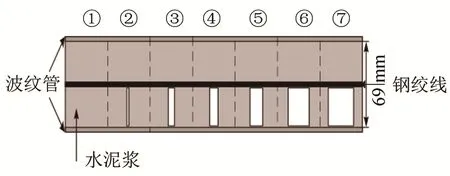
图10 实验模型结构图Fig.10 Structure diagram of experimental model

本次实验采用了单脉冲激励，该激励源的工作频率是200 kHz，以1 MHz作为它的采样频率。仍然以单发单收的形式，保持发射接收间距固定，通过移动发射位置，在有、无缺陷区域获取回波信号。

将所有实测信号代入VDM进行分解。实验中也只列出最具有代表性特征的两个信号(无损伤和损伤程度最严重)如图11和12所示。将缺陷分为无缺陷A，受损B和受损C三类。A代表预设横向尺寸为0，C代表最严重的损伤尺寸90 mm，B代表损伤约占最严重损伤程度一半的损失尺寸48 mm。按照仿真处理方式，得到图13所述处理后的三条多尺度样本熵的曲线。

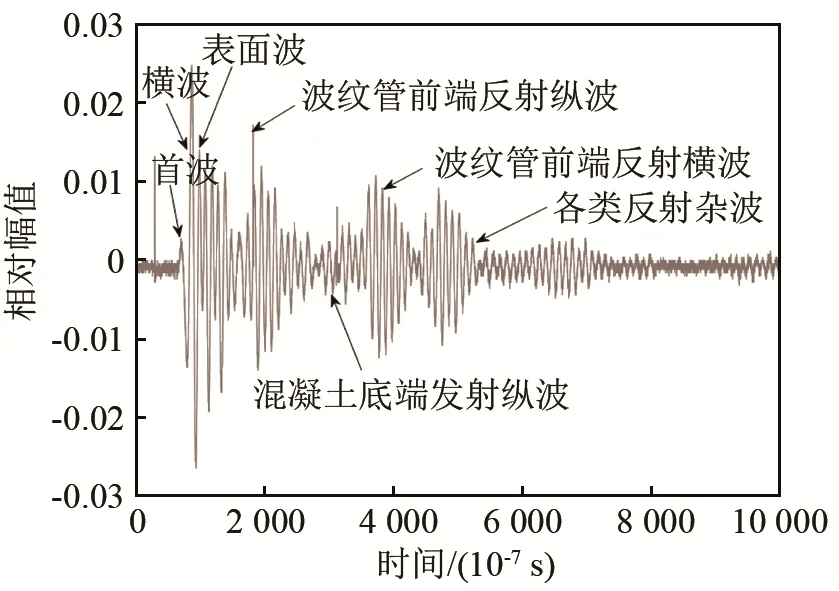
图11 实测回波信号(无缺陷)Fig.11 The measured echo signal with no-defect

图12 实测回波信号(缺陷横向尺寸为90 mm)Fig.12 The measured echo signal with 90 mm transverse defect

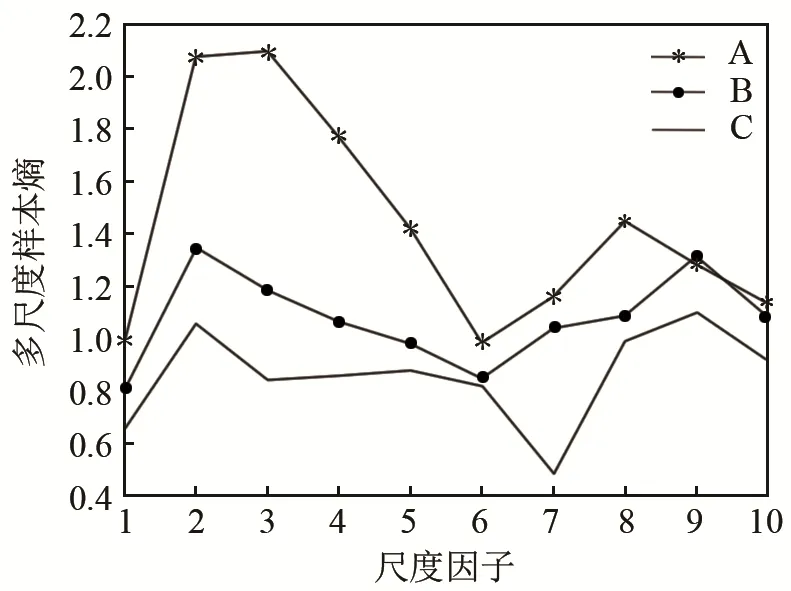
图13 实测信号多尺度样本熵曲线Fig.13 The measured multi-scale entropy curves

可以发现对于实测信号多尺度样本熵的提取过程中，划分的三类程度仍有较为明显的区分度。同时，从 A，B，C三类缺陷对应区域中心位置 ±20 mm(一个探头直径)范围内测得40组数据。由于预设的实验模型中，相同尺寸的缺陷在浇筑的模型中都分别有 10个这样的缺陷分布于模型的不同位置，且位置已知。所以可以得到400组数据，从中任取300组作为训练集进行训练。并根据训练生成的识别模型对实验浇筑的模型进行测试。将无损伤A的神经网络输出设置为(1,0,0)，最严重损伤C的神经网络输出设置为(0,0,1)，损伤约为最严重损伤程度C一半的损伤为B，其理想神经网络输出设为(0,1,0)。模型纵向尺寸相同，对应不同的横向尺寸为：0、10、30、48、57、81、90 mm 作为测试集输入到识别模型中得到表3所示输出结果。根据输出结果，通过三个输出最大权重进行分类，分类见表3。

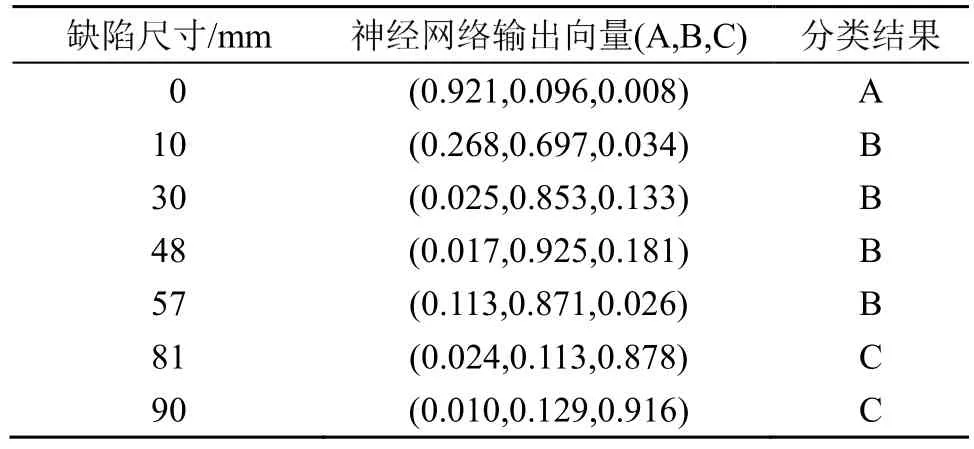
表3 实验模型中不同缺陷的神经网络输出及分类结果Table 3 The neural network outputs and classification results of different defects in the experimental model

实验结果表明，利用变分模态分解与蚁群神经网络相结合的方法能对波纹管内部压浆情况做出初步的判别。

4 结 论

针对超声回波难以有效获取波纹管内部脱浆情况，提出了一种基于变分模态分解与蚁群神经网络相结合的无损检测方法。同时，VMD作为一种非递归的自适应分解方法，能较好地处理回波信号问题。利用多尺度样本熵作为特征参数代入蚁群神经网络，能够较直观地反映波纹管内部不同横向尺寸缺陷导致的脱浆问题。但是，该方法的局限在于对小尺寸缺陷的判别结果还需要更精确的细分以及尺寸的定量分析，这也是下一步需要完善的工作。