夹层输流管道弹性波频散特征分析
2021-05-10陈德锦罗杨阳邹律龙
陈德锦,严 谨,罗杨阳,邹律龙
(广东海洋大学,广东湛江524088)
0 引 言
输流管道作为传递动量流和能量流的主要工具,被广泛应用于机械、船舶、工业等领域。由内外钢管与中间层填充轻质材料组成的夹层管道由于自身减振降噪隔热保温等优良性能,常被用作输流管道。目前对夹层输流管道的研究主要集中在热学性能与强度的研究,对夹层输流管道声模态的研究较少。声学性能分析是管道故障声检测的核心技术,所以研究夹层管道振动及内部声波导模式是非常必要的。
目前基于声固耦合理论研究管道响应的主要方法包括:解析法、实验法和数值分析法[1],其中采用数值分析法的研究居多。解析法一般把输流管道简化为梁模型或圆柱壳模型。此方法物理意义清晰、明确,便于揭示本质。郭文杰等[2]利用半解析法对部分浸没圆柱壳结构实现了声固耦合系统的建模与求解,并讨论了部分浸没圆柱壳体的前四阶耦合周向波型,但是,此方法使用条件苛刻,对于复杂结构,解析法的求解十分困难。Maze等[3]通过实验法得出了薄壁壳声模态模型单边受载和不受载时管壁弹性波的频散曲线存在“排斥现象”。声学实验易受外界环境的影响,测试结果容易出现误差。基于声固耦合的管道结构与声模态数值研究,蒋謇等[4]通过数值计算得到了孔隙介质包裹充液管道的纵向导波频散曲线,分析了孔隙介质参数和壁厚对频散曲线的影响。张术臣等[5]通过数值分析法计算了圆管的纵向导波和周向 Lamb波的频散曲线,得出了这两种模态的波动特性。刘泽等[6]通过数值分析软件求出了黏弹性管道纵向导波频散线和衰减曲线,得出了波在黏弹性管中的传播特性。数值分析便于物理模型的构建及边界条件的假设。以上对于管道模态的研究主要采用材料属性单一的管道,涉及夹层材料管道的声模态研究较少。
本文运用声固耦合理论,对无限长夹层输流管道进行数值模拟并且构建弹性管壁与流体中弹性波的波数解析式。比较夹层管道内部为空气和水两种流体情况下的频散曲线,计算结果给出了无限长夹层管道波数与频率之间的关系以及管壁的变形情况,描述了波导的动态特性以及特征模态。在输流管道中,波不仅能在流体域中传播,也能在管壁中传播,频散曲线显示了各种波的特定传播性质。
1 管道弹性波理论
1.1 管中导波模态
管道中导波具有频散与多模态特征[7],输流管道模型一般情况下被构建为梁模型或壳模型。其中梁模型分为欧拉伯努利梁和铁木辛柯梁,欧拉梁模型忽略管道剪切效应,对于管壁较厚的复合材料的管道,忽略剪切变形是不妥的,铁木辛柯梁模型更加适合对夹层管道的分析。因此,本文对夹层管道采用铁木辛柯梁模型进行构建,依据管道的轴线方向与波的运动方向之间的相对位置,可将固体弹性波分为剪切波、纵向波以及弯曲波[8],声学域中模态分为周向模态与径向模态[9]。
1.2 管壁波数
在 xy平面内受横向荷载作用引起横向振动的铁木辛柯梁模型如图 1所示。运动方程如式(1)所示[10]:

图1 铁木辛柯理论模型Fig.1 Timoshenko's theoretical model

式(1)中:E为弹性模量;G为剪切模量;µ为截面形状因数;ρ为梁材料的密度;A为梁截面面积;I为梁截面对中性轴的惯性矩。由于管道为圆截面,所以根据剪切所计算的应变能理论,µ取0.9。
假设所受外力为 0,即q=0,将方程基本解y= B ei(ωt-kx)以及波数k=ω/c(B为波幅,ω为角频率,c为波速),代入方程(1)得:
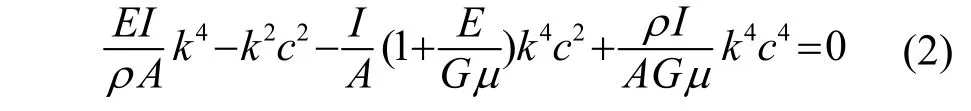
为了简化方程,令:

方程(2)可化简为

令ω= 2 π f ,其中f为频率,可得管道铁木辛柯梁模型弯曲波数为
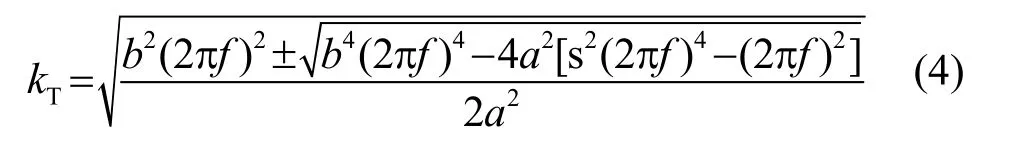
管道纵向振动模型如图2所示,其中u表示x处横截面上一点的纵向位移,S表示x处横截面上的轴向应力合力,A为横截面面积,ρ为材料的质量密度,当管道纵向振动时,每一分段上的轴向力根据达朗贝尔(D'Alembert)定理[11]可得:
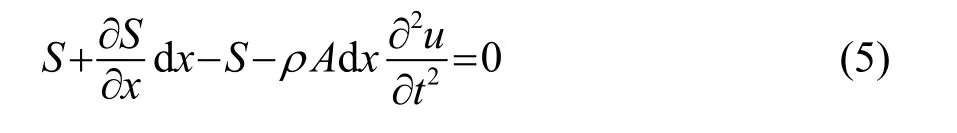

图2 管道纵向振动模型Fig.2 Longitudinal vibration model of pipeline

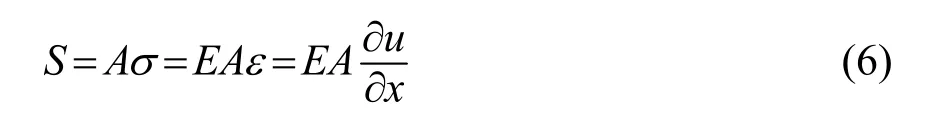
根据波数与频率的关系,将式(6)代入式(5),得管道铁木辛柯梁模型纵向波数为


图3 管道剪切振动模型Fig.3 Shear vibration model of pipeline

列出动力学方程[12]得:

将ω= 2 π f 与式(8)代入式(9),可得管道铁木辛柯梁模型切向波数为

最终得到夹层管道弯曲波数解析方程(4),纵向波数解析方程(7),剪切波数解析方程(10)。
1.3 管道流体域波数
夹层输流管道的管壁作为刚性壁面,以刚性壁面圆管波导来讨论管内流体域中简正波的传播特性,即管内声模态传播特性。
首先假设波导中存在(n,m)阶简正波,则在柱坐标系下该简正波函数为



表1 方程dJn(x)/dx=0的第m个根βnm的值Table 1 Value of the m-th root (βnm) of the equation dJn(x)/dx=0
由于管壁为刚性壁面,所以,当r= a时,径向波速vr= 0 ,即

式中:kr指的是径向模态,根据柱贝塞尔函数Jn(x)的递推关系得出:

利用表1的值,可以根据式(13)解出无限长夹层管道简正波的每一阶波数方程。


式中:m≥0,n≥0,m、n均为整数。
2 管道声固耦合理论
声固耦合属于多物理场问题,流体域与固体域通过声固耦合边界实现数据交换,在边界处流体域声波会在固体域中产生声压载荷,固体域的振动会对流体域产生法向加速度。
2.1 管道模型简化假设
声固耦合的数学模型需要满足三个基本物理方程,即质量守恒方程、动量守恒方程和能量守恒方程[13]。
模型假定:
(1) 声学域为理想流体,声波在管道中传播无损耗且不存在粘滞性;
(2) 在声波传播过程中,所有的热力学是等熵过程;
(3) 管道中的传播都是小振幅振动,声学参量忽略二阶以上微量;
(4) 只考虑与管束轴线相垂直的平面内的声场情况;
(5) 忽略管道内流体流动时所引起的噪声;
(6) 没有声扰动时,管道在宏观上是均匀、静止的。
满足以上条件可将管道模型简化为二维模型,即将三维管道模型简化无限长管道模型。
2.2 声固耦合控制方程及边界
描述空气中声波传播的方程[14]可从流体流动的控制方程推演而来。无损介质中压力波的波动方程为

其中:Qm为单极子域源,是一个质量源,单位为s-2。qd为偶极域源,是一个力源,单位为N·m-3,p为声压,ρ为材料密度,c为波速,由于本模型中不受外源影响,所以该两域源数值为0。
声固耦合边界条件为

其中:n为耦合面法向量;pt为总声压;utt为结构加速度;FA为结构一侧所受单位面积力。
在声固耦合中,结构体的控制方程是根据牛顿第二定律[15]决定的,结构控制方程可表达为

其中:方程右边两项∇⋅s、FV分别为面载荷与体载荷。
3 数值模型构建
本文使用COMSOL Multiphysics多物理场仿真软件进行数值分析。以二维平面构建无限长夹层管道模型,内部横截面呈圆形。在模型中,夹层管道内径为 0.054 m,外径为 0.07 m,管壁内外为结构钢,内层厚度为0.003 m,外层厚度为0.002 m,夹层材料为聚丙烯[16],厚度为 0.003 m,分别计算管道充水和充气两种情况。所使用的材料参数如表 2所示,无限长夹层输流管道模型如图4所示,声固耦合边界为半径最小闭合圆曲线。

表2 材料参数Table 2 Material parameters

图4 无限长夹层输流管道模型Fig.4 Model of unlimited length sandwich pipe conveying fluid
声学域网格采用自由三角形网格划分,结构域网格采用映射分布划分,分布类型为固定单元数,单元数取 5,声学域需严格遵循网格最大单元尺寸小于1/5波长即每个波长涵盖5个以上网格单元的原则,这样声学分析时才能准确。对建立的几何模型进行模式分析,求解模式数设为20,给定模式分析频率f0=1 000 Hz,模式搜索基准值设为1. 1k0,参数化扫描频率范围为 10~12 000 Hz,间隔取100 Hz,其中。解析计算结果是将文中推导的波数公式编程嵌入至COMSOL Multiphysics中进行计算,x轴表示频率,y轴表示波数,以此完成频散曲线解析计算。通过求解分别得到了夹层输流管道内部充水和充气两种情况下的频率-波数频散曲线,以及内部声压与管壁形变云图。
4 计算分析
4.1 频散关系分析
本文计算了无限长夹层输流管道的三种频散关系,分别是内部声模态频散关系、管壁弹性模式频散关系以及耦合时的频散关系。由于在中低频条件下,所以本文求解流体域前8阶声模态面外波数(即轴向波数)解析解,阶次分别为:(0, 0)、(1, 0)、(2, 0)、(0, 1)、(3, 0)、(0, 2)、(0, 3)、(1,1)。夹层输流管道内部为空气时,不同弹性波模态的频散曲线如图5所示,夹层输流管道内部为水时,不同弹性波模态的频散曲线如图6所示。
夹层输流管道内部流体是空气时,从图5(a)可以看出,声模态解析计算结果与数值计算结果基本一致,在计算的前8阶模态中,(0, 2)和(0, 3)阶声模态不存在,说明此时扫描频率没有超过该阶次的截止频率,该阶次声模态无法在管道内传播。(0, 0)阶声模态是直通模式,因此该阶次不发生频散现象,其他存在的阶次都发生了频散现象。
夹层输流管道的管壁弹性模式在图5(b)中可以看出,管壁纵向模态和剪切模态的解析计算结果与数值计算结果基本吻合,由于梁模型弹性波频散特性,弯曲模态在4 000 Hz前吻合度较好,4 000 Hz后产生了偏差,偏差随着频率的增加而加大。在数值模型计算中可以看出,管壁模式中还有其他传播模态,例如由结构特征变化派生的环形模态,在声学探测中需尽量避免此模态的产生,因为该模态由模态叠加形成,会增加检测信号的复杂性。还有的模态特性在较高频处发生变化,弯曲模态转变为剪切、纵向模态。
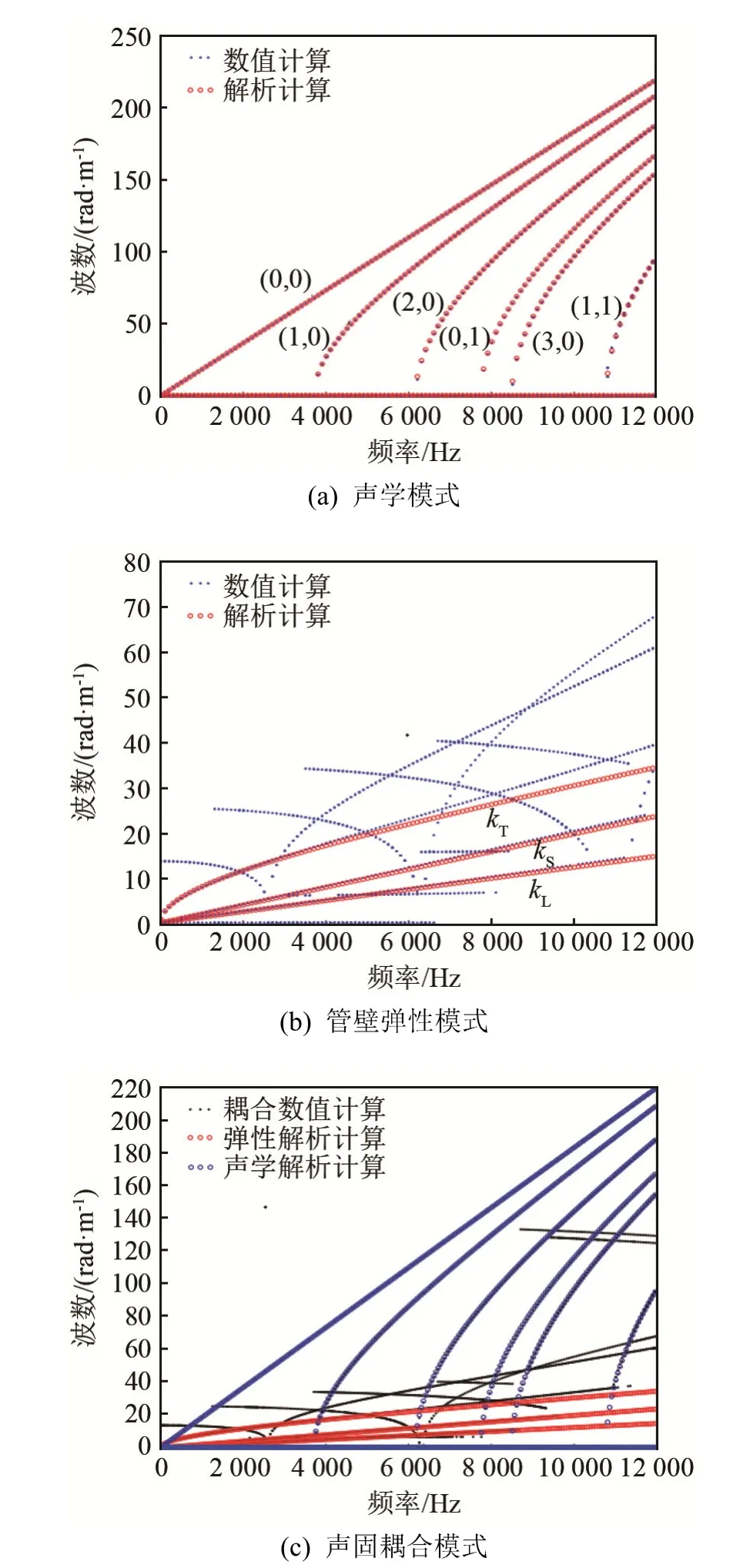
图5 充气夹层管道内不同弹性波模态的频散图Fig.5 Dispersion diagrams of different elastic wave modes in the gas-filled sandwich pipe
在声固耦合模式下频散曲线较为复杂,从图5(c)可以得出,夹层输流管道产生弹性波模态的总数大于两个单模式之和,这说明多出的模态是在耦合时产生的。所以针对多出的耦合模态,可利用有效数据来对耦合情况进行进一步分析。耦合时的声模态以及管壁弹性模态与非耦合情况下各单模式的计算结果基本吻合,说明构建的解析式适用于内部为空气时的夹层输流管道的频散特征分析。夹层输流管道内部流体是水时,从图6(a)可以看出,声模态解析计算结果与数值计算结果基本一致,但只存在“直通模式”即声波均匀、声压幅值分布一致的(0, 0)阶声模态。水中传播的声模态较少,不易发生频散现象,所以流体介质属性决定着管道内部的声模态特征。

图6 充水夹层管道内不同弹性波模态的频散图Fig.6 Dispersion diagrams of different elastic wave modes in the water-filled sandwich pipe
从图6(b)可以看出,管壁纵向模态和剪切模态的解析计算结果与数值计算结果基本吻合,在高频段有偏移但误差偏移量极小可忽略,弯曲模态在高频的偏移量较大。所以在高频段利用铁木辛柯梁模型对充水夹层管道的弯曲波数建立解析式不适用,在中低频段铁木辛柯梁模型波数解析式较适用。
从图6(c)可以看出,在耦合情况下,构建的声模态波数解析式在扫描频率为2 000 Hz之后与数值解产生了误差,并随着频率的增加而加大,管壁弹性波弯曲模态误差在此处也随着频率的增加而加大。在8 500 Hz处发生了“模态干涉”现象,即两个相邻模态出现了交叉点,此现象的产生是由于受到机械能转化的影响。
4.2 截止频率及模态分析
夹层输流管道截止频率可从构建的解析式中计算得出,管道内充水情况下,由频散曲线可以看出只存在直通模式,直通模式在任何频率下都可以产生,所以无须做截止频率计算。充气情况下管道在扫描频率范围内存在6种模态,阶次分别是(0, 0)、(1, 0)、(2, 0)、(0, 1)、(3, 0)、(1, 1),通过计算可得出,截止频率分别为0、3 810、6 210、7 810、8 510、10 810 Hz,与数值计算结果基本一致,绘制出的夹层输流管道模态图(见图 7)也与相应的波导截面上简正波幅值分布图[14]一一对应,每个截止频率对应一阶模态,再次验证了构建的解析式的准确性。从图7中可看出管壁变形情况与内部声压分布情况。

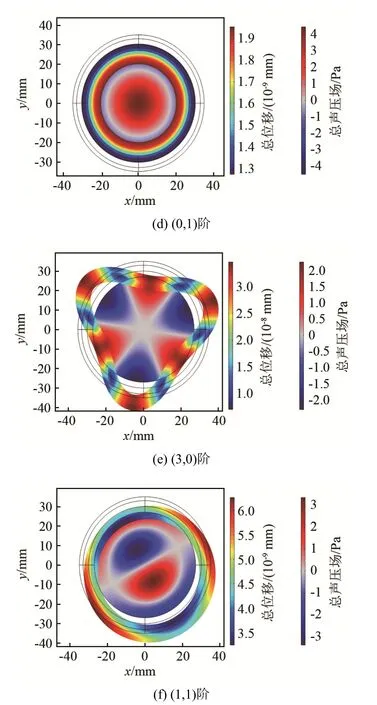
图7 充气夹层输流管道内不同弹性波的模态图Fig.7 Nephograms of different elastic wave modes in the gas-filled sandwich pipe
5 结 论
基于声固耦合理论,利用多物理场数值计算方法分别对充水和充气的无限长夹层输流管道进行弹性波频散特征分析,根据内部声学传播模式和铁木辛柯梁模型建立无限长夹层输流管道弹性波波数解析式,得出这些解析式所适用的频率范围。通过模式分析计算可得出:
(1) 管内充水时声学域只存在直通模式,管内充气时存在多阶声学模态,耦合状态时两者都存在“模态干涉”现象。
(2) 通过解析计算得出的管道截止频率与数值计算结果基本一致,并且绘制出各截止频率下的声波模态图,与对应的波导截面上简正波幅值分布图一致。
(3) 研究结果证明了所建立的铁木辛柯梁模型的波数解析式适用于充气夹层输流管道的频散特征分析,充水夹层输流管道的弯曲波数解析式在高频段不适用。
研究具有合理性和可行性,可为夹层管道声固耦合理论的运用提供一定的参考,为夹层管道故障的声检测提供一定的理论依据。
