基于钟差建模的水下定位时延修正算法

王雪琰，李记龙，黄敏燕，冯海泓

(1. 中国科学院声学研究所东海研究站，上海201815；2. 中国科学院大学，北京100049)

0 引 言

近年来，经济、科学和军事等方面在海洋领域的高速发展以及人类在海洋活动空间的不断拓展，对水下定位导航授时(Positioning Navigation and Timing, PNT)提出了越来越高的要求[1]。水下定位导航目前主要手段有惯性导航、地球物理场导航和水声导航定位[2]。水声定位应用广泛，灵活多变，有广阔的发展前景，是水下定位的主要手段。目前水声定位的方法主要有超短基线(Ultra-Short Baseline,USBL)定位系统、短基线(Shoot Baseline, SBL)定位系统和长基线(Long Baseline, LBL)定位系统。其中LBL的基线范围达几千米，基阵常常布放在海底或海面，目标处于基阵内。装有应答器或同步信标的基阵固定在海底时，通过测量时延可以获得每个应答器与目标的斜距。在应答器位置预先确定的条件下，根据球面交汇原理即可确定目标的位置。水下定位中存在各种误差因素。易昌华等[3]较全面地剖析了二次水声定位过程中GPS测量、坐标系转换、换能器安装、时延测量、声速计算中存在的误差，并给出了减小和消除各种误差的方法。对于声速误差，赵建虎等[4]认为削弱声速相关误差的有效途径是建立声速场模型，且声速对定位的影响与波束入射角密切相关。孙文洲等[5]分析了声速剖面对定位测距的影响，根据误差变化规律设计了对应的走航方式与差分算法。孙大军等[6]提出了一种通过遗传算法提取最优有效声速的方法，以修正非均匀声速带来的误差。关于GPS测定船姿态的误差影响，赵建虎等[7]提出了利用GPS相位测量技术对船姿态进行测定，提高了数据获取精度。

海洋大地控制网是由一系列布设在海洋领域的测量控制点构成的大地控制网，是国家测绘局布设的“2000国家大地控制网”的重要组成部分[8]。由陆上、海面、海底三方面的控制点组成，其中最主要的是海底控制点。建设完备、精确的海洋大地控制网是海洋测量、检测、定位、水下作业等海事活动的基础。但由于水下测量的局限性，水下控制网点的绝对位置标定难以精确实现。通常布放在海底的固定节点的位置无法直接准确得知，故需对沉底潜标通过水面观测收集一系列时延信息以对其进行精确标定。时延获取有应答与同步两种方式，在通过同步方式获取时延值时，水面设备与水下设备精准的时钟同步是获取精确时延的前提条件。由于水上GPS设备与水下设备存在固有钟差，在定位时延中增加了一个干扰参数，使得获取时延存在误差，进而导致标定误差。由此可见钟差也是影响定位精度的一个重要因素，故建立水下同步信标的时钟漂移模型是亟待解决的问题。

卫星钟差的建模与预报已有许多学者进行了大量的研究，旨在修正卫星导航系统与地面设备系统之间的钟差[9]。目前主要的预报方法有多项式模型、灰色模型、卡尔曼(Kalman)滤波模型、各种神经网络模型、时间序列模型以及以上模型的组合或改进等[10]。在潜标定位过程中，水下设备与水面设备间的钟差产生原理与卫星钟差相似。故卫星钟差的预报模型对于水下时钟同步算法具有指导作用。

卫星钟差模型中最为常见、简便的是多项式模型中的二次多项式模型。此模型短期预报效果较好，物理意义明确。本文依据二次多项式钟差预报模型，推导了一种适用于水下声学系统的高精度同步时钟修正算法。该算法以高精度的差分GPS秒脉冲作为时钟基准源，以其大地坐标的位置作为水面设备的绝对位置；在水面实时监测水下设备的脉冲信号，并对其做数小时的精确测量；建立水下设备的时钟漂移模型，推演时钟误差修正量；将其代入解算方程，按照递归最小二乘法，计算时钟偏移量，并按照时钟漂移规律完成水下设备绝对时间的更新。最终通过实验数据验证，证明了本算法能有效解决水下设备与水面设备间的钟差补偿问题，实现设备间的时钟同步。

1 模型建立与仿真

1.1 模型建立

水下钟差是指在水下声学定位过程中，由于时钟频漂没有得到及时修正带来的潜标同步发射与GPS同步信号之间的时钟误差。误差主要来源为水下设备恒温晶振自身晶体和元件的老化，反映为时钟的偏移与漂移。

卫星钟差的二次多项式模型可以表示为[11]

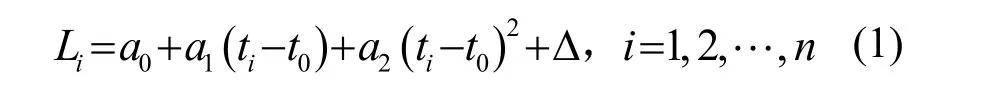
式中： Li表示ti时刻与GPS卫星的钟差，t0代表参考时刻；a0、a1、a2的物理意义分别为与卫星钟的钟差、钟速与频漂。钟差与钟速对应时钟偏移和时钟漂移，为线性变化部分。文献[12]也指出，短期内时钟频率漂移呈线性变化，故假设待修正钟差为线性模型。若此修正钟差的误差模型假设为

式中：te代表含有误差的时间；tr代表真实时间；k和b分别表示时钟漂移与时钟偏移，对应式(1)的a1与a0。假设信号发射周期为 m(单位：s)，由式(2)可推得真实时延公式为

式中：Toi为第i个时延观测值，Tri为第i个真实时延，i代表时延序号。

单点潜标的定位解算采用最小二乘法，最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配。以绕圈走航方式为例，若在不同时刻不同位置获得N个观测值，不考虑钟差时，根据最小二乘法潜标解算公式为

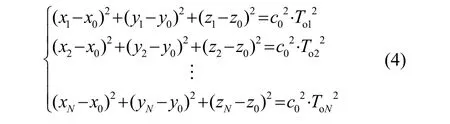
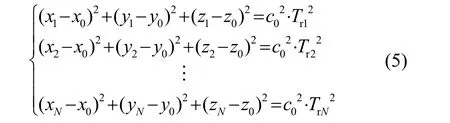
1.2 模型仿真

为证明模型的有效性，探究钟差给定位带来的误差影响，对模型进行仿真验证。假设海洋中无多普勒影响，声速固定且无海潮情况。取信号发射周期 m=6 s。系统测时误差、观测误差、声速测量误差分别在±5×10-5s、±0.1 m、±0.1 m·s-1的范围内均匀分布。具体步骤如下：

(1) 选取适当的绕行轨迹与固定潜标坐标。轨迹半径取1.5 km，误差在±15 m范围内均匀分布，按圆轨迹均匀取900个观测点，圆心处为潜标水平位置，水深为3 km，如图1所示；

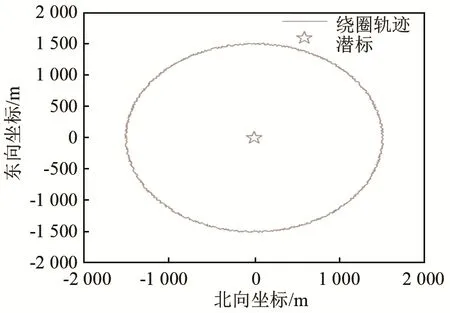
图1 仿真的绕行轨迹与潜标位置示意图Fig.1 Schematic diagram of simulated rounding track and submersible buoy’s position

(2) 用固定声速计算出每个轨迹点对应的时延，按照设想模型给时延附加上已设定误差参量的钟差。此处k按钟漂量级10-9～10-6s设置梯度值(若钟漂量级为10-9s，则k=1−10-9)，对应的b均设置为0.001 s；

(3) 分别用式(4)与包含钟差修正解算的式(5)对附加不同钟差的时延数据进行解算，并反算残差，计算定位精度。残差计算公式为

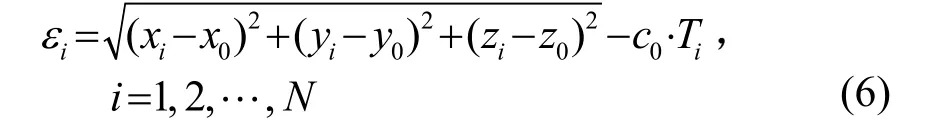
即观测点i的坐标与解算所得潜标坐标之间的距离与平均声速乘以相应时延的差值。其中εi代表每个观测点的反算残差。定位精度即为反算残差的均方根值，表示为

经以上步骤可得仿真结果，如图2所示。由图2可见解算所得钟差系数k与设定值基本保持一致，差值控制在10-9量级。参数b的解算误差保持在10-5s量级。修正前后定位精度变化如图3所示，尤其当钟漂量级变大时，定位精度得到了显著提高，修正后定位精度保持在0.1 m量级。修正前后的定位精度符合实际情况，证明了修正模型的有效性与准确性。

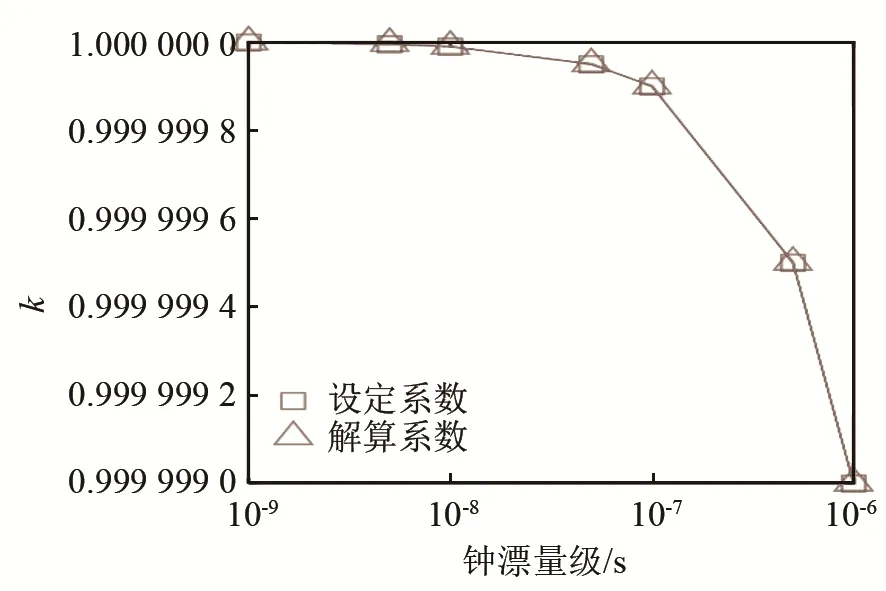
图2 模型系数k值对比曲线Fig.2 Comparative curve of model coefficient k

图3 钟差修正前后定位精度对比曲线Fig.3 Comparative curve of positioning accuracy before and after clock error correction

不同钟漂量级的无修正定位反算残差曲线趋势一致，以10-7s的钟漂量级为例，水下钟差对定位残差的影响趋势如图4所示。

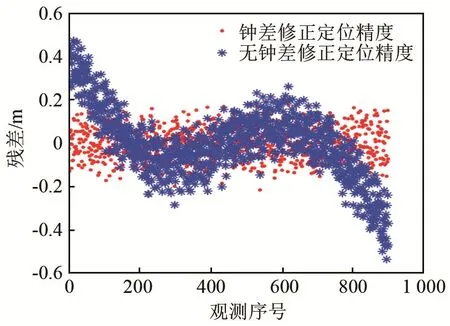
图4 有无钟差修正残差分布对比Fig.4 Comparison of residuals distribution with and without clock error correction

2 海试验证

用于此次验证的试验数据来源于2019年7月某海上试验，试验水深约为 3 km，绕圈半径约为1.5 km，在定位区域内任取一点作为原点，将轨迹与潜标的位置用相对坐标表示，潜标1与潜标2的位置与绕圈轨迹如图 5所示。在海底固定布放潜标，水面船接收同步声信号，测量接收时延，同时采集船舶的位置、姿态等参考信息。上述信息可精确计算接收点位置。其中测时精度为 50 µs；GPS水平精度为0.2 m，高程精度为0.5 m；观测误差为0.1 m；声速测量误差为0.1 m·s-1。

图5 海试数据得到的绕行轨迹与潜标位置示意图Fig.5 Schematic diagram of rounding tracks and submersible buoys’ positions from sea trial data

2.1 数据预处理

实验载体的坐标、姿态、航向等数据由GPS和姿态仪实时测定。已知接收阵元在载体坐标系下相对于GPS天线的坐标，将GPS、姿态等数据与阵元时延数据通过时间标对齐后，即可利用完备的数据，通过公式换算将阵元在接收时刻的坐标转换到大地坐标系下。对于时延数据和相应的换能器坐标进行预处理。选取相应潜标的绕圈轨迹与相应时延后，即可用最小二乘法解算；对于绕圈解算中的声速选取，平均声速法[13]具有良好的适用性。平均声速法本质上是适当选取一个等效声速，使它对应的等效传播时延等于真实的传播时延。采用在垂直线上取深度的平均来对声速进行修正，公式为

式中：为等效声速；ZH为潜标深度；Z0为目标深度；Cj为深度Zj时的声速。试验海域声速剖面如图6。设置相对声速梯度变化量门限为1×10-6m·s-1，将声速剖面等梯度分层。在此门限阈值下，得到700层等梯度声速。ZH为6.204 m，Z0预估为3 050 m，代入式(8)可解算得为1 495.7 m·s-1。

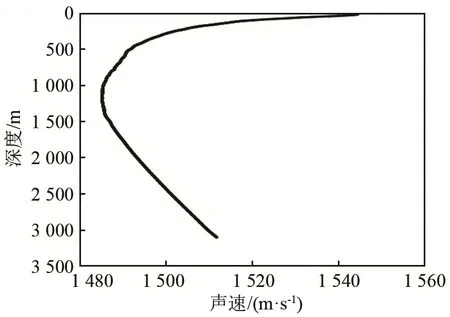
图6 试验海域声速剖面Fig.6 Sound velocity profile in the experimental sea area

2.2 模型验证

首先将处理后的数据代入无钟差修正的式(4)，分析残差表现与定位精度。两个潜标解算所得相对坐标及定位精度如表1所示。用定位结果推残差，如图7所示，图中散点为定位残差，平滑曲线表示残差趋势。

表1 两潜标的定位解算结果Table 1 The positioning results of two submersible buoys

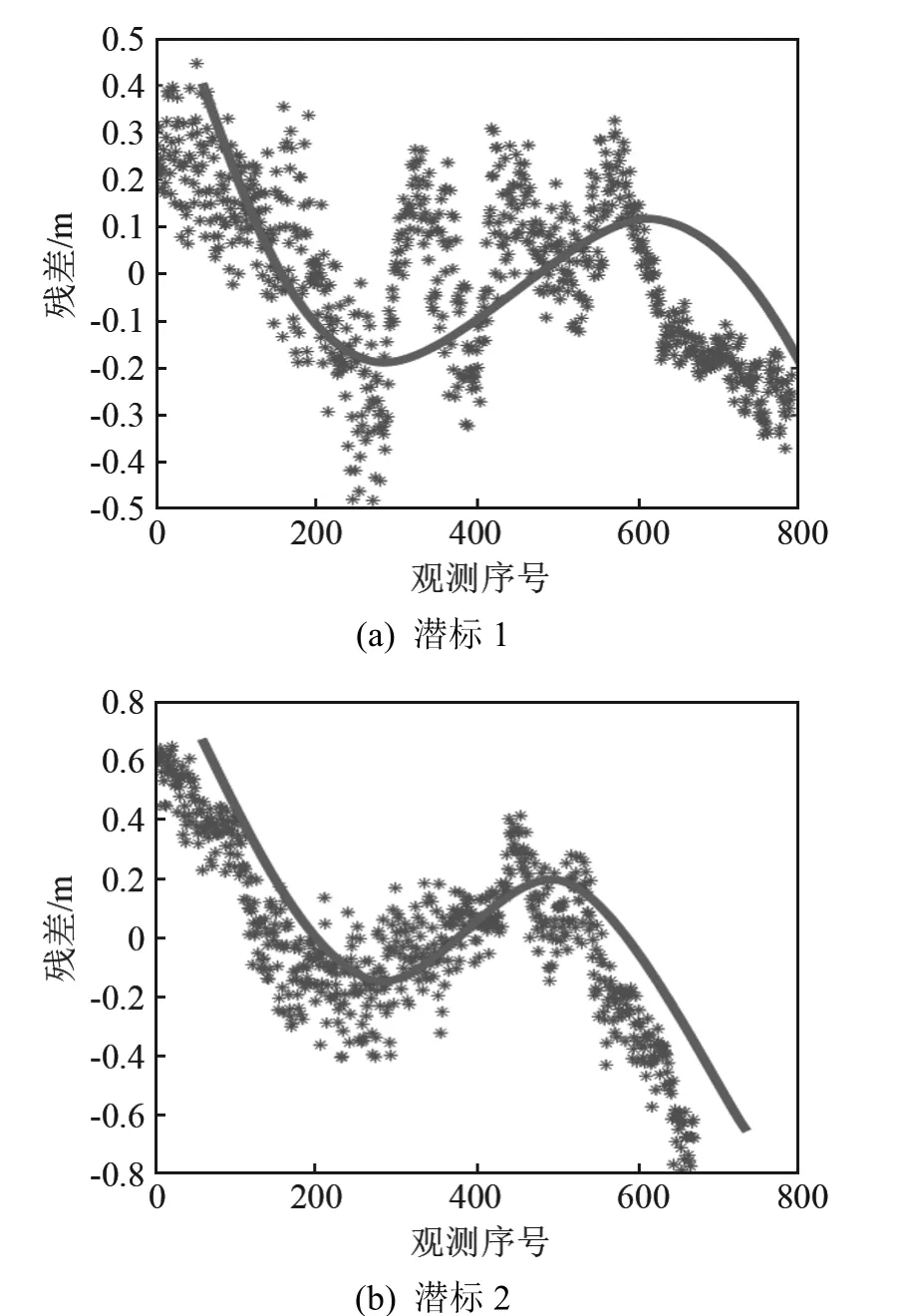
图7 两潜标定位结果反算残差Fig.7 The inversion residual of two submersible buoys’positioning results

观察两潜标的残差表现，发现均与图4中“无钟差修正残差分布”具有相似的趋势。可推测试验数据中所包含的钟差符合设想模型。故将数据代入式(5)进行解算，求得两个潜标的相对坐标、精度、及精度提高百分比如表2所示，钟差修正模型系数如表3所示。

表2 两潜标钟差修正解算结果Table 2 Two submersible buoys’ positioning results with clock error correction

表3 两潜标钟差修正模型系数Table 3 Clock error correction model coefficients for two buoys

两潜标的钟差修正前后对比如图8所示，可见残差趋势得到了有效修正。

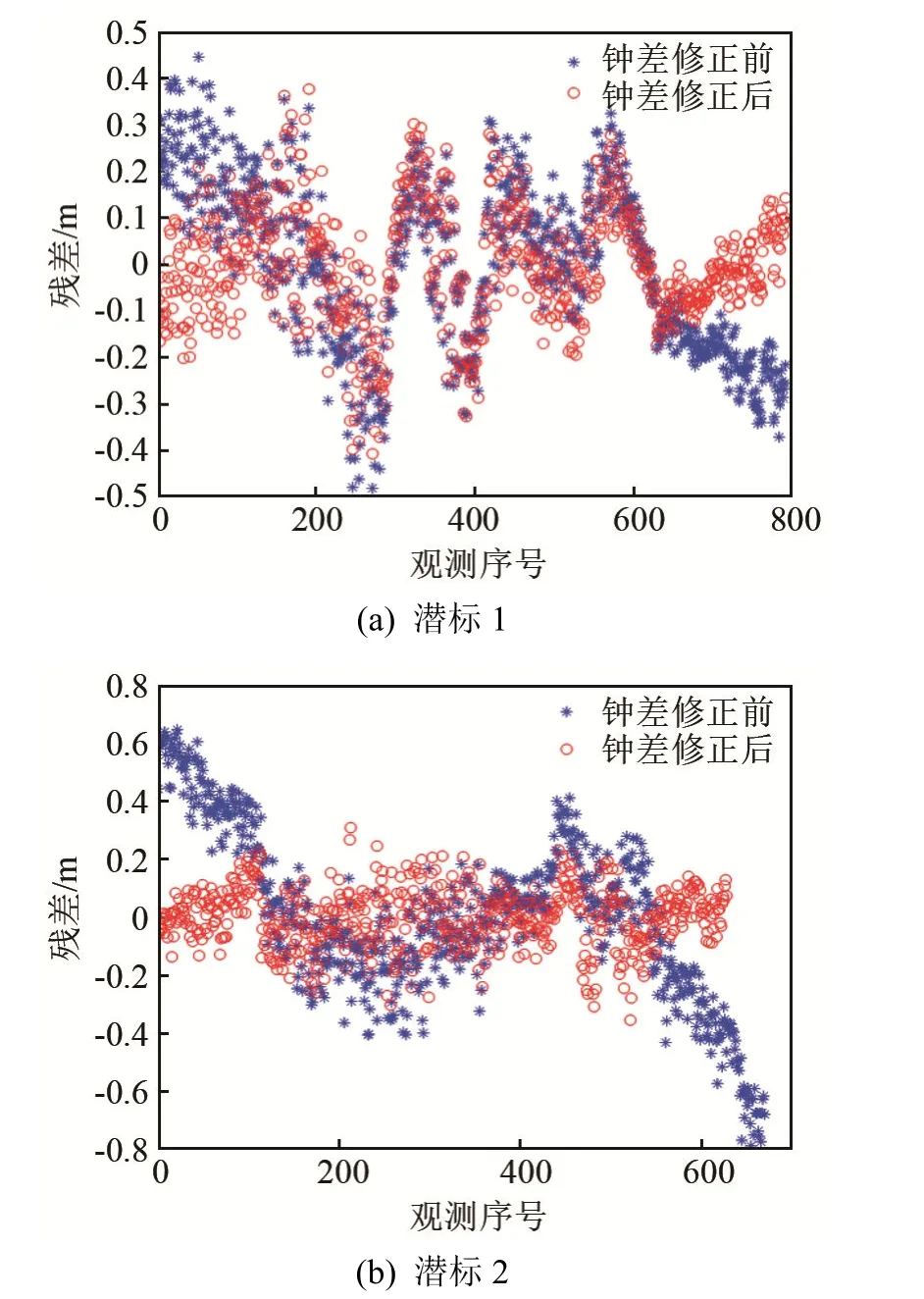
图8 两潜标钟差修正前后残差对比Fig.8 Comparison of residuals distribution before and after clock error correction for two submersible buoys

通过以上信息可知，钟差修正后定位精度得到了较明显提高，潜标1的定位精度提高了31.1%，潜标2的定位精度提高了64.6%；且解算所得模型系数与设备精度基本一致，证明了本文建立的钟差修正模型的有效性与准确性。

3 结 论

本文通过研究水下钟差产生机理，提出了适用于水下钟差修正的算法。通过仿真验证了模型的有效性及可行性。随后利用某海试数据对模型进行了进一步验证，两个潜标的定位精度较修正前分别提高了31.1%、64.6%，且解算钟差模型系数与设备参数一致，定位结果反算残差对比图也显示了修正效果，证明了算法的有效性与准确性。此模型算法对高精度水下固定点声学定位的研究具有推进作用，在钟差存在的情况下可有效提高其定位精度。

本算法为长基线导航中更为复杂的钟差修正提供了理论基础，后续可以以本文模型为依据进行研究；另外，理论上声速误差也是随时空变化的，在钟差修正中，亦包含了随时间变化各种误差的线性部分；潜标1修正后残差在0附近存在波动，而系统误差应满足正态分布，推测此波动为声速二次型部分带来的影响，有待进一步研究。