随机数据相干函数谱的归纳处理方法研究
2021-05-08邹学利张国强王刚张生鹏
邹学利,张国强,王刚,张生鹏
随机数据相干函数谱的归纳处理方法研究
邹学利,张国强,王刚,张生鹏
(航天科工防御技术研究试验中心,北京 100854)
研究相干函数谱的归纳处理方法,提高多点多轴振动试验对实际环境模拟的真实性。通过对相干函数统计分布规律的分析,提出一种基于实测数据的制定相干函数谱的统计容差法,考虑到相干函数对试验量级影响的特殊性,没有采用传统的容差上限分析法,而是对相干函数的容差区间进行分析,并给出相干函数容差上限谱和容差下限谱的制定方法。利用该方法对某型号产品的实测数据表明,该方法有效可行。采用容差区间估计法,降低了相干函数的试验值与实测值的误差,达到了提高试验环境对实际环境模拟真实度的要求。
多轴振动;多点激励;相干函数;归纳处理;统计容差法
随着航天产品对可靠性要求的提高,单轴单点激励试验由于其特有的局限性,逐渐无法满足试验需求。比如试验推力不足,产品在试验过程中的模态响应特性与真实环境差异较大,不能模拟多点输入的耦合特性和相关性等。多轴多点激励试验的出现,有效弥补了这些缺陷,因此越来越受到人们的重视。
长期以来,由于多轴振动试验谱的制定方法还不明确,导致多轴振动试验还不能很好地模拟实际飞行环境,这严重限制了多轴振动试验的应用与发展。基于实测数据的多轴振动试验谱的制定过程包括:随机振动数据的预处理、随机振动数据的时域转换、功率谱密度的归纳处理、相干函数的归纳处理。
预处理工作的目的是剔除数据中的虚假趋势及错点,并验证实测数据是否满足后续分析的基本条件,即各态历经的平稳随机过程。因此预处理工作主要有:去除趋势项[1-4]、错点剔除[5-6]、正态性检验[7]、平稳性检验[8]以及各态历经性检验[9]。
随机振动数据的时域转换[10]是将各遥测点的线性振动时域数据,转换为6个自由度的时域振动数据,即参考点的3个线振动和试验件绕坐标轴转动的3个角振动,基本分析是在时域用经典机械运动关系实现的。六自由度振动的时域数据是多轴振动试验谱归纳处理的基础。
目前,比较成熟的功率谱密度处理方法[11-17]有2种:极值包络法和统计容差法。极值包络法的缺点是没有根据数据样本数量和分布特性进行统计处理。统计容差法是振动数据归纳从传统的上限包络到统计概念进行归纳的突破。
随机数据的预处理、时域转换以及功率谱密度的归纳处理方法,很多文献都进行了大量的研究。相干函数谱的归纳处理方法目前还处于探索阶段,未见相关文献进行过类似的研究报道。文中对此进行了研究,并提出了一种基于统计容差法的相干函数谱的归纳处理方法。
1 两个随机变量相干函数的分布特性
互谱是反应两个信号在不同频率处相互关联程度的量。假设现有2个时域信号x和x,其互谱表达式为:

式中:γ为信号x和x之间的相干函数;θ为信号x和x之间的相位差,简称相位;S()为信号x的自谱;S()为信号x的自谱;S()为信号x和x之间的互谱。
相干函数是反映信号之间线性关系的函数,如果相干函数等于0,说明两个信号是完全不相干的,其对应的互谱也必然为0。如果相干函数等于1,说明两个信号是全相干的,此时的互谱幅值为:

根据式(1),相干函数的定义为:






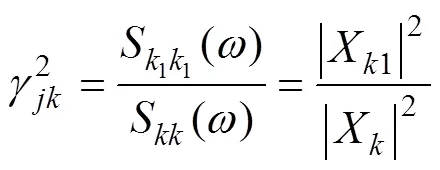
因此,x和x相干函数的另一种解读是:x中与x全相干分量的频谱幅值与x频谱幅值的比值。很容易证明,x和x的相干函数同样等于x中与x全相干分量的频谱幅值与x频谱幅值的比值。


F分布的极限分布为正态分布[18-19],且当自由度很大时,其方差很小[20-21]。当很大时,相干函数服从方差很小的正态分布,说明相干函数的取值非常集中,这一点与相干函数的特点(1≥γ≥0)是吻合的。F分布相较于2分布,收敛于正态分布的速度较慢,因此应进行较多的平均次数(增加自由度),才能保证后续分析结果的精确度。
2 相干函数的容差估计
相干函数不同于功率谱密度,它本身是线性相关性的描述,不代表越大越安全。因此不能简单分析其容差上限谱,还需要对其容差下限进行估计,得到其置信区间。
2.1 相干函数平方的包容区间
对于2个随机变量,其时域信号服从平稳的正态分布时,则其功率谱密度服从自由度为平均次数2倍的卡方分布。2个随机变量的相干函数的平方服从自由度(第一自由度和第二自由度相等)为平均次数2倍的F分布。


于是有:

式中:(1‒β)/2为标准正态分布的上侧分位点,满足(≥(1‒β)/2)(1‒)/2,服从标准正态分布。
也就是说2落在区间[‒(1-β)/2,+(1‒β)/2]以内的概率为,或者说区间[‒(1-β)/2,+(1‒β)/2]在概率上包含了·100%的数据,因此称为数据包容概率。一般应取大一些,记:

式中:χ1和χ2分别为数据2的包容概率为的容差上限和容差下限。
2.2 均值μ的容差上、下限估计



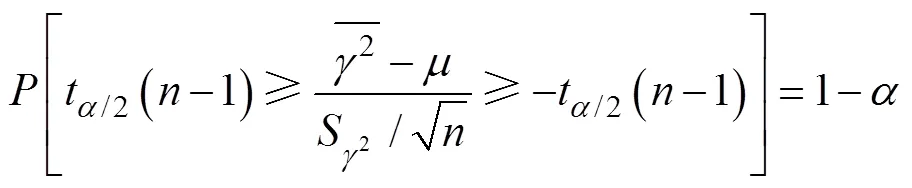
于是有:

因此均值在置信度为(1‒)的置信上限(容差上限)c1和置信下限(容差下限)c2分别为:

式中:t/2(‒1)表示自由度为(‒1)的分布的/2分位点。
2.3 标准差σ的容差上、下限估计
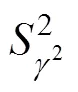



于是有:

因此标准差在置信度为(1‒)的置信上限(容差上限)c1和置信下限(容差下限)c2为:

2.4 相干函数的容差上、下限估计
相干函数的容差上、下限可表示为:
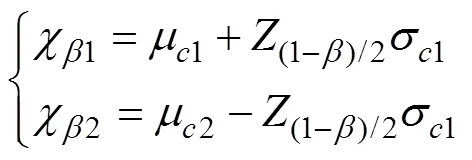

式(22)可以简写为:

式中:22为相干函数的容差系数,表达式为:

相干函数的容差上下限估计为:

式(25)即为相干函数容差上、下限谱的计算公式。
容差上、下限谱都为实测谱,没有经过平直处理,50%、90%置信度下,相干函数容差限系数与统计自由度的关系如图1所示。可以看出,在其他条件相同的情况下,容差限系数随着自由度的增加而变小,随置信度的增加而变大,随包容概率的增加而变大。值得注意的是,相干函数在0~1之间。如果计算得到的容差上限大于1,则直接取1即可;如果计算容差下限时,得到根号下的值为负值的话,直接取容差下限值为0。

图1 不同置信度下容差系数与统计自由度的关系
3 相干函数规范谱的上下限估计
3.1 频率段划分

检验假设为“谱线1和2的相干函数值属于同一总体”。因为相邻谱线都属于正态分布,所以只要检验它们具有相同的均值和方差即可,作如下统计量:
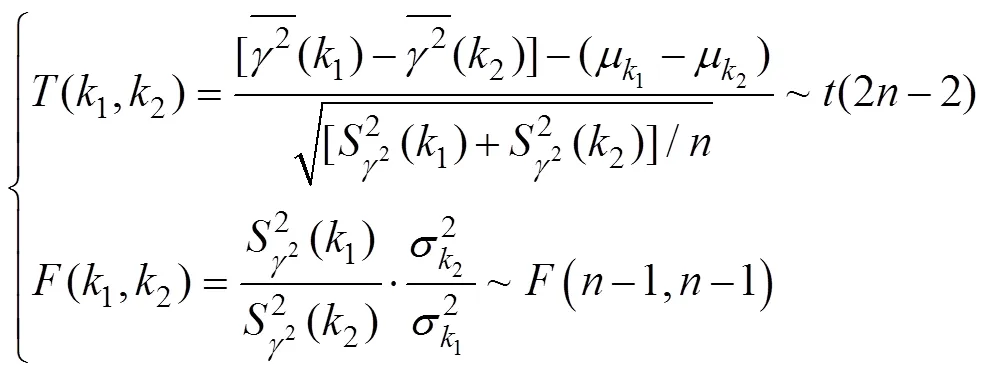

在给定显著性水平下,可得到各自的接受域为:

如果计算得到的(1,2)和(1,2)分别落在各自的接受域内,则谱线1和2的相干函数属于同一总体。
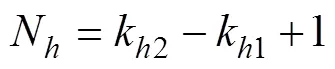
3.2 频段内相干函数平直谱的估计
将频段内所有谱线的样本归并,样本量等于各谱线样本量的总和,然后按照统计容差法得到频段的容差上限,该容差上限即为频段的平直谱估计。
按式(29)对频段内的数据进行均值和方差估计:

根据前面的分析,置信度为(1-),数据包容概率为的容差限系数为:

于是,相干函数在频段内平直谱的容差上、下限估计为:

在线性坐标系下,用直线将各频段内的平直谱首尾相连,即可得到置信度为(1-)、数据包容概率为的相干函数规范谱的容差范围。实际试验时,只要将相干函数控制在容差范围内即可。
4 某飞行器遥测数据的多轴试验谱估计
某飞行器在空军训练试验基地完成了飞行试验,试验过程中对飞行器的振动、冲击环境进行了测量。安装了4只力学传感器,共测量了8组参数。利用8组遥测数据进行五自由度(除了绕轴向转动的自由度以外的5个自由度)多轴振动试验谱的分析。
发动机工作时间段大约为1.4~15 s左右,10~ 14 s内的振动量级较大,因此将此段数据作为样本进行分析。经过预处理和时域转换后,得到五自由度的时域信号,如图2所示。在此基础上,进行五自由度的功率谱密度分析以及不同自由度之间的相干函数分析。

图2 五自由度随机振动时域曲线
在进行相干函数容差上、下限估计时,首先将如图3所示的时域数据分成若干段,对不同自由度之间相同时间段的数据进行相干函数估计,并作为样本,按照前面给出的方法即可得到相干函数的容差上、下限谱。一般来说,样本数越多,分析结果的可信度越大。但样本数受到原始数据的长度限制,如果单纯追求样本数而导致每个样本的数据长度过小,不能进行充分平均,反而影响容差谱的分析精度,因此需要均衡考虑。
相干函数的容差上、下限谱分析结果如图3所示,包容概率为99%(=0.99),置信度为50%(=0.5)。图4中,波浪线为样本曲线,平直的水平线分别为容差上、下限谱。5个自由度相互之间的相干函数共有10个。

图3 相干函数的容差谱
规范谱分析结果如图4所示,粗实线为容差上、下限,细实线为对应上、下限的规范谱。从曲线的变化趋势可以看出,相干函数都应该是平直谱。由于样本数据的长度较短,平均次数不足,相干函数曲线波动较大,因此在处理规范谱时,没有考虑曲线的变化,直接按照平直谱进行了处理,这样的可信度更高一些。取上下限的均值作为试验设置条件,并将上下限作为容差进行设置,见表1。
表1 相干函数值

Tab.1 Values of coherent functions
5 结语
首先对相干函数的分布规律进行了研究,并证明了相干函数服从F分布。由于F分布的极限分布是正态分布,因此当平均次数足够时,相干函数将服从方差很小的正态分布。该项研究结果,使统计容差法可以应用于相干函数谱的归纳处理过程。
在相干函数处理的过程中,根据相干函数的特点,没有采用功率谱密度容差上限谱分析的方法,而是提出了容差区间的概念,即估计相干函数的容差上限谱和容差下限谱,并要求试验过程中,将相干函数控制在容差区间内。

图4 相干函数的规范谱
[1] 吴夏平, 王福明. 基于最小二乘法原理的趋势项处理研究[J]. 微计算机信息, 2008, 24(3): 254-255. WU Xia-ping, WANG Fu-ming. The research of trend remove based on the principle of least-squares method[J]. Microcomputer information, 2008 , 24(3): 254-255.
[2] 王广斌, 刘义伦, 金晓宏, 等. 基于最小二乘原理的趋势项处理及其MATLAB的实现[J]. 有色设备, 2005(5): 4-8. WANG Guang-bin, LIU Yi-lun, JIN Xiao-hong, HE Yu-hu. Treatment of tendency part and its MATLAB accomplish-ment based on least-square principle[J]. Non-ferrous Metallurgical Equipment, 2005(5): 4-8.
[3] 朱学锋, 韩宁. 基于小波变换的非平稳信号趋势项剔除方法[J]. 飞行器测控学报, 2006, 25(5): 81-85. ZHU Xue-feng, HAN Ning. Removal of trend from non-stationary signal based on wavelet transformation[J]. Journal of spacecraft TT & C technology, 2006, 25(5): 81-85.
[4] 张庆华, 王太勇, 徐燕申. 小波分析在压缩机噪声信号去除趋势项处理中的应用[J]. 中国制造业信息化, 2003, 32(2): 114-116. ZHANG Qing-hua, WANG Tai-yong, XU Yan-shen. Application of wavelet analysis in noise signal of compressor[J]. Chinese manufacturing informatization, 2003, 32(2): 114-116
[5] 赖素建, 靳晓雄, 彭为, 等. 信号预处理中错点剔除方法的研究[J]. 佳木斯大学学报, 2011, 29(3): 333-336. LAI Su-jian, JIN Xiao-xiong, PENG Wei, et al. Research on the method to reject abnormal data in signal preprocessing[J]. Journal of Jiamusi University, 2011, 29(3): 333-336.
[6] 俞钟行. 拉依达准则用于剔除物探数据中的坏值[J]. 物探与化探, 1989, 13(3): 238-240. YU Zhong-xing. The Layida Criterion used to get rid of bad values in data of geophysical prospecting test[J]. Geophysical and geochemical exploration, 1989, 13(3): 238-240.
[7] CHEN Guang-lei, CUI Heng-jian. The testing for normality based on PP-Skewness and PP-Kurtosis in EV model[J]. Mathematica applicata, 2004, 17(1): 16-21.
[8] 乔新愚, 肖建红, 郑术力. 随机振动的描述方法及稳态检验[J]. 电子质量, 2006(6): 33-35. QIAO Xin-yu, XIAO Jian-hong, ZHENG Shu-li. The description of random vibration and steady status check[J]. Electronics quality, 2006(6): 33-35.
[9] 陈小锋, 徐瑞. 大跨度桥梁抖振响应平稳性和各态历经性检验[J]. 中外公路, 2010, 30(3): 126-128. CHEN Xiao-feng, XU Rui. Test of buffeting response stability and ergodicity of long span bridges[J]. Journal of China & foreign highway, 2010, 30(3): 126-128.
[10] MIL-STD-810G-527, 多激振器试验方法[S]. MIL-STD-810G-527, Multi exciter test method[S].
[11] GJB/Z 126—99, 振动、冲击环境测量数据归纳方法[S]. GJB/Z 126—99, The inductive methods for environmental measured data of vibration and shock[S].
[12] GB 10593. 3—90, 电工电子产品环境参数测量方法振动数据处理和归纳方法[S]. GB 10593. 3—90, The measure methods for environmenta parameters of electronic-electrical products the inductive methods for vibration data [S].
[13] HB/Z 87—84飞机飞行振动环境测量数据的归纳方法[S]. HB/Z 87—84 The inductive methods for environmental measured data of aircraft flying [S].
[14] 徐明. 随机振动环境测量数据归纳的统计容差方法[C]// 2001年中国航空学会环境工程学会学术年会文集. 北京: 中国航空学会, 2001. XU Ming. The statistical tolerance method for environmental measured data of random vibration[C]// Proceedings of the 2001 annual meeting of the Society of Environmental Engineering, CAAC. Beijing: CAAC, 2001.
[15] 马升, 徐明. 振动环境试验条件的确定[J]. 航空标准化与质量, 2004(2): 38-43. MA Sheng, XU Ming. Determination of vibration environment test conditions[J]. Aeronautic standardization & quality, 2004(2): 38-43.
[16] 穆立茂, 黄海英, 张靖, 等. 车载物资振动环境谱的数据处理与归纳[J]. 装备环境工程, 2010, 7(1): 75-77. MU Li-mao, HUANG Hai-ying, ZHANG Jing, et al. Data processing and induction of vibration environmen spectrum for commodity carried on truck[J]. Equipment environmental engineering, 2010, 7(1): 75-77.
[17] 袁宏杰, 罗敏, 姜同敏. 随机振动环境测量数据归纳方法研究[J]. 航空学报, 2007, 28(1): 115-117. YUAN Hong-jie, LUO Min, JIANG Tong-min. Study on Inductive Method for Environmental Measured Data of Random Vibration[J]. Acta aeronautica Et astronautica sinica, 2007, 28(1): 115-117.
[18] 曾珍, 张宇.2分布、分布、F分布与正态分布间的关系[J]. 湖北师范学院学报(自然科学版), 2015, 35(3): 62-65. ZENG Zhen, ZHANG Yu. The relationship between the2distribution、distribution、F distribution and normal distribution[J]. Journal of Hubei Normal University (Natural Science).
[19] 李开灿, 孟赵玲.2分布、分布和F分布的一致渐近正态性[J]. 北京印刷学院学报, 2004, 12(3): 30-33. LI Kai-can, MENG Zhao-ling. The Uniformly Asymptotic Normality of the2-distribution,-distribution and F-distribution[J]. Journal of Beijing Institute of Graphic Communication, 2004, 12(3): 30-33.
[20] 刘晓鹏, 刘坤会. F分布密度函数之性质[J]. 应用概率统计, 2005, 21(3): 304-314. LIU Xiao-peng, LIU Kun-hui. The property of f distribution density funetion[J]. Chinese journal of applied probability and statisties, 2005, 21(3): 304-314
[21] LI Kai-can, LIU Da-fei. A way of asymptotic normality for the matrix f-distribution[J]. J of Math (PRC), 2011, 31(6): 1063-1073.
Research on Inductive Method of Random Data Coherence Function Spectrum
ZOU Xue-li, ZHANG Guo-qiang, WANG Gang, ZHANG Sheng-peng
(China Aerospace Science & Industry Corp Defense Technology R & T Center, Beijing 100854, China)
In order to study the inductive method of coherence function spectrum and improve the authenticity of multi-support and multi-axial vibration test on simulating real environment.By analyzing the statistical distribution law of coherence function, this paper proposes a statistical tolerance method based on measured data to formulate coherence function spectrum. Because of the particularity of the influence of coherence function on the experimental magnitude, the tolerance interval of coherence function is analyzed instead of the traditional method of analyzing upper limit of tolerance, and the method of upper and lower tolerance spectra of coherence function are given.The experimental data of a certain type of product shows that the method is effective and feasible. By using the method of tolerance interval estimation, the error between the experimental value and the measured value of the coherence function is reduced, and the requirement of improving the authenticity of the experimental environment to the actual environment simulation is achieved.
multi-axis vibration; multi-support excitation; coherence function; inductive method; statistical tolerance method
2020-09-03;
2020-10-20
ZOU Xue-li (1973—), Male, Master, Senior engineer, Research focus: environmental and reliability test technology research.
张国强(1984—),男,硕士,高级工程师,主要研究方向为超声检测。
Corresponding author:ZHANG Guo-qiang (1984—), Male, Master, Senior engineer, Research focus: ultrasonic testing.
邹学利, 张国强, 王刚, 等. 随机数据相干函数谱的归纳处理方法研究[J]. 装备环境工程, 2021, 18(4): 088-095.
10.7643/ issn.1672-9242.2021.04.013
2020-09-03;
2020-10-20
十三五装备预研联合基金(6141B070204)
Fund:United Fund for Equipment Pre-Research(6141B070204)
邹学利(1973—),男,硕士,高级工程师,主要研究方向为环境与可靠性试验。
TB114
A
1672-9242(2021)04-0088-08
ZOU Xue-li, ZHANG Guo-qiang, WANG Gang, et al. Research on induction treatment method of random data coherence function spectrum[J]. Equipment environmental engineering, 2021, 18(4): 088-095.
