基于结构应变监测的风帆推力测量方法研究
2021-05-08杨华伟汪雪良张涛陈立徐春郑庆新
杨华伟,汪雪良,张涛,陈立,徐春,郑庆新
基于结构应变监测的风帆推力测量方法研究
杨华伟1,2,汪雪良1,2,张涛1,2,陈立3,徐春1,2,郑庆新1,2
(1.中国船舶科学研究中心,江苏 无锡 214082;2.南方海洋科学与工程广东省实验室(广州),广州 511458;3.大连船舶重工集团设计研究院有限公司,辽宁 大连 116021)
提出一种用于实船测量的风帆推力测量方法。针对VLCC风帆推力实船测量的需求,首先对风帆推力计算公式和风帆桅杆推力状态进行分析,进一步根据梁结构应变测试方法提出基于应变监测的风帆推力测量方法和传感测点布置方案。通过陆基模拟试验对风帆推力测量方法进行试验验证。传感测点间结构应变差值随风帆推力增加而增大,具有显著线性关系,线性相关系数为0.9965,测试风帆推力与实际推力之间的平均误差为5%。提出的风帆推力测量方法用于实船测量是切实可行的。
风帆助推装置;应变监测;风帆推力;测量方法;测试推力
随着全球气候变暖和人们环境保护意识的增强,各个行业对清洁能源应用技术的需求比以往任何时候都更加迫切,对于船舶远洋运输行业更是如此。船舶远洋运输在世界货物贸易中起到了非常大的作用,与其他交通工具相比,货物运输占比最高,然而大型船舶在航行过程中消耗的能源也是巨大的,如何降低船舶运行能耗和采用新型节能推进技术一直是船舶研究和设计者的研究重点。风帆助推技术是一种利用风能作为清洁能源产生船舶前进动力的技术,与其他技术相比,具有显著的安全性和高效性等特点[1-5]。
风帆助推船最大的优点是节能,通过作用于风帆上的推力为船舶提供前进辅助动力。风帆产生的纵向推力大小是评价风帆船节能效果的重要指标,有研究者通过风洞模型试验证明了在合理操帆情况下,船舶最大节能效果可达5%以上,航速可增加3%[6-8]。对于风帆助推船舶模型,风洞模型试验可以测试风帆推力,并评价风帆助推装置的节能效果;对于航行中的船舶,除通过基于风洞试验系数的计算公式计算风帆装置产生的推力外,目前还没有长期可用的实船风帆助推装置推力测量方法[9]。另外,在风帆助推装置推力系数风洞试验中,由于风帆助推装置模型结构的尺寸较小,风帆模型推力是通过连接船体模型与转动机构的测力元件获得的[6]。对于数万吨的实船,采用测力元件连接船体和桅杆转动机构是不现实的。因此,研究可用于实船的风帆纵向推力测量方法是很有必要的,具有重要的工程意义。
当前,基于结构应变的健康监测技术被广泛应用于大型结构物(如桥梁、船舶、潜水器、大坝、铁路等)的长期连续在线监测,为大型工程结构的安全使用、后期维修及新型结构形式的科学研究起到了重要作用[10-11]。例如,苏通大桥结构的健康监测,验证了索塔群桩基础的所有监测点均无涉及桩基础安全性的异常信号,通过对有限元计算和离心模型试验结果,得到了桩基础实测沉降和差异沉降值偏小的结论[12]。另外,江阴长江大桥在建桥初期就建立了结构安全健康监测系统,其主要目的是应用现代传感测试技术、计算机技术、现代网络通讯通信技术对桥梁的工作环境、结构状态,对在各类外部荷载因素作用下的响应进行实时监测,以便及时掌握桥梁的结构状态,全面了解桥梁的运营条件及质量退化状况,为桥梁的运营管理、养护维修、可靠性评估提供了依据[13]。与其他技术相比,结构健康监测技术可以利用传感器对某一对象进行长期连续的监测,而不是单次检测,具有显著的实时性特征,因此利用该种监测技术对风帆装置纵向推力进行连续测量具有较强的工程可实现性[14-15]。
1 风帆推力
风帆纵向推力(沿船舶前进方向的合力)是沿船长方向的作用力,用T表示,计算公式为[1,9]:

式中:FT为推力系数;A为船速和自然风的合成速度,m/s;为风帆总面积,m2;为空气密度,kg/m3。
由式(1)可知,纵向推力T由FT、A、、共4个参数确定,其中风帆总面积为固定值,FT由风洞模型试验获得,也为固定量,合成速度A和空气密度为动态变化量,含2个变量。推力系数FT需通过风帆助推船模型风洞试验或数值计算获得,依赖于风洞试验或数值建模计算。对于没有经过风洞试验或数值建模计算的风帆助推装置,则不能通过式(1)计算出风帆产生的推力大小。另外,风洞试验采用的是缩比模型,通过试验获得的推力系数与实船推力系数相比,可能会存在较大差异。利用式(1)计算得到的风帆助推装置推力的准确性较难评价,不利于风帆节能效果的及时评估。
2 风帆推力测量原理
由文献[1,16-18]可知,风帆助推船舶在海上航行时,风力载荷会产生沿船舶前进方向的合成推力和横倾力,推力与横倾力互相垂直。如图1所示,风力载荷通过风帆将纵向推力传递至船体甲板,从而推动船体前进。当风力垂直于帆面时,推力最大[19]。文中规定沿船长方向为轴,船宽方向为轴,船体高度方向为轴。图1中为风帆弦长,为翼型拱度,n为风帆展长,0为风帆几何中心距离甲板的高度。

图1 风帆助推装置推力分析
由结构力学知识可知[20],纵向推力T会在船体甲板至力作用点之间的风帆桅杆中产生弯矩。设距离船体甲板高度处的弯矩用表示,帆翼几何中心与甲板之间距离用0表示,则风帆桅杆距离甲板高度为1处的弯矩1可表示为:

由材料力学可知,弯矩与结构应变之间的关系为:

式中:为构件抗弯截面系数;为材料弹性模量;为构件应变。
将式(3)代入式(2),可得:

式中:1为桅杆1位置处的结构应变,随风力载荷变化。
式(4)中存在两个变量1、0,因此采用该式计算风帆纵向推力时,需采用不同类型的传感器监测结构应变和风帆高度。为降低实船监测复杂度,需将风帆高度变量0消去。
风帆桅杆距离甲板高度2处的弯矩2可表示为:

式(2)减式(5)得:

式中:0为桅杆断面z与z之间的距离,m。
则风帆纵向推力可进一步表示为:

将式(3)代入式(8)得:

式(8)中仅存在单一变量Δ,因此分别在风帆桅杆相距固定值为0的两断面处布置单向应变传感器,由应变监测系统采集应变数据,并将实时应变差值Δ代入式(8),即可在线计算出风帆桅杆纵向推力。该测量方法不受风帆装置帆翼升降高度的影响。
3 测点布置方案
风帆推力测量对象为VLCC上左右舷横向对称布置的风帆助推装置,风帆高39.68 m,宽14.8 m,共3节。表1、2分别列出了VLCC及风帆助推装置的主要参数[6]。风帆助推装置实物如图2所示。
根据风帆推力测量原理,应变传感器应布置于风帆桅杆垂直于纵向推力的一个侧面上。考虑到应变测量的灵敏性,靠近船体甲板部位的结构应变最大,因此将应变传感器布置于风帆桅杆位于底部的第一节。由风帆纵向推力计算式(8)可知,两个应变传感器的应变差值是唯一变量。在同样风载作用下,两个应变测点的应变差值越大,推力测量值就越灵敏。由材料力学可知,两个应变测点之间的应变差值与两者之间的距离成正比。另外考虑到结构应变监测系统的固有测量误差,在距离过小的情况下,有可能出现应变测量差值为0或负值的情况,造成推力测量结果误差较大,因此两个应变测点之间的距离应尽量远一些。综合考虑桅杆尺度、基座根部应力分布状态和结构应变监测系统测量误差,将第一个应变传感器布置于桅杆距离基座上方3 m处,第二个应变传感器布置于基座上方6 m处。风帆推力应变测点布置方案如图3所示, S1、S2为两个单向应变传感器,应变传感器中心线与桅杆迎风面中心轴重合。
表1 VLCC主要参数

Tab.1 The main parameters of VLCC
表2 风帆助推装置主要参数

Tab.2 The main parameters of sail booster

图2 左右舷横向对称布置的风帆
4 陆基推力模拟试验
通过陆基推力试验模拟推力载荷垂直作用于应变传感器所布置侧面的工况,同时测量出应变测点位置处的结构应变。陆基模拟试验加载方案如图4所示,试验设备由风帆桅杆实物、三角形载荷转换连接板、钢丝绳、支架、滑轮和配重块组成。三角形载荷转换板通过焊接方式固定在风帆桅杆的中轴线上。钢丝绳与载荷转换板连接,将重物块产生的集中载荷转换为作用于桅杆中轴线上的线载荷,模拟风帆作用于桅杆中轴线上的线载荷。钢丝绳与水平地面夹角为,配重块悬挂于钢丝绳垂直部分尾端,通过配置不同吨位的配重块实现分级加载。由于试验所用桅杆为VLCC风帆助推装置桅杆实物,桅杆陆基固定方法与实船甲板安装相同,因此模拟加载时所测结构应变就是风帆装置桅杆的真实应变。陆基模拟试验前,按照风帆推力测点布置方案在风帆助推装置第一节桅杆迎风面布置2个单向应变传感器,传感器编号分别为S1、S2,两应变传感器间实测距离为3 m。

图3 风帆推力应变测点布置(单位:mm)

图4 陆基模拟试验加载方案
试验过程中,按照0、10、50、100 kN顺序加载。重物加载期间,由结构应变测试系统连续采集结构应变数据,不同载荷阶段采集到的结构应变序列曲线如图5所示。表3列出了S1、S2应变测点在不同吨位时的应变测量平均值和差值。
表3 载荷应变数据

图5 S1、S2测点应变序列曲线
Fig5 The strain sequence curve of S1 and S2
5 数据分析
由图5应变采样序列曲线可以看出,随着加载吨位的增加,S1、S2测点应变测量值不断增大,呈阶梯状;S1、S2应变差值也随着载荷吨位增加而逐渐增大,载荷吨位越大,两个传感器之间的应变差值也越显著,与式(8)反映的函数关系相一致。
由陆基模拟试验加载方案可知,作用于风帆桅杆迎风面的纵向推力与加载配重块重力产生的拉力并不相等,由加载重物块重力产生的纵向推力T为:
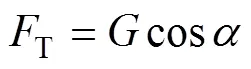
式中:为加载重物块重力,N;为斜拉钢丝绳与水平地面的夹角。
根据式(9),可以计算出重物块0、10、50、100 kN对应的风帆桅杆纵向推力分别为0、10 cos、50 cos、100 coskN。
将传感器测点S1、S2应变差值Δ代入式(8),可得到相应的推力测试值,见表4。由于、为常数,如果用2/3等价代换10 cos,则11/3、19/3对应的推力量化值可分别表示为55cos、95coskN,列于表4中,表4也列出了实际推力载荷和测试误差。
表4 试验测量推力与实际载荷对比

Tab.4 Comparison of test calculated thrust and actual load
由表4所列数据可以看出,由应变传感器S1、S2测得的风帆桅杆纵向推力载荷与实际加载载荷之间的最大误差为10%,平均误差为5%,且实际纵向推力与应变差值之间具有显著的线性关系。经计算,线性相关系数为0.9965。这表明基于结构应变监测的桅杆推力测量方法给出的风帆推力结果是可信的,能够及时给出风帆产生的纵向推力值。
6 结论
文中通过风帆助推装置推力计算公式各参数分析和风帆桅杆推力状态分析,基于结构应变监测技术提出了一种不依赖风帆助推船舶模型风洞试验的风帆推力测量方法,给出了VLCC实船风帆装置推力测量原理和应变传感器测点布置方案,通过风帆桅杆陆基模拟试验验证了测量方法的正确性。通过研究得出了以下结论:
1)基于结构应变监测的风帆推力测量方法能够实时给出风帆桅杆纵向推力值,方法简便可行。
2)由于采用实船监测数据,与其他方法相比,推力测量结果可信度更高。
3)由于该方法采用两个应变传感器的差值计算桅杆推力,因此不受风帆升降高度限制,具有普适性。
4)该方法可实现对没有经过风洞试验的风帆助推装置产生的纵向推力测量。
文中仅对风帆推力与传感器所在桅杆平面垂直工况进行了研究,对于其他任意角度工况下的风帆装置纵向推力的测量方法还需要进一步开展研究。研究成果可为任意风帆角度下推力测量研究提供参考。
[1] 于小虎. 风帆助航节能应用研究[D]. 大连: 大连海事大学, 2011. YU Xiao-hu. Study on application of energy-saving of sail-assisted ship[D]. Dalian: Dalian Maritime University, 2011.
[2] 何建海, 胡以怀, 张建霞, 等. 风能在船舶上的应用现状及展望[J]. 船舶工程, 2013, 35(5): 112-115. HE Jian-hai, HU Yi-huai, ZHANG Jian-xia, et al. Current situation and prospect of wind energy application on ship[J]. Ship engineering, 2013, 35(5): 112-115.
[3] DON W. Under way on wind power: Sail-assisted ships[J]. United States Naval Institute, Proceedings, 2019, 145(11): 332-335.
[4] 汪洋, 王志华, 陈爱国. 风帆助航的研究与应用综述[J]. 广州航海学院报, 2017, 25(1): 5-8. WANG Yang, WANG Zhi-hua, CHEN Ai-guo. Overview on the study and applications of propulsion with sail assistance[J]. Journal of Guangzhou Maritime Institute, 2017, 25(1): 5-8.
[5] 陈纪军. 风帆助推船舶操纵性预报研究[D]. 无锡: 中国船舶科学研究中心, 2011. CHEN Ji-jun. Study on prediction for the maneuverability of a sail-assisted ship[D]. Wuxi: China Ship Scientific Research Center, 2011.
[6] 陈纪军, 潘子英, 宋长友, 等. VLCC风帆船不同操帆模式下的节能收益评估[J]. 中国造船, 2016, 57(1): 169-176. CHEN Ji-jun, PAN Zi-ying, SONG Chang-you, et al. Evaluation of energy savings for a sail-assisted vlcc under different sail attack angle strategies[j]. Shipbuilding of China, 2016, 57(1): 169-176.
[7] ZENG Xiang-ming, ZHANG Hua-wu. Experimental study of the aerodynamics of sail in natural wind[J]. Polish maritime research, 2018, 25(s2): 17-22.
[8] 陈鲁愚, 陈顺怀, 严新平. 大型远洋风帆助航船舶节能效率分析[J]. 船海工程, 2010, 39(6): 121-123. CHEN Lu-yu, CHEN Shun-huai, YAN Xin-ping. Analysis on energy conservation of sail-assisted ocean-going vessel[J]. Ship & ocean engineering, 2010, 39(6): 121-123.
[9] 于升杰, 谢英亮, 周桂华, 等. 基于EEDI能效指数的船舶风帆助航能效[J]. 中国航海, 2017, 40(3): 125-128. YU Sheng-jie, XIE Ying-liang, ZHOU Gui-hua, et al. Energy saving of propulsion with sail assistance in terms EEDI[J]. Navigation of China, 2017, 40(3): 125-128.
[10] GARY F, CHRIS M, CHRIS R. Naval surface ship in-service information exploitation[J]. Procedia CIRP, 2013, 11: 92-98.
[11] 史红梅, 余祖俊, 朱力强, 等. 高速铁路无缝钢轨纵向位移在线监测方法研究[J]. 仪器仪表学报, 2016, 37(4): 812-816. SHI Hong-mei, YU Zu-jun, ZHU Li-qiang, et al. Study on the monitoring method of longitudinal displacement for the high-speed continuous welded rail[J]. Chinese journal of scientific instrument, 2016, 37(4): 812-816.
[12] 许映梅. 苏通大桥结构健康监测实践与思考[J]. 公路, 2013, (5): 65-70. XU Ying-mei. The practice and thinking of structural health monitoring for Sutong Bridge[J]. Highway, 2013, (5): 65-70.
[13] 韩惠婷, 缪长青, 李爱群, 等. 江阴大桥原结构安全监测系统设计分析与反思[J]. 特种结构, 2007, 24(2): 74-79. HAN Hui-ting, MIAO Chang-qing, LI Ai-qun, et al. The design and analysis of original structural health monitoring system of Jiangyin Bridge[J]. Special structures, 2007, 24(2): 74-79.
[14] 赵霞, 袁慎芳. 小型化结构健康监测实时信号分析模块[J]. 仪器仪表学报, 2004, 25(6): 832-835. ZHAO Xia, YUAN Shen-fang. The miniaturization of real-time wavelet analysis module for structure health monitoring[J]. Chinese journal of scientific instrument, 2004, 25(6): 832-835.
[15] 杨华伟, 万正权. CAN总线在船舶结构安全监测系统中的应用[J]. 电子测量与仪器学报, 2014, 28(5): 553-559. YANG Hua-wei, WAN Zheng-quan. Application of CAN bus in ship structure safety monitoring system[J]. Journal of electronic measurement and insturmentation, 2014, 28(5): 553-559.
[16] HU Yi-huai, HE Jian-hai, TANG Juan-juan, et al. Sail structure design and stability calculation for sail-assisted ships[J]. Marine Engineering Frontiers, 2015, 3: 1-13.
[17] SPARENBERG J A, WIERSMA A K. On the maximum thrust of sails by sailing close to wind[J]. Journal of ship research, 2017, 20(2): 98-106.
[18] 闫亚胜. 风能在现代船舶风翼助航中应用研究[J]. 海洋工程装备与技术, 2019(6): 389-393. YAN Ya-sheng. Research of wind energy using in modern sail-assisted vessel[J]. Ocean Engineering equipment and technology, 2019(6): 389-393.
[19] 江国和, 周中良, 胡以怀, 李涛涛, 曾向明. 基于ANSYS的船用风帆结构强度有限元模型分析[J]. 造船技术, 2011, (2): 10-12. JIANG Guo-he, ZHOU Zhong-liang, HU Yi-huai, et al. FEM structure analysis on strength of assisted-sail ship based on ANSYS[J]. Shipbuilding technology, 2011, (2): 10-12.
[20] 孔德仁, 朱蕴璞, 狄长安. 工程测试技术[M]. 北京: 科学出版社, 2003. KONG De-ren, ZHU Yun-pu, DI Chang-an. Engineering test technology[M]. Beijing: Science Press, 2003.
Study on the Measurement Method of Sail-assisted Thrust Based on Structural Strain Monitoring
YANG Hua-wei1,2, WANG Xue-liang1.2, ZHANG Tao1,2, CHEN Li3, XU Chun1,2, ZHENG Qing-xin1,2
(1. China Ship Scientific Research Center, Wuxi 214082, China; 2. Southern Marine Science and Engineering Guangdong Laboratory, Guangzhou 511458, China; 3. Dalian Shipbuilding Industry group design & research institute Co., Ltd., Dalian 116021, China)
This paper aims to propose a measurement method of sail thrust for real ship measurement. According to the requirement for thrust measurement of VLCC sail booster, the calculation formula of sail thrust and the mechanical state of the sail mast are analyzed, and then according to the strain measurement method of beam structure, the sail thrust measurement method and layout scheme of the measurement sensors based on the structural strain monitoring technology are proposed. The measurement method for sail thrust is verified by land-based load test. The results show that the structural strain difference of the measuring sensors increases with the sail thrust increasing, showing a significant linear relationship, and the linear correlation coefficient is 0.9965. The average error between the tested sail thrust and the actual trust is 5%. The proposed measurement method is feasible for real ship measurement.
sail booster; strain monitoring; sail thrust; measurement method; test thrust
2020-08-13;
2020-09-03
YANG Hua-wei (1981—), Male, Ph.D., Senior engineer, Research focus: structural health monitoring and assessment technology of ship hull.
杨华伟, 汪雪良, 张涛, 等. 基于结构应变监测的风帆推力测量方法研究[J]. 装备环境工程, 2021, 18(4): 109-114.
TN98
A
1672-9242(2021)04-0109-06
10.7643/ issn.1672-9242.2021.04.016
2020-08-13;
2020-09-03
南方海洋科学与工程广东省实验室(广州)人才团队引进重大专项(GML2019ZD0502)
Fund:Key Special Project for Introduced Talents Team of Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou) (GML2019ZD0502)
杨华伟(1981—),男,博士,高级工程师,主要研究方向为船舶结构健康监测及评估技术。
YANG Hua-wei, WANG Xue-liang, ZHANG Tao, et al. Study on the measurement method of sail-assisted thrust based on structural strain monitoring[J]. Equipment environmental engineering, 2021, 18(4): 109-114.
