基于改进D-S证据理论的滚抛磨块融合决策模型
2021-05-08范晓建田建艳杨英波菅垄杨胜强
范晓建,田建艳,杨英波,菅垄,杨胜强
基于改进D-S证据理论的滚抛磨块融合决策模型
范晓建a,田建艳a,杨英波b,菅垄a,杨胜强b
(太原理工大学 a.电气与动力工程学院 b.机械与运载工程学院,太原 030024)
为了能够有效利用滚磨光整加工数据库平台的案例知识和专家经验,提高新零件加工时滚抛磨块优选的准确率,解决不同优选方式优选结果的冲突问题。将案例推理、专家推理、迁移学习3种优选方式的滚抛磨块优选结果作为3种证据,根据3种优选方式计算的相似度结果构建滚抛磨块决策辨识框架,并采用合理的方法确定基本概率赋值。然后依据按冲突信息的比例分配基本概率赋值的方法对证据合成公式进行改进,避免传统的D-S证据理论在证据间高度冲突时出现融合结果有悖于实际情况的问题。接着采用改进的证据合成公式对3种证据进行融合决策。最后利用数据库平台中工厂加工实例数据进行仿真。基于数据库平台中已有的成功案例结果,通过仿真结果可以表明,该改进的融合决策模型可以解决不同优选方式优选结果之间的冲突问题,解决了原始合成公式的弊端问题,且融合决策结果较3种方法单独使用时具有更高的准确率,该融合决策模型的准确率达到88%。基于改进D-S证据理论的滚抛磨块融合决策模型,可以为滚磨光整加工时滚抛磨块的智能优选提供决策指导。
滚抛磨块;智能优选;融合决策;D-S证据理论;辨识框架;基本概率赋值
滚磨光整加工是先进制造中成形加工的组成部分,主要是通过滚抛磨块对零件表面进行碰撞、滚压、滑擦和刻划的微量磨削作用,提高零件表面质量,改善零件表面完整性[1-2]。国际权威机构统计认定,约有50%的机械零件采用该加工方法来提高表面质量[3]。随着零件质量要求的逐步提升,滚磨光整加工对传统制造业升级和高精度制造业发展起到了重要作用[4-5]。滚抛磨块作为主要的固体介质,对加工效果有着较大的影响。目前滚抛磨块种类较多,不同磨块的适用性不同,在实际加工中,主要根据现场专家的经验结合大量的试验进行优选,效率较低,且对于复杂零件缺乏有效的理论指导,因此有必要研究滚抛磨块智能优选方法。目前较为成熟的方法有基于案例推理(Case based reasoning,CBR)技术的滚抛磨块优选方法[6],通过计算待加工零件与案例库中每条案例的相似度,取相似度最高的案例所用磨块作为优选结果。但是对于相似度较低的零件,仅仅依据CBR技术优选结果可信度低,还需要结合专家经验以及新问题和历史案例之间的差异对滚抛磨块进行优选,为此课题组分别建立了基于专家推理(Expert reasoning,ER)和基于迁移学习(Transfer Learning,TL)的滚抛磨块优选模型[7-8]。针对同一个待加工零件,三者的优选结果之间可能会存在冲突问题,因此还需要合理解决冲突,对其进行融合决策,使得决策结果具有更高的可信度。
Dempster-Shafer(D-S)证据理论由Dempster在1967年提出,于1976 年由他的学生Shafer进一步发展完善。其作为一种有效的融合决策方法,可以为证据积累的过程提供证据合成方法,解决证据之间的冲突问题,得出各个假设的综合支持度[9]。目前,D-S证据理论已经在故障诊断、目标识别等融合决策领域得到了广泛的应用。袁杰等[10]提出一种基于D-S证据融合的混合专家系统故障诊断模型,针对不同环境下不同专家系统的可靠程度自适应分配权重,试验结果表明,对多种决策结果进行融合可以获得比单个决策更可靠的决策结果。Zhao Yi-bing等[11]为了使无人驾驶地面车辆在各种条件下进行障碍物识别,采用D-S证据理论对分别从摄像机和激光扫描仪中提取的障碍物特征证据进行融合,测试结果表明该方法在越野环境中具有较高的识别能力。Ma Wen-jun等[12]提出一种新的针对完全冲突情况的证据组合规则,避免融合结果出现与事实相反的情况,通过试验验证了该改进方法的优越性。上述学者从基本概率赋值的确定和合成规则的改进等方面进行了研究,较好地解决了各领域的融合决策问题,但大部分是针对一个问题的多特征融合,对多种决策结果进行融合的研究还较少。针对原始的D-S证据理论合成公式在证据之间高度冲突时存在的固有弊端问题,在D-S证据理论的改进方面,主要集中于将冲突部分的基本概率赋值分配给未知的焦元,此时完全忽略冲突信息。同时,由于根据证据之间的冲突大小给各证据分配权重,计算过程较复杂。本文在融合时将冲突部分基本概率赋值按比例分配给冲突的焦元,从而得到改进的证据合成公式。
为了充分利用案例信息、专家经验、差异信息等不同类型的知识,同时解决3种优选方式所得结果的冲突问题,得到准确的滚抛磨块决策结果。在课题组已经建立的基于CBR[13]、ER[14]、TL[8]3种滚抛磨块优选模型的基础上,将3种优选方式的优选结果作为3种证据,然后使用改进的D-S证据理论对3种证据进行融合,得出最终的决策结果。
1 基于改进D-S证据理论的滚抛磨块融合决策
基于CBR的优选旨在通过已有的相似案例对新问题的解决提供指导。基于ER的优选模拟专家思维进行滚抛磨块决策。基于TL的滚抛磨块优选考虑到新问题和历史案例之间的差异信息,通过缩小两者之间的分布差异,将历史案例的信息迁移到新问题的求解中,得到优选结果。因此,采用改进的D-S证据理论对3种优选结果进行融合,可以融合多种类型的知识。基于D-S证据理论的滚抛磨块融合决策技术路线如图1所示。
由图1可知,滚抛磨块的融合决策过程首先采用3种优选方式进行优选,然后根据优选结果构建滚抛磨块辨识框架并确定3种证据的基本概率赋值,最后采用改进的合成公式进行融合并给出融合决策结果。
1.1 滚抛磨块决策辨识框架的构建及基本概率赋值的确定
滚磨光整加工中产生的不同类型的知识,可以使用不同的方法加以利用,但是在使用过程中存在一定程度的不确定性。D-S证据理论通过建立滚抛磨块决策的辨识框架探讨证据的不确定性,通过基本概率赋值处理推理的不确定性,本节主要介绍根据3种优选方法中各滚抛磨块的相似度值构建辨识框架和确定基本概率赋值的方法。
1.1.1 滚抛磨块决策辨识框架的构建
定义1:在滚抛磨块决策时,所有可能用到的滚抛磨块用集合表示,且集合中的所有滚抛磨块两两互斥,决策结果只能取集合中的一种,则称此互不相容的滚抛磨块集合为辨识框架[15],可以表示为{1,2,···,B,···,B},B(=1,2,···,)为辨识框架中的一种滚抛磨块;是滚抛磨块的种类总数。
滚抛磨块决策的辨识框架包括所有可能用到的待选择滚抛磨块,由CBR、ER、TL中各滚抛磨块的相似度值动态确定,确定方法如下所述。
1)基于CBR的优选方式,通过计算新问题与案例库中案例之间的相似度进行案例检索,得出滚抛磨块。通常采用加权最近邻居法[16]进行计算,该方法在特定距离的定义下,使得距离最近的2个案例之间具有最高的相似度。计算公式如式(1)所示。
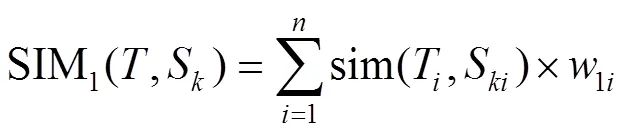
式中:表示待加工零件;S表示案例库中第个案例;T表示待加工零件的第个特征值;S表示案例库中第个案例的第个特征值;表示特征总数;SIM1(,S)表示新问题和案例库中第个案例的相似度;sim(T,S)表示两个案例的第个特征的相似度[6];1i表示根据实际加工需求赋予第个特征的主观权重[6]。
根据式(1)的计算结果,设定合理的相似度阈值SIM1th,取相似度值大于SIM1th的案例所用的滚抛磨块构成集合1。
2)在工厂实际加工过程中,专家通常依据零件尺寸、加工前表面状态及加工要求等选择滚抛磨块。故基于ER的优选方式中,首先按照专家的决策思维建立区间值模糊规则,将零件重要特征及加工要求隶属区间作为规则前件,所用磨块作为规则后件。推理时对待加工零件特征进行区间化描述,然后计算与规则库中每条规则的综合加权相似度作为规则匹配度,计算公式如式(2)所示。

式中:R表示规则库中第条规则;T表示待加工零件第个特征所对应的隶属区间;A表示规则库中第条规则的前件中第个特征的隶属区间;SIM2(,R)表示待加工零件与第条规则的综合加权相似度;sim(T,A)表示待加工零件与第条规则的第个特征的区间相似度[7];2i表示根据加工要求赋予第个特征的主观权重[7]。
根据式(2)计算结果,取相似度值大于阈值SIM2th的规则对应的规则后件即滚抛磨块构成集合2。
3)基于TL的优选方式为缩小新问题和历史案例数据的分布差异性,采用联合分布适配的方式求得变换矩阵,将两种数据投射到公共空间,在公共空间建立滚抛磨块优选模型,每个滚抛磨块采用4个参数进行描述,分别是磨块材质、磨块形状、磨块大小、磨块类型。采用TL得到滚抛磨块的4个特征参数后,通过计算4个特征参数所描述的磨块和磨块库中所有滚抛磨块的相似度,得到TL优选结果。计算公式如式(3)所示。

式中:T表示TL结果所描述的滚抛磨块;B表示磨块库中第个滚抛磨块;T表示TL结果所描述的滚抛磨块的第(=1,2,3,4)个特征值;B表示第个滚抛磨块的第个特征值;SIM3(T,B)表示TL结果所描述的滚抛磨块和磨块库中第个滚抛磨块的相似度;sim(T,B)表示第个滚抛磨块特征的相似度[8];3i表示第个滚抛磨块特征的权重[8]。
根据式(3)的计算结果,取相似度值大于阈值SIM3th的滚抛磨块构成集合3。最后取三者的并集完成滚抛磨块决策辨识框架的构建,即:1∪2∪3。
1.1.2 3种证据基本概率赋值的确定

基本概率赋值表示3种证据对辨识框架中各个磨块的支持程度,依据各种优选方式的相似度结果进行确定,CBR、ER、TL的基本概率赋值分别用1、2、3表示。由于篇幅所限,本文以CBR为例阐述基本概率赋值1的确定方法,其他两种方式的基本概率赋值2、3的确定方法基本相似。
首先判断B1∩是否成立,若不成立,1(B)=0;若成立,1(B)具体的赋值方法流程图如图2所示。
图2中,SIM1(T,B)=1(,S),其中B为案例S所用的磨块;MF=MS–,其中参数是一个很小的正数,通常取0.01~0.05;1表示集合中案例的个数;1、2为根据相似度值及MF值将滚抛磨块划分所得的2个集合,即:1为相似度值大于等于MF的案例所用的滚抛磨块构成的集合,2为其余案例所用的滚抛磨块构成的集合。

图2 CBR的基本概率赋值确定流程图
1.2 D-S证据理论合成公式的改进


式中:为冲突系数,表示两种优选方式优选结果的冲突大小,∈[0,1]。同理可得的计算公式。
对于公式(4),当=1时,证据完全冲突,公式失效[22-23];当接近于1时,证据之间高度冲突,可能导致融合结果与事实相悖[24-25]。为避免融合过程中出现这两种问题,提出将冲突部分基本概率赋值按比例分配给冲突的磨块,在2个证据融合的情形下,需要满足如式(5)所示的条件。

由式(5)可解得:

由此得到如式(7)所示的D-S证据理论合成公式:

由式(7)可知,改进后的合成公式中,既包括两证据不冲突信息部分,又包括冲突信息部分,所以在对融合后的焦元分配基本概率赋值时,没有将冲突信息盲目的全盘否定,从而可以提高合成结果的可靠性。
1.3 滚抛磨块融合决策步骤
基于改进D-S证据理论的滚抛磨块融合决策步骤如下所示。
Step 1 分别采用CBR、ER、TL进行磨块优选,通过公式(1)—(3)分别得到3种优选方式中各滚抛磨块所对应的相似度值。
Step 2 根据Step 1中结果分别得到滚抛磨块集合1、2、3,然后构造滚抛磨块决策辨识框架1∪2∪3。
Step 3 根据图2中的流程确定CBR的基本概率赋值1,并采用类似的方法确定ER和TL的基本概率赋值2、3。
Step 4 对3种证据进行融合:首先采用公式(7)对其中两种证据进行合成,然后将所得合成结果与第3种证据再次进行合成,得到最终的各滚抛磨块的基本概率赋值。
Step 5 取融合后基本概率赋值最大值对应的滚抛磨块作为最终的决策结果。
2 试验仿真与结果分析
2.1 数据来源
在滚磨光整加工中,滚抛磨块按照加工类型可分为粗磨、中磨、精磨、超精磨等,加工设备有主轴式(旋流式)、离心式、涡流式、振动式等。采用工厂的100个轴类零件加工案例数据作为测试数据进行仿真,由于篇幅所限,仅列举曲轴类零件的仿真结果,其加工方式以主轴式(旋流式)设备居多,曲轴类零件、加工设备、滚抛磨块的简单图示如图3所示。
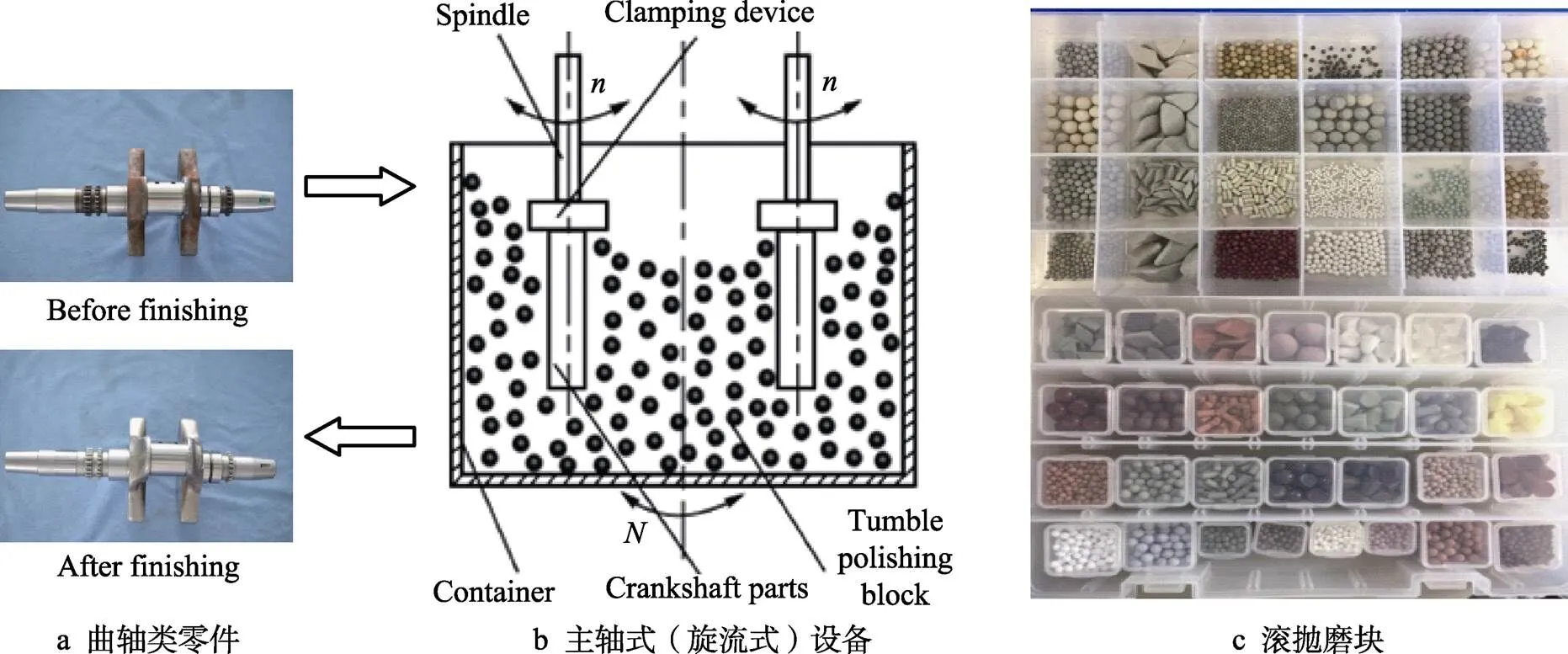
图3 曲轴类零件、加工设备及滚抛磨块的图示
2.2 参数确定
在构造辨识框架的过程中,对于不同类型的零件,有不同的最佳相似度阈值。针对曲轴类案例的相似度阈值设定问题进行了大量仿真,不同的相似度阈值对应的融合决策准确率结果如图4所示。

图4 融合决策准确率随相似度阈值的变化曲线
图4中,决策准确率(Decision accuracy,Acc)的计算公式如式(8)所示。
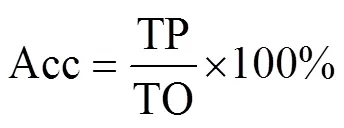
式中:TP为决策结果和案例实际所用磨块相同的案例数;TO为参与仿真的案例总数。
由图4可知,相似度阈值会影响决策的准确率,当相似度阈值为0.77~0.85时,具有最高的决策准确率(92%)。因为较高相似度阈值会丢失辨识框架中正确的滚抛磨块,而较低的相似度阈值会使辨识框架中纳入过多错误的滚抛磨块,均会使融合决策的准确率降低。因此,在保证决策准确率的同时,为降低算法的时间和空间复杂度,本文选择相似度阈值为0.85。
对于不同优选方式以及不同待加工零件的优选结果,应该合理地选择参数,以使各自的基本概率赋值更具合理性。首先根据模型要求以及优选方式确定大致范围,然后根据仿真结果进行适当调整,当3种优选方式的参数的取值分别为0.02、0.02、0.03时,融合决策的准确率最高,说明此时参数设定最合理。
2.3 实际案例仿真
分别采用CBR、ER、TL3种方法进行优选,每种方法取该方法所对应的基本概率赋值最大的滚抛磨块作为优选结果,3种方法优选结果的正确数量能一定程度反应三者之间的冲突大小。因此,按照3种方法优选结果的正确数量,分3种情况列举曲轴类案例的融合决策仿真结果。其中每条测试案例由11个案例特征及所用滚抛磨块组成,11个案例特征1—11分别代表本文所举例的待加工曲轴类零件的长度、轴径、加工前粗糙度、加工前毛刺、加工前光亮度、加工前硬度、加工后粗糙度、加工后毛刺、加工后光亮度、加工后硬度、残余应力改善。5、9按国家标准分为:可辨加工痕迹方向、无光亮度、较低且没有磨纹、光亮度非常高4种等级[13],分别赋值为1、2、3、4。8表示加工后毛刺是否存在,若为0,表示加工后毛刺还存在;若为1,表示加工后毛刺被去除。
2.3.1 其中两种方法的结果正确
3种方法的优选结果中仅有两种方法的结果正确时,各种方法所得的优选及融合决策结果如表1所示。
表1 仅有两种方法的优选结果正确时的各方法结果

Tab.1 Results of each method when only have two methods’ results are correct in the three methods
2.3.2 仅有一种方法的结果正确
当3种方法的优选结果中仅有一种方法的结果正确时,各种方法所得的优选及融合决策结果如表2所示。
由表2可知,采用本文所提改进方法融合后,No.9、10、12、13正确,原始合成公式融合后有No.11可以得到决策结果,但错误。根据公式(4)中冲突值的计算方法,表2中案例平均冲突值较表1中有所增大。采用原始的D-S证据理论融合准确率有所降低,而采用改进的D-S证据理论进行融合同样可以获得较3种方法更准确的结果。
2.3.3 3种方法的结果都错误
当3种方法的优选结果都错误时,各种方法所得的优选及融合决策结果如表3所示。
表2 仅有一种方法的优选结果正确时的各方法结果

Tab.2 Results of each method when only have one method’s result is correct in the three methods
表3 3种方法的优选结果都错误时的各方法结果

Tab.3 Results of each method when the optimization results of the three methods are wrong
由表3可知,采用本文所提改进方法融合后,No.15、17、18、19正确,而原始的合成方法均未能得出结果。根据公式(4)中冲突值的计算方法,此时各案例均为完全冲突。由此可知,随着冲突值的逐渐增大,原始的D-S证据理论融合效果逐渐变差,而采用改进的D-S证据理论进行融合均可以获得较3种方法更准确的结果。
对100个测试数据的仿真结果进行统计,其中采用改进的合成公式融合后,准确率达到88%,而采用未改进的合成公式进行融合,由于证据之间存在较大冲突,准确率仅为43%。因此,基于改进D-S证据理论的融合决策能通过合理分配冲突信息使其得到有效解决,并得出更准确的决策结果。
3 结论
1)针对同一个待加工零件,若采用CBR、ER、TL3种优选方式优选的滚抛磨块结论一致,则可直接采用。若3种优选方式的优选结果冲突,有必要采用D-S证据理论融合方法。
2)当冲突较大或完全冲突时,采用原始的D-S证据理论合成公式的融合结果也会出现有悖于实际的情况,甚至不能得出融合结果。这说明改进D-S证据理论十分必要。
3)采用本文提出的改进D-S证据理论融合决策模型,能有效地解决3种不同优选方式结果的冲突问题,通过融合相关知识,可使融合结果较3种方法单独优选具有更高的可信度,可以为实际加工提供有效的工艺指导。
[1] YANG Sheng-qiang, LI Wen-hui. Surface finishing theory and new technology[M]. Berlin: Springer Press, 2018.
[2] 杨胜强, 李文辉, 李秀红, 等. 高性能零件滚磨光整加工的研究进展[J]. 表面技术, 2019, 48(10): 13-24. YANG Sheng-qiang, LI Wen-hui, LI Xiu-hong, et al. Research development of mass finishing for high-performance parts[J]. Surface technology, 2019, 48(10): 13-24.
[3] CARIAPA V, PARK H, KIM J, et al. Development of a metal removal model using spherical ceramic media in a centrifugal disk mass finishing machine[J]. The international journal of advanced manufacturing technology, 2008, 39(1): 92-106.
[4] 杨胜强, 王秀枝, 李文辉. 振动式滚磨光整加工技术的研究现状及再发展[J]. 太原理工大学学报, 2017, 48(3): 385-392. YANG Sheng-qiang, WANG Xiu-zhi, LI Wen-hui. Research status and future development of vibratory finishing technology[J]. Journal of Taiyuan University of Technology, 2017, 48(3): 385-392.
[5] 赵光辉. 齿面各向同性光整工艺对齿面接触疲劳特性影响的研究[D]. 北京: 机械科学研究总院, 2017. ZHAO Guang-hui. Study on influence of isotropic finishing process on contact fatigue characteristics of tooth surface[D]. Beijing: China Academy of Machinery Science and Technology, 2017.
[6] 杨炎, 高炜, 杨胜强, 等. 基于模糊聚类和案例推理的滚抛磨块优选模型[J]. 表面技术, 2019, 48(9): 315-320. YANG Yan, GAO Wei, YANG Sheng-qiang, et al. Optimal model of the abrasive blocks based on fuzzy clustering and case-based reasoning[J]. Surface technology, 2019, 48(9): 315-320.
[7] 周鑫焱, 田建艳, 高炜, 等. 基于专家推理的滚抛磨块优选模型研究[J]. 现代制造工程, 2020(6): 98-103. ZHOU Xin-yan, TIAN Jian-yan, GAO Wei, et al. Research on optimal model of the abrasive blocks based on expert reasoning[J]. Modern manufacturing engineering, 2020(6): 98-103.
[8] 闫瑞斌. 基于迁移学习的滚抛磨块优选模型研究[D]. 太原: 太原理工大学, 2020. YAN Rui-bin. Research on optimal model of the abrasive media based on transfer learning[D]. Taiyuan: Taiyuan University of Technology, 2020.
[9] 孙子文, 李松, 孙晓雯. 基于D-S证据理论的人体跌倒检测方法[J]. 计算机工程与科学, 2018, 40(5): 829-835. SUN Zi-wen, LI Song, SUN Xiao-wen. A human fall detection method based on D-S evidence theory[J]. Computer engineering & science, 2018, 40(5): 829-835.
[10] 袁杰, 王福利, 王姝, 等. 基于D-S融合的混合专家知识系统故障诊断方法[J]. 自动化学报, 2017, 43(9): 1580-1587. YUAN Jie, WANG Fu-li, WANG Shu, et al. A fault diagnosis approach by D-S fusion theory and hybrid expert knowledge system[J]. Acta automatica sinica, 2017, 43(9): 1580-1587.
[11] ZHAO Yi-bing, DING Feng, LI Ji-ning, et al. The intelligent obstacle sensing and recognizing method based on D-S evidence theory for UGV[J]. Future generation computer systems, 2019, 97: 21-29.
[12] MA Wen-jun, JIANG Yun-cheng, LUO Xu-dong. A flexible rule for evidential combination in Dempster-Shafer theory of evidence[J]. Applied soft computing journal, 2019, 85: 105512.
[13] 杨炎. 基于模糊聚类和案例推理的滚抛磨块优选模型研究[D]. 太原: 太原理工大学, 2019. YANG Yan. Research on optimal model of the abrasive blocks based on fuzzy clustering and case-based reasoning[D]. Taiyuan: Taiyuan University of Technology, 2019.
[14] 周鑫焱. 基于专家系统的滚抛磨块优选模型研究[D]. 太原: 太原理工大学, 2020. ZHOU Xin-yan. Research on optimal model of the abrasive media based on expert system[D]. Taiyuan: Taiyuan University of Technology, 2020.
[15] XU Hong-hui, DENG Yong. Dependent evidence combination based on decision-making trial and evaluation laboratory method[J]. International journal of intelligent systems, 2019, 34(7): 1555-1571.
[16] KHOSRAVANI M R, NASIRI S, WEINBERG K. Application of case-based reasoning in a fault detection system for injection molding process of drippers[J]. Applied soft computing journal, 2019, 75: 227-232.
[17] MA Wen-jun, LIU We-ru, LUO Xu-dong, et al. A Dempster-Shafer theory and uninorm-based framework of reasoning and multiattribute decision-making for surveillance system[J]. International journal of intelligent systems, 2019, 34(11): 3077-3104.
[18] 魏东. D-S证据理论合成规则的改进及其应用[D]. 北京: 北京工业大学, 2018.WEI Dong. The improvement and application of Dempster-Shafer rule of combination[D]. Beijing: Beijing University of Technology, 2018.
[19] DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. The annals of mathematical statistics, 1967, 38(2): 325-339.
[20] WANG Hui, GUO Li-li, DOU Zheng, et al. A new method of cognitive signal recognition based on hybrid information entropy and D-S evidence theory[J]. Mobile networks and applications, 2018, 23(4): 677-685.
[21] YANG Hao, HASSAN S G, WANG Liang, et al. Fault diagnosis method for water quality monitoring and control equipment in aquaculture based on multiple SVM combined with D-S evidence theory[J]. Computers & electronics in agriculture, 2017, 141: 96-108.
[22] XIAO Fu-yuan. A new divergence measure for belief functions in D-S evidence theory for multisensor data fusion[J]. Information sciences, 2020, 514: 462-483.
[23] SHI Wen-zao, MAO Zheng-yuan. Automatic detection of urban area from the remote sensing imagery based on improved D-S evidence theory[J]. The imaging science journal, 2017, 65(5): 261-269.
[24] TANG Xiang-hong, GU Xin, WANG Jia-chen, et al.A bearing fault diagnosis method based on feature selection feedback network and improved D-S evidence fusion[J]. IEEE access, 2020, 8: 20523-20536.
[25] ZHAO Qian-yu, WANG Shou-xiang, WANG Kai, et al. Multi-objective optimal allocation of distributed generations under uncertainty based on D-S evidence theory and affine arithmetic[J]. International journal of electrical power and energy systems, 2019, 112: 70-82.
Fusion Decision Model of Tumbling Chip Abrasives Based on Improved D-S Evidence Theory
-a,-a,-b,a,-b
(a.School of Electrical and Power Engineering, b.School of Mechanical and Vehicle Engineering, Taiyuan University of Technology, Taiyuan 030024, China)
As the primary solid medium in the barrel finishing process, the tumbling chip abrasives has a great influence on the processing effect. In order to effectively utilize the case knowledge and expert experience of the database of barrel finishing process, and improve the accuracy of the optimization of tumbling chip abrasives when the new part are processed, the research group have established the optimization model of tumbling chip abrasives based on case-based reasoning, expert reasoning and transfer learning respectively. However, optimization result only based on three independent methods had low reliability,for the new part to be processed, there will be conflicts among the three optimization results, so that it is necessary to make a fusion decision for the three optimization results. Therefore, a fusion decision model of tumbling chip abrasives based on improved D-S evidence theory is proposed. Firstly, the optimization results of case-based reasoning, expert reasoning and transfer learning are used as three kinds of evidence. According to the similarity results calculated by the three optimization methods, the decision frame of discernment of tumbling chip abrasives is constructed, and a reasonable method is used to determine the basic probability assignment. Secondly, aiming at the problem that the fusion results are contrary to the actual situation when the evidences are highly conflicting in the traditional D-S evidence theory, the method of distributing the basic probability assignment according to the proportion of conflict information is used to improve the synthesize formula. Then, the improved synthesize formula is used to fuse the three kinds of evidence. Finally, the simulation is carried out by using the real data of factory processing in the database. Based on existing case results, a large number of simulation results show that the improved fusion decision model can solve the conflicts between the optimization results of different optimization methods as well as the disadvantages of the original synthesis formula. The results of fusion decision have higher accuracy than those of the other three methods. The accuracy of the fusion decision model reaches 88%, which shows that the proposed decision model can provide decision guidance for intelligent optimization of tumbling chip abrasives.
tumbling chip abrasives; intelligent optimization; fusion decision; D-S evidence theory; frame of discernment; basic probability assignment
2020-08-10;
2020-11-24
FAN Xiao-jian (1996—), Male, Master, Research focus: complex system modeling and intelligent control.
田建艳(1966—),女,博士,教授,主要研究方向为复杂系统建模与智能监控系统研究。邮箱:tut_tianjy@163.com
Corresponding author:TIAN Jian-yan (1966—), Female, Doctor, Professor, Research focus: research on complex system modeling and intelligent monitoring system. E-mail: tut_tianjy@163.com
范晓建, 田建艳, 杨英波, 等. 基于改进D-S证据理论的滚抛磨块融合决策模型[J]. 表面技术, 2021, 50(4): 393-401.
TG356.28
A
1001-3660(2021)04-0393-09
10.16490/j.cnki.issn.1001-3660.2021.04.042
2020-08-10;
2020-11-24
山西省重点研发计划项目(201903D121057);山西省回国留学人员科研资助项目(2017-032);山西省自然科学基金重点项目(201801D111002)
Fund:Supported by the Key Research and Development (R&D) Projects of Shanxi Province of China (201903D121057); Research Project Supported by the Shanxi Scholarship Council of China (2017-032) and the Key Project of Natural Science Foundation of Shanxi Province of China (201801D111002)
范晓建(1996—),男,硕士研究生,研究方向为复杂系统建模与智能控制。
FAN Xiao-jian, TIAN Jian-yan, YANG Ying-bo, et al. Fusion decision model of tumbling chip abrasives based on improved D-S evidence theory[J]. Surface technology, 2021, 50(4): 393-401.
