基于IFA-BPNN的长输管道外腐蚀速率预测
2021-05-08凌晓徐鲁帅高甲程马娟娟马贺清付小华
凌晓,徐鲁帅,高甲程,马娟娟,马贺清,付小华
基于IFA-BPNN的长输管道外腐蚀速率预测
凌晓1a,徐鲁帅1a,高甲程2,马娟娟1a,马贺清1a,付小华1b
(1.兰州理工大学 a.石油化工学院 b.理学院,兰州 730050;2.中国石油天然气股份有限公司 甘肃兰州销售分公司,兰州 730050)
构建陆地长输管道外腐蚀速率的预测模型,提升管道外腐蚀速率预测的精度,对长输管道外腐蚀状态进行准确把控。深入解析了萤火虫算法(FA)的工作原理,针对FA易出现陷入局部最优或因控制参数设置不合适而导致函数无法收敛等问题,提出了FA的改进方案:采用Logistics混沌映射的方法初始化萤火虫的位置,提升萤火虫种群的所养性;引入一种新的惯性权重计算方法来改进萤火虫位置移动公式,提升FA全局寻优能力。利用改进的萤火虫算法(IFA)对误差反向传播神经网络(BPNN)初始权值和阈值进行优化,建立基于IFA-BPNN的长输管道外腐蚀速率预测模型。以111组长输管道外腐蚀检测数据为例,在MATLAB中进行模拟仿真计算,使用粒子群算法优化的BPNN(PSO-BPNN)、遗传算法优化的BPNN(GA-BPNN)以及未进行优化的BPNN作为对比模型进行对比分析。使用IFA优化BPNN,大幅提升了BPNN模型的预测精度。使用IFA-BPNN模型预测12组管道腐蚀速率,平均相对误差仅为5.94%,预测结果的2为0.995 95,均优于BPNN、PSO-BPNN以及GA-BPNN模型的预测结果。IFA-BPNN作为预测管道腐蚀速率工具具有较好的预测精度和鲁棒性。
萤火虫算法;BP神经网络;混沌初始化;惯性权重;管道;腐蚀速率预测
管道作为最快速、最安全的石油和天然气运输方式,建设规模不断扩大。2019年末,我国长输管道总里程已达13.9×104km[1],管道失效将直接影响企业的经济效益和居民的安全[2-3]。近年来,国内外研究人员对管道失效模式进行了大量研究,发现腐蚀是造成油气长输管道失效的主要原因之一[4-6]。管道开挖检测费时费力,易造成资源浪费。因此,基于算法模型以及影响管道腐蚀的各项数据,对管道腐蚀状态进行准确预测,可为管道检维修提供决策支持,对保障管道安全运行具有重大意义[7-11]。
张河苇等[12]使用互信息理论确定了管道腐蚀的主要影响因素,为选取预测管道腐蚀速率的数据提供了决策支持。毕傲睿等[13]利用主成分分析法对输油管道内腐蚀因素进行优选,选出了影响管道腐蚀的主要因素,并结合改进的支持向量机模型对管道内腐蚀情况进行预测,且结果较为理想,但支持向量机由于算法本体缺陷,针对大规模训练样本难以实施。陈迪等[14]研究发现了影响含硫管道腐蚀情况的四大因素,并结合实验结论建立了一套预测含硫管道腐蚀状态模型,预测效果较优,但该模型仅针对管道内腐蚀有效,不适用于管道外腐蚀速率预测。章玉婷等[15]使用单一的BP神经网络(BP Neural Network,BPNN)对管道腐蚀速率进行分析预测,由于未经优化的BPNN易陷入局部最优,因此预测值相对真实数据误差较大。董绍华等提出中国管道的发展目标是建立基于管道全生命周期大数据的智慧管网[16],而基于机器学习的管道大数据分析处理是构建智慧管网的重要内容之一。近年来,Yang等[17-19]提出了萤火虫算法(Firefly Algorithm,FA),并通过仿真证实了FA要优于粒子群优化算法(Particle Swarm Optimization,PSO)和遗传算法(Genetic Algorithm,GA)。NANDY等[20]使用FA优化BPNN的初始权值和阈值,并通过仿真证实了其可行性。
综上所述,目前研究工作着重于管道腐蚀小样本数据预测研究,或因算法本体缺陷而导致腐蚀速率的预测误差较大。随着智慧管网的发展,管道数据采集量将会增大,而BPNN可应对数据量较大的问题。因此,本文对FA算法进行了改进,增强其全局寻优能力,并利用IFA对BPNN初始权值和阈值进行优化,建立了基于IFA-BPNN的长输管道外腐蚀速率预测模型,并对该模型进行实例应用,验证了该模型的适应性和鲁棒性。
1 BPNN及其优化模型介绍
BPNN模型具有较强的非线性函数拟合能力,但该模型常因初始权值和阈值的设置不当而陷入局部最优,从而使模型预测结果不理想。为改进BPNN本体存在的不足,本文提出使用IFA对BPNN初始值进行优化,并以GA和PSO作为对比优化模型进行测试分析,以验证IFA-BPNN模型的使用效果。
1.1 BPNN模型概述
BPNN于1986年提出,是现阶段应用较广泛的神经网络模型之一。BPNN一般采用3层网络结构便可达到良好的非线性逼近效果[21-22]。BPNN输入和输出的节点数量分别根据数据输入类别和预期输出类别确定,隐藏层中的节点数量可根据经验公式确定,各层通过权值相连,隐藏层和输出层各节点设有阈值。BPNN网络拓扑图如图1所示。
BPNN模型正向传递过程按式(1)—(4)进行运算[9]。
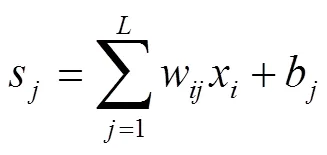

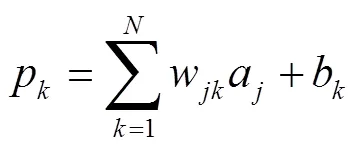
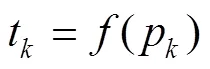

图1 BPNN模型示意图
误差反向传播的误差函数公式及权值阈值修正系数的公式为[9]:



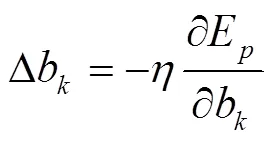

1.2 GA模型
GA由Holland及其学生于1975年创建,其思想是基于达尔文的进化论和Mendel的遗传学说,其主体分为选择、交叉和变异三部分[23-24]:
1)选择。文内采用轮盘赌方法进行选择操作,其公式为式(10),其中f计算公式与式(5)相同。

2)交叉。文中采用实数交叉法,公式见式(11)。

3)变异。变异操作的公式见式(12)。
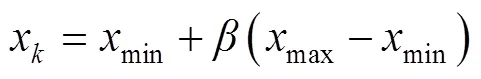
1.3 PSO模型
PSO算法原理是随机初始化一组粒子,通过跟踪个体极值和群体极值来更新粒子群,粒子的速度和位置分别根据式(13)和式(14)更新[25]。
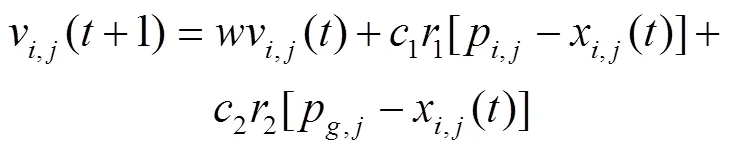

惯性权重采用线性递减的方式[26],其计算公式见式(15)。

1.4 FA模型及改进
1.4.1 FA模型






4)计算更新位置后萤火虫的亮度。
5)满足结束条件后输出全局极值和最优个体值;若不满足,转步骤2继续迭代搜索,迭代次数加1。
1.4.2 FA模型改进策略
FA作为新型优化算法,易出现陷入局部最优或因控制参数设置不合适而导致函数无法收敛等问题[27-29]。鉴于上述问题,对FA进行改进,表1为IFA的伪代码。
表1 IFA伪代码

Tab.1 IFA pseudocode
处理流程如下所述。
1)对萤火虫位置进行Logistics混沌初始化,提升了萤火虫初始种群的多样性和萤火虫搜索的全局遍历性,又与萤火虫随机初始化位置本质相匹配。Logistics混沌映射公式见式(20)[30]。
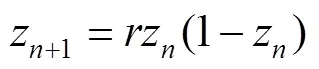



2 管道外腐蚀速率预测模型构建
分别使用GA、PSO以及IFA 3种优化算法对BPNN的初始权值和阈值进行优化,结合第1节各算法的理论基础,构建长输管道外腐蚀速率预测模型GA-BPNN、PSO-BPNN和IFA-BPNN,具体的模型构建流程如图2所示。
3 模型评价指标



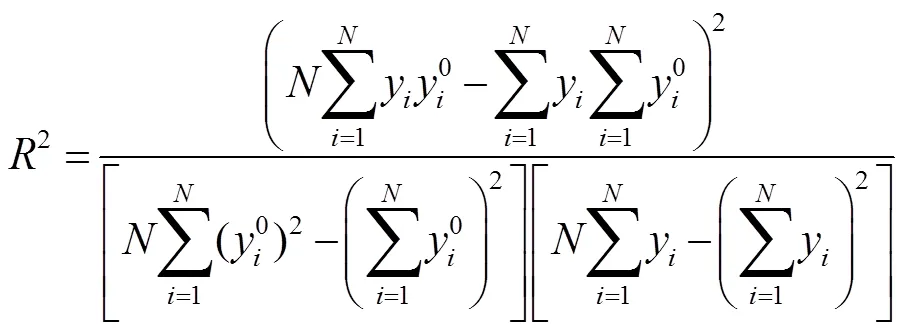
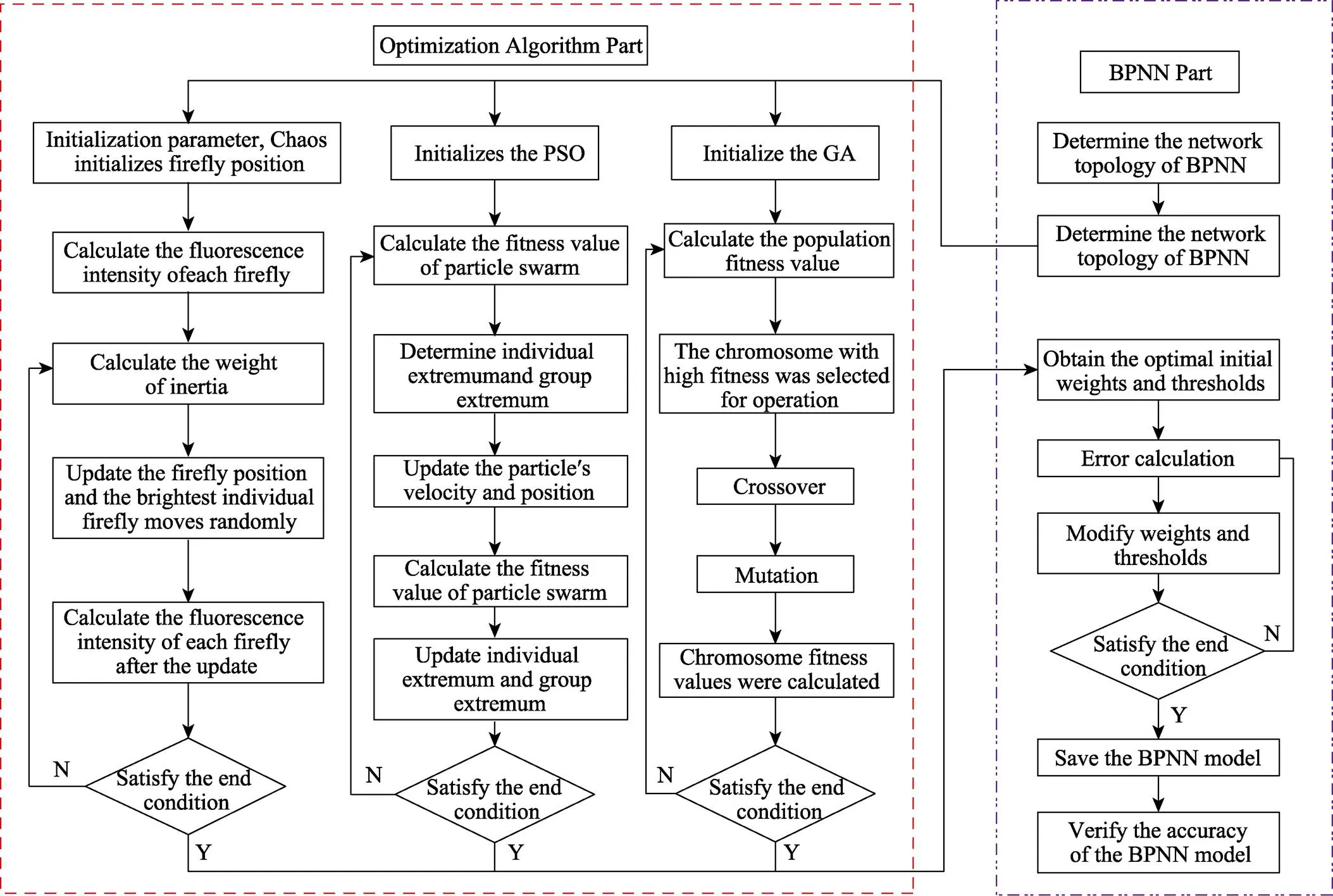
图2 混合模型流程图
4 实例分析
4.1 数据采集
选用文献[32]的111组管道外腐蚀数据,这111组数据的管道防腐层均为煤焦油瓷漆涂层。因数据组数较多,文内仅展示20组检测数据,如表2所示。每组数据包含11项检测数据,其中Corrosion rate为管道外腐蚀速率,TT为管道运行总时长,PP为氧化还原电位,pH为管道外界土壤的pH值,RP为管地电位,RE为土壤电阻率。此数据集包括对现场开挖点的土壤成分分析数据,该数据集采用标准实验室方法进行分析检测,所测数据类型包括含水量(WC)、容重(BD)及溶解氯化物(CC)、碳酸氢盐(BC)、硫酸盐(SC)的离子浓度。随机选取99组数据让各模型进行学习训练,利用剩余的12组数据对各模型进行测试分析。
4.2 模型参数设置
分别使用未经优化的BPNN模型、GA-BPNN模型、PSO-BPNN模型、IFA-BPNN模型进行管道数据的学习预测。
4.2.1 BPNN网络设置
BPNN采用3层网络结构,各层节点数的设置方法如下所述。
BPNN输入数据类型包括管道运行总时长,氧化还原电位,管道外界土壤的pH值,管地电位,土壤电阻率,土壤含水量,容重,土壤中溶解氯化物、碳酸氢盐以及硫酸盐离子浓度。BPNN输出数据为管道外腐蚀速率。因此,将BPNN输入层节点数设为10,输出层节点数设为1。隐含层神经元节点数根据经验公式(27)计算选取[33],因为log2(99)≈7,所以BPNN隐含层神经元节点数设置为7。

隐含层选用logsig函数作为传递函数,其表达式见式(28)。选用pureline型函数作为输出层的传递函数,表达式见式(29)。
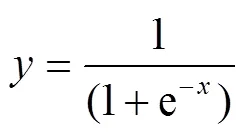

4.2.2 模型初始化设置

表2 长输管道外腐蚀数据集
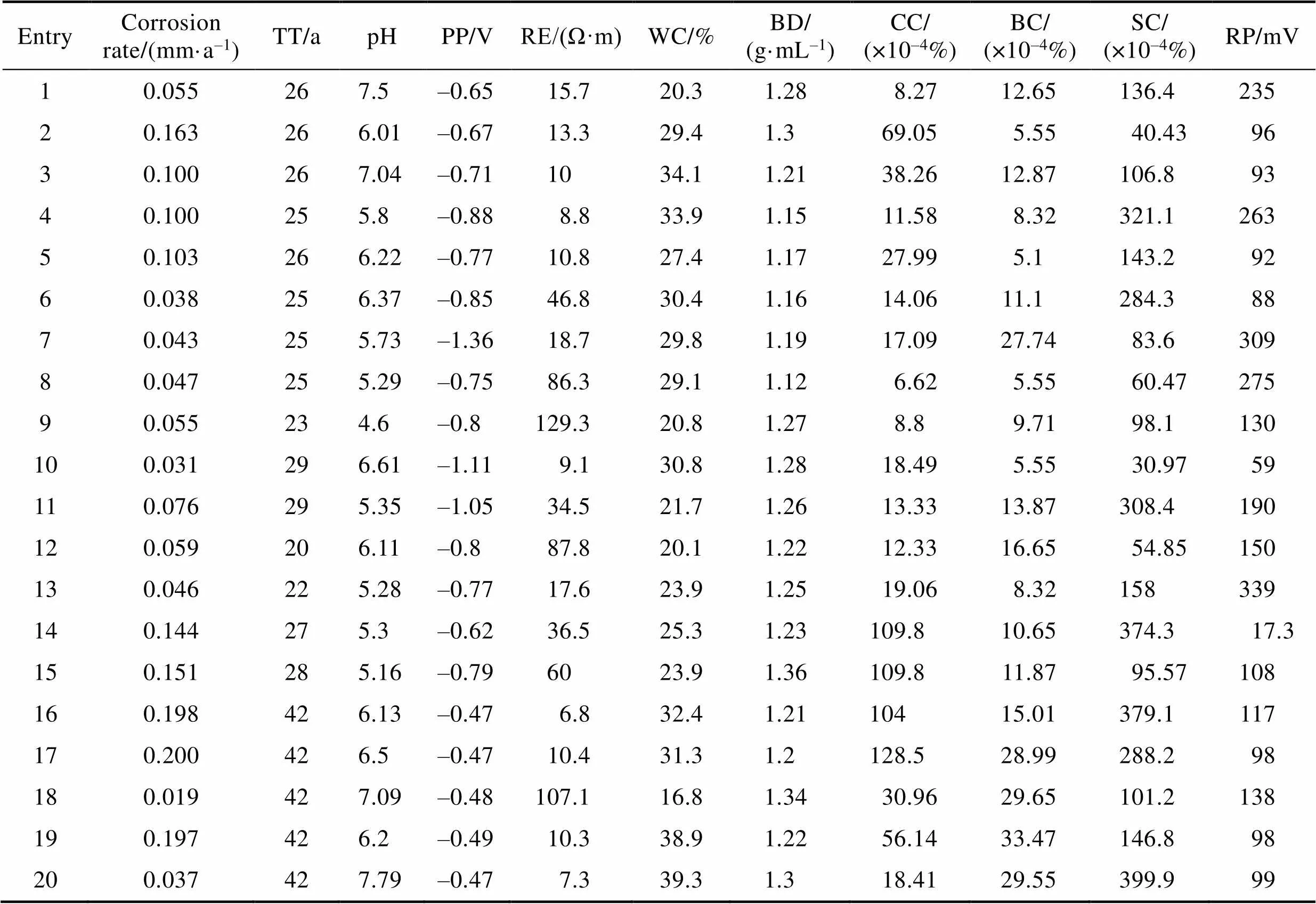
Tab.2 External corrosion data set of long-distance pipeline
表3 GA初始化参数
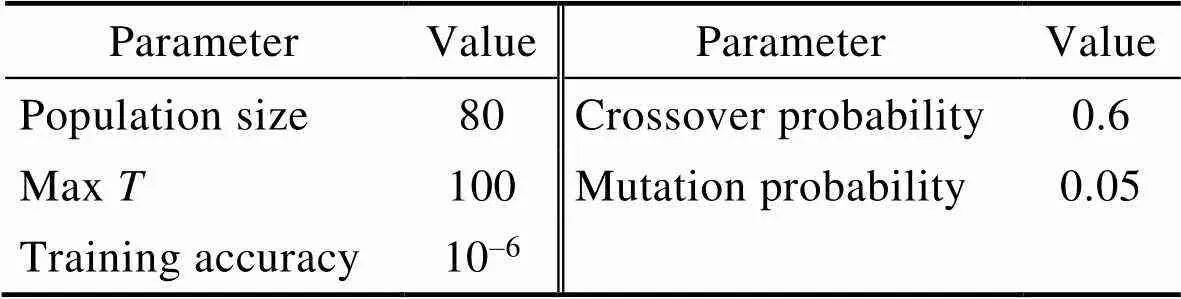
Tab.3 GA initialization parameters
表4 PSO初始化参数

Tab.4 PSO initialization parameters
表5 IFA初始化参数

Tab.5 IFA initialization parameters
5 结果分析
为避免数值问题,加快BPNN的收敛速度,在进行训练之前,对所有数据进行归一化操作,归一化公式见式(30)。

模型训练后的测试结果如表6、图3和图4所示。由表6可知,使用未经优化的BPNN预测管道腐蚀速率的效果最差,最大相对误差(Max RE)达到了30.88%,最小相对误差(Min RE)为14.17%;预测效果最好的是IFA-BPNN模型,其预测结果的Max RE为8.82%,Min RE仅为1.47%,也就是其误差区间为[1.47%,8.82%];相较于PSO-BPNN和GA-BPNN模型的误差区间,IFA-BPNN模型的[Min RE,Max RE]的取值最小,跨度最小,证明了IFA-BPNN的预测精度要优于BPNN、PSO-BPNN以及GA-BPNN。为进一步分析验证IFA-BPNN的使用效果,对BPNN、PSO-BPNN、GA-BPNN、IFA-BPNN的预测结果进行MAE计算,结果分别为22.26%、15.03%、10.74%、5.94%。相较于BPNN、PSO-BPNN、GA-BPNN预测结果的平均相对误差,IFA-BPNN分别提升了16.32%、9.09%、4.8%。使用训练好的模型BPNN、PSO-BPNN、GA-BPNN、IFA-BPNN对训练集的99组数据进行测试,其平均相对误差分别为18.11%、12.54%、9.12%、5.66%,进一步验证了利用IFA优化BPNN后可有效提升其预测精度。
表6 模型预测误差统计表
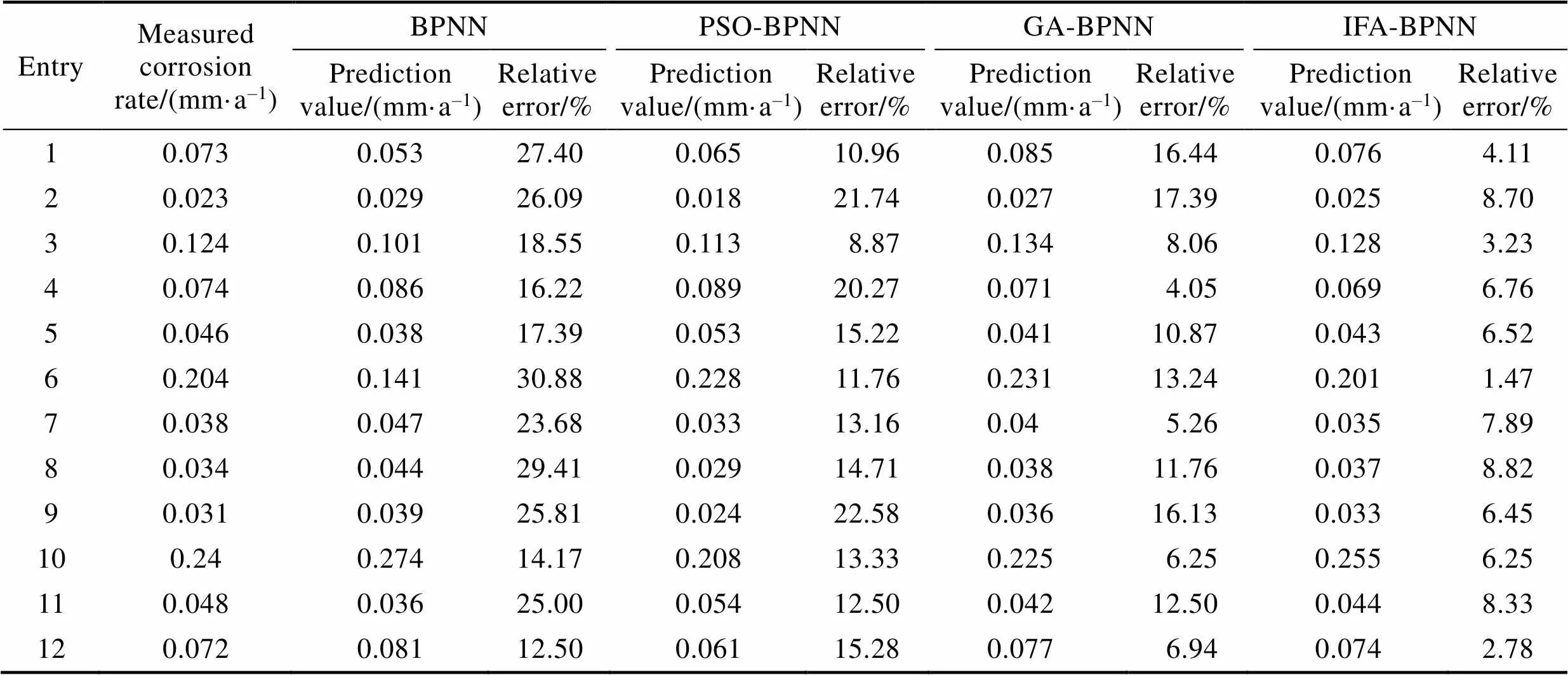
Tab.6 Model prediction error statistics table

图3 模型预测结果对比图

图4 模型预测误差曲线图
由图3可见,IFA-BPNN预测的管道外腐蚀速率与实测值最接近,相较于未经优化的BPNN,其预测精度有了较大幅度的提升,且IFA-BPNN的预测精度也优于PSO-BPNN和GA-BPNN。图4为预测结果的误差对比图。由图4可见,BPNN预测结果的误差最大,PSO-BPNN次之,GA-BPNN优于BPNN和PSO-BPNN,IFA-BPNN预测结果的相对误差最小,且相对误差曲线最为平缓,这不仅体现出IFA-BPNN模型预测结果的准确率较高,也体现出该模型具有较强的鲁棒性。
分别把BPNN、PSO-BPNN、GA-BPNN、IFA-BPNN预测的管道腐蚀速率与实际检测的管道外腐蚀速率进行相关性分析,其结果如图5—8所示,图中黑色线公式为=,红色线为预测结果拟合线。可知BPNN模型的2为0.88037,PSO-BPNN的2为0.95876,GA-BPNN的2为0.97888,IFA-BPNN的2为0.99595。IFA-BPNN的2最接近1,这进一步验证了IFA-BPNN作为预测管道腐蚀速率工具的准确性和鲁棒性。

图5 BPNN预测结果线性拟合图

图6 PSO-BPNN预测结果线性拟合图
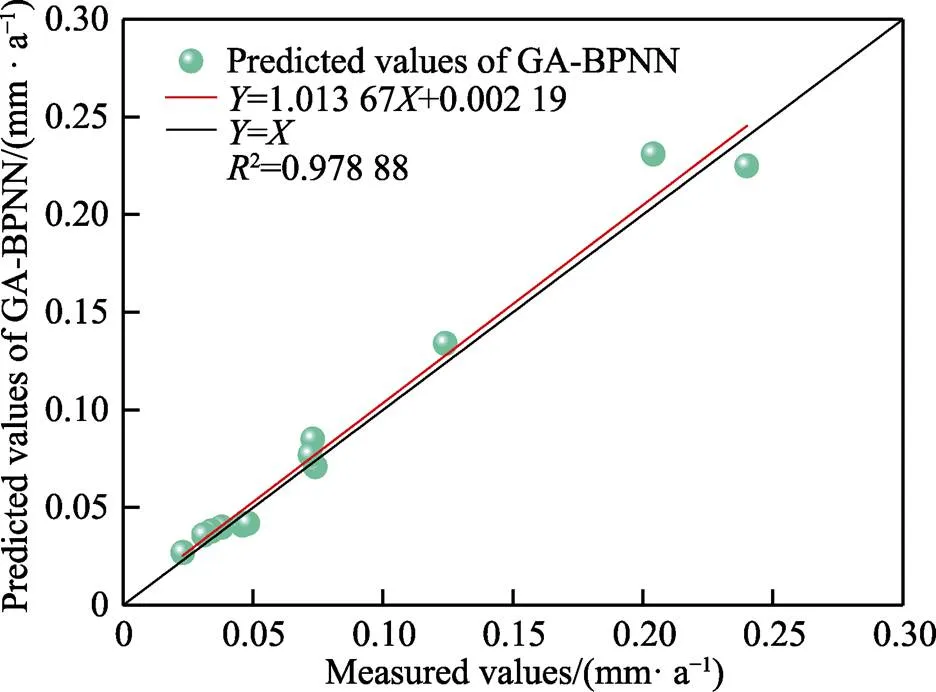
图7 GA-BPNN预测结果线性拟合图
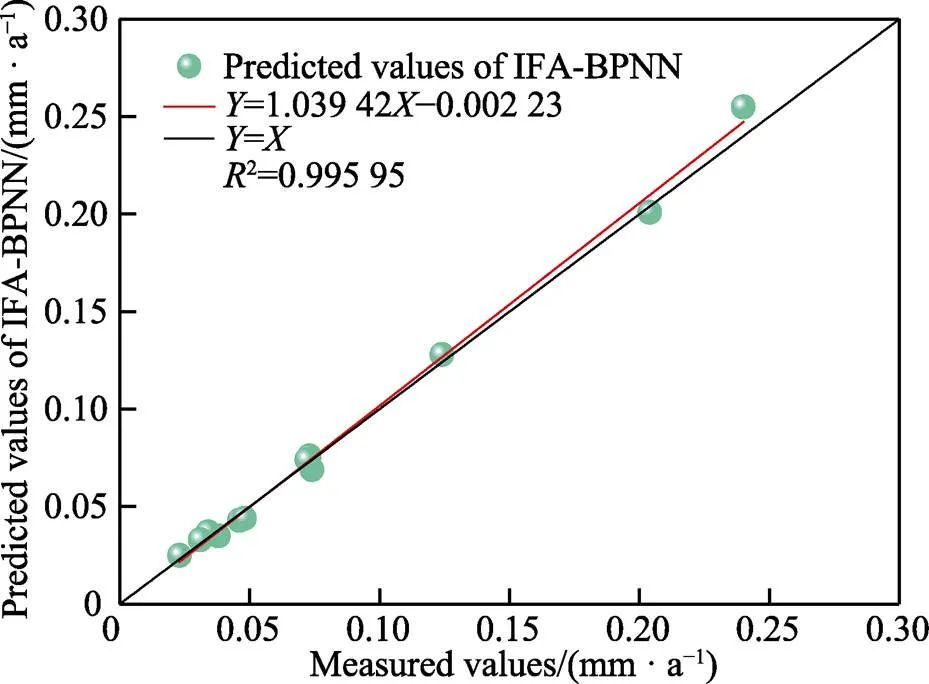
图8 IFA-BPNN预测结果线性拟合图
6 结论
1)对FA进行改进,一是对萤火虫初始位置进行Logistics混沌初始化,二是引入了新的惯性权重计算公式,有利于函数跳出局部最优寻找全局最优。利用改进的萤火虫算法优化BPNN的初始权值和阈值,建立了IFA-BPNN管道外腐蚀速率预测模型。
2)分别使用BPNN、PSO-BPNN、GA-BPNN以及IFA-BPNN模型对长输管道外腐蚀速率数据进行训练、预测。IFA-BPNN模型预测结果的MRE为5.94%,2为0.99595,均优于BPNN、PSO-BPNN、GA-BPNN的预测结果,验证了IFA-BPNN作为预测管道腐蚀速率工具的准确性和鲁棒性。应用IFA-BPNN模型预测管道外腐蚀速率可为长输管道的检维修提供决策支持。
3)由于管道外腐蚀因素较多,且工程上难以获取较为整齐的数据,后期研究可在数据集中添加随机变量以及噪音数据进行深入研究。
[1] 高鹏, 高振宇, 王峰, 等. 2018年中国油气管道建设新进展[J]. 国际石油经济, 2019, 27(3): 62-67. GAO Peng, GAO Zhen-yu, WANG Feng. New progress in China’s oil and gas pipeline construction in 2019[J]. International petroleum economics, 2019, 27(3): 62-67.
[2] 王大庆, 张鹏. 油气输送管线失效后果模糊事件树分析[J]. 安全与环境学报, 2014, 14(3): 88-92. WANG Da-qing, ZHANG Peng. Analysis of failure consequences of oil and gas transmission pipelines by using a fuzzy event tree[J]. Journal of safety and environment, 2014, 14(3): 88-92.
[3] 黄坤, 吴佳丽, 全恺, 等. 含腐蚀缺陷油气管道评价技术研究进展[J]. 表面技术, 2018, 47(1): 116-122. HUANG Kun, WU Jia-li, QUAN Kai, et al. A review on evaluation technology of oil-gas pipelines with corrosion defect[J]. Surface technology, 2018, 47(1): 116-122.
[4] 单克, 帅健, 杨光, 等. 美国油气管道基本失效概率评估方法及启示[J]. 油气储运, 2020, 39(5): 530-535. SHAN Ke, SHUAI Jian, YANG Guang, et al. Evaluation method for basic failure probability of oil and gas pipeline based on accident statistics in the United States and enlightenments[J]. Oil & gas storage and transportation, 2020, 39(5): 530-535.
[5] CHIO Lam, ZHOU Wen-xing. Statistical analyses of incidents on onshore gas transmission pipelines based on PHMSA database[J]. International journal of pressure vessels and piping, 2016, 145: 29-40.
[6] 张英, 吕佳慧, 王卫泽, 等. 失效数据库的建立和近年国内失效案例的统计分析[J]. 金属热处理, 2019, 44(1): 668-675. ZHANG Ying, LYU Jia-hui, WANG Wei-ze, et al. Establishment of failure database and statistical analysis of domestic failure cases based in recent years[J]. Heat treatment of metals, 2019, 44(1): 668-675.
[7] MOHAMMED S, ABBASY E, AHMED S, et al. Artificial neural network models for predicting condition of offshore oil and gas pipelines[J]. Automation in construction, 2014, 45: 50-65.
[8] 曲志豪, 唐德志, 胡丽华, 等. 基于优化随机森林的H2S腐蚀产物类型及腐蚀速率预测[J]. 表面技术, 2020, 49(3): 42-49. QU Zhi-hao, TANG De-zhi, HU Li-hua, et al. Prediction of H2S corrosion products and corrosion rate based on optimized random forest[J]. Surface technology, 2020, 49(3): 42-49.
[9] 凌晓, 徐鲁帅, 梁瑞, 等. 基于改进PSO-BPNN的输油管道内腐蚀速率研究[J]. 中国安全生产科学技术, 2019, 15(10): 63-68. LING Xiao, XU Lu-shuai, LIANG Rui, et al. Study on internal corrosion rate of oil pipeline based on improved PSO-BPNN[J]. Journal of safety science and technology, 2019, 15(10): 63-68.
[10] 马钢, 李俊飞, 白瑞, 等. 基于PSO-SVM模型的油气管道内腐蚀速率预测[J]. 表面技术, 2019, 48(5): 43-48. MA Gang, LI Jun-fei, BAI Rui, et al. Prediction of corrosion rate in oil and gas pipelines based on PSO-SVM model[J]. Surface technology, 2019, 48(5): 43-48.
[11] 王文辉, 骆正山, 张新生. 基于PSO-GRNN模型的埋地管道腐蚀剩余寿命预测[J]. 表面技术, 2019, 48(10): 267-275. WANG Wen-hui, LUO Zheng-shan, ZHANG Xin-sheng. Prediction on remaining service life of buried pipeline after corrosion based on PSO-GRNN model[J]. Surface technology, 2019, 48(10): 267-275.
[12] 张河苇, 金剑, 董绍华, 等. 一种基于管道大数据的腐蚀因素相关性分析方法[J]. 科学通报, 2018, 63(8): 777-783. ZHAN He-wei, JIN Jian, DONG Shao-hua, et al. A corrosion correlation analysis method based on pipeline big data[J]. Chinese science bulletin, 2018, 63(8): 777-783.
[13] 毕傲睿, 骆正山, 乔伟, 等. 基于主成分和粒子群优化支持向量机的管道内腐蚀预测[J]. 表面技术, 2018, 47(9): 133-140. BI Ao-rui, LUO Zheng-shan, QIAO Wei, et al. Prediction of pipeline inner-corrosion based on principal component analysis and particle swarm optimization-support vector machine[J]. Surface technology, 2018, 47(9): 133-140.
[14] 陈迪, 廖柯熹, 何国玺, 等. 基于EWM-GRA的腐蚀主控因素分析与腐蚀模型建立[J]. 表面技术, 2019, 48(6): 268-273. CHEN Di, LIAO Ke-xi, HE Guo-xi, et al. Analysis of corrosion main influencing factors based on EWM-GRA and corrosion model establishment[J]. Surface technology, 2019, 48(6): 268-273.
[15] 章玉婷, 杨剑锋. 基于BP神经网络的管道腐蚀速率预测[J]. 全面腐蚀控制, 2013, 27(9): 67-71. ZHANG Yu-ting, YANG Jian-feng. Corrosion rate prediction of pipeline based on BP artificial neural network[J]. Total corrosion control, 2013, 27(9): 67-71.
[16] 董绍华. 中国油气管道完整性管理20年回顾与发展建议[J]. 油气储运, 2020, 39(3): 241-261. DONG Shao-hua. Review of China’s oil and gas pipeline integrity management in the past 20 years and development suggestions[J]. Oil & gas storage and transportation, 2020, 39(3): 241-261.
[17] YANG X S. Firefly algorithms for multimodal optimization[J]. Lecture notes in computer science, 2009, 5792: 169-178.
[18] YANG, X S. Firefly algorithm, stochastic test functions and design optimisation[J]. International journal of bio inspired computation, 2010, 2(2): 78-84.
[19] YANG X S, HE X. Firefly algorithm: recent advances andapplications[J]. International journal of swarm intelligence, 2013, 1(1): 36-50.
[20] NANDY S, SARKAR P P, DAS A. Analysis of a nature inspired firefly algorithm based back-propagation neural network training[J]. Computer science, 2012, 8(22): 207- 220.
[21] HORNIK K, STINCHCOMBE M, WHITE H. Multilayer feedforward networks are universal approximators[J]. Neural networks, 1989, 2(5): 359-366.
[22] HOLLAND J H. Adaptation in natural and artificial systems[M]. Ann Arbor: University of Michigan Press, 1975.
[23] 许宏良, 殷苏民. 基于改进BP神经网络优化的管道腐蚀速率预测模型研究[J]. 表面技术, 2018, 47(2): 177- 181.XU Hong-liang, YIN Su-min. Prediction model of pipeline corrosion rate based on improved BP neural network[J]. Surface technology, 2018, 47(2): 177-181.
[24] 吉根林. 遗传算法研究综述[J]. 计算机应用与软件, 2004, 21(2): 69-73. JI Gen-lin. Survey on genetic algorithm[J]. Computer applications and software, 2004, 21(2): 69-73.
[25] SHI Y H, EBERHART R C. A modified particle swarm optimizer[C]//Proc of the IEEE international conference on evolutionary computation. Piscataway: IEEE Service Center, 1998: 69-73.
[26] CHATTERJEE A, SIARRY P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers and operations research, 2006, 33(3): 859-871.
[27] 程美英, 倪志伟, 朱旭辉. 萤火虫优化算法理论研究综述[J]. 计算机科学, 2015(4): 24-29. CHENG Mei-ying, NI Zhi-wei, ZHU Xu-hui. Overview on glowworm swarm optimization or firefly algorithm[J]. Computer science, 2015(4): 24-29.
[28] 杨雁莹, 徐仙伟, 曹霁. 基于仿生理论的新型优化算法综述[J]. 计算机仿真, 2016, 33(6): 233-237. YANG Yan-ying, XU Xian-wei, CAO Ji. Overview of new optimization algorithms based on bionic theory[J]. Computer simulation, 2016, 33(6): 233-237.
[29] 李巍华, 翁胜龙, 张绍辉. 一种萤火虫神经网络及在轴承故障诊断中的应用[J]. 机械工程学报, 2015(7): 99-106. LI Wei-hua WENG Sheng-long, ZHANG Shao-hui. A firefly neural network and its application in bearing fault diagnosis[J]. Journal of mechanical engineering, 2015(7): 99-106.
[30] ROBERT M. On the derivation of a “Chaotic” encryption algorithm[J]. Cryptologia, 1989, 13(1): 29-42.
[31] 李丹丹. 基于改进粒子群算法的混沌时间序列预测[D]. 秦皇岛: 燕山大学, 2014. LI Dan-dan. Chaotic time serise prediction based on improved particle swarm algorithm[D]. Qinhuangdao: Yanshan University, 2014.
[32] VELAZQUEZ J C, CALEYO F, VALOR A, et al. Technical note: Field study-pitting corrosion of underground pipelines related to local soil and pipe characteristics[J]. Corrosion, 2010, 66(1): 0160011-0160015.
[33] WANAS N, AUDA G, KAMEL M S, et al. On the optimal number of hidden nodes in a neural network[C]// Proceeding of 1998 IEEE canadian conference on electrical and computer engineering. Toronto: IEEE, 2002: 918-921.
Prediction of External Corrosion Rate of Oil Pipeline Based on Improved IFA-BPNN
1a,1a,2,1a,1a,1b
(1.a.College of Petroleum and Chemical Engineering, b.College of Sciences, Lanzhou University of Technology, Lanzhou 730050, China; 2.PetroChina Gansu Lanzhou Marketing Company, Lanzhou 730050, China)
In order to establish a machine learning model for predicting the external corrosion rate of long land transport pipelines, improve the prediction accuracy of the external corrosion rate of the pipeline, and accurately grasp the external corrosion status of the long-distance pipeline, this paper analyzes the working principle of FA, to solve the problems of FA, such as local optimization or function convergence failure due to initial parameter setting, and an improved FA algorithm is proposed: This paper uses the method of Logistics chaotic mapping to initialize the position of the firefly, and improve the cultivability of the firefly population; this paper introduces a new inertia weight calculation method to improve the formula of the firefly position movement and enhance the FA global optimization ability. The improved FA (IFA) was used to optimize the initial weights and thresholds of BPNN, and a long-distance pipeline external corrosion rate prediction model based on IFA-BPNN was established. Taking 111 sets of long-distance pipeline external corrosion detection data as an example, the simulation calculation is carried out in MATLAB, and PSO-BPNN, GA-BPNN and unoptimized BPNN are used as comparative models for comparative analysis. The IFA model is used to initialize the BPNN model, which greatly improves the prediction accuracy of the BPNN model. The IFA-BPNN model was used to predict and analyze the external corrosion rates of 12 groups of pipelines, the average relative error was only 5.94%, and the2of the prediction results was 0.995 95. The prediction results of IFA-BPNN model are superior to those of BPNN model, PSO-BPNN model and GA-BPNN model in all aspects. IFA-BPNN has good accuracy and robustness as a tool to predict pipeline corrosion rate.
firefly algorithm; BP neural network; chaos initialization; inertia weight; oil pipelines; corrosion rate prediction
2020-07-30;
2020-11-27
LING Xiao (1982—), Male, Doctor, Associate professor, Research focus: oil and gas pipeline integrity management. E-mail: lingxiao_ lut@163.com
凌晓, 徐鲁帅, 高甲程, 等.基于IFA-BPNN的长输管道外腐蚀速率预测[J]. 表面技术, 2021, 50(4): 285-293.
TG172
A
1001-3660(2021)04-0285-09
10.16490/j.cnki.issn.1001-3660.2021.04.029
2020-07-30;
2020-11-27
国家自然科学基金青年项目(51904138);甘肃省自然科学基金(20JR5RA451);甘肃省高等学校创新能力提升项目(2020A-019)
Fund:Supported by the Youth Program of National Natural Science Foundation of China (51904138); the Natural Science Foundation of Gansu Province (20JR5RA451); Innovation Ability Improvement Project of Colleges and Universities in Gansu Province (2020A-019)
凌晓(1982—),男,博士,副教授,主要研究方向为油气管道完整性管理。邮箱:lingxiao_lut@163.com
LING Xiao, XU Lu-shuai, GAO Jia-cheng, et al. Prediction of external corrosion rate of oil pipeline based on improved IFA-BPNN[J]. Surface technology, 2021, 50(4): 285-293.
