无穷积分余项与其被积函数比值的收敛阶

王凤琼

(成都信息工程大学 应用数学学院，成都610225)

1 引 言

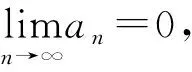
以例子形式给出两个简单情形的对应比值结束本节.

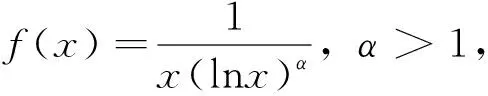
2 主要结果

对q>0，Gamma函数的余项

有如下结论[5]

Γ(q，x)～xq-1e-x(x→+∞).

(1)

命题1对于c>0，α>0和β>-1， 设

证令u=ctα，则由式(1)，得

因此当x→ +∞时，有

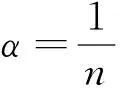
但一般情形， 有

(2)

注2 由洛必达法则， 有

记Fα(x)=Fα，0(x)， 下面考虑它在区间[0，+∞)上的单调性， 依据文[3]定理1和2 的思路可以得到如下结果:

命题2当0<α<1 时Fα(x)在[0，+∞)上严格单增， 当α>1时Fα(x)在[0，+∞)上严格单减.

证记φα(x)=φα，0(x). 计算得到

F′α(x)=αcxα-1Fα(x)-1=αcxα-1e-cxαfα(x)，

(3)

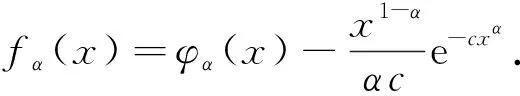
进而， 有

因此对x∈(0，+∞)， 当0<α<1时有fα(x)>0， 当α>1时有fα(x)<0. 故由式(3)得到Fα(x)在区间[0，+∞)上的单调性.

将命题1的结论应用到Mittag-Leffler函数[6]， 这个函数与分数阶微积分以及分数阶微分方程有着紧密关系.

对于Mittag-Leffler函数

文[6]得到

于是当x→ +∞时， 有

(4)

(5)

下面令

(6)

为继续下去， 需要如下引理([4]， 第三章第10节，P63-64).

于是由式(4)-(6)和引理1， 当x→ +∞时有

其中最后一个等价由式(1)得到. 可见， 仍然与β无关.

3 级数情形

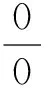
引理2[7](Stolz定理) 设两个实数列{xn}，{yn}满足:

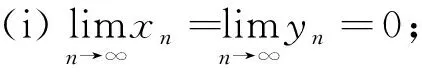
(ii) {yn}严格递减；

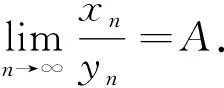
证当x→0时有(1+x)θ-1～θx， 其中θ为一个常数. 由引理2， 有

(7)

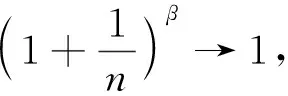
从而

所以

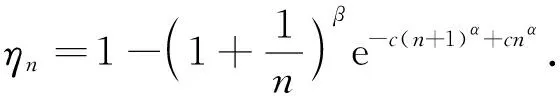
所以

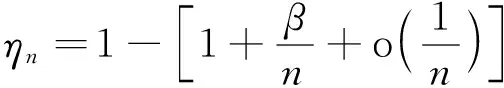
故

4 结 论

致谢本文得到高等学校大学数学教学研究与发展中心2019年项目和成都信息工程大学教改项目的支持， 文献[3，4，6]给予本文很大的启示， 审稿人的意见改进了本文， 在此一并表示感谢!