Mathematica在镜像法求解静电场边值问题中的应用

曹 蓉，汪梦雅，夏杰桢，吴 琪

(西藏大学 理学院，西藏 拉萨 850000)

《电动力学》课程因其较深的数学理论和场的抽象性使得学生在学习中往往有恐惧心理，很难产生学习兴趣。静电场的边值问题是“电动力学”课程的重要内容之一，当求解的区域内只有一个或几个点电荷,区域边界是导体或介质界面,对于这样的区域电场的求解可以采用一种特殊的方法——镜像法。虽然镜像法求解静电场边值问题的步骤和思路较为简单，但是利用镜像法所求得的物理问题的数学表达式往往比较繁杂，学生也很难通过最后求解的数学表达式去理解复杂的场的空间分布，进而阻碍了学生对问题的物理认识。

因此为了更好地理解场的空间分布特点，绘制随空间变化的可视化图形是非常必要的。因此本文系统且全面的按照空间区域具有球面、柱面或无限大平面等几何对称性边界的几种情况，讨论了空间中点电荷或线电荷不同分布情况下的几种典型的镜像法求解静电场边值问题，得出该区域的电势分布和场强分布。并借助Mathematica 系统内设的“绘制矢量场”的功能绘制出其等势线和电场线图，实现了场图的可视化，进而帮助学生从复杂的数学结果中提炼直观的物理认识，有助于学生深入认识静电场中镜像法的本质和规律。

1 镜像法理论

镜像法[1]是求解静电场边值问题的一种特殊方法，这种求解方法的主要思想是将静电场边值问题中边界对场的影响用求解区域外部假设的镜像电荷来取代，镜像电荷放在边界的外部，它的存在不会改变所要研究区域内电荷的分布，只要调整镜像电荷的位置和大小，使得它产生的场和原电荷分布所产生的电场满足给定的边界条件要求，同时以静电场唯一性原理为理论依据，可以找到满足条件的解。

2 平面导体界面的镜像

2.1 点电荷对无限大接地导体平面的镜像

点电荷与接地导体边界问题是镜像法应用的一个典型例子，如图1(a)(b)所示。

在求解区域中电位满足：

∇2φ=0，φ|导体板位置=φ|r→∞=0

(1)

采用镜像法，用镜像电荷来代替导体板上的感应电荷后，新系统满足：

(2)

根据静电场唯一性原理：方程相同，边界条件相同，那么解就是唯一的。因此这两个系统的解就是一样的，以r表示原电荷到场点P的距离，r′表示镜像电荷q′到P点的距离，设原电荷到导体板的距离为a，则P点的电势为：

(3)

图1(a) 点电荷与无限接地导体

电势分布图清楚的显示：导体板上方的电势大于零，导体板上下电势在导体板面处连续。

电场强度大小分布图清楚的显示：在靠近点电荷附近处电场变强，而在远离点电荷最远的导体板上下两侧，电场最弱。在导体板上方，表示电场强度方向的箭头都是垂直指向导体板下方的，这说明导体板是等势面，而且感应电荷是负的。

2.2 无限长线电荷对无限大接地导体平面的镜像

如图2(a)(b)所示的系统跟点电荷模型是类似的，找同样的镜像线电荷，只不过此时等效的是线电荷密度，该模型原来满足的方程和边界条件为：

(4)

依据静电场唯一性原理，等效替换后可以求出上半空间的电位分布为：

(5)

同样利用Mathematica软件[3]求出电势及电势的梯度，得出场强x和z方向的分量表达式，然后根据这些表达式绘制出电场强度大小和电场强度方向的分布图，最后用Show命令将场强方向和等势线合并起来，结果如图2(c)(d)所示。

图2(a) 线电荷与无限接地导体

电势分布图清楚的显示：导体板上方的电势大于零，导体板上下电势在导体板面处连续。

电场强度大小分布图的特点和点电荷与无限大接地导体板镜像的分布基本是一样的。

2.3 点电荷对相交半无限大接地导体平面的镜像[4]

对于如图3(a)(b)所示的系统，当加入镜像电荷时，需要满足原来的边界条件，即该无限大接地导体的电位为零，那么要想让导体板(下)的电位为零，需要在其对称的位置放一个等量负镜像电荷，同时还得让导体板(左)的电位为零，同样根据对称性，放一个等量负镜像电荷，显然此时导体板的电位不满足为零，这时需要在导体板斜对角的对称位置放一个等量正镜像电荷，此时，这四个电荷在边界产生的电位为零，根据分析可知，需要引入三个镜像电荷才能满足要求。则求解区域范围内场点的电势为：

q=-q1=-q2=q3

(6)

(7)

运用mathematica软件画图时，取点电荷的坐标为(1,1)，三个镜像电荷的坐标也按单位长度取。此时可以画出该系统的电势空间分布图和电场强度分布图，如图3(c)(d)。

(a)

从图上可以看出在靠近点电荷附近处电场变强，在导体板左方，表示电场强度方向的箭头都是垂直指向导体板左方的，这说明导体板是等势面，而且镜像电荷是负的，同样导体板下方也是一个负的镜像电荷，位于导体板左下角处也有一个镜像电荷，它的电场方向是指向右上方的，说明它是一个正的镜像电荷。

3 导体球面的镜像

3.1 点电荷位于接地导体球面外

解决这个问题同样用镜像法，以球心为坐标原点，点电荷在X轴的延长线上，如图4(a)所示，可以知道球面处的电位处处相等且为零，因此满足边界条件：

∇2φ=0，φ|r→∞=φ|球面=0

(8)

由于无法确定感应负电荷的分布，因此直接计算也是不容易的。本文假设镜像电荷的位置如图4所示，且满足的边界条件，即令球面电位等于零

(9)

同时r1,r2分别满足

(10)

将r1,r2分别代入到(9)中可得

[q2(b2+R2)-q′2(d2+R2)]+2R(q′2d-q2b)cosθ=0

(11)

由于要对所有的角度都成立，所以cosθ前的系数必须等于零，且另一项也必须等于零，即

q′2d-q2b=0，q2(b2+R2)-q′2(d2+R2)=0

(12)

得到镜像电荷的位置以及镜像电荷的大小

(13)

因此，球面由镜像电荷-q′等效替换后，球面可视为不存在，此时球外任一点p的电位和电场为

(14)

根据电势和场强的表达式，编写相关的程序[5]，得到电势的空间分布图和等势线与电场强度方向的合并图。如图4(b)(c)所示。

(a)

3.2 点电荷位于不接地导体球面外

(15)

(16)

该系统的Mathematica的画法跟接地系统[6]的画法是相似的，同样编写出相关程序，就可以画出系统的电势分布图和场强方向与等势线的结合图，如图4(e)(f)。

图4(b)清楚的显示，球内的电势恒为零，球外的电势大于零，并且球内外电势在球面是连续的。图4(c)表明，球内的电场恒为零，球外的电场发生突变，从图上可以看出，越靠近点电荷附近，电场强度越强，同时远离点电荷处，电场越弱。同时可以看出在球面的外侧，电场强度的方向全部垂直指向球面里，这说明导体球面是等势面，且设想的镜像电荷是负的。

图4(e)清楚的显示，导体球面是电位不为零的等位面，球外的电势大于零，并且球内外电势在球面是连续的。图4(f)表明，球内的电场恒为零，球外的电场发生突变，从图上可以看出，越靠近点电荷附近，电场强度越强，同时远离点电荷处，电场越弱。同时可以看出在球面的外侧，电场强度的方向全部垂直指向球面里，这说明导体球面是等势面，且镜像电荷是负的。

4 导体圆柱面的镜像

4.1 线电荷与接地导体圆柱面的镜像[7]

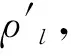
(17)

由于导体圆柱接地，即导体边界电位为零，因此有

(18)

上式对θ求导，可以得到

(19)

化简得

(20)

利用Mathematica软件可以实现该结果的可视化[8]，编写电势和场强的相关程序，画出的图形如图5(b)(c)所示。

(a)

4.2 两平行导体圆柱面的镜像

根据上述线电荷与接地导体圆柱面的镜像方法，只需要将线电荷看成两个半径相同，带有等量异号电荷的平行导体圆柱面。由于正负电荷互相吸引，因此在这两个导体靠近的地方电荷分布密集，而两侧电荷分布稀疏，但具体电荷是怎样分布是不确定的。此时满足的方程和边界条件分别是：

∇2φ=0

(21)

(22)

利用镜像法，用一根无穷长的细导线来等效替代。可以计算出任一点P的电位。

那么电位就可以通过场强积分得到，即

(23)

利用Mathematica绘制出两平行导体圆柱面的电势和电场分布图，如图5(e)(f)所示。

图5(b)清楚的显示，导体圆柱面上的电势恒为零，线电荷的电势大于零，镜像线电荷的电势小于零。图5(c)表明，越靠近线电荷附近，电场强度越强，同时远离线电荷处，电场越弱。同时可以看出在导体圆柱面的外侧，电场强度的方向全部垂直指向里面，这说明导体圆柱面是等势面，且镜像电荷是负的。

电势分布图5(e)清楚的显示：正的导体圆柱面的电势大于零，负的导体圆柱面的电势小于零，且在等势面上它们是连续的。

电场强度大小分布图5(f)清楚的显示：在靠近点电荷附近处电场变强，而在远离点电荷处电场最弱。正的点电荷处，表示电场强度方向的箭头都是垂直向外的，负的点电荷处，电场强度的方向是向里的。

5 电荷无限大介质分界平面的镜像

这个系统有两层介质且都是半无穷大的，中间有一个分界面，显然这个系统的电场分布与之前导体的分析有所不同，因为导体是等电位的，但介质不同，如图6(a)所示的点电荷必然会向周围产生电力线，且电力线会穿过下方的介质，这样的话就会使得下方介质出现极化，极化会形成电偶极子，而电偶极子产生的场又难以分析，所以根据前面的分析，可以知道，下方介质产生的场相当于极化体电荷和极化面电荷共同产生的，如果是均匀介质，则极化体电荷的密度为零，因此只有极化面电荷，但不知道这些电荷是正电荷还是负电荷，所以直接分析还是比较难的，此时可以想到还是利用镜像法[9]解决，那么关键就是如何确定镜像电荷的位置，如果在下方介质中的对称位置放一个镜像电荷，依然无法确定电荷的电量，也无法确定电荷的个数，同时放入镜像电荷的话，下方介质中的电场分布也难以分析。因此对于这样的系统可以采用二次镜像法来分析，如图6(b)(c)所示：

将下方介质换成上方介质，再在对称位置放一个镜像电荷q′，如果要求下方介质电场的分布，那么注意此时的镜像电荷q″应该放在上方。从物理角度分析，分界面上方的电场由q与q′共同产生，q′等效替代极化电荷的影响，分界面下方的电场由q″决定，且用来代替自由电荷和无穷多个极化电荷的作用。那么这种代换是否正确，就需要通过唯一性定理证明，这个系统的方程和边界条件分别是：

∇φ1=0,∇φ2=0

(24)

(25)

(26)

还是用Mathematica软件，画图时将场分成两个不同介质的区域，分别编写相应的程序进行计算即可。得到的场图如图6(d)(e)所示。

(a)

图6(d)(e)表明，导体圆柱面上的电势恒为零，线电荷的电势大于零，镜像线电荷的电势小于零。图6表明，越靠近线电荷附近，电场强度越强，同时远离线电荷处，电场越弱。同时可以看出在分界面的上方，电场强度的方向全部垂直指向分界面下方，这说明分界面下方设想的镜像电荷是负的。

6 结 语

镜像法是求解静电场边值问题的一种特殊方法，然而教材上对镜像法的讲解比较简单。因此本文在课本内容的基础上，系统且全面的按照空间区域不同的几何对称性边界(球面、柱面或无限大平面)，讨论了空间中点电荷或线电荷不同分布情况下的几种典型的镜像法求解静电场边值问题。利用Mathematica对复杂的数学结果进行了数值模拟[10],并绘制了相应的直观的等势线和电场线图,这将有助于学生深入理解“电动力学”教材中静电场镜像法的内容，同时对于静磁场镜像法场图的可视化也有一定的启发和借鉴意义。