基于MATLAB的地磁场中带电粒子运动模拟分析

钟海坚，陈宗华，赵炳炎

(玉林师范学院 物理与电信工程学院，广西 玉林 537000)

宇宙中的高能粒子对航天器的具有强大的破坏作用，如果宇宙高速粒子直接射向地球空间环境将对航天航空[1,2]，广播通信以及电力等领域产生重大影响。自1958年探索者1号上的盖格计数器发现范艾伦辐射带以来研究人员就对它进行持续不断的研究，目前关于范艾伦辐射带中粒子的来源、分布、传输以及损耗等方面的已经取得了一定的成果。

研究带电粒子在地磁场中的运动有助于了解范艾伦辐射带对地球电磁环境的保护作用，预测太阳异常活动或太空天气变化引发地磁场粒子异常活动对相关领域可能产生的影响[3]。本文主要基于磁偶极场模型，从带电粒子在电磁场中的运动方程出发，利用数值计算的方法对带电粒子在地球磁场中的部分运动情况进行分析并讨论粒子的弹跳运动、漂移运动和抛射角范围。

2 物理模型及基本方程

2.1 无太阳风影响模型

在某种情况下地球可认为是一个巨大的磁偶极子。所以，这里地磁场用偶极场近似，其模型[4]为

(1)

(2)

2.2 有太阳风影响模型

因为自然界的磁现象均可以等效为若干个偶极场的叠加[5,6]，所以用两个偶极场叠加对受太阳风影响的地磁场做近似，取

(3)

根据式以地心为坐标原点建立空间直角坐标系求出x,y,z∈[-75Re,75Re]区域的磁感应强度大小，利用MATLAB的streamline函数画出磁感线，得到如图1所示地球磁场磁感线分布图。

由图1可知，在近地空间中向阳侧磁顶层受太阳风影响其形状近似半球，同时背阳面的磁力线向后延伸形成磁尾这与真实地磁分布类似。

图1 地球磁场磁感线分布

3 地球磁场中带电粒子的运动方程

在近地空间中，带电量为q，质量为m，速度为v，能量为10 MeV的粒子，在电场强度为E磁感应强度为B的场中运动，其所受的电磁场作用力由洛伦兹力公式[7]给出

(4)

其中，γ为相对论因子γ=(1-v2/c2)-(1/2)，考虑到E(r)=0，故式可以写成如下分量形式

随着湖南省“一带一部”新战略的推进，湖南希望逐步发展成为中国中西部地区新兴增长极，成为沟通东西、连接南北的中国重要交通枢纽，成为生态文明体制机制创新示范区，这些目标的实现无疑都离不开城市化与生态环境的协调持续发展。

(5)

式为二阶微分方程组，由于难以找到解析解，故需进行数值求解。

4 带电粒子在地磁场中的运动轨迹

以太阳风中的一束粒子为研究对象，研究在地球磁场中质子的运动轨迹。粒子的带电量为e=1.602 176 565×10-19C，质子的质量为m=1.672 621 777×10-27kg，粒子的起始位置为(4Re,0,0)，入射速度与磁场的夹角(抛射角)为30°，粒子的动能为10 MeV。根据式计算得出该粒子在地磁场中的运动轨迹，如图2所示。

图2 质子在地磁场中运动轨迹

4.1 粒子在地磁场中的弹跳运动

在能量大于105eV的中高能粒子研究中，可以不考虑电场(旋转电场和Volland对流电场)的影响[8]，所以作用在粒子上的力只有洛伦兹力，粒子的动能Ek=Ek⊥+Ek‖=恒量。由于地磁场纵向是非均匀的，所以穿过粒子回旋半径圆的磁感线不垂直于该圆所在的平面，洛伦兹力可分解为垂直于磁场的分量F⊥和平行于磁场的分量F‖。其中，洛伦兹力平行于磁场的分量F‖指向弱磁场的区域，它使从弱磁区向强磁区运动粒子速度的纵向分量v‖不断减小直至为零，然后将其反向加速，粒子完成一次弹跳运动，如图3所示。

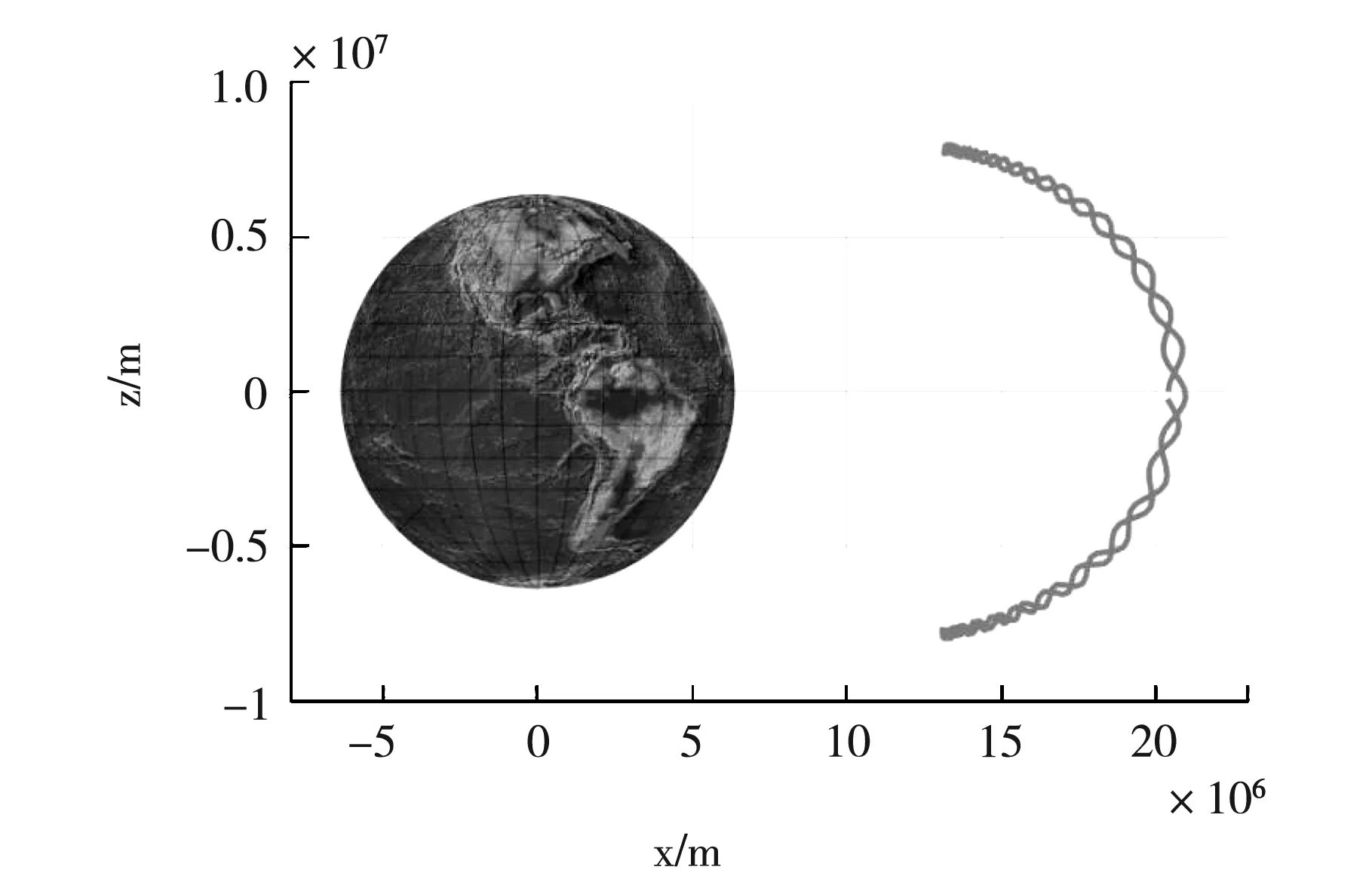
图3 带电粒子在地磁场中的弹跳运动

由此可知，地磁场的磁镜结构使得以一定角度射入地磁场的带电粒子一直做往返于两磁极的弹跳运动被束缚在地磁场中。地磁场的磁镜结构可以将太阳风中的中高能带电粒子束缚在其中对地球空间环境起到了保护作用。

4.2 带电粒子在地磁场中的漂移运动

在研究粒子的漂移运动时，粒子的运动可视为绕引导中心的运动和引导中心沿磁力线运动的叠加[9]。此时，引导中心具有平行于磁感应强度B方向的速度分量v‖，粒子受到惯性离心力作用发生漂移运动，即曲率漂移。粒子所受的惯性离心力为：

(6)

其中，rc的大小为磁力线的曲率半径,方向指向磁力线弯曲外侧的法向。对应的曲率漂移速度[10]为：

(7)

由地磁场的磁场强度分布形状知，地磁场在横向上为非均匀分布，磁场的横向梯度将对粒子产生力的作用，该作用力为：

F=∇(pm·B)=-pm∇B

(8)

其中，pm为粒子绕引导中心运动的磁矩。

在此作用力下，带电粒子将做垂直于磁场方向的漂移运动，即梯度漂移。其速度为：

(9)

由此可知，粒子在地磁场中的曲率漂移和梯度漂移的速度取决于粒子的性质：正、负粒子的漂移方向相反，能量越大的粒子漂移速度越大。

4.3 带电粒子在地磁场中的抛射角

由于地磁场是一个天然的磁镜，在研究带电粒子的抛射角大小与对应的磁镜点位置关系时，使用磁镜的理论来研究。

(10)

从图4得知，从(4Re,0,0)点抛射出粒子的磁镜点的磁感应强度大小由粒子的抛射角决定，当粒子的抛射角小于1.11°，粒子的磁镜点到地面的距离将小于100 km，此时粒子将会与地球大气碰撞在反射前损失在地球大气层中[8,12]；当粒子的抛射角在1.11°～89.61°时，随着抛射角增大磁镜点的磁感应强度先快速减小然后趋于不变。这主要是受到粒子曲率漂移影响的结果。

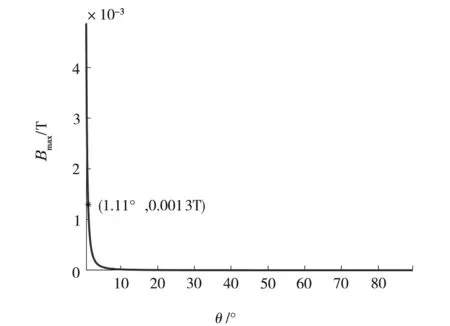
图4 抛射角与磁镜点磁感应强度的关系

5 结 论

本文针对带电粒子在地磁场中的运动方程利用MATLAB的ode45算法对运动方程进行数值求解，同时，对带电粒子在磁场中的运动过程进行仿真，进一步分析了带电粒子的运动构成，粒子的抛射角对粒子在地磁场中运动的影响，得到如下结论：

(1)地磁场的磁镜结构使得带电粒子在两磁极间做弹跳运动，为地球磁层阻挡宇宙高速粒子保护地球电磁环境奠定基础

(2)对于带电粒子在地磁场的漂移运动，带电粒子在地磁场中的漂移运动由粒子的性质决定，正、负粒子的运动方向相反，运动速度大小与粒子的能量相关，能量越大的粒子运动速度越大。

(3)带电粒子的抛射角越大，磁镜点的磁感应强度越小，随着抛射角增大磁镜点的磁感应强度先快速减小然后趋于不变，当抛射角小于1.11°时，带电粒子在反射前将损失在大气层中。