基于背应力功的疲劳能量模型及其在轮槽构件寿命预测中的应用

王 琦，王恭义，程 凯，徐海丰，舒润民，叶笃毅

(1.浙江大学能源工程学院，浙江杭州 310027;2.上海汽轮机厂有限公司，上海 200240)

1 前 言

汽轮机转子轮槽在服役过程中通常承受叶片离心载荷作用[1]。在汽轮机启停与变负荷工况下，轮槽齿根处于拉平均应力下的交变载荷作用(如图1所示)，并由此引起轮槽结构出现疲劳失效。因此，对汽轮机转子轮槽进行疲劳寿命预测是汽轮机疲劳强度设计的重要内容之一。

图1 转子轮槽示意图(a)及其承受的交变载荷(b)Fig.1 Schematic diagram of rotor groove(a)and its carried alternating loads(b)

目前对汽轮机转子轮槽构件进行疲劳寿命预测主要是基于局部应力-应变法[2]。近年来，随着对疲劳损伤机制研究的深入，在局部应变法基础上发展起来的能量方法，以其物理意义明确、预测精度高等优点，受到了工程结构疲劳强度设计者的普遍欢迎[3-4]。疲劳寿命预测能量方法认为，材料产生不可逆疲劳损伤的根本原因是循环塑性功的累积，当累积塑性功达到临界值时，材料发生疲劳破坏[5]。Halford[6]根据塑性应变产生不可逆疲劳损伤，推导了以循环塑性应变能为基础的疲劳损伤预测模型。Golos和Ellyin[7]在塑性应变能模型基础上，进一步考虑平均应力的影响，提出了疲劳损伤总应变能理论。最近，Ayhan Ince等[8]基于循环塑性应变能，考虑正/负平均应力的影响，发展了一种基于畸变能的疲劳寿命预测模型。尽管能量法在疲劳寿命预测研究中呈现良好的发展前景，但现有的疲劳损伤能量模型大多忽略了疲劳损伤过程中的能量耗散现象[9]。根据热力学原理，外界对物体做功产生的塑性应变能的一部分以位错、缺陷等形式储存于材料内部(即储能)，并由此产生疲劳损伤，而绝大部分塑性应变能则以热量等形式耗散掉。因此，根据疲劳损伤的能耗结构，目前以循环应变能为基础的疲劳损伤能量模型将不可避免地高估了循环塑性应变能在实际疲劳损伤中的贡献。

最近，徐海丰等[10]在疲劳损伤能耗分析基础上，通过将循环塑性应变能分解为背应力塑性功和摩擦应力塑性功，并赋予了两者明确的物理内涵，即：背应力塑性功与疲劳损伤过程中的储能有关，而摩擦应力塑性功与热耗散现象相联系，据此发展了一种基于背应力塑性功累积的疲劳损伤能量模型。上述模型在光滑试样的疲劳寿命预测中取得了良好结果。本研究主要结合某汽轮机转子轮槽结构件的疲劳寿命预测，从循环过程中轮槽齿根部位背应力塑性功累积角度，来研究轮槽构件的疲劳寿命预测能量模型，并通过轮槽模拟件的疲劳试验来初步验证该新的能量模型的有效性和预测精度。

2 基于背应力塑性功累积的缺口件疲劳寿命预测能量模型

研究采用的缺口件疲劳寿命预测以局部应力-应变法为基础，其计算流程可归结为：首先由作用载荷确定结构件缺口根部局部应力应变，然后，计算危险部位的疲劳损伤，最后，采用损伤累积法则预测构件疲劳寿命。

2.1 缺口根部局部应力应变计算

叶笃毅等[11，12]基于热力学原理，提出了一种以储能为基础的缺口局部应力应变近似计算方法，其表达式可写成：

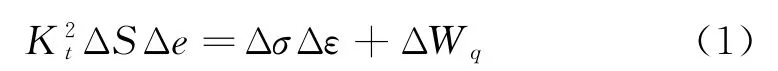
式中，ΔWq(=ΔWp-ΔWs)，是一个循环过程中耗散的热量，ΔWp为循环塑性应变能，ΔWs为储能(如图2所示)。当材料满足幂硬化规律(RO 模型)时，ΔWq也可近似表示为：

因此，结合RO 模型[13]，式(1)可进一步写成：

图2 循环加载下弹塑性体的塑性应变能ΔW p 和储能ΔW sFig.2 Plastic strain energy and storage energy of an elastic-plastic body subjected to cyclic loading

2.2 缺口根部材料疲劳损伤计算

首先以图3(a)所示的具有拉平均应力的某一循环为例来给出材料内应力之间的关系，图中，σmax为峰值应力；σa和σm分别表示一个循环中的应力幅和平均应力；σB和σF为背应力和摩擦应力，其中，背应力对应了材料中位错长程作用力，而摩擦应力与材料中位错短程作用力有关[14]。

图3 具有拉平均应力的迟滞回线(a)及内应力功组成(b)(ΔWpB和ΔWp F分别表示某个循环中背应力与摩擦应力所作的功)Fig.3 Hysteresis loop with a mean stress(a)and its constituteof the internal stress work(b)

根据图3(a)，摩擦应力可由下式确定：

对于大多数材料，背应力与塑性应变幅满足幂函数关系[10]：

式中，Kb和nb为与材料相关的常数。

联立式(4)和式(5)可得到摩擦应力的表达式：

式中，Δσ 为应力范围，Δεp为塑性应变范围。

联立式(6)和式(7)可进一步得到：

参照塑性应变能理论[6]中稳定循环塑性应变能-疲劳寿命之间的关系来构造背应力塑性功与疲劳寿命的表达式，则可得到：

式中，Nf为疲劳寿命，X 和α 为与材料相关的常数。

根据摩擦应力和背应力的物理意义[10]，即：摩擦应力做功主要与材料热耗散现象相联系，而背应力做功主要对应了材料内部的储能增加。因此，可基于疲劳过程中背应力塑性功累积来预测疲劳损伤能耗。

当结构件的缺口根部存在平均应力时，由于缺口根部材料屈服通常会引起平均应力松弛，因此，实际缺口部位平均应力影响将随循环变形逐渐减小[15]。Attilio[16]以流变模型为基础提出一种预测平均应力松弛的模型如下：

因此，当考虑平均应力循环松弛时，对应某个循环(N)下的背应力塑性功表达式可进一步写成：

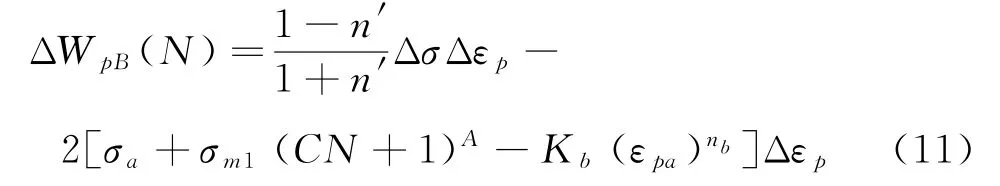
上式表明，即使外载荷保持恒定，缺口根部由于平均应力循环松弛，疲劳过程中的背应力塑性功也将呈现循环变化的特征。将上述疲劳过程中循环变化的背应力塑性功累积视为损伤累积过程，则对应某个循环下的疲劳损伤可由式(11)结合式(9)得到：

上式表明，第N 个循环下的疲劳损伤(DN)为当前循环(N)下背应力塑性功(ΔWpB(N))的函数，因此，采用Miner线性累积损伤法则可计算结构件的疲劳寿命为：

式中，n 为考虑缺口根部平均应力松弛的结构件疲劳寿命。

3 某型汽轮机轮槽构件的疲劳寿命预测及试验验证

3.1 轮槽材料低周疲劳特性参数

用于汽轮机轮槽构件疲劳寿命预测的材料低周疲劳特性参数如表1所示。由于该材料在疲劳过程中主要呈现疲劳软化现象，并由此影响平均应力的循环松弛行为，因此，首先采用式(10)结合轮槽材料在脉动循环载荷(R=0)下的平均应力松弛试验结果，确定轮槽材料的平均应力松弛模型为：

式中，εa是作用应变幅。

表1 轮槽材料低周疲劳特性参数Table 1 Low cycle fatigue characteristic parameters of the rotor groove material

3.2 轮槽构件低周疲劳寿命预测

用于疲劳寿命预测的某汽轮机轮槽模拟构件几何形状如图4(a)所示，各齿根的应力集中系数通过有限元计算获得(如表2)，其中A 齿根的理论应力集中系数最大，应力集中现象最为严重，因此，本次疲劳寿命预测主要针对A 齿根进行。

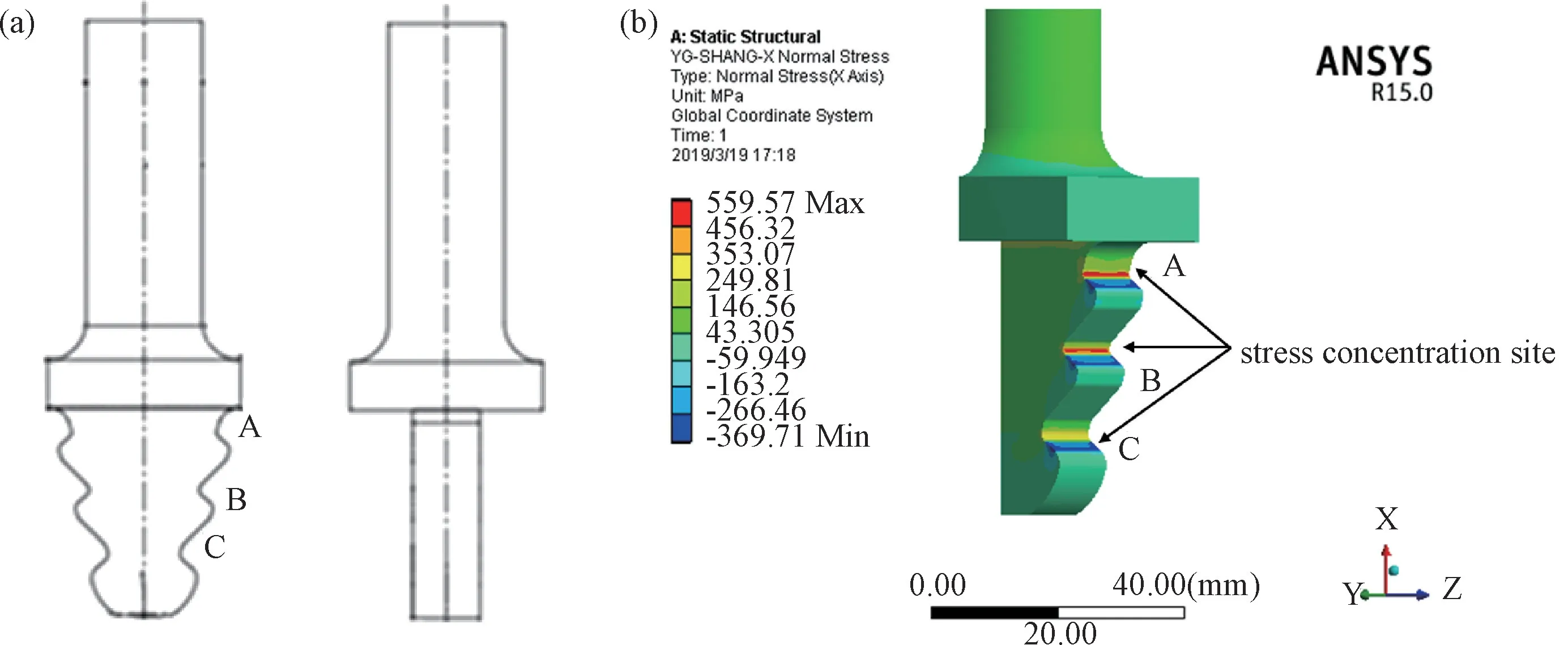
图4 轮槽模拟件几何形状(a)及有限元应力分析结果(b)Fig.4 (a)Wheel groove simulates part geometry(b)Results of finite element stress analysis

表2 轮槽构件各缺口的理论应力集中系数Table 2 Theoretical stress concentration coefficient of each notch of a rotor groove sample

轮槽构件疲劳寿命预测通过Matlab编程实现，寿命预测流程如图5所示。

为了证明建立的基于背应力塑性功累积的疲劳寿命预测模型较传统的基于应变能的能量模型更具优势，这里同时采用传统总应变能预测模型对图4(a)中轮槽构件进行疲劳寿命预测，总应变能疲劳寿命预测模型详见参考文献[7]。

3.3 轮槽构件的低周疲劳试验

为了验证建立的疲劳损伤能量模型的预测精度，进行了图4(a)中轮槽构件的低周疲劳试验。根据汽轮机运行过程中转子轮槽实际承载情况(脉动载荷，如图1b)，疲劳试验采用应力比R=0的轴向载荷控制，正弦波加载，试验采用4 级名义载荷(200 k N，210 k N，220 k N，240 k N)进行。试验过程中采用高倍率读数显微系统定期观察轮槽齿根部位的裂纹发展情况，并以轮槽齿根A处观察到0.5 mm 左右的裂纹作为轮槽试样的裂纹萌生寿命。图6(a)给出的是试验现场照片。试验中发现，轮槽齿根A处(最大应力集中部位)最先萌生疲劳裂纹，这与有限元应力分析结果完全对应。图6(b)为某轮槽构件的裂纹观察情况。表3列出了各级载荷下的裂纹萌生寿命及对应的裂纹长度。

图5 基于背应力塑性功累积的轮槽构件寿命预测流程图Fig.5 Flow chart of the life prediction of rotor groove components based on the back stress plastic work accumulation

图6 轮槽构件低周疲劳试验现场照片(a)及裂纹观察(b)Fig.6 (a)Low cycle fatigue test site of wheel groove member；(b)observation of crack

表3 各级载荷下轮槽构件疲劳裂纹萌生寿命及对应的裂纹长度Table 3 Fatigue crack initiation life and corresponding crack length of the rotor groove components subjected to different loading levels

3.4 预测寿命与试验结果比较

采用建立的背应力塑性功能量模型进行轮槽构件疲劳寿命预测所得结果列于表4中，表中也给出了相应的试验寿命值及基于传统总应变能模型的寿命预测结果。图7是轮槽构件寿命预测结果与试验结果的比较。从图中可以清楚地看出：相比于总应变能寿命预测模型，基于背应力塑性功累积的寿命预测模型显著提高了轮槽构件的疲劳寿命预测精度，全部预测结果位于1.5倍分散带内。而基于总应变能的寿命预测方法得到相对保守的结果。由此证明了背应力塑性功累积更能反映材料疲劳损伤的本质，因此，建立的疲劳寿命预测能量模型值得工程疲劳设计重视。

表4 转子轮槽构件的寿命预测结果及其试验寿命值Table 4 Predicted and measured fatigue life of the rotor groove components

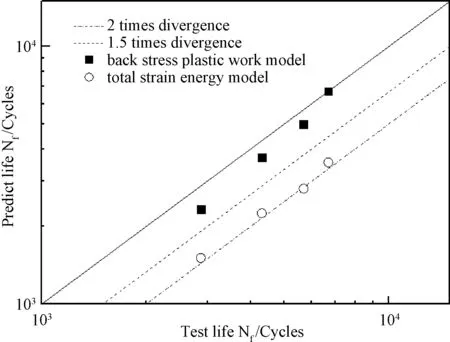
图7 轮槽构件预测寿命与试验寿命的比较Fig.7 Comparison of the predicted life and measured life of the rotor groove components

4 结 论

1.基于局部应力-应变法与疲劳损伤能耗结构，以疲劳过程中背应力塑性功累积为基础，并考虑缺口根部平均应力循环松弛行为，建立了一种新的缺口构件低周疲劳寿命预测能量模型。

2.针对某汽轮机轮槽构件，分别采用上述基于背应力塑性功的能量模型和传统总应变能量模型进行了低周疲劳寿命预测，并与试验寿命进行了比较。结果表明：基于背应力塑性功累积的能量模型能够显著提高轮槽构件的寿命预测精度，与试验寿命的误差小于1.5倍分散带，而基于总应变能的寿命预测值明显偏于保守。因此，本研究所建立的疲劳寿命预测能量模型值得工程疲劳设计者重视。