考虑动态输送容量机制的电力传输线过载风险评估

丁肇豪，余开媛，王 程

（华北电力大学电气与电子工程学院，北京市102206）

0 引言

风光等可再生能源大规模接入电网不仅给电力系统运行灵活性带来挑战，同时对输电线路输送容量提出更高要求。一般而言，电力传输线的输送容量取决于最大载流量，其数值依赖其最高允许运行温度及环境参数。在中国，整定电力传输线输送容量时采用了较为保守的环境参数［1］，导致很多场景下线路容量被低估。文献［2］研究表明，传输线输送容量与环境风速在一定范围内呈正相关，换言之，风电场外送传输线允许的实际输送容量可能远高于该线路的整定输送容量。若使用环境参数动态或实时整定输送容量以反映传输线功率实际上限，可有效降低电网建设及调度运行成本，此即动态输送容量（dynamic line rating，DLR）机制［3-4］。

DLR 技术并非新生事物，国内外已有不少相关研究和应用案例。文献［5］总结了各种DLR 技术。文献［6］提出架空线路DLR 的通用计算模型并将其应用至含大规模风电的电力系统运行优化问题；文献［7］考虑架空输电线路的动态载流量计算方法；文献［8］开发了一种基于实时天气预报的DLR 测量算法，可为调度中心提供长达2 d 的输送容量预报。在理想DLR 模型中，可以基于采集数据计算实时载流量，并将其应用于电力传输线，实现容量充分优化。应当指出，传输线DLR 的准确整定依赖于精确的环境参数。然而，类似于风光电站出力，传输线附近环境参数在电网多时段调度过程中无法精确获知，只能按照其预测值整定传输线输送容量，故应用DLR 技术评估得到的传输线输送功率上限具有较强不确定性［9］。若对传输线输送功率上限估计过于乐观，可能导致线路过载，严重的甚至引发电网连锁故障，因此需要考虑DLR 不确定性对电力系统运行的负面影响。文献［10］构建了考虑传输线DLR 的鲁棒调度模型，采用盒式不确定集合对传输线输送容量不确定性进行建模。文献［11］立足于风电出力与传输线DLR 之间的相关性，以数据驱动的模糊集对上述不确定性进行建模。然而，以上工作虽然在量化DLR 不确定性对电力系统运行的影响方面已经做了大量的研究，但是并未提供传输线输送容量最大允许偏差，由DLR 不确定性引起的输电线路过载风险评估仍是一个悬而未决的问题，进而无法为电力调度中规避传输线过载风险提供指导。

国内外学者在风光不确定性引发的弃风、弃光风险方面已开展不少研究，可为传输线过载风险管理所借鉴。文献［12］基于改进等分散抽样蒙特卡洛法，量化大规模风电并网背景下的交直流混联系统运行风险。文献［13］构建了概率区间优化模型评估短时间内风电的消纳情况，以此计算风电功率预测误差引入的电网运行风险。文献［14］基于非支配排序遗传算法（NSGA）的多目标优化方法，采用级联过载指标在线优化与过载相关的系统安全指标，评估潮流最优分布时传输线的过载风险，然而其并未对线路DLR 机制进行建模。

本文针对考虑DLR 机制的电力系统运行问题，将气象因素引起的传输线输送容量不确定性以盒式集合表述，提出传输线过载风险指标，构建基于两阶段鲁棒优化的传输线过载风险评估模型，得到DLR不确定性引起的输电线路过载风险以及各条传输线输送容量最大允许偏差，进而为电力调度中规避过载风险提供指导。模型采用列与约束生成（columnand-constraint generation，C&CG）［15-17］算法进行高效求解，最后在测试系统中验证所提模型及求解算法的有效性。

1 模型建立

1.1 考虑DLR 机制的传输线过载判据

本文提出一种考虑传输线输送容量极端场景的传输线过载判据，即假设传输线输送容量不确定，旨在极大化电力系统运行再调度阶段线路过载量，其数学上表现为双层max-min 形式，如式（1）所示。

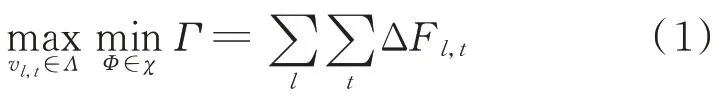
式中：ΔFl，t为t 时段传输线l 的过载量；vl，t为t 时段传输线l 的输送容量不确定性，为布尔变量，取1 和0分别表示传输线容量达到其不确定区间下限和不确定区间预测值；Λ 为传输线输送容量不确定性集合，最坏场景下的输送容量如式（2）所示；Φ={ pg，t，pl，t，θn，t，ΔFl，t}表示min 问题的决策变量集合，其中pg，t为t 时段发电机组g 的出力值，pl，t为t 时段传输线l 的传输功率，θn，t为t 时段节点n 的相角；χ 为Φ 中决策变量的可行域，包括约束式（3）—式（10）。

1）发电机组出力约束

2）发电机组爬坡约束

3）参考节点相角约束

式（6）表示t 时段参考节点相角θref，t为零。

4）基于直流潮流的线路潮流

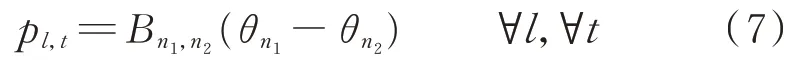
5）电力系统节点平衡约束

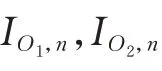
6）传输线容量约束

应当指出，由于式（1）中传输线过载量恒非负，因此，将求解得到的最优值作为本问题中传输线过载判据。具体地，若Γ=0，则表明当前传输线容量不确定集合内的任意场景均不会造成过载损失；反之，若Γ ＞0，则表明在当前传输线容量不确定集合内存在场景使得电力系统产生过载损失。

1.2 传输线过载风险评估模型

本节提出一种传输线过载风险指标，其示意图如图1 所示。

图1 传输线过载风险示意图Fig.1 Schematic diagram of overload risk for transmission line

式中：L 为线路条数；T 为总时段数；cl为传输线l 的过载罚系数；Fl，t为t 时段传输线l 的静态输送容量；Pr(δl，t)表示输送容量预测误差的概率分布函数。

本文综合考虑后将Risk作为定值进行处理。式（11）中被积函数为传输线输送容量最大允许偏差与传输线实际输送容量的差值。应当指出，由于传输线容量不确定性的预测误差的概率分布难以精确获得且积分计算较为困难，为此采用分段线性化方法对式（11）进行处理，从而构建计算友好的传输线过载风险评估模型，即

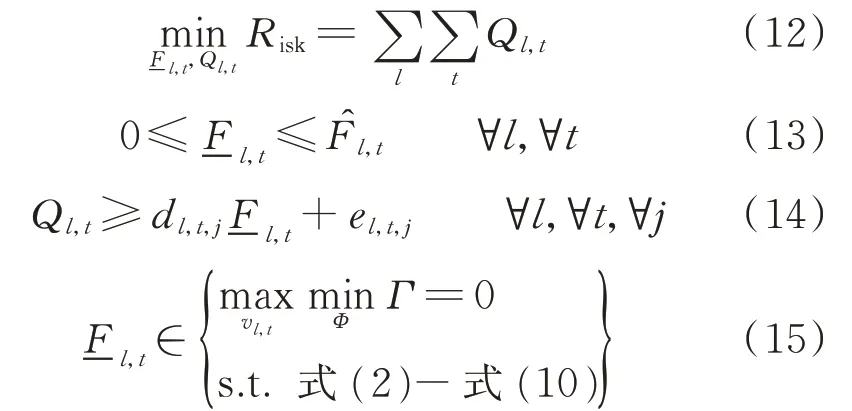
式中：Ql，t为t 时段传输线l 的过载风险；dl，t，j和el，t，j为t 时段传输线l 的风险线性化各分段系数，j 表示分段系数编号。

该模型实际上构成一种两阶段优化模型。式（12）—式（14）为模型第1 阶段，旨在通过调整各条传输线在各时段不产生过载损失对应的传输线输送容量下限，降低整体过载风险。其中，式（13）为考虑DLR 机制的传输线容量范围，式（14）为线性化运行风险指标增加的辅助约束。第2 阶段由式（15）所示传输线过载判据构成，其中要求最优值Γ=0。通过求解该两阶段优化模型，即可得到传输线输送容量最大允许偏差及对应过载风险。

2 模型求解

2.1 模型等价转换

如前文所述，本文所提考虑DLR 机制的传输线过载风险评估模型在数学上属于一种两阶段优化模型，第1 阶段以式（12）为目标函数，以式（13）—式（15）为约束构成评估主问题；第2 阶段以式（1）为目标函数，以式（2）—式（10）为约束构成传输线过载判别子问题。

1）求解传输线过载判别子问题

式中：Q，R，S，T，U，B，r，u 为传输线过载判别子问题的常系数矩阵或向量；v 为DLR 不确定性的布尔型向量，取1 表示传输线容量达到其不确定区间下限，取0 表示传输线容量达到其不确定区间预测值；c 为DLR 可接纳边界的连续性向量；Pg，Pl，θ，ΔF 分别为发电机出力值、传输线传输功率、节点相角值以及在最坏情况下传输线过载量；“∘”表示Hadamard 积。

不难看出，传输线过载判别子问题是一个双层混合整数线性规划问题，且内层min 问题为线性规划。因此，可采用Karush-Kuhn-Tucker（KKT）最优性条件或强对偶定理［18］将其等价转化为单层混合整数线性规划问题。本文采用强对偶定理得到内层min 问题的对偶问题，进一步与外层max 问题合并，可得判别子问题的等价形式如下。

式中：ζ 为对偶变量，注意到式（18）中存在双线性项，为此继续引入中间变量，添加相应的辅助约束，等价转化如下。

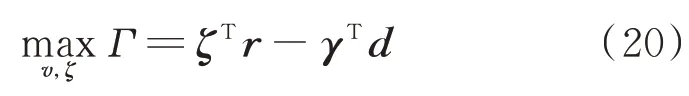
式中：d 为常数向量；M 为一个足够大的常数，在实际求解的过程中可以根据不同的参数灵活地进行数值的选择。经过以上转化，模型中的子问题转变成一个单层混合整数线性规划问题，可由商业求解器Gurobi 对其进行求解。

2）输出传输线输送容量最大允许偏差

式中：D，E，rs为常系数矩阵或向量；q 为系统过载风险向量。

2.2 求解算法

本文构建的传输线过载风险评估两阶段优化问题的主问题、子问题均为易于求解的线性规划或混合整数线性规划问题。一般而言，两阶段优化模型可调用Benders 分解算法［19］和C&CG 算法高效求解，与Benders 分解算法相比，后者采用统一解法处理最优性和可行性问题，其执行速度比Benders 分解算法快［20］。故此处采用C&CG 算法求解，其主要步骤如下。

步骤1：设置迭代次数k=0，收敛误差ε。

步骤3：求解由式（20）—式（21）构成的传输线过载判别子问题。其中，记v 的最优解为v(k+1)，目标函数Γ 的最优值为Γ(k+1)，若Γ(k+1)＜ε，则终止算法并输出c(k)；否则，增加向量及相应约束至第1 阶段主问题。

步骤4：令k=k+1，返回步骤2。

3 算例测试

本文采用IEEE 5 节点、24 节点和118 节点电力系统为测试算例，分别记作测试系统Ⅰ、Ⅱ、Ⅲ，对本文所提模型进行测试。测试系统Ⅰ、Ⅱ的算例拓扑结构分别见图2 和图3，详细参数见文献［21］。

图2 测试系统Ⅰ的拓扑图Fig.2 Topology of test system Ⅰ

图3 测试系统Ⅱ的拓扑图Fig.3 Topology of test system Ⅱ

3.1 应用DLR 机制的传输线条数对结果的影响

系统运行成本为应用DLR 机制时的发电成本。应用DLR 机制后，传输线容量一般高于其静态值，有望缓解电力系统阻塞现象，进而降低系统运行成本。由于DLR 固有的不确定性，应用该机制可能引入额外的过载风险。本节将使用测试系统Ⅰ分析采用DLR 机制的传输线条数对系统运行的影响。其中，边际净收益表示当DLR 机制的传输线集合变化时，系统运行成本降幅与过载风险增幅的差值。测试编号为1～6，其中应用DLR 机制的传输线条数为1～6，具体传输线编号及仿真结果见表1。如无说明，后文中传输线输送容量基准值均为100 MW。

表1 传输线条数对评估结果的影响Table 1 Impact of number of transmission lines on evaluation results

由表1 可知，传输线过载风险随着应用DLR 机制的传输线条数的增加而增加，而系统运行成本则逐渐降低。进一步，系统边际净收益的值并非随应用DLR 机制的传输线条数单调增加。在测试5 中，应用DLR 机制为系统带来的边际净收益最大，而在测试2 中，边际净收益为负值，即此时应用DLR 机制传输线条数的增加会恶化系统的运行情况。综上可知，在实际应用中需要整定应用DLR 机制的传输线条数及具体编号，从而最大化DLR 机制给系统运行带来的净收益。

3.2 机组组合对结果的影响

为测试机组组合对传输线过载风险的影响，在测试系统Ⅱ中设置不同的机组组合方案，共4 组工况：①机组全部开机；②发电机G1关闭；③发电机G2关闭；④发电机G1和G2均关闭。测试编号为7～10。机组开停机对系统过载风险的影响见表2。

表2 机组开停机对系统过载风险的影响Table 2 Impact of unit on-off system overload risk

由表2 可知，测试7 的传输线过载风险明显低于测试8 至测试10，说明机组停机会导致电力系统过载风险增大。当部分机组停机时，其余机组的发电功率将会增大，可能导致传输线潮流分布较为集中，进而增大传输线过载风险；当机组全部处于开机状态时，传输线潮流分布将更为灵活分散，可最大程度避免部分传输线功率过高，使得传输线过载风险最小。改变机组组合方式后电力系统运行风险有所改变，能够真实反映电力系统传输线的过载风险，与工程实际相符。

在测试系统Ⅱ找出不同的传输线（图3 中彩色部分），在4 组测试工况下传输线输送容量零过载下限如图4 所示。传输线输送容量零过载下限表示在零过载损失前提下传输线输送容量的最小值。若某种机组组合方案下传输线输送容量实际值低于图4中对应曲线，则该条传输线将产生过载损失。事实上，图4 中各条曲线到其静态输送容量的距离，即为式（11）中传输线过载风险积分距离。换言之，曲线某时刻偏离x 轴的程度越高，则该条传输线此时刻的过载风险越大。

由图4 可知，测试7 对应机组组合方案得到的传输线输送容量零过载下限在所测试的传输线中均为全局最小，因此该方案对应的传输线过载风险也最小。而测试9 和测试10 的传输线输送容量零过载下限分别在几条传输线中为全局最大，导致其对应的传输线过载风险远高于测试7 和测试8。综上，发电机机组开停机会影响传输线过载风险评估结果，合理制定机组启停计划对抑制由DLR 不确定性引发的传输线过载风险具有重要意义。

图4 机组开停机方式对传输线输送容量零过载下限的影响Fig.4 Impact of unit on-ff mode on the lower limit of zero overload of ampere capacity for transmission line

3.3 系统规模对求解效率的影响

为测试系统规模对本文提出的传输线过载风险评估方法求解效率的影响，采用测试系统Ⅲ为算例进行测试，测试结果如图5 所示。

图5 系统规模对求解效率的影响Fig.5 Impact of system scale on solving efficiency

图5 中，时段数与应用传输线DLR 机制的传输线条数均直接影响系统规模。不难看出，当系统规模增大时，计算时间总体呈现增长的趋势。其原因在于，当应用传输线DLR 机制的传输线条数增加时，第2 阶段传输线过载判别子问题中不确定集合的规模增大，其等价的单层优化问题中布尔型变量的个数及含大M 的约束个数均增大，辨识最优策略需要花费更多时间。同时，当时段数变化时，求解时间并无固定变化趋势，体现为无规则波动。应当指出，在各组测试下IEEE 118 节点系统求解时间不超过307 s，在实际应用时，根据需要对应用DLR 机制的传输线条数和具体编号进行合理的调整，兼顾计算用时和系统效率。

4 结语

在传输线DLR 机制中，传输线容量的整定结果与其周围气象条件的预测精度直接相关，使得此机制下动态整定获得的传输线容量天然具有不确定性。为此，本文提出了一种考虑传输线输送容量不确定性的过载风险评估模型，旨在评估电力系统因应用DLR 机制而产生的过载风险，并求解总过载风险最小条件下各传输线潮流分布的最优方案。本文提出的模型数学上属于两阶段鲁棒优化范畴，故采用较为成熟的C&CG 算法求解。本文探究了机组开停机方式、应用DLR 机制的传输线条数对最终评估结果的影响，所提模型及算法在IEEE 118 节点测试系统的求解效率体现了其在工程实际的推广意义。对于未来的研究有各种开放性问题值得考虑，例如，提出的模型如何考虑其他不确定性来源，如何充分处理作为导体动态行为函数纠正措施的时间等等。在未来将风电或光伏纳入考虑的范围，也将会是该模型很好的扩展方向。