自储能柔性互联配电网多时间尺度电压优化

2021-05-07褚国伟张友旺万立新

电力系统自动化 2021年9期

褚国伟，张友旺，葛乐，万立新

（1. 国网江苏省电力有限公司常州供电分公司，江苏省常州市213003；2. 南京工程学院电力工程学院，江苏省南京市211167）

0 引言

现代配电网的阻抗比大，电压对有功和无功的变化均比较敏感，传统调压设备难以根本解决高渗透率分布式电源（distributed generator，DG）引起的电压越限问题［1-2］。

智能软开关［3-11］、背靠背柔性直流［12］、直流链路［13］和能量路由器［14-15］等配电网柔性互联设备具有相似的拓扑结构，可实现馈线间功率“交-直-交”解耦传输、潮流精准控制、动态无功补偿和供电方式灵活无缝切换等功能。但互联馈线的可调节容量往往制约其优化控制的效果，极端时甚至不能满足安全性要求。自储能多端背靠背柔性直流（self-energy storage based multi-terminal back-to-back voltage source converter based high voltage direct current，SESDC）装置［16-18］因同时具备了时间和空间2 个层面的灵活控制能力，相对于分散独立配置储能和柔性互联设备，其具有更小的体积和更低的成本，同时，也降低了电网通信调度的复杂度，为配电网电压调节与优化提供了一种新的技术路线。

目前，国内外已对柔性互联设备参与配电网调压进行了一定研究。文献［3］建立了柔性互联设备电压无功控制的时序模型；文献［4-5］分别提出了灵敏度系数和多目标自适应优化的调压方法，但未涉及与传统调压设备的协调；文献［6-7］分别构建了协调传统调压设备和柔性互联设备的时序电压优化和电压双层优化模型。考虑到分布式电源功率突变引起的电压越限时长一般小于预测时长［19］，因此，优化模型需要引入实时调节环节。为降低实时控制对配电网通信和计算性能的要求，文献［8］提出了基于多智能体的分布式自适应控制；文献［9-10］提出了基于电压-无功下垂曲线的就地电压控制。在对求解算法进一步优化的基础上，实时集中控制未来也可应用到自动化水平较高的配电网。

储能的引入给多时间尺度电压优化模型带来了新的挑战。储能荷电量具有时序上的绝对连续性，日前优化可以给出储能全时段最优充放电策略，但日前DG 负荷预测会存在一定偏差，储能日前最优出力不能直接用于日内控制。日内优化是基于超短期预测的单时间断面最优控制，其求得的储能最优出力无法实现全时段最优，甚至会出现部分时段因过充或过放失去调节能力的问题。因此，本文首先需要解决集成储能模型中不同时间尺度优化间的协调问题。

传统调压设备挡位的离散性和储能电量的时序连续性决定了电压优化模型是多时段强耦合的混合整数非凸、非线性问题。混合整数的连续多时段耦合问题可通过动态规划算法［19］求解，而非凸、非线性的模型可转化为二阶锥规划（second-order cone programming，SOCP）［4，6，11］求解。SOCP 是有限个线性和锥约束下的线性目标优化算法，而相同条件下的线性约束会比锥约束求解效率高，为提高求解效率，有必要对锥约束进行线性松弛。

1 SESDC 的“时-空”电能调节特性

SESDC 将多个DC/AC 换流器和储能DC/DC换流器的直流侧并联在公共直流母线上，交流侧与配电网馈线相连。各换流器在其自身容量约束下，控制各端口的无功功率，同时在馈线容量约束下，控制各端口的有功功率，从而实现配电网的柔性互联运行。储能的加入使得交流馈线间不再要求功率实时平衡。

SESDC 中储能电量的时序绝对连续性构成了电能的时序耦合关系，如式（1）所示。同时，SESDC各端口有功功率之和为零，由此构成了电能的空间耦合关系，如式（2）所示。储能有容量和功率的限制，各换流器的功率虽可解耦控制，但仍需满足端口容量限制，如式（3）所示。式（1）至式（3）组成了SESDC 的“时-空”电能调节特性。

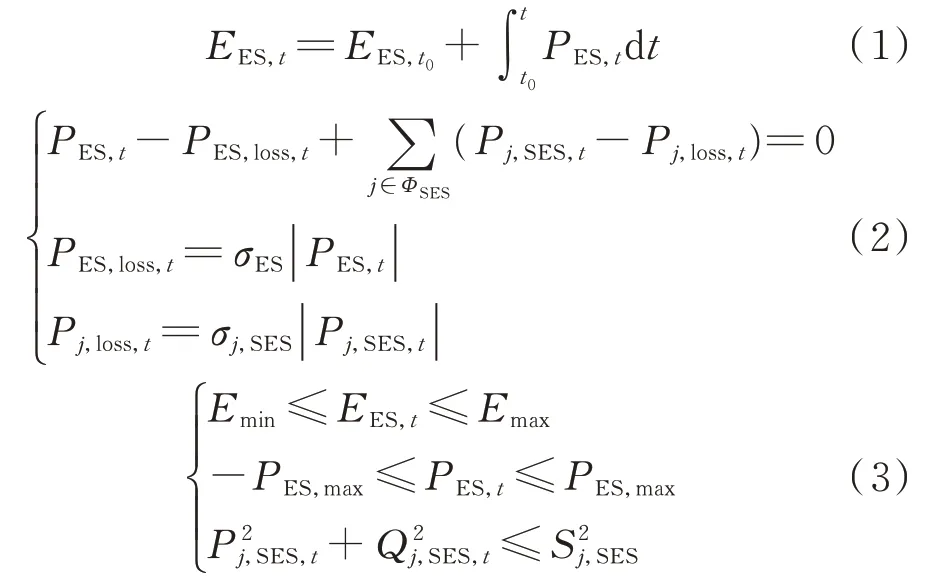
式中：EES，t为时段t 储能的电量；EES，t0为储能的初始电量；PES，t和PES，loss，t分别为时段t 储能的调度功率和损耗功率；σES为储能损耗系数；ΦSES为SESDC 各柔性直流（以下简称“柔直”）端口与馈线相连节点的集合；Pj，SES，t和Pj，loss，t分别为时段t 与节点j 相连柔直端口调度功率和损耗功率；σj，SES为与节点j 相连柔直端口损耗系数；Emax和Emin分别为储能电量的安全上、下限；PES，max为储能额定功率；Qj，SES，t和Sj，SES分别为时段t 与节点j 相连柔直端口输出的无功功率和相应的换流器容量。

2 多时间尺度协调电压优化模型

多时间尺度协调电压优化模型由日前优化、日内优化和实时调节3 个阶段组成。这3 个阶段相互联系，解决SESDC 与传统调压设备协调、储能电量连续性与日内单时间断面优化不相适应以及DG 出力突变引起的电压短时越限等问题。

日前电压优化基于DG 和负荷的日前预测曲线，以全时段电压偏差和网损最小为控制目标，以有载调压变压器（on-load tap changer，OLTC）和电容器组（capacitor bank，CB）挡位以及SESDC 各柔直和储能端口出力作为控制变量建立优化模型。主要任务是确定日内运行中OLTC 和CB 挡位等离散量的优化方案，并为日内优化提供各时段的储能出力取值区间。

日内电压优化的主要任务是以单个时间断面循环滚动的方式求解装置在各时段的运行策略。基于日前优化传递的OLTC 和CB 挡位及储能功率取值区间，以SESDC 各端口出力作为控制变量，以当前时段电压偏差和网损最小为目标构建优化模型，求解当前时段的电压-功率灵敏度矩阵，并更新储能功率限制区间，传递到实时优化阶段。

考虑到中国配电自动化发展的现状，实时调节给出了集中全局优化和就地控制2 种方案。对于自动化水平较高的配电网，以光纤通信的方式实时上传敏感节点的电压越限信息，集中控制依据电压-功率灵敏度矩阵计算出DG 功率变化量，以网损和电压偏差最小为优化目标，实时调节SESDC 中各端口输出功率。除了通信的快速性可靠性要求以外，集中控制要求更快的决策计算速度，本文针对性地进行了算法改进。针对自动化水平较弱的配电网，就地控制不依赖通信，基于本地采集的电气量通过电压-功率灵敏度矩阵直接计算出相应端口的调节量。

基于上述分析，自储能柔性互联配电网多时间尺度协调电压优化框架如图1 所示。

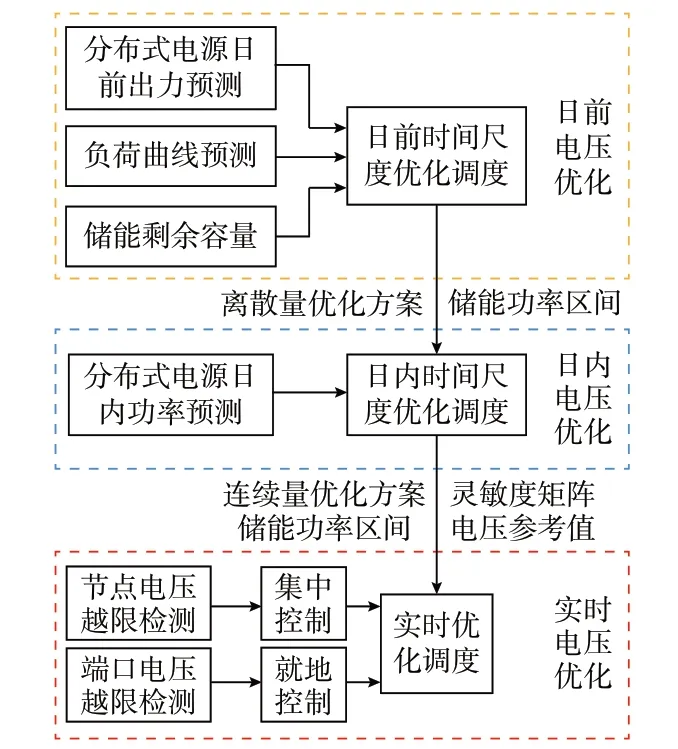
图1 多时间尺度协调电压优化框架Fig.1 Multi-time scale coordinated voltage optimization framework

2.1 日前电压优化模型

2.1.1 目标函数

为保证配电系统运行安全性和经济性，日前电压优化以下一日全时段电压偏差和网损最小为优化目标。目标权重由2 个部分组成，层次分析法确定主观权重［3，6，9］，并根据系统当前运行状态确定客观适应性权重［5］。此外，考虑到节点电压偏差量与DG位置、DG 输出功率和该节点与馈线首端的电气距离等因素［5］，在电压偏差目标中，依据上述因素设定单一节点的电压偏差权重。设置每个时段为15 min，即每日有96 个时段，优化目标为：

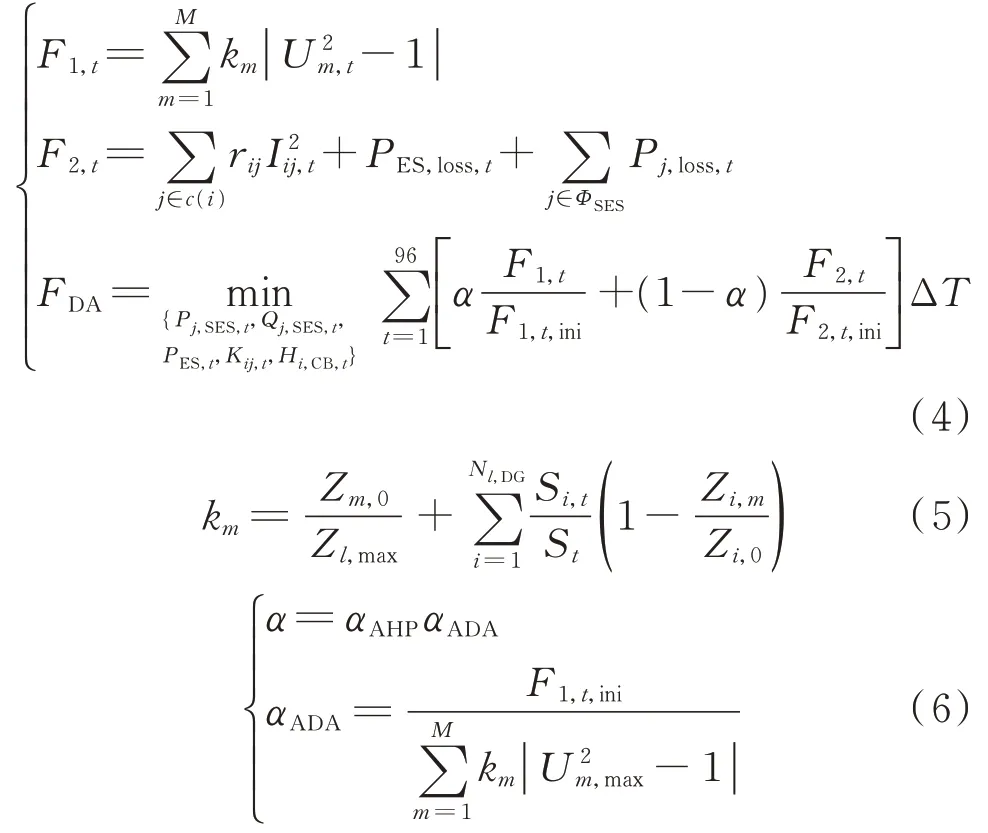
式中：F1，t和F2，t分别为时段t 电压偏差量和网损量；M 为系统总节点数；km为节点m 的电压偏差权重；Um，t为时段t 节点m 的电压；c(i)为以节点i 为首端节点的所有支路的末端节点集合；rij为支路ij 的电阻；Iij，t为时段t 支路ij 的电流；FDA为日前目标函数；Kij，t为支路ij 处OLTC 在时段t 的可调挡位；Hi，CB，t为节点i 处CB 在时段t 的可调挡位；α 为综合权重，取值越大，对电压要求越高，电压偏差越小，电网安全性越强，相反的，取值越小，网损越小，电网运行经济性越好；F1，t，ini和F2，t，ini分别为时段t 未经优化的电压偏差和网损值；ΔT 为时间间隔；Zm，0为节点m 到馈线首端的阻抗；Zl，max为馈线l 首末端最大阻抗；Nl，DG为节点所在馈线l 上DG 的个数；Si，t为第i 个DG 在时段t 的输出功率；St为时段t 馈线的总负荷量；Zi，m为第i 个DG 到节点m 的阻抗；Zi，0为第i 个DG 到馈线首端的阻抗，当Zi，m＞Zi，0时，修正Zi，m=Zi，0；αAHP为层次分析法权重；αADA为适应性权重，与未经优化的电压偏差量成正比，电压偏差量越大，权重越大；Um，max为节点电压幅值上限。

2.1.2 约束条件

日前优化模型的约束条件包括潮流约束、电压约束、OLTC 或CB 的运行约束和动作次数约束等，这方面内容可参考文献［4-8，20］，具体表达式如附录A 式（A1）至式（A6）所示。

SESDC 日前优化还需保证一天的始末时刻储能电量相同，结合式（1）至式（3）可得SESDC 的运行约束为：

式中：EES，96为储能在第96 个时段结束时的电量。

如前文所述，日前优化结果不能直接用于日内的储能控制，而单纯日内优化得到的储能功率又不满足全时段最优要求。因此，通过式（8）给出日内储能功率的取值区间限制，即在额定功率的约束下，以日前储能优化功率为区间中点，一定的区间宽度形成的区间。

式中：PES，max，t和PES，min，t分别为日内优化阶段SESDC 储能功率限制区间在时段t 的上、下限；L 为区间宽度，L=μPES，max，其中，μ 为区间宽度系数，可以通过多次试验获得。

日前优化求得Kij，t、Hi，CB，t和储能功率区间[ PES，min，t，PES，max，t]，以此为基础进行日内优化。

2.2 日内电压优化模型

日内优化以DG 预测出力Pj，DG，t、储能功率区间[ PES，min，t，PES，max，t]、日前优化传递的Kij，t和Hi，CB，t共同作为已知参数，以储能及各柔直端口输出功率作为控制变量，以当前时段电压偏差和网损最小为目标构建优化模型的目标函数FID如式（9）所示，约束条件为：式（1）—式（3）、式（5）、式（6）、附录A式（A1）和式（A6）。

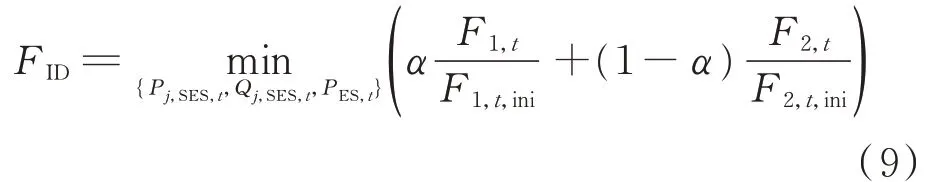
日内优化求得各时段PES，t、Pj，SES，t和Qj，SES，t，由此确定各时段系统运行状态。

DG 极短时的功率突变往往无法预测，基于DG超短期预测的日内优化难以处理DG 出力突变引起的电压越限问题，因此，需要进一步引入实时调节。日内优化通过式（10）求出当前时段各节点的电压-功率灵敏度矩阵，并依据日内当前时段储能功率更新式（8）的储能功率限制区间，传递至实时调节阶段。

式中：ΔUj为节点j 的电压变化量；ΔPj和ΔQj分别为节点j 的有功和无功变化量；∂Uj/∂Pj和∂Uj/∂Qj分别为节点j 的电压-有功功率灵敏度和电压-无功功率灵敏度。

2.3 实时电压调节

实时电压调节仅在DG 功率突变等造成节点电压越限时启动。对于通信自动化水平较高的配电网，采用集中全局优化方案：在线检测DG 并网点、馈线末端节点等敏感节点［5］的电压，在越限发生时，实时上传各关键节点电压越限信息。依据节点j 的电压实测值Uj，DG和日内传递的电压-功率灵敏度矩阵，通过式（11）计算出节点j 的DG 有功功率变化量ΔPj，DG。

式中：Pj，DG为节点j 的DG 有功功率；Uj，DG，ref为DG在节点j 的参考电压值。

将DG 功率变化量与该时段的日内预测量叠加，作为实时DG 出力。以电压偏差和网损最小为目标构建式（12）所示优化模型，约束条件为：式(1)—式(3)、式(5)、式(6)、附录A 式（A1）和式（A6）。

式中：FRT为日内实时目标函数。

对于通信自动化水平相对较低的配电网，采用就地控制模式：就地检测SESDC 各端口电压，得到节点j 的端口电压值Uj，SES。当端口电压越限时，首先依据所在端口的电压-功率灵敏度矩阵计算出各端口无功偏差量，如式（13）所示，判断是否满足式（3）中换流器容量限制。若满足，即换流器无功可调容量充足，直接将其叠加到柔直端口的无功控制指令上；若不满足，在无功调节的基础上，调节换流器有功功率输出［21］，以满足系统的电压调节需求，如式（14）所示。调节过程需要满足式（1）—式（3）的SESDC 电能调节特性的约束。

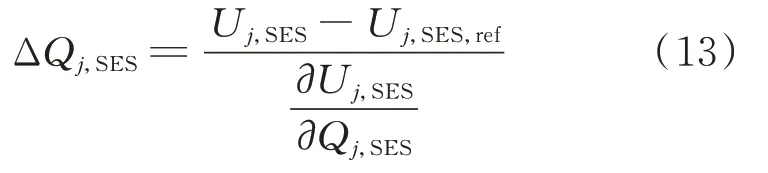
式中：ΔQj，SES和ΔPj，SES分别为与节点j 相连的柔直端口的无功和有功功率偏差量；Qj，SES和Pj，SES分别为与节点j 相连的柔直端口的无功功率和有功功率；Uj，SES，ref为与节点j 相连的柔直端口参考电压值。

3 模型处理与求解

上述多时间尺度电压优化模型，日前优化中含有储能电量的时序限制，并且包含换流器输出功率的限制，由此造成了时间、空间的强耦合。同时，模型中既有传统调压设备动作时刻和挡位的离散变量，又有SESDC 输出功率值的连续变量，属于多时段强耦合的混合整数非凸、非线性优化问题，难以直接求出最优解。为此，设计双层求解算法，上层处理多时段耦合的混合整数优化问题，采用动态规划法求解；下层处理空间耦合的问题，即最优潮流的分布，为提高计算效率，采用多面体松弛技术改进二阶锥规划（polyhedron relaxed second-order cone programming，PR-SOCP）求解。日内和实时优化只需要在日前优化的基础上计算当前时段和时间点的最优潮流问题，不需要进行全时段的动态规划求解，相当于日前优化的简化过程。

3.1 上层求解算法

动态规划是求解多阶段决策过程最优化的有效算法之一［19，22］，依据最优性原理将问题细化为子策略最优并迭代求解，任意阶段的最优决策均从全局出发，而不仅限于当前阶段的最优。主要包括以下4 个步骤。

步骤1：划分时段。将一天划分为96 个时段，相邻时段相差15 min。

步骤2：确定状态和决策。状态包括SESDC 中储能剩余电量EES，t、OLTC 挡位Kij，t和CB 挡位Hi，CB，t，通过电量差ΔE 将储能电量EES，t离散化；对应状态为储能充放电功率PES，t、OLTC 调节步长Δkij和CB 调节步长ΔQi，CB。

步骤3：列写状态转移方程和指标函数。储能的状态转移方程即为剩余电量与充放电功率关系方程，如式（1）所示。OLTC 和CB 的状态转移方程为对应挡位关系，如附录A 式（A4）和式（A11）所示。式（4）为总指标函数，时段t 的指标函数为时段1 至时段T 的总目标函数，如式（15）所示。

步骤4：给定边界条件。运行边界条件为各类运行约束，如附录A 式（A1）至式（A6）和式（7）所示。

针对附录A 式（A4）至式（A6）中含OLTC 和CB 挡位的混合整数问题，将OLTC 和CB 挡位作为动态规划算法中的状态变量，将附录A 式（A4）和式（A5）作为其状态转移方程，式（A6）为动态规划算法的运行边界条件，通过动态规划算法处理包含OLTC 和CB 挡位等离散量的多阶段最优决策问题。

3.2 下层求解算法

3.2.1 优化模型转化为SOCP

首先，将模型进行二阶锥转化［4，6，11，23］，相关推导过程如附录B 所示。

通过二阶锥松弛、目标函数线性化、约束条件变为线性和二阶锥约束，模型转化为SOCP。相同条件下的线性约束会比二阶锥约束求解效率高，因此，利用多面体松弛技术［24］对SOCP 中的二阶锥约束进行线性松弛，进而转化为线性规划求解。

3.2.2 PR-SOCP

以附录B 式（B7）的二阶锥约束为例，可引入一组变量P0，P1，…，Pk，Q0，Q1，…，Qk，通过多面体松弛线性表示为：

式中：1≤i ≤k。

式（16）中的等式可用于消去变量X1，X2，…，Xk，二阶锥约束的线性不等式表示如附录B 式（B7）所示。

对于附录B 式（B6）所述四维二阶锥，可引入中间变量ρ，再将其线性化，等效表示为：

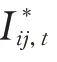
至此，所有二阶锥约束均已线性表示，原SOCP问题通过PR-SOCP 转化为线性规划问题。可直接通过MATLAB 调用YALMIP 工具箱和CPLEX求解。

4 算例分析

4.1 算例设置

本文选用中国华东某地区四端柔性互联配电系统作为测试算例，系统共有72 个节点，结构如图2所示。图中PV 表示光伏发电单元；WT 表示风电机组；ESS 表示储能系统。系统支路参数、DG 配置参数如附录C 表C1 和表C2 所示。考虑到DG 日前预测误差一般在20%以内，日内15 min 超短期预测误差在5%以内［25］，设计场景1 和场景2，其日前预测误差分别为20%和10%，DG 预测和负荷数据如附录C 图C1 所示。场景1 包括2 个DG 实时输出功率突变情况：13：15 时，馈线D 节点72 的光伏脱机；18：00 时，馈线A 节点27 的风电输出功率减小了50%。

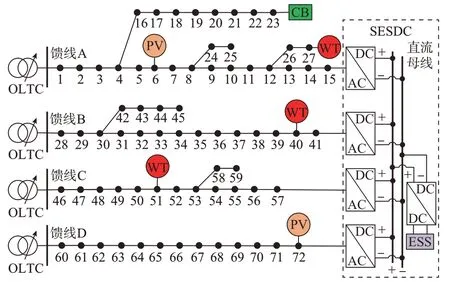
图2 四端柔性互联配电系统结构Fig.2 Structure of the four-terminal flexible interconnected distribution system

四端馈线首端分别装设有一台OLTC（副边额定电压为10.5 kV）；馈线末端分别在节点15、41、57和72 处，与SESDC 的柔直端口相连，各端口额定容量均为2 MVA，综合损耗系数为4%（包括电能变换损耗和设备散热等综合损耗）；储能为锂离子电池，额定功率为1 MW，额定电池容量为4 MW·h，综合损耗系数为9.76%（包括本体、变流器、隔离变和散热等损耗），初始电量为0.2 MW·h，电量上、下限分别为3.8 MW·h 和0.2 MW·h；参考文献［19］，电量差设置越小，动态规划求解精度越高但计算耗时更长。考虑到实际配电网的计算规模，为了权衡求解精度与计算时间，将电量差ΔE 设为0.1 MW×15 min。节点23 设有2×50 kvar 的CB。设置每日OLTC 最大动作次数为6，CB 投切和储能充放电状态转换最大次数为4。应用层次分析法［3，6，9］得出电压偏差目标函数的权重α 为0.75。仿真计算机配置情况：处理器型号为intel core i5 4200U，主频为1.6 GHz，内存为4 GB。

4.2 仿真结果及分析

4.2.1 SESDC 电压优化效果对比分析

为了验证本文提出的SESDC 参与配电网电压控制的效果，以场景1 为例，基于本文多时间尺度模型对采用3 种不同调节设备的优化方案进行对比分析。

方案1：配电网开环运行，等价于柔性互联装置不投入运行。

方案2：仅通过多端背靠背柔直实现柔性合环，等价于SESDC 中储能不参与调节。

方案3：通过SESDC 实现柔性合环。

日前优化求得各方案OLTC 挡位、CB 挡位和储能功率区间如附录D 图D1 至图D3 所示。

3 种方案所得日内各馈线96 时段电压偏差和网损数据如表1 所示，其中，电压偏差均为标幺值。各时段节点电压曲线如图3 所示，各时段网损如附录D 图D4 所示，设备损耗按馈线传输功率进行归算。

表1 系统电压偏差和网损Table 1 System voltage deviation and network loss

在电压调节方面，方案1 至方案3 的电压优化效果依次递增。方案1 平均电压偏差量最大，馈线A和B 中，电压偏差最大值超过0.1，已严重影响DG并网和系统安全运行。这充分说明“闭环设计、开环运行”的传统配电网对新能源的消纳能力有限。方案2 没有储能参与调节，系统在部分时段缺乏足够的有功调节能力，其中，馈线C 和D 的电压偏差相较于方案1 更大，原因在于互联装置吸收馈线C 和D有功功率用以支撑节点数多、负荷重的馈线A 和B的电压，影响了馈线C 和D 的电压。这说明柔性互联配电网的调节能力受馈线实际可调容量的影响，在部分时间段不足以维持系统的安全电压水平。方案3 相对于方案2 的电压偏差更小，并且无电压越限现象，说明引入储能后，系统的调节能力得到进一步加强。需要补充说明的是，对于方案2 和方案3，在全线电压水平和降低网损的双重作用下，各馈线的电压最高点往往出现在线路始端，而OLTC 的电压整定是离散控制，因此会出现各馈线始端电压相同的情况。

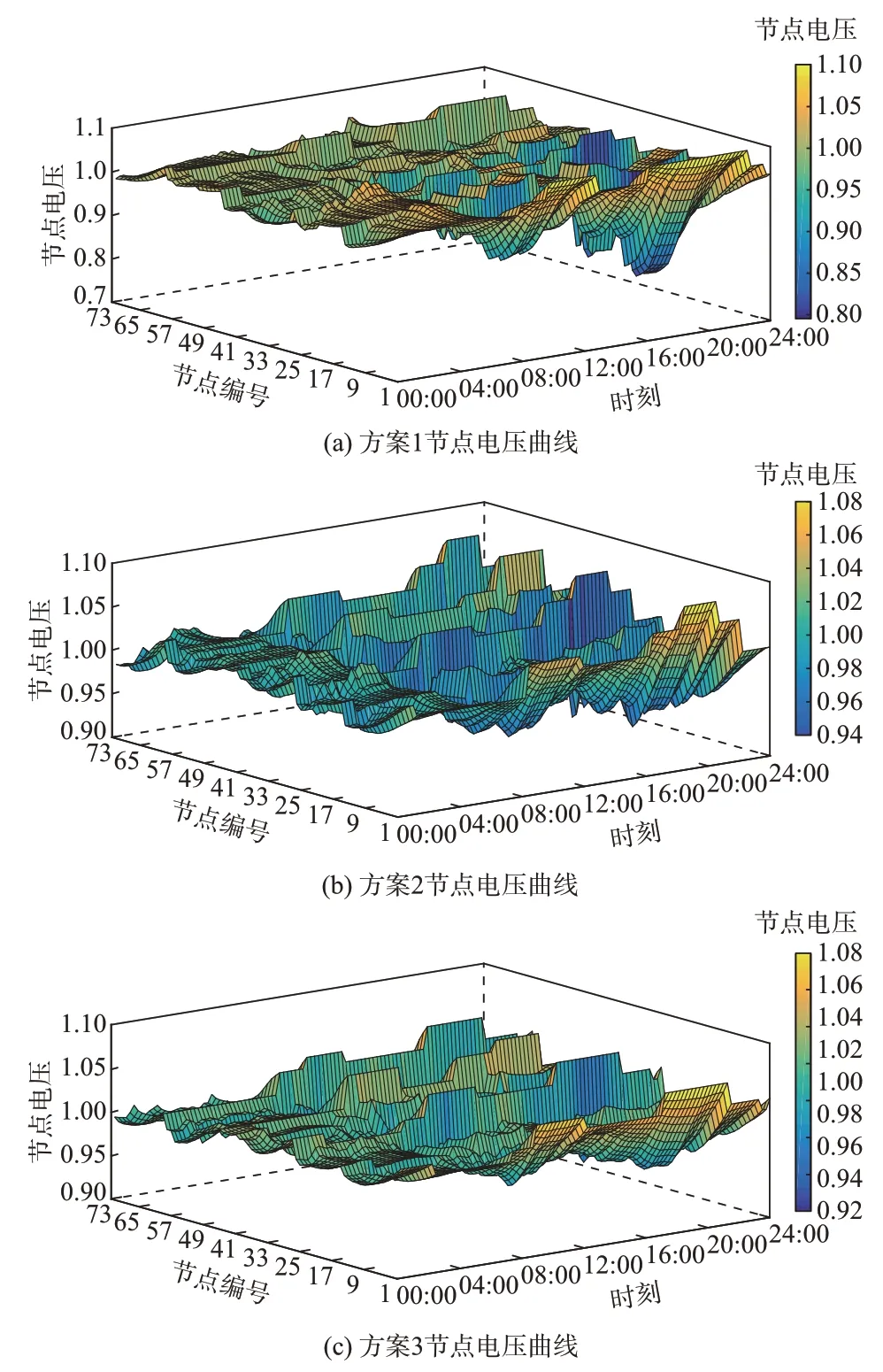
图3 3 种方案节点电压曲线Fig.3 Bus voltage curves of three schemes

在网损方面，方案1 的系统总网损最高，其中馈线A 和B 的网损量所占比例约为81%，主要是由于其馈线距离较长且负荷较重。系统通过柔性合环（方案2 和方案3）合理分配功率流动，使系统总网损分别下降了7%和8.1%，其中柔性互联装置的损耗分别为0.73 MW·h 和1.81 MW·h。由附录D 图D3和图D4 可知，方案3 的储能在网损较低时段吸收能量，并在网损较高时段（尤其是18：00—21：45）发出，大幅度降低了网损。

综上，自储能柔性互联配电网具有更好的全网电压调节和网损优化效果。

4.2.2 SESDC 控制策略分析

为验证本文提出的基于功率区间限制的储能控制策略及其参数选取的有效性。选择如下7 种案例进行对比分析。

案例1：设定储能区间宽度为0（等价于日前最优功率直接用于日内控制）。

案例2：设定储能区间宽度为5%PES，max。

案例3：设定储能区间宽度为10%PES，max（本文取值）。

案例4：设定储能区间宽度为15%PES，max。

案例5：设定储能区间宽度为20%PES，max。

案例6：设定日内优化储能充放电状态与日前相同（仅限制各时段储能充放电状态）。

案例7：不对日内优化做任何限制（等价于完全由日内优化决定储能出力）。

上述案例各时段储能功率变化情况如附录D图D3 所示，各场景的优化结果如表2 所示。

表2 各场景在不同区间宽度下的优化结果Table 2 Optimal results of various scenarios with different interval widths

由表2 可以看出，若不限制储能功率或者仅限制充放电状态难以取得良好的优化效果，储能区间宽度与日内最优目标值关系的讨论如附录E 所示，可以看出，随着储能区间宽度的增加，日内优化目标函数值呈现先减小后增大的趋势。

由表2 中实时优化前后的电压偏差数据可以看出，储能区间宽度在0～20%PES，max时，DG 功率突变造成的电压偏差和经过实时优化后的电压偏差，会随着区间宽度的增加而减小。案例6 与案例7 的电压优化效果较差，近似等于案例1，主要原因在于若不对日内优化中的储能输出功率加以限制，储能根据单时间断面最优进行充放电，造成电量放完或充满，导致实时优化无可调容量。综上所述，要保证日内优化效果，储能最优功率区间的取值应在0～10%PES，max；而区间范围在0～20%PES，max时，取值越大，实时电压控制效果越好，因此，本文将区间宽度设置为10%PES，max较为合理。

附录F 以场景1 在13：15 时DG 突变情况为例，对实时优化过程进行了分析，可以看出，实时优化方法能够依据电压实时反馈数据对SESDC 输出功率做出动态调整，具有良好的电压调节效果。此外，实时优化中的计算时长也是衡量性能的重要指标，因此，下面对PR-SOCP 算法性能进行进一步分析。

4.2.3 PR-SOCP 算法分析

本文利用二阶锥松弛将非凸、非线性模型转化为SOCP 模型，并应用多面体松弛技术将SOCP 模型线性化，算法有效性分析如附录G 所示。针对场景1，分别采用SOCP 与PR-SOCP 方法进行了对比，通过96 次仿真计算得出相应的算法性能对比如表3 所示。