电力系统参数空间暂态稳定边界构建及在线快速更新方法

田 园，汪可友，徐 晋，李国杰

（电力传输与功率变换控制教育部重点实验室（上海交通大学），上海市200240）

0 引言

在不断增长的经济压力和电力需求下，电力系统运行时的稳定裕度不断减小。系统调度人员经常需要在极度紧张的情况下，实时计算可用的传输能力或实时管理拥塞问题。其中，最具挑战性的环节之一就是如何在线快速评估系统暂态稳定性并采取进一步预防控制措施。传统暂态稳定评估方法中，时域仿真法［1］计算精度高、对模型没有限制，但耗时过长无法适应在线应用。而直接法［2］虽然提供了暂态稳定性的定量分析，但存在难以构建复杂系统能量函数以及保守性等问题。

近年来，机器学习方法［3-7］因其评估计算过程简单，不需要建立复杂的数学计算模型，在暂态稳定评估方面取得了显著成就。相关研究主要涉及深度置信网络（deep belief network，DBN）［3］、卷积神经网络（convolutional neural network，CNN）［4］、决策树（decision tree，DT）［5］、支持向量机（support vector machine，SVM）［6］和极限学习机（extreme learning machine，ELM）［7］等方法。基于机器学习的暂态稳定评估本质是学习电力系统的运行状态特征量与系统稳定与否等信息之间的映射关系。其中，文献［3］提出了一种基于DBN 的暂态稳定评估方法。该模型先使用无标注样本进行贪心无监督学习，后使用有标注样本进行监督学习以训练DBN 模型。能够在少量训练样本和含有无关特征的情况下获得较好的评估性能。文献［4］提出一种基于稳态特征量的CNN 综合评估模型。采用多个结构相同、参数不同的CNN 模型进行结果综合，得到“稳定”“不稳定”“不确定”3 种分类预测结果。并将结果不确定的样本送入时域仿真作进一步评估。上述方法主要关注对电力系统稳定与否进行分类，无法直接给出相应系统极限切除时间（critical clearing time，CCT）等暂态稳定性指标，距离实际应用仍有一定差距。

另一方面，电力系统运行方式多变，基于离线数据构建暂态稳定边界（transient stability boundary，TSB）时无法也不可能涵盖所有情况。因而，机器学习方法的预测准确度受限于其训练样本分布。而实际运行中，不断积累的电力系统数据能够为原有映射挖掘提供新的样本扩充。在线应用阶段中当系统出现新样本时，离线阶段所构建预测模型应当能够在无须重新大规模计算的基础上快速更新，以提高其适应性。

为此，本文提出了一种电力系统参数空间暂态稳定边界构建方法。对于给定的关键故障和故障前后网络拓扑结构，基于宽度学习系统（broad learning system，BLS）［8］构建极限切除时间与电力系统参数之间的映射关系，并结合阈值确定暂态稳定边界。通过构建二次比例因子对构建模型进行改进，以保证暂态稳定边界附近的最高预测准确率。为提高在线应用的适应性，提出了适应在线快速更新的增量策略，在无须重新训练整个网络的情况下进行模型快速更新。

本文采用IEEE 39 节点测试系统和中国南方电网实例系统对所提方法进行验证。通过对不同系统运行方式和故障情况进行分析，证明了本文所提模型相比其他方法具有更高的准确率和泛化性能。另一方面，快速更新策略在保证更大范围预测准确率的同时，大幅减少了模型训练时间，为在线暂态稳定评估与后续优化控制提供了支撑。

1 参数空间中的暂态稳定边界

暂态稳定评估主要目的是探究受到大扰动后，电力系统能否在一段时间内稳定到可接受的运行状态［9］。为提供一种可同时描述不同运行点暂态特性的方法，本文构建了一种系统参数空间中的暂态稳定边界，并为后续计及暂态稳定约束的最优潮流计算以及暂态稳定预防控制等问题提供暂态稳定约束。因而，该暂态稳定边界需具备以下特点：以故障前系统运行状态参数表示；最大程度减少实际系统故障切除时间阈值（稳定边界）附近的预测误差；所构建暂态稳定边界表达式必须是可微的。对于最优潮流和预防控制等应用，需要其可提供清晰的一阶和二阶偏导数。

为进一步说明参数空间中暂态稳定边界的含义，以3 节点系统为例（系统结构详见附录A 图A1），绘制其参数空间暂态稳定边界如图1 所示，其中P1和P2分别为发电机G1 和G2 的有功功率，均为标幺值。

图1 参数空间中的暂态稳定边界Fig.1 Transient stability boundary in parameter space

图1 为极限切除时间映射曲面CCT( p)（详见附录A 图A2，其中p=[ P1，P2]表示系统参数）在参数空间P1-P2中的等高线，即设置不同故障切除阈值tcl时暂态稳定边界在参数空间的投影。以设定故障切除时间阈值tcl=0.2 s 为例，暂态稳定边界CCT( p)-tcl=0 将潮流可行域［10］内空间分为了“稳定（极限切除时间大于0.2 s）”和“不稳定（极限切除时间小于0.2 s）”两部分。若在不考虑系统暂态稳定性的情况下调整系统运行状态，从运行点1变为运行点2，则预设故障发生后系统将失稳。因而，若能提前确定暂态稳定边界，调度人员即可对当前运行状态暂态稳定性进行快速评估，并在合理范围内调整系统运行状态。另一方面，实际应用中可根据所需情况选取不同tcl构成相应暂态稳定边界，以适应具体的需求。例如，采取相对保守的策略，增大故障切除时间阈值以消除漏判（将不稳定状态判断为稳定状态）的情况。

为此，若能够准确构建极限切除时间与电力系统参数之间的函数映射关系CCT( p)，则可结合预设阈值tcl得到相应暂态稳定边界以应用于在线暂态稳定评估和控制中。但需要注意的是，极限切除时间仅适用于包含故障切除的情况。为使稳定性指标适用于所有类型故障，可使用基于能量函数估算的暂态稳定裕度替代极限切除时间。

2 暂态稳定评估与控制框架

为说明拟构建暂态稳定边界的实际应用意义，本章提出了一种在线暂态稳定评估与控制框架，如图2 所示。

图2 暂态稳定评估与控制框架Fig.2 Framework of transient stability assessment and control

1）离线阶段

首先，基于时域仿真法获取关键故障下的初始训练样本。然后，基于BLS 构建极限切除时间与系统参数之间的映射关系。步骤如下：通过网络搜索法确定算法系统参数；基于误差修正（减少预设故障切除时间阈值附近的预测误差）构建相应故障下的CCT( p)；结合预设故障切除时间阈值tcl，确定暂态稳 定 边 界 CCT( p)-tcl=0。 其 中 ，p=[ p1，p2，…，pn]表示故障前系统运行状态参数向量（如发电机输入、负荷、线路传输功率和节点电压、相角等），n 表示特征参数个数。

2）在线阶段

基于离线阶段所构建的CCT( p)，结合预设故障切除时间阈值tcl，运行点p 暂态稳定裕度Δ CCT( p)可表示为：

当Δ CCT( p)＞0 时表示稳定裕度大于0，即此时在发生给定故障的情况下系统稳定；反之，系统不稳定。由于该方法首先构建极限切除时间与电力系统参数之间的函数映射关系CCT( p)，在实际应用中可根据所需情况，选取不同tcl构成相应暂态稳定边界，当预设阈值tcl发生变化时无须重复构建CCT( p)。另一方面，在线评估过程中，当未包含在原始样本集中的新运行状态出现时，将基于增量更新算法对已构建暂态稳定边界进行快速更新，以提高其对更大跨度的运行点变化的适应性。

同时，由于构建算法过程中采用指示函数的变体形式的非线性激活函数，因而所构建暂态稳定边界表达式高阶可微，其将用于暂态稳定预防控制模型中。以计及暂态稳定约束的极限传输功率（transient stability constrained total transfer capability，TSC-TTC）计算为例，如图2 所示，其过程循环以下步骤：关键故障筛选与排序→运行状态再分配→新运行状态暂态稳定评估，该研究将在后续工作展开。

3 暂态稳定边界构建与快速更新策略

3.1 基于宽度学习系统的暂态稳定边界构建

对于多机系统，针对某故障/故障后系统，潮流可行域内故障前系统运行点与暂态稳定性指标之间存在唯一的映射关系［11］。但计算中涉及大量耦合的非线性代数和微分方程，无法使用解析方法推导该映射函数。基于机器学习方法研究暂态问题的理论基础在于：包含物理机理的因果关系数据通常也表现出数据关联关系的外在特征［12］。但由于堆叠层和复杂网络架构，深度学习系统训练所得模型的堆叠特性往往非常复杂，难以直接应用于后续优化控制模型中［13-14］。而BLS［8］从横向上进行神经元扩展，不在深度上进行堆叠，在提高模型训练速度的同时提供了更为清晰的映射表达式，在后续应用中更具优势。

BLS 架构如图3 所示。

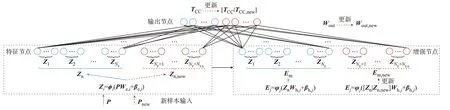
图3 BLS 架构Fig.3 Framework of BLS

如图3 所示，BLS 原始输入通过转换表征为特征节点Z，并且通过增强节点E 从宽度上进行扩展。时域仿真法由于其可靠性和对模型没有限制的特性，用于离线阶段获取初始训练样本。某关键故障下初始数据样本集{ P，TCC}表示为：

式中：P 为运行点参数矩阵；TCC为对应系统极限切除时间向量；N 为总样本个数，每个样本表示该故障情况下系统的一种运行状态；行向量p1，p2，…，pN为空间Rn中的向量；tcc，N为对应第N 个样本的极限切除时间。

基于训练样本数据{ P，TCC}∈RN×(n+1)和NF个特征映射函数φi(⋅)，第i 个特征节点Zi表示为：

式中：We，i和βe，i为［-1，1］内随机生成的算法参数。为克服其随机性，本文使用稀疏自动编码［8］将随机特征调整为一组稀疏、紧凑的特征。

令特征节点集合Zn≜[ Z1，Z2，…，ZNF]，则第j 个增强节点Ej表示为：

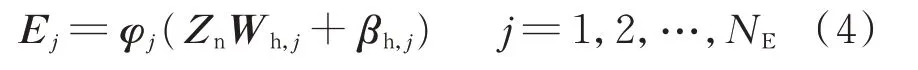
式中：Wh，j和βh，j为在［-1，1］内随机生成的算法参数；φj(⋅)为激活函数；NE为增强节点个数。

设增强节点集合为Em≜[ E1，E2，…，ENE]，则输入（运行点参数矩阵P）和输出（对应系统极限切除时间向量TCC）之间的映射表示为：

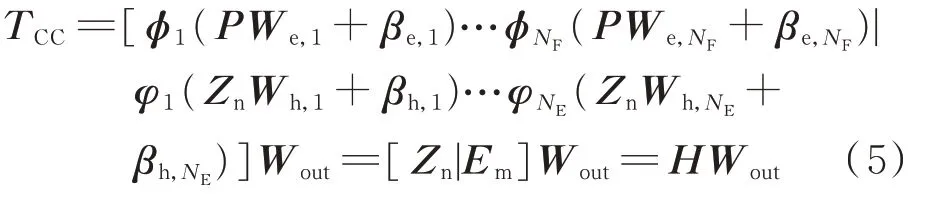
式中：函数φi(⋅)和φj(⋅)的选取没有特殊限制，可根据实际问题进行筛选［8］。

本文中，使用如下映射函数进行模型构建：

1）线性函数：φ(w，b，x)=wx+b。

2）高斯函数：φ(w，γ，x)=exp(-γ‖x-w‖2)。

3）指数函数：φ(w，b，x)=exp(-(wx+b))。

4）Sigmoid 函数：φ(w，b，x)=1/(1+exp(-(w⋅x+b)))。

上述函数中：w，b，γ 为模型系数；x 为输入样本。

进而，由于所使用非线性激活函数均采用指数函数的变体形式，因此所构建的CCT( p)高阶可微，存在一阶和二阶偏导数。同时，由式（5）可知，构建参数空间中极限切除时间映射函数即为确定输出权重矩阵Wout。给定惩罚因子λ 时，Wout由下述优化问题求得：

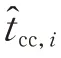
综上，极限切除时间与运行点p 的映射关系为：

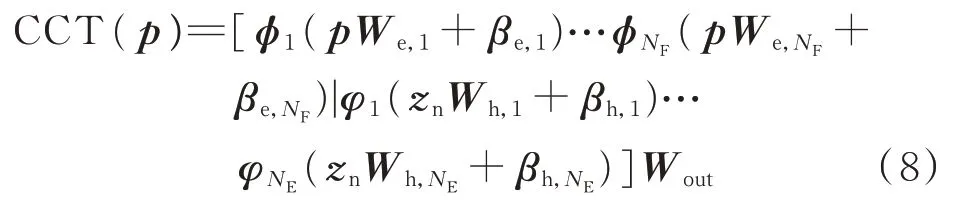
基于式（8），结合预设故障切除时间阈值tcl即可获得当前故障情况下的参数空间暂态稳定边界。

3.2 在线快速更新策略

为充分利用实际系统运行中新出现的样本，本节提出一种暂态稳定边界快速更新策略。基于计及增量学习的BLS（incremental strategy based BLS，IS-BLS）［8］，当新样本{ Pnew，TCC，new}加入时，首先增加NFA个特征节点：

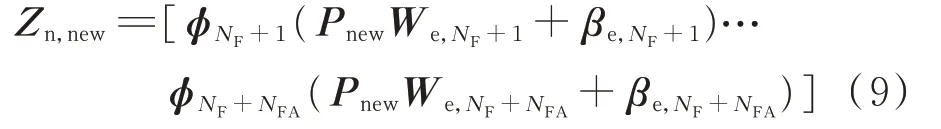
如图3 所示，基于新增加的特征节点Zn，new，新增NEA个增强节点，合并表示为：

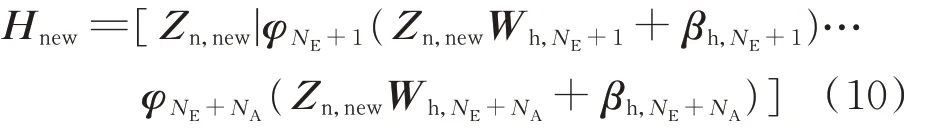
基于岭回归对输出矩阵进行更新，表示为：

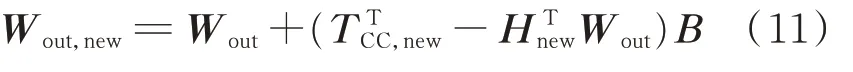
其中：

由式（12）可知，当有新样本{ Pnew，TCC，new}加入时，输出矩阵Wout，new的更新过程仅需计算对应矩阵的伪逆，无须重新训练整个网络。因此，基于ISBLS 的增量学习策略，可在保证预测准确率的同时对暂态稳定边界进行快速更新，提高了所构建暂态稳定边界在线应用的适应性。综上，暂态稳定边界构建及快速更新策略算法伪代码详见附录B。

4 算例分析

4.1 参数空间中暂态稳定边界分析

首先，采用IEEE 39 节点系统［9］进行分析（系统图详见附录C 图C1）。该系统共包含10 台发电机、39 条母线和46 条线路，代表美国新英格兰州1 个345 kV 的电力网络，其中1 号母线上的发电机是平衡机。根据系统潮流分布可将整个系统分为3 个区域。为绘制2 维参数空间示意图，改变节点3 和4 的发电机组出力：PGi=PGi，0[1+(k-2)×0.05]，其中PGi，0为发电机i 初始有功出力值，k=1，2，…，20。发电机采用二阶经典模型，负荷模型采用恒阻抗模型。令关键故障分别发生在靠近母线4 和16 处（记为故障1 和故障2），故障类型为最严重的三相短路故障。分别考虑不同切除策略，故障1 切除后不切除线路，系统拓扑不变；故障2 切除母线15 和16 之间线路。选取发电机节点3 和4 的机组出力作为系统参数p=[ PG3，PG4]，每种故障情况包含400 个样本。选取70%样本作为算法网络训练集，剩余30%作为测试集。基于网络搜索法确定模型的最优参数(NF，NE)，搜索参数空间维度为[1，300]×[1，300]。φ(⋅)和φ(⋅)分别选取线性、指数函数。由于篇幅限制，正文中仅列出效果最优的映射函数，其他映射函数组合构建结果对比详见附录C 表C1。使用以下指标验证模型效果。

1）均方根误差（root mean squared error，RMSE）：

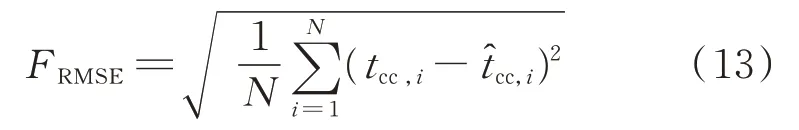
RMSE 主要反映模型构建精度，提供实际值与预测值之间的绝对差距。

2）相对误差平均值（relative error mean value，REMV）：

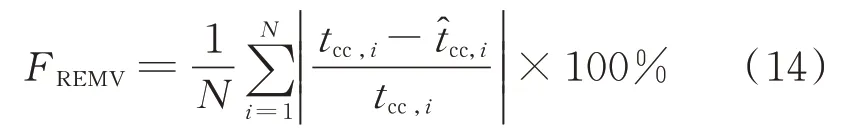
REMV 主要用于测量模型预测的质量，反映预测值与真实值之间的相对误差。

计及和不计及临界误差修正时算法预测结果对比如表1 所示，其中TSB1 和TSB2 分别表示故障1和故障2 情况下所构建暂态稳定边界。其中，故障切除时间阈值tcl设为0.2 s［15］；临界误差表示在tcl±0.01 s 范围内的样本误差；最大测试误差为所有测试样本中误差的最大值。特别地，时间阈值tcl对CCT( p)构建并无影响，实际使用时需根据实际系统情况灵活调整。

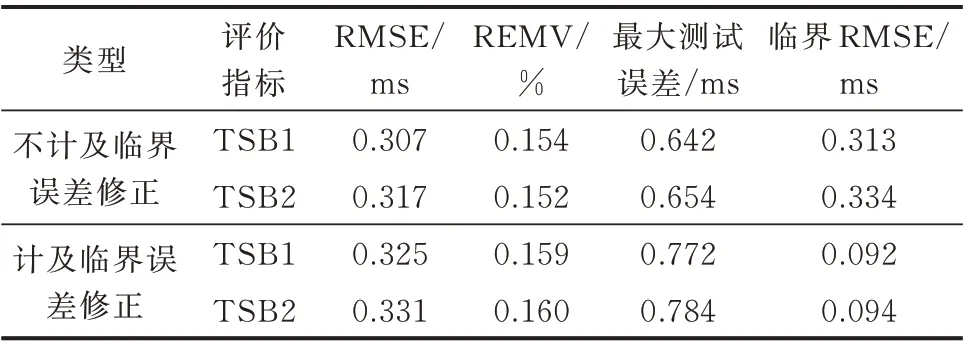
表1 不同故障情况下暂态稳定边界构建结果Table 1 Construction results of transient stability boundaries with different faults

从表1 中可以看出，计及临界误差修正后样本的临界误差RMSE 均小于0.1 ms，提高了暂态稳定边界附近的预测精度。虽然降低临界误差的同时，总预测误差RMSE 比不计及临界误差修正时稍有增大，但总预测误差仍在0.4 ms 内，不同故障情况下最大测试误差也均小于0.8 ms，在可接受范围内，说明了临界误差修正的合理性。计及临界误差修正后所构建的2 种故障情况下的CCT( p)曲面如图4所示。

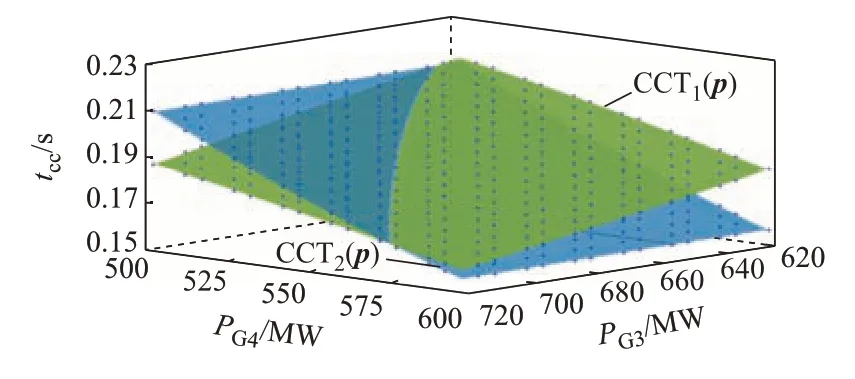
图4 2 种故障下极限切除时间映射关系Fig.4 Mapping relationship of critical clearing time with two faults

图5 为所构建极限切除时间映射曲面（图4 中蓝色和绿色曲面）在参数空间PG3-PG4中的投影。如图5 所示的2 维参数空间中，TSB1 与TSB2 分别表示故障1 和故障2 的暂态稳定边界。基于TSB1 和TSB2，参数空间被划分为“故障1 和2 稳定”“故障1和2 不稳定”“仅故障1 稳定”和“仅故障2 稳定”4 个部分。进而，对于给定的当前系统运行状态可快速对其暂态稳定性进行分析。

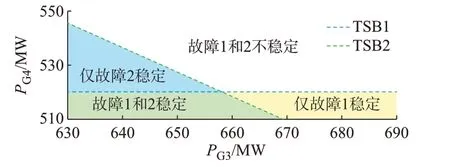
图5 电力系统参数空间中的暂态稳定边界Fig.5 Transient stability boundaries in parameter space of power system

为进一步分析不同输入特征（PG3和PG4）对预期目标响应（极限切除时间）的边际影响，附录C 图C2中绘制了不同输入特征对应的部分依赖图和个体条件期望图。如图C2 所示，不同故障下PG3和PG4对预期目标响应极限切除时间影响程度不同。对比图C2（a）中2 幅图可知，故障1（靠近母线4 处发生三相短路）发生时，极限切除时间对发电机G4 的出力变化更为敏感。PG3对模型输出几乎没有影响；发电机G4 的出力PG4与模型输出之间呈现单调递减关系，即PG4增加，极限切除时间降低，系统暂态稳定性降低；而当故障发生在靠近母线16 时，发电机G3 和G4 的出力与模型输出之间均呈现单调递减关系，其变化都将在较大程度上影响系统暂态稳定性。基于此，电网调度人员可进一步了解不同系统参数对暂态稳定性的影响，进而为其在暂态稳定极限内调整传输功率提供依据。

此时，所构建CCT( p)的紧凑形式表示为：

式中：a、bi、c、di和ei为训练所得模型系数。结合预设断路器故障切除时间阈值tcl，其对应暂态稳定边界表示为CCT( p) -tcl= 0。

4.2 不同负荷运行方式下的算法性能分析

考虑更大范围运行点变化，改变IEEE 39 节点系统区域3 中各负荷节点有功功率：PLi=PLi，0[1+(k-2)×0.3]，其中PLi，0为负荷节点i 初始有功值，i=16，20，21，23，24，k=1，2，…，5。相应改变区域1和3 发电机出力保证系统功率平衡。故障点与故障类型同4.1 节，每种故障情况包含1 024 个样本。为测试不同算法的泛化性能，按照样本空间分布分别选取总样本前10%、30%至70%样本作为训练集，末尾30%作为测试集。首先，对比如下2 种运行点参数选取策略：

策略1：选取除平衡节点外区域1 和3 中发电机出力作为系统参数。

策略2：选取除平衡节点外发电机出力与各变化负荷节点有功功率作为系统参数。

2 种运行点参数选取策略对比结果如附录D 图D1 所示。观察图D1，对比策略1 和2 结果可知，当选取总样本前10%样本作为训练集时，由于训练样本在参数空间的分布与测试样本在参数空间的分布差异较大，其测试误差均较其训练误差有较大差异，泛化误差大。但随着训练样本量的增加，当使用前30%样本训练模型时，测试误差与训练误差基本相同。后续增加训练样本，模型预测准确率变化不大。当系统参数空间维数超过2 维时，高维空间中暂态稳定边界无法直观画出，需要通过降维方法投影至三维空间以进行可视化。由于篇幅限制，降维至三维空间的暂态稳定边界及部分依赖图详见附录D 图D2 和图D3。

另一方面，当训练样本较少时（仅以总样本前10%～20%进行模型训练），策略2 的训练结果略差于策略1。这是由于当样本量过少时，样本包含参数越多越容易产生过拟合问题。但随着样本的增加，策略2 的预测准确率迅速提高。如表2 所示，当使用30%样本进行训练时，策略2 预测结果与使用70%样本训练结果基本一致，误差均在0.4 ms 以内，说明算法具有良好的泛化性能。

由于BLS 的本质是一种随机向量函数链接单隐层神经网络，因而选用SVM 和ELM 模型［16］进行对比。以策略2 构建系统参数集合，其中，SVM 模型采用高斯函数作为核函数，ELM 模型采用Sigmoid 函数作为激活函数。由于篇幅限制，正文中仅列出了效果最优的映射函数，更多映射函数构建结果参见附录D 表D1 和表D2。2 种算法均采用网格法和交叉验证进行参数寻优［14］。模型预测结果如表3 所示。

表2 不同系统参数选取策略结果对比Table 2 Results of different strategies for system parameter selection

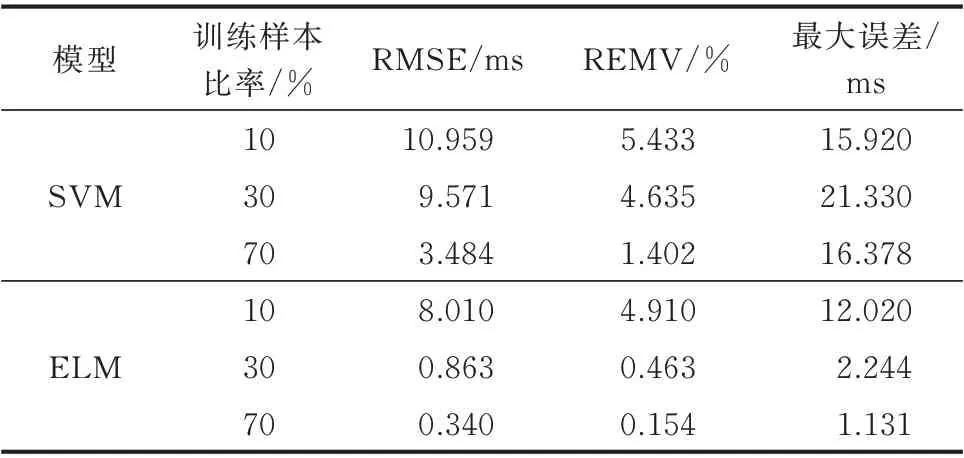
表3 SVM 和ELM 模型预测结果Table 3 Prediction results of SVM and ELM models

对比表2 中策略2 的结果，BLS 模型预测结果优于SVM 和ELM 模型。可以观察到，当训练样本达到总样本量的30%时BLS 模型和ELM 模型预测结果较10%时均有较大提高，但BLS 模型预测误差仅为ELM 模型的1/2。说明当训练样本有限时，BLS 模型具有更好的泛化性能，应用于在线暂态稳定评估过程中更具优势。

4.3 快速更新策略适应性分析

为验证暂态稳定边界快速更新策略的效率及其预测准确率，本节选取4.2 节总样本中前70%样本作为训练集备选，剩余30%作为测试集。首先，以总训练样本的前20%进行训练，然后在最初20%训练样本基础上，每次增加20%样本对已构建暂态稳定边界进行更新，直到所有样本都被训练为止，结果如表4 所示。同时，使用计及增量策略的在线序列ELM（online sequential ELM，OS-ELM）模型［15］进行对比，结果如表5 所示。

表4 更新策略结果Table 4 Result of update strategy

表5 OS-ELM 模型预测结果Table 5 Prediction result of OS-ELM model

表4 对比了使用和不使用更新策略时暂态稳定边界的构建结果。观察训练样本比率为40%～60%和60%～100%时的IS-BLS 模型预测结果，使用更新策略的IS-BLS 模型预测准确率与直接使用对应数量样本重新训练整个模型时基本一致，但训练时间仅为其1/3，说明了IS-BLS 模型在无须重新大规模计算的基础上实现了准确预测。另一方面，使用训练集前60% 样本进行训练时，2 种模型的RMSE 已小于0.4 ms，最大误差小于1 ms，说明BLS 模型在训练样本较少的情况下，仍能达到可接受的准确率。

对比表4 和表5 结果可见，当可用于训练暂态稳定边界的样本较多时（40%～60% 和60%～100%），OS-ELM 训练结果与IS-BLM 结果相差不大，IS-BLM 略优。但当训练样本较少时，IS-BLM预测准确率高于OS-ELM，泛化性能更好。同时，由于模型结构具有一定相似性，IS-BLM 和OSELM 训练时间相差不大，均比未使用增量策略减少了2/3 左右。

4.4 实际系统应用分析

为进一步验证所提方法在实际电力系统中的适用性，本文使用中国南方地区电网系统进行实例分析，其主网架结构如附录E 图E1 所示。

基于PSD-BPA 软件，在初始潮流方式基础上，在80%～120%（以1%为变化步长）基准负荷下，改变区域XY 中负荷有功功率和无功功率（对应调整发电机出力保证潮流收敛），共得到1 600 个潮流方式。考虑N -1 关键故障：在区域XY 和N6 联络线靠近送端母线处发生三相短路故障。选取故障前区域XY 中各发电机出力与各负荷节点有功功率作为系统参数。从总样本中选取前70%样本作为训练集，剩余30%作为测试集。首先，以训练集样本的前50%构建基础暂态稳定边界，然后每次添加训练集剩余样本的25%作为新增输入样本，直到将所有1 120 个训练样本输入模型为止。同时，采用OSELM 模型［17］进行对比。试验结果如表6 所示。

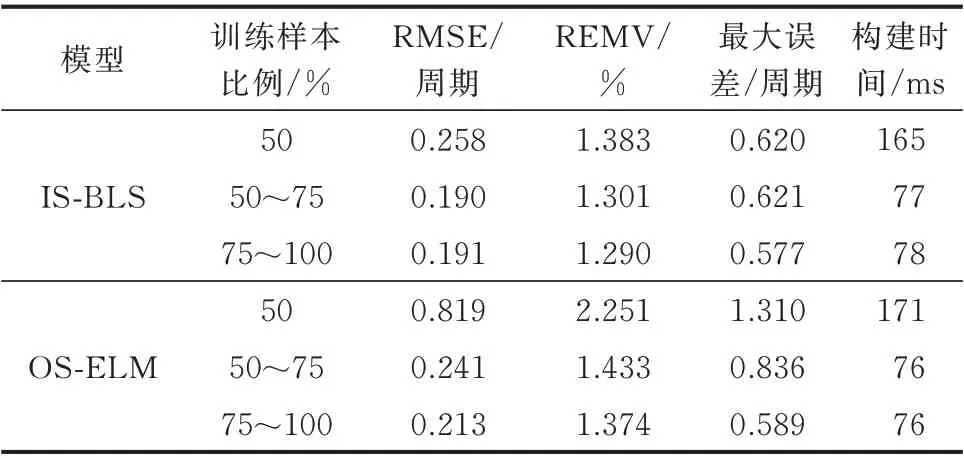
表6 IS-BLS 和OS-ELM 模型结果对比Table 6 Result comparison between IS-BLS and OS-ELM models

对比OS-ELM 模型所得结果，当训练样本较少时基于IS-BLS 的暂态稳定边界构建方法表现出了更优越的预测和泛化性能。同时，与4.3 节结论一致，基于IS-BLS 的更新策略保证了实时更新模型的快速性和有效性。

需要注意的是，本文所构建暂态稳定边界针对给定的关键故障和既定故障前后的网络拓扑结构。当系统故障类型和故障位置发生变化时需要重新构建。为适应在线应用，实际中对所有可能故障情况和故障位置进行离线构建是不现实的。因而，需要先对系统关键故障进行筛选以获取关键故障集合，进而考虑对系统影响最严重的故障类型进行暂态稳定边界构建。另一方面，由于电力系统拓扑在不同故障情况下变化不大、电气耦合关系不变，满足基于特征选择的迁移学习算法特征。因而，可以利用迁移学习方法在样本较少的情况下快速构建其他故障暂态稳定边界。该部分内容将与关键故障集合的快速筛选方法一起作为后续研究内容。

5 结语

本文提出了一种电力系统参数空间暂态稳定边界构建和在线快速更新方法。通过横向扩展的BLS 算法构建了故障前系统运行状态参数和极限切除时间之间的映射关系，并结合稳定阈值给出了相应暂态稳定边界。为保证暂态稳定边界附近的预测可靠性，构建了二次比例因子对临界误差进行了修正。通过对算例进行分析，计及临界误差修正后，模型大幅度减小了稳定边界附近的预测误差，提高了暂态稳定评估的可靠性。与其他方法相比，该模型具有更高的预测准确率和泛化性能。同时，计及更新策略的IS-BLS 模型能够在提高更新速度的同时保证预测准确率，为模型在线快速更新提供了可能。

另一方面，BLS 模型提供了清晰的暂态稳定边界表达式，可快速分析不同运行点暂态稳定裕度，在实际应用中更具优势。此外，所构建暂态稳定边界高阶可微，将作为暂态稳定约束用于后续暂态稳定预防控制研究中。此内容将作为研究的下一阶段目标。

本文中实验方案制定是在瑞典皇家理工学院Marina Oluic 博士和Mehrdad Ghandhari教授大力支持下完成，在此向他(她)们表示衷心的感谢。同时感谢博士后创新人才支持计划项目(BX20200221)的支持。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。