基于波前陡度的输电线路单端行波故障测距

2021-05-07朱柏寒马金杰

电力系统自动化 2021年9期

朱柏寒，陈羽，马金杰

（山东理工大学电气与电子工程学院，山东省淄博市255000）

0 引言

输电线路准确的故障定位，有利于工作人员快速进行故障处理，从而减少停电时间、降低故障损失。现有的故障测距方法主要分为行波法和阻抗法，而行波法主要分单端法、双端法和多端法［1-2］。单端法利用故障初始行波和故障点反射波到测量点的时间差测距；双端法通过检测故障行波到达线路两端波头的时间进行测距，实际输电线路行波故障测距系统一般以双端法为主，单端法为辅［3-4］。当线路某一端行波装置未能捕捉到故障初始行波时，双端法就会失败，为避免该问题有文献研究了多端法。多端法利用故障初始行波透射到母线上其他线路时多点记录的行波信号进行测距［5］。但对于一些末端线路，无法应用多端测距方法。对于末端线路，单端法如能自动准确测距，将有效提高测距系统的可靠性。

单端法受相邻线路和阻抗不匹配点折反射的影响，故障点反射波头识别困难［6-11］。为解决该问题，文献［7-9］提出了工频测距和行波故障测距相结合的方法，先对单端采集的故障行波进行波头识别，得到几个可能的故障点反射波头对应的距离，再通过阻抗法计算故障距离，并对行波法得出的故障点反射波头进行筛选，最接近的故障距离作为测距结果，该方法需同时采集工频信号和行波信号，实现时一般通过故障录波器与行波故障测距装置相配合。文献［10］推导出二次侧行波波头衰减振荡的数学表达式，并通过数值计算的方法给出衰减振荡频率与二次侧传输电缆长度的关系。行波线模和零模的关系也可以识别故障点反射波波头，文献［11］通过第2个到达的反向行波中零模与线模的极性来识别故障点反射波。文献［12］利用神经网络训练学习方法，估算出零模波速度，根据零模与线模波速差得出一个初步故障距离，该方法近端故障时容易受到干扰。

故障行波在线路上传播会发生畸变，故障行波波头的畸变程度与故障距离相关，行波波形畸变主要由色散引起，不同频率的行波分量衰减速度与传播速度不同，高频分量传播速度快，衰减速度也快，随着传播距离增大其波形畸变也越严重，其中零模分量特征较为明显［13-14］。文献［15］考虑了输电线路的频变特性和行波的色散效应，计算了0～1 MHz 频带内不同模量通道的传播系数。文献［16］定义了波头突变幅值与最高频率分量和最低频率分量到达时间差的比值为波头平均斜率，用其表征波头畸变。文献［17］提出了一种利用波前信息的直流输电线路行波保护原理，该方法基于故障零模电流行波波形畸变程度与故障距离相关原理，利用波形相关系数，实现了输电线路区内外故障判别。文献［18-19］在文献［15］的基础上，利用矢量拟合法对传播系数拟合，根据拟合结果，选取广义Logistic 函数对行波波前拟合，用函数的陡度来表示波前畸变程度，考虑到平波电抗器对波前畸变的影响，对陡度进行整定，实现了区内外故障的判别。

基于故障初始行波的波前陡度与故障距离相关的特性，本文分析了影响波前畸变的因素，提出了波前陡度与小波波头识别相结合的单端自动测距方法，并通过算例验证了方法的有效性。

1 行波畸变

1.1 故障行波在输电线路上的色散

输电线路发生故障时，将产生向线路两端传播的故障初始行波。故障初始行波可以视为一个全频带阶跃波。不同频率的故障分量衰减速度与传播速度不同，导致行波畸变，这种现象称为行波的色散。根据传播通道不同，分为线模分量和零模分量，可以通过凯伦贝尔变换获得。线模通道由线路导线构成，零模通道由线路导线与大地构成。行波在输电线路上的传播特性用传播系数γ 表示，表达式如下：

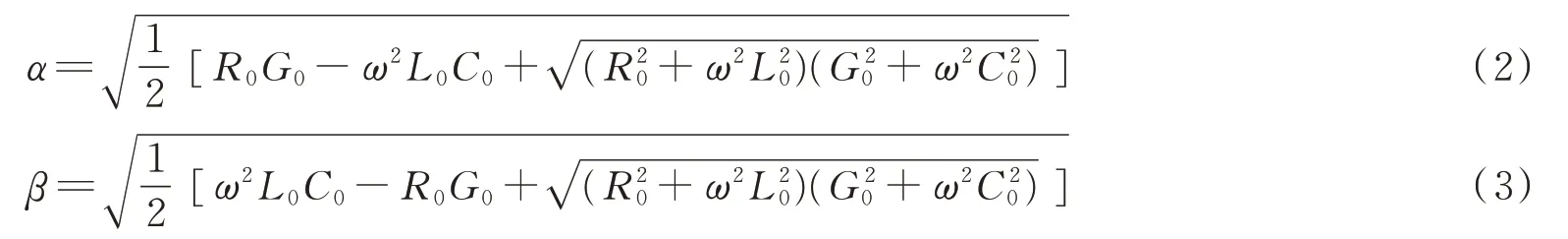
式中：α 为表示行波沿线衰减特性的衰减常数；β 为表示行波沿线相位变化特性的相位常数；ω 和R0、G0、L0、C0分别为角频率和单位线路长度电阻、电导、电感、电容。

波速度、频率、相位常数的关系如式（4）所示，不同频率分量所对应的不同波速度是导致行波畸变的主要因素。

图1 不同故障距离下的初始零模电流行波波头Fig.1 Traveling wave heads of initial zero-mode current at different fault distances

由于线模和零模通道的参数不同，对应的分量色散程度也不同，零模分量受大地频变特性与大地电阻率的影响，色散现象较为明显［13-15］。

1.2 行波畸变影响因素分析

线路发生故障后，测量端采集到的故障初始行波零模分量的畸变程度与故障距离相关，研究并利用两者之间的关系，可弥补基于小波变换的单端行波故障测距方法中故障点反射波识别困难的不足。

故障行波零模分量的畸变受多种因素影响，其中故障初相角、过渡电阻主要影响行波幅值，对行波畸变影响较小；故障距离、大地电阻率对行波畸变影响较大［6，13-15］。由于不同故障情况下，故障初始行波幅值不同，为统一比较，下文的波形曲线为归一化处理后的结果。

1.2.1 故障距离对行波畸变的影响

以220 kV 架空输电线路为例，如附录A 图A1所示。使用PSCAD 建立了相应仿真模型，在M 端采集的不同故障距离的初始行波如图1 所示。由图1 可知，随着故障距离的增大，故障初始行波的波前畸变越明显。

1.2.2 大地电阻率对行波畸变的影响

故障行波零模分量受大地电阻率ρ 影响较大。输电线路跨域广泛、土壤性质多样且分布不均匀，例如：黏土、砂质黏土、黄土和沙土等电阻率各不相同。

2 波前畸变与故障距离

行波畸变主要与故障距离和大地电阻率相关。行波波前部分可使用广义Logistic 函数进行拟合［18］，函数表达式为：

式中：L、k、b 为待求参数。函数中的k 为函数的陡度，可用k 表征波前的畸变程度，为方便理解以下称k 为波前陡度。不同大地电阻率情况下，故障距离与故障初始行波波前陡度k 的关系如图2 所示。

图2 不同大地电阻率情况下波前陡度与故障距离的关系Fig.2 Relationship between wavefront steepness and fault distance with different earth resistivities

3 基于波前陡度的单端行波故障测距原理

线路发生故障后，对记录的单端波形求取故障行波的小波模极大值，可以确认故障初始行波及各反射波的到达时间，但无法识别出故障点反射波，需要其他方法来辅助识别。根据故障初始行波波前陡度与故障距离的关系可求出一个初步故障距离，该距离由于受具体线路大地电阻率和计算误差影响，其测距精度不足，但可以给出大致距离，协助进行故障点反射波波头的识别，从而实现自动准确测距。

3.1 单端行波故障测距原理

单端行波故障测距利用线路故障时在测量端采集到的第1 个行波浪涌与第2 个行波浪涌之间的时间差计算测量端与故障点之间的距离。由于线模分量较为稳定，测距中一般采用线模分量。计算公式如式（6）所示。

式中：A 为测量端；F 为故障点；dAF为故障点到测量端的距离；ΔT 为时间差。

3.2 波前陡度与故障距离的关系

波前陡度与故障距离的关系式难以直接获取，既然它们之间具有图2 这样的对应关系，可以通过数据拟合得出表达式。本文选取含不同衰减速度分量的ExpDec2 函数进行拟合。ExpDec2 函数为：

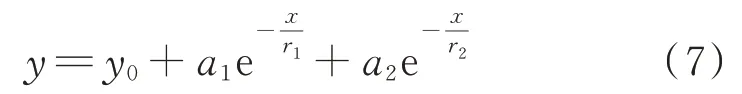
式中：y0、a1、a2、r1、r2为常数，其中a1和a2为比例系数，r1和r2为衰减常数；x、y 分别为自变量和因变量。考虑到大地电阻率对波前陡度的影响，得出含大地电阻率的波前陡度与故障距离的关系表达式如下。

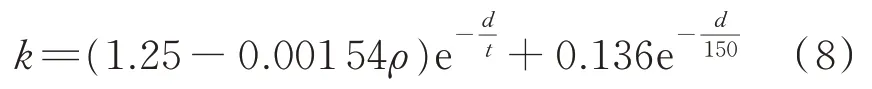
式中：d 为初步故障距离；大地电阻率ρ ∈(100，500)，当ρ ≥500 时，取ρ=500；t=22-0.028ρ，t ≥16.4。

3.3 故障点反射波头识别

3.3.1 获得多个测距结果

故障点反射波头的识别是单端测距的关键环节，当发生故障后，对采集到的故障波形进行凯伦贝尔变换，获得其线模分量与零模分量。求取线模分量小波模极大值，可得故障初始行波和其他反射波到达测量端的时间［20］。由于无法确认故障点反射波头，使用单端测距式（6）将得到多个测距结果，需要对其进行筛选。

小波变换由如下所示的Mallat 算法式（9）实现，详细参数参考文献［21］。其中j ∈[1，∞]；S2jf (n)为小波变换结果的逼近分量；W2jf (n)为变换结果的小波分量。

3.3.2 测距结果筛选

首先对故障初始行波零模波前采样点进行归一化处理，设置一般线性约束条件k＞0、L＞0，为保证拟合精确度，使用Levenberg-Marquardt 算法［22］对归一化后的波前数据进行拟合，拟合函数如式（5）所示。对故障初始行波的零模分量波前拟合可得波前陡度k，将k 代入式（8）可求得一个初步故障距离。

使用初步故障距离对测距结果进行筛选，确认故障点反射波头及其对应的测距结果，从而得到准确的故障距离。

3.4 大地电阻率的获取

大地电阻率对波前陡度存在一定的影响，为了减少其产生的误差，式（8）考虑了大地电阻率。但实际应用中，大地电阻率难以直接获取，可利用实际的故障数据对其进行修正，通过将实际故障距离与波前陡度代入式（8）估算出大地电阻率。

4 算法步骤

步骤1：线路发生故障后，对记录的波形进行凯伦贝尔变换，求取线模分量小波模极大值，获得故障初始行波波头及各反射波头到达测量端的时间；通过单端行波故障测距式（6）得出n 个测量结果di，其中i=1，2，…，n。

步骤2：拟合故障初始行波零模分量波前部分，提取其陡度k。

步骤3：ρ 的初始值为100 Ω ⋅m，将k 代入式（8）计算得出初步故障距离d。

步骤4：用初步故障距离d 对测距结果di进行筛选，最接近d 的结果即为最终测距结果。

步骤5：根据实际故障距离和波前陡度k，决定是否需要对大地电阻率ρ 进行修正，若需要修正则将修正后的ρ 值替换步骤3 中的ρ 值。

5 仿真验证

本文以图3 所示220 kV 架空输电线路为例，在节点A 处安装了行波故障测距装置。使用PSCAD建立仿真模型，在F 点处设置故障。故障发生后，在A 点采集故障行波，采样频率设置为1 MHz。

图3 仿真模型Fig 3 Simulation model

5.1 不同故障距离的测距

以发生在AC 线路上的单相接地故障为例，分别设置故障距离为60 km 和90 km，行波到达时间如附录A 表A1、表A2 所示。以60 km 为例，无法判断波头2、3 哪一个为故障点反射波，使用单端测距公式得出60.0 km、90.1 km 两个测距结果，通过波前陡度求得初步故障距离为59.0 km，所以波头2 为故障点反射波，最终测距结果为60.0 km。

5.2 不同故障情况下的测距

大地电阻率为100 Ω ⋅m 情况下，不同故障类型、过渡电阻和故障初相角的测距结果分别如附录A表A3 至表A5 所示。

5.3 大地电阻率未知情况下的测距

现场应用时，大地电阻率一般是未知的，这样会使测距误差增大，在极端情况下还会导致测距失败。例如，实际大地电阻率为300 Ω ⋅m，以100 Ω ⋅m为计算值，测距结果如表1 所示。因此，需要根据实际故障数据对大地电阻率进行修正，将测得的波前陡度及实际的故障距离代入式（8）计算得大地电阻率为280 Ω ⋅m，并使用修正后的值进行测距，测距结果如表1 所示。