电力系统强迫振荡源的时频域定位方法

姜 涛，李孟豪，李 雪，李国庆，陈厚合

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林省吉林市132012）

0 引言

随着电网结构增强、各类阻尼控制装置大规模配置，传统电力系统弱阻尼低频振荡已得到较好的抑制，强迫振荡成为威胁电力系统安全稳定运行的主要因素之一［1-2］。2011 年2 月26 日中国贵州发耳电厂因高压调门伺服卡功能故障导致强迫振荡，在现场人员强制关闭高压调门后振荡平息；2013 年5月8 日中国南方电网某电厂在阀切换过程引发强迫振荡，造成发电机解列，带来了巨大的经济损失［3-4］。强迫振荡通常是由持续周期性的小扰动诱发，当扰动频率接近系统固有振荡频率时，将导致全网发生振荡［5-7］。由于强迫振荡具有随机性强、起振快、扰动消失后振荡迅速衰减等特点，因此，快速、准确定位强迫振荡源是抑制电网强迫振荡的首要工作［8-9］。

目前，常用于强迫振荡源定位的主要方法是振荡能量函数法［10-12］。文献［10］提出了能量函数法的基本概念，并推导出系统各元件的能量函数构建模型；在此基础上，文献［11-12］依据系统强迫振荡过程中元件的能量转换特性定位振荡源，从能量的角度阐述了强迫振荡与自由振荡的区别。上述方法虽可有效辨识出系统振荡源，但其定位结果依赖于系统详细的数学模型和准确的模型参数［12］。随着电网互联规模不断扩大，在实际系统中获取详细的系统元件模型和准确的系统运行参数十分困难［13］。近年来，随着以同步相量测量单元（synchrophasor measurement unit，PMU）为基础的广域测量系统（wide area measurement system，WAMS）日渐完善，利用广域量测信息来分析和研究电力系统强迫振荡已成为可能，使得基于广域量测信息的系统强迫振荡源定位方法得到了快速发展［14-15］。由于该方法无须构建系统元件详细的能量函数，能够实现振荡源的在线定位，因而受到科研人员的广泛关注［15-17］。文献［16］提出了耗散能量流（dissipation energy flow，DEF）的概念并证明其与阻尼系数的一致性，实现了基于广域量测信息的强迫振荡源定位；文献［17］进一步利用正常运行状态下的电网量测数据分析支路耗散能量，提出借助瞬态耗散能量实现强迫振荡源的在线定位；文献［18-19］将DEF 分别应用于次同步强迫振荡与超低频振荡中，并验证了其有效性。

上述方法虽实现了基于广域量测信息的强迫振荡源定位，但均需从电力系统的广域量测信息中分离出所含强迫振荡模式的时域分量，然后根据所分离的强迫振荡模式分量来计算相应的DEF，计算过程较为繁杂。为此，文献［17］采用带通滤波（bandpass filter，BF）实现了强迫振荡模式分量的有效提取，进而定位了强迫振荡源。该方法易于实现、计算简单，具有较高的计算效率，但在强迫振荡模式分量提取中需要预先得到系统强迫振荡频率。此外，受故障类型和噪声影响，该方法容易对强迫振荡模式造成误判，振荡源定位精度不稳定。因此，如何准确辨识出广域量测信息中所隐含的强迫振荡模式信息，进而根据研究人员需求提取振荡模式分量定位振荡源，仍需进一步研究。

针对上述问题，本文在文献［16］基础上，提出一种基于连续小波变换（continuous wavelet transform，CWT）的强迫功率振荡源时频域定位方法。该方法首先将电力系统广域量测信息进行小波变换，然后通过小波相对能量实现电力系统强迫振荡模式分量提取；在此基础上，建立基于小波变换的DEF 计算模型，实现强迫振荡源的时频域定位；同时，计算振荡源定位量化指标以直观地展示强迫振荡源定位结果；最后，将所提方法应用到WECC 179 节点测试系统和中国辽宁电网中，进行分析、验证。

1 强迫振荡能量流

电力系统强迫振荡过程中，扰动源所激发出的暂态能量随着振荡不断变化，其包含的能量形式主要为势能和动能，基于经典发电机模型可得电网注入发电机的振荡能量如式（1）［16］所示：

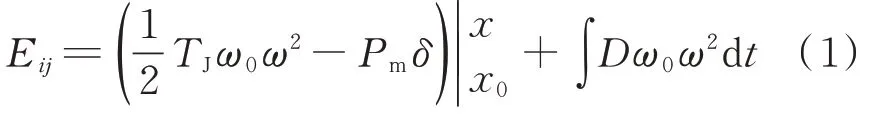
式中：Eij为节点j 注入节点i 处发电机的能量；ω 为发电机转速；ω0为转速基准值；δ 为发电机相角；TJ为发电机惯性时间常数；Pm为机械功率；D 为发电机阻尼系数；x0表示变量ω 与δ 的初始值；x 表示变量ω 和δ 的待定值；等式右边第1 项表示发电机暂态能量变化量，第2 项表示发电机耗散能量，该能量与发电机的阻尼系数相关，即向系统输出能量的发电机处于负阻尼运行状态。

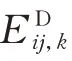
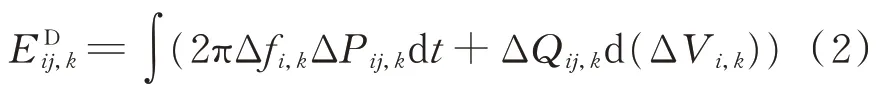
式中：ΔPij，k和ΔQij，k分别为线路Lij有功功率和无功功率偏差值的第k 个强迫振荡模式的分量；Δfi，k为节点i 频率偏差值的第k 个强迫振荡模式分量；ΔVi，k=Δln Ui，k为节点i 电压幅值自然对数偏差值的第k 个强迫振荡模式分量。

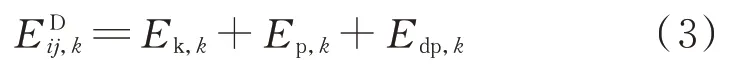
式中：Ek，k为第k 个强迫振荡模式下的支路动能；Ep，k为第k 个强迫振荡模式下的支路势能；Edp，k为第k 个强迫振荡模式的DEF，其上升或下降趋势可用于强迫振荡源定位。

根据式（2）和式（3）可计算系统流入发电机的DEF，并进行线性拟合Edp，k≈kdpt+cdp，其中kdp为拟合系数，cdp为拟合常数项。当kdp＜0 时，发电机处于负阻尼运行状态，即处于下降趋势的耗散能量曲线对应的发电机为电网的强迫振荡源［16］。

2 基于小波变换的电力系统强迫振荡模式分量提取

由第1 章可知，采用耗散能量定位系统振荡源时，需要首先从广域量测信息中辨识出系统的强迫振荡模式，进而再从所输入的广域量测信息中分离出含强迫振荡模式的时域量测信息分量，然后通过该分量计算各发电机DEF。为此，本章引入小波变换及其逆变换来分离出广域量测信息中所包含的强迫振荡模式时域量测分量。

2.1 小波变换

小波变换是一种时频域分析方法，它通过一系列小波基将广域量测信息在时域和频域中展开，实现信号的时频域分解。由文献［20］可知，对有功功率偏差值ΔPij进行小波变换后的小波系数矩阵WΔPij(a，b)为：

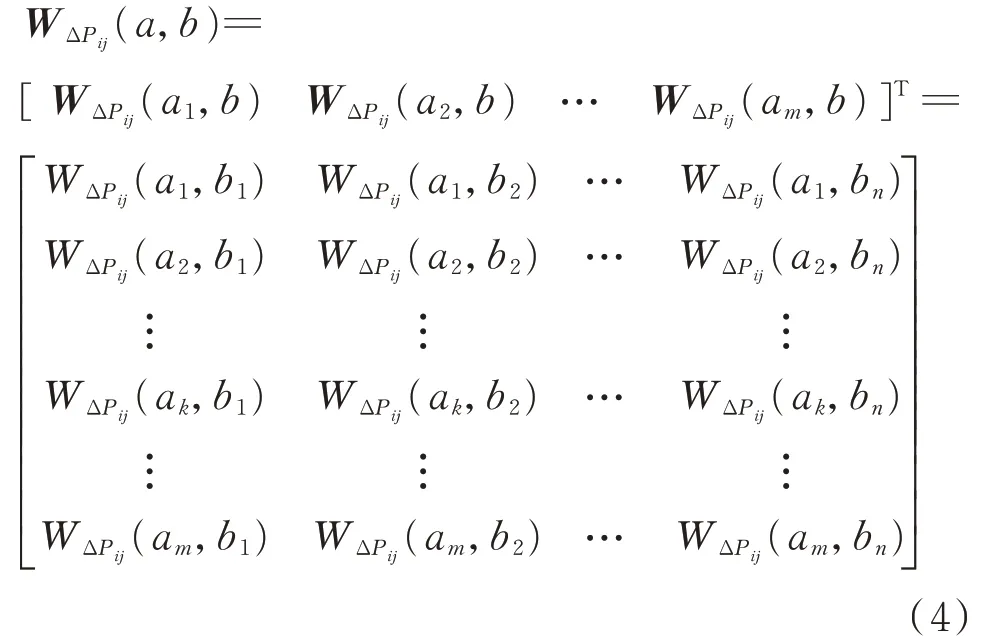
式中：a 和b 分别为小波变换的尺度系数和位移系数；WΔPij(am，bn)为ΔPij在小波尺度系数am和位移系数bn处的小波系数，其具体表达式如式（5）所示。

在式（4）所示的小波系数矩阵中，任一确定的尺度系数am在不同的位移系数bn下具有相同的振荡频率，即对应着同一振荡模式。

2.2 强迫振荡模式分量提取与重构

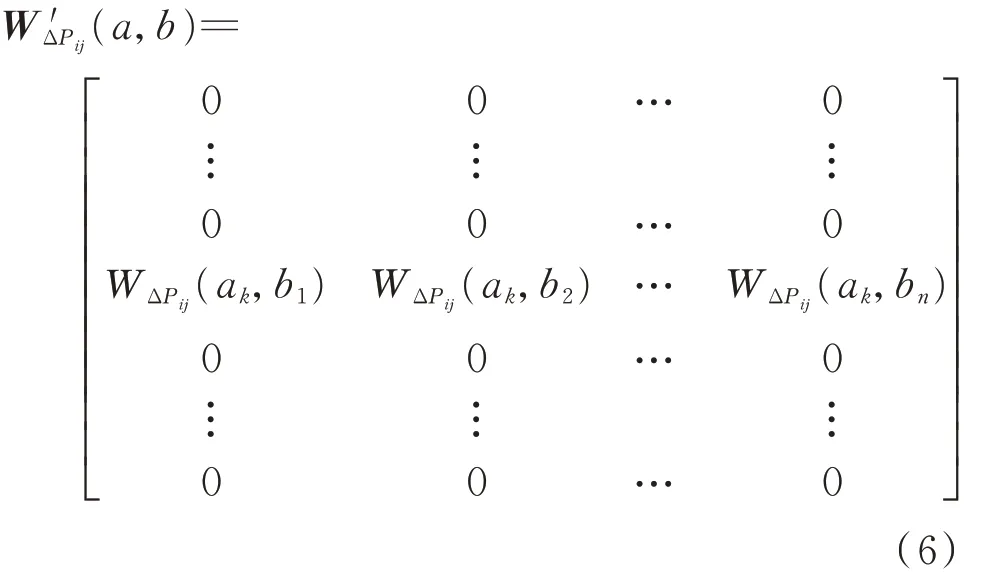
进一步，对式（6）所示的小波系数矩阵进行逆变换，即可得到仅包含强迫振荡模式信息的支路有功功率偏差值的时域分量：

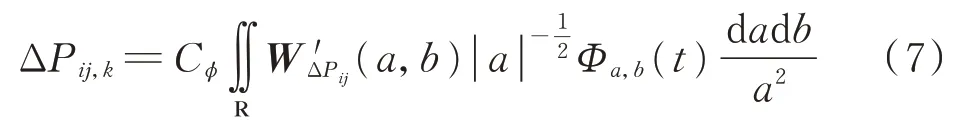
式中：Cφ为小波变换的容许常数，其表达式如式（8）所示。

同理，通过该方法可得ΔQij，k、ΔVi，k和Δfi，k。进一步，利用第1 章所提方法计算出发电机的耗散能量曲线，进而可定位出系统的强迫振荡源。

3 基于小波变换的强迫振荡源时频域定位

虽然基于小波变换的强迫振荡源时域定位方法可实现电力系统强迫振荡源的定位，但该方法相对繁琐，计算耗时久。为解决采用小波变换提取广域量测信息中强迫振荡模式分量的不足，本文进一步从时频域角度来剖析振荡能量的时空变化规律，以简化分析过程，实现强迫振荡源的定位。

3.1 强迫振荡能量流的时频域分析

由文献［14］可知，对于2 个已知的实信号x1（t）和x2（t），其CWT 有以下性质：

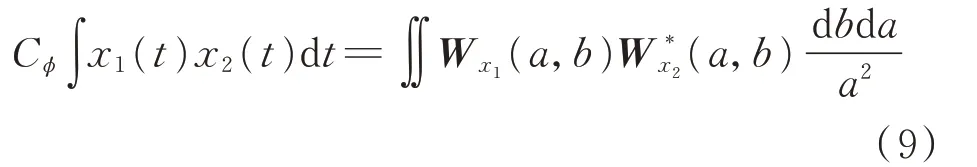
由于小波系数的幅值可表征信号的能量，结合式（2）和式（9），在时频域空间内，基于小波变换的支路振荡能量偏差值τDij可表示为：

若系统中仅存在某一强迫振荡模式，根据附录A 的推导，式（10）可进一步表示为：

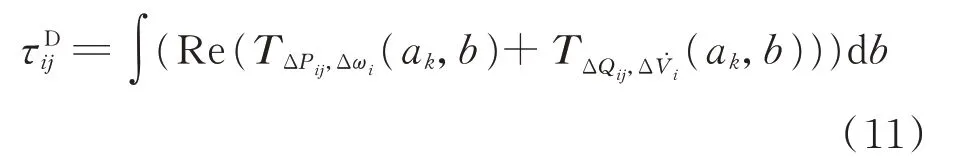
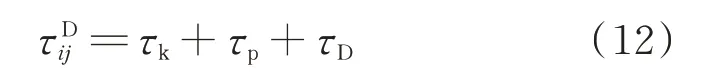
式中：τk为基于小波变换的支路动能；τp为基于小波变换的支路势能；τD为基于小波变换的支路耗散能量，对应于元件的阻尼特性，根据其曲线变化趋势可有效定位振荡源。

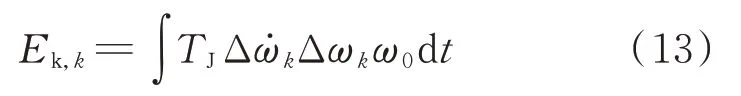
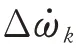
结合式（9）和式（13），当系统中仅存在某一强迫振荡模式时，τk可表示为：

实际系统中，τp具体表达形式不易获得。但根据能量一般具有二次函数形式的特点，τp可表示为τp=KΔxi2（K 为系数），对于单一振荡频率的振荡，有Δxi=Aeσtsin（ωt+ψ），因此τp可表示为：

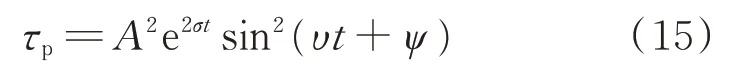
式中：σ、υ 和ψ 分别为信号特征值实部、角速度和初始相位角；A 为信号幅值。易知，τp为一个振幅不断变化的周期函数且其极小值点均为0。

根据暂态能量流的组成，可近似认为τD与τp+τD的极小值点相同，连接τp+τD的极小值点可近似获得发电机的耗散能量曲线。因此，基于小波变换的耗散能量与势能的能量和为：

假设c1和c2为τp+τD相邻的2 个极小值点，利用其差值判断支路的能量耗散可表示为：

综上，本文所提基于小波变换的强迫振荡源定位方法既揭示了振荡能量随位移系数b 变化的规律，也突出了其尺度系数a 的特征，体现了该方法的时频域特性。同时，该方法利用各电气量小波系数矩阵分析振荡能量，无须进行信号重构，可有效提高振荡源定位效率。

3.2 电力系统强迫振荡源定位的时频域分析量化指标计算

为定量分析各发电机对系统强迫振荡的影响，本节借鉴文献［9］的思路，在3.1 节的基础上，进一步定义了时频域空间中强迫振荡源能量流的量化指标，以准确定位系统的强迫振荡源，实现振荡源的快速识别，详细计算步骤如下：

步骤1：据3.1 节介绍的基于小波变换的DEF 定义，得到τp+τD曲线。

步骤2：提取出τp+τD曲线的极小值点数据。

步骤3：以输入数据总时长为时间区间，对极小值点进行最小二乘拟合，得到系数μ1、β，有拟合曲线T0（b）≈μ1b+β。

步骤4：同理，求取所有发电机的拟合曲线，得到各曲线的系数序列μ，求取序列μ 的极小值μmin，并将其作为基准值，对序列μ 进行归一化处理，得到强迫振荡源定位量化指标μ0。

步骤5：根据指标μ0定位系统强迫振荡源。μ0有以下性质：当μ0=1 时，表示该节点为强迫振荡源；当μ0≤0 时，表示该节点为正常运行状态；当0 ＜μ0＜1 时，μ0的数值越大，表明该节点对振荡的影响越大。

3.3 算法流程

综上，本文所提电力系统强迫振荡源的时频域定位方法流程如图1 所示。

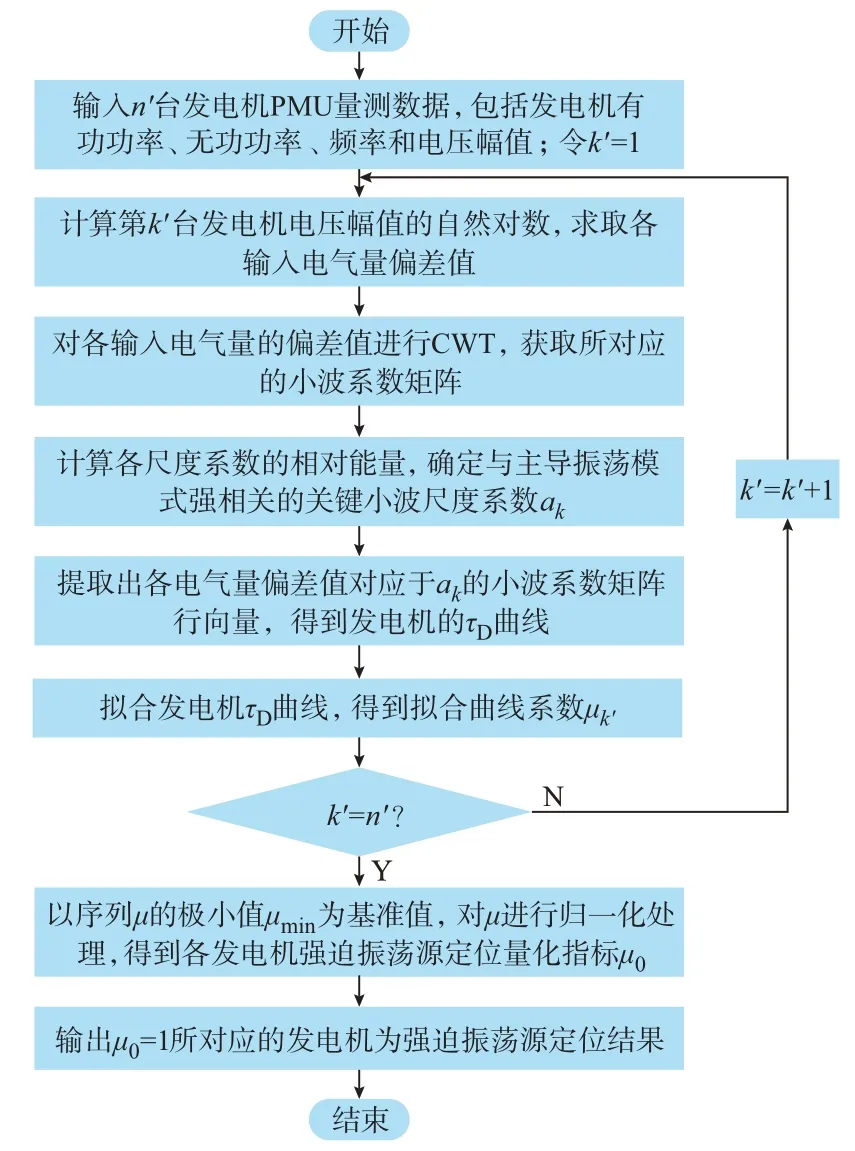
图1 强迫振荡源定位的时频域分析方法流程图Fig.1 Flow chart of time-frequency domain analysis method for location of forced oscillation source

详细步骤如下：

1）从PMU 中获取系统的广域量测信息，包括发电机有功功率、无功功率、频率和电压幅值。

2）计算电压幅值的自然对数，将各输入电气量减去初值求取偏差值。

3）根据式（5）对各输入电气量的偏差值进行CWT，获取所对应的小波系数矩阵。

4）计算小波系数矩阵中各尺度系数的相对能量，确定与强迫振荡模式对应的小波尺度系数ak。

5）提取出各电气量暂态量对应于ak的小波系数，结合式（16）和式（17）分析各发电机τD曲线的变化趋势。

6）拟合各发电机τD曲线，计算振荡源量化指标μ0，定位系统强迫振荡源。

4 算例分析

为验证本文所提方法的有效性和可行性，本章分别以WECC 179 节点测试系统和中国辽宁电网为例进行分析、验证。

4.1 WECC 179 节点测试系统

WECC 179 节点测试系统拓扑结构见附录B 图B1，系统参数详见文献［22］。设置发电机G74 为参考发电机，向发电机G79 的励磁系统持续注入振荡频率为0.46 Hz 的正弦信号作为强迫振荡扰动信号，持续时间为20 s。扰动期间各发电机的机端电气参数见附录B 图B2。

首先，以附录B 图B2 所示的各发电机机端电气量信息为输入，通过式（4）对图B2 中各发电机有功功率进行小波变换，共得到29 个小波系数矩阵。根据文献［21］所提方法，计算各小波系数矩阵中各尺度所对应的相对能量，设相对小波能量阈值R0=0.3。其中，发电机G65、G79、G116、G138 有功功率小波尺度系数的相对能量如附录B 图B3 所示。由图B3（a）可知，发电机G79 小波系数矩阵中各尺度相对能量出现1 个峰值，对应的尺度系数均为11，其相对能量为0.630 7，其他尺度的相对能量均低于0.3。由文献［21］可知：小波尺度系数的相对能量峰值对应系统主导振荡模式，因此可认为发电机G79的有功功率中存在1 组强迫振荡模式，对应的小波尺度系数为11，其相对能量为0.630 7。同理，由图B3 给出的发电机G79、G116 和G138 小波系数矩阵各尺度的相对能量可知：各发电机的有功功率中也存在1 组强迫振荡模式，对应的小波尺度系数均为11，相对能量分别为0.511 0、0.464 2 和0.552 4。进一步，根据文献［21］所提方法计算可得小波尺度系数11 对应强迫振荡模式的振荡频率为0.465 1 Hz，阻尼比为-0.28%，对比发电机G79 的励磁系统持续注入扰动频率可知：该强迫振荡模式的振荡频率与输入的扰动频率保持一致。因此，通过计算和对比各发电机有功功率的小波系数矩阵中各尺度系数的相对能量可得出：发电机G79 励磁系统注入的持续周期扰动激发出系统1 组强迫振荡模式，对应的小波尺度系数为11。分别从各发电机机端电气量信息的小波系数矩阵中提取出ak=11 对应的小波系数，结果如图2 所示，其中不同颜色曲线代表不同发电机。

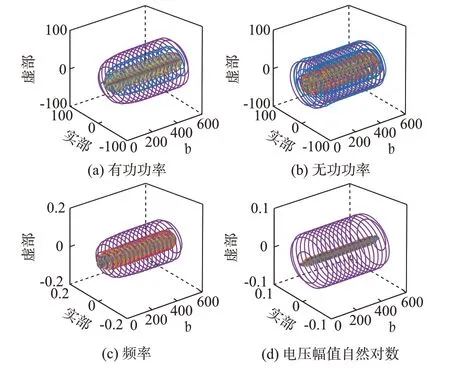
图2 ak=11 对应的电气量小波系数Fig.2 Wavelet coefficients of electrical parameters at ak=11

基于传统DEF 的强迫振荡源定位结果如表1所示，由该结果可知，发电机G79 为系统强迫振荡源，其余发电机对振荡无明显影响。

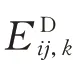
表1 基于传统DEF 的强迫振荡源定位结果Table 1 Forced oscillation source location results based on traditional DEF

图3 基于CWT 的发电机DEF 曲线Fig.3 CWT-based DEF curves of generators

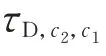
为定量分析各发电机对系统强迫振荡的影响，根据3.2 节所提方法将图3 所示各发电机τD曲线进行最小二乘拟合，得到拟合曲线系数μ1、β；求取系数序列μ 的极小值μmin，并将其作为基准值，对μ 进行归一化处理，得到强迫振荡源定位量化指标μ0；根据μ0取值得到的强迫振荡源定位量化指标值如表2所示。

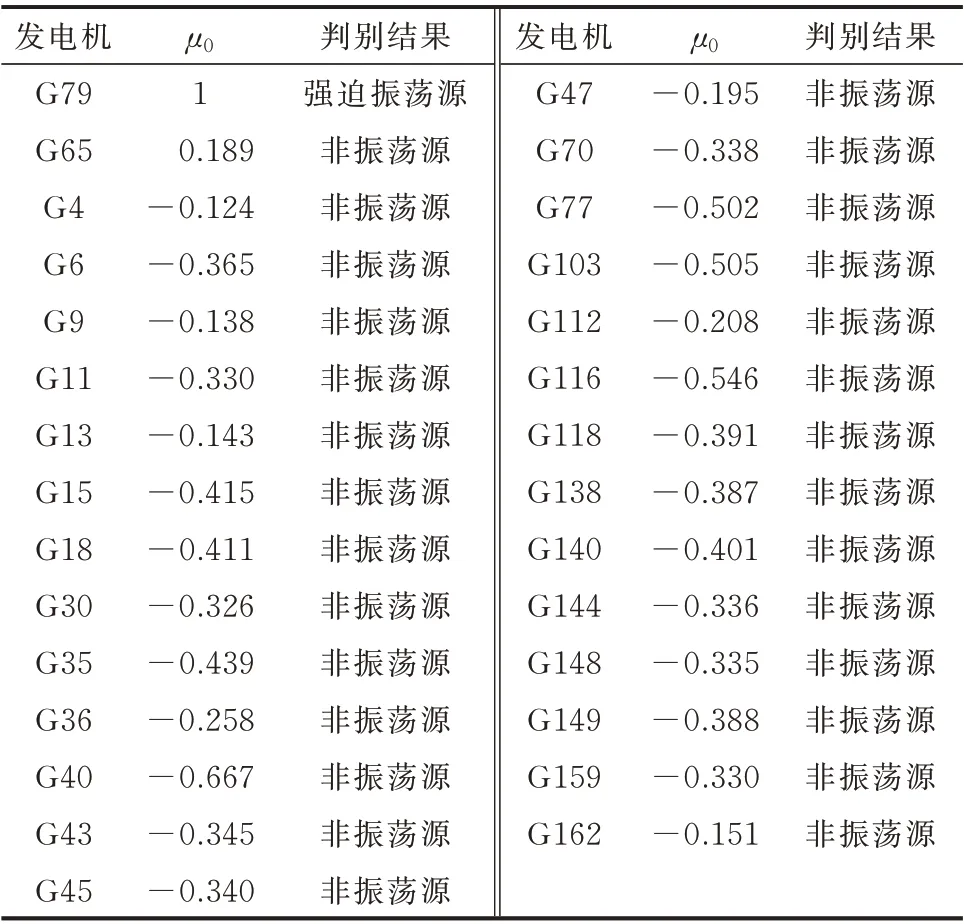
表2 强迫振荡源定位量化指标结果Table 2 Quantitative index result of forced oscillation source location

由表2 可知，发电机G79 的量化指标为1，为系统强迫振荡源；发电机G65 的量化指标为0.189，远小于发电机G79 的量化指标，对振荡影响较小；其余发电机量化指标均小于0，处于正常运行状态。上述分析结果表明：本文所提时频域定位方法与传统DEF 方法分析结果完全相同，验证了所提方法的准确性和有效性。

进一步对比传统DEF 与基于CWT 的DEF 计算时间（计算平台硬件配置为：CPU Intel Core i7-4710MQ，主频2.5 GHz，内存16 GB）。其中，传统DEF 计算时间为16.856 1 s，本文所提基于CWT 的DEF 计算时间为10.786 8 s，相较于传统DEF 计算耗时显著降低。上述结果表明：采用所提强迫振荡源时频域定位方法无须将各电气量的时频域信号重构为时域信号，可有效降低信号处理的复杂程度，提高强迫振荡源定位效率。

4.2 辽宁电网算例

4.1 节将本文所提方法应用于WECC 179 节点系统中验证其正确性和有效性，本节进一步以中国辽宁电网广域实测数据为例验证该方法在实际系统中应用的可行性。

2019 年5 月1 日，辽宁丹东热厂发生强迫功率振荡，振荡持续时间约为50 s。除丹东地区外，互联电网其他送电断面未发现明显的功率波动。由于全网机组众多，受篇幅限制，本节仅选取振荡源附近的丹东电厂、丹东热厂、大连湾火厂以及庄河火厂为研究对象，采用本文所提方法定位系统的强迫振荡源，全网振荡期间发电机机端参数振荡曲线见附录C 图C1 至图C4。

由图C1 至图C4 可知，本次振荡事件为典型的强迫功率振荡，具有起振快、振幅基本一致、振荡源未消除时振荡不能自行衰减的特点。以图C1 至图C4 所示各发电机的机端参数作为输入信号，对各发电机的有功功率进行小波变换，计算各小波系数矩阵中各尺度所对应的相对能量。各发电机实测有功功率小波尺度系数的相对能量见附录C 图C5，由图C5 可知，各发电机小波系数矩阵中各小波尺度系数相对能量共出现2 个峰值，对应的小波尺度系数分别为11 和22，对应的振荡频率分别为1.574 2 Hz 和0.040 1 Hz。滤除噪声影响并考虑低频振荡的研究范围为0.2～2.5 Hz，系统共有1 组强迫振荡模式，对应的小波尺度系数为11，振荡频率为1.574 2 Hz，阻尼比为0.457 3%。提取各发电机机端实测电气量信息小波系数矩阵中ak=11 对应的小波系数，结果如图4 所示，其中不同颜色曲线代表不同发电机。

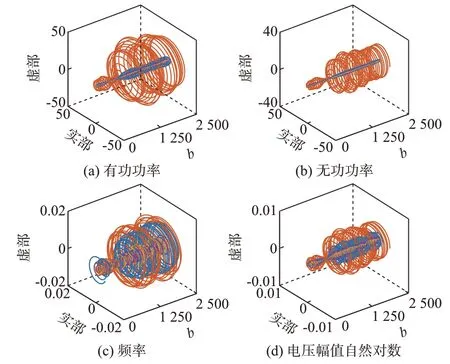
图4 丹东热厂强迫振荡中ak=11 对应电气量的小波系数Fig.4 Wavelet coefficients of electrical parameters at ak=11 in forced oscillation in Dandong thermal power plant of China

根据图4 所示各电气量ak=11 对应的小波系数重构各电气量的强迫振荡模式分量，结果见附录C图C6。根据图C6 所示各电气量强迫振荡模式分量，计算出各发电机耗散能量与势能和Edp，k+Ep，k，其极小值点连接曲线即为各发电机耗散能量Edp，k曲线，各发电机耗散能量曲线见附录C 图C7。

由图C7 可知，丹东热厂与丹东电厂对应的Edp，k曲线均呈下降趋势，其余发电机对应的Edp，k曲线呈上升趋势，则丹东热厂与丹东电厂的阻尼特性为负，此时段内该机组向系统注入能量；其余发电机对振荡起抑制作用；同时，相较于丹东电厂，丹东热厂对应的Edp，k曲线的下降趋势更为明显。因此，可判断出丹东电厂的负阻尼特性为位于丹东热厂的振荡源所激发，丹东热厂为系统强迫振荡源。

进一步，根据图4 所示各电气量ak=11 对应的小波系数计算基于小波变换的耗散能量与势能和τD+τp，其极小值点连接即为各发电机基于小波变换的耗散能量τD，各厂中发电机τD曲线如图5 所示。

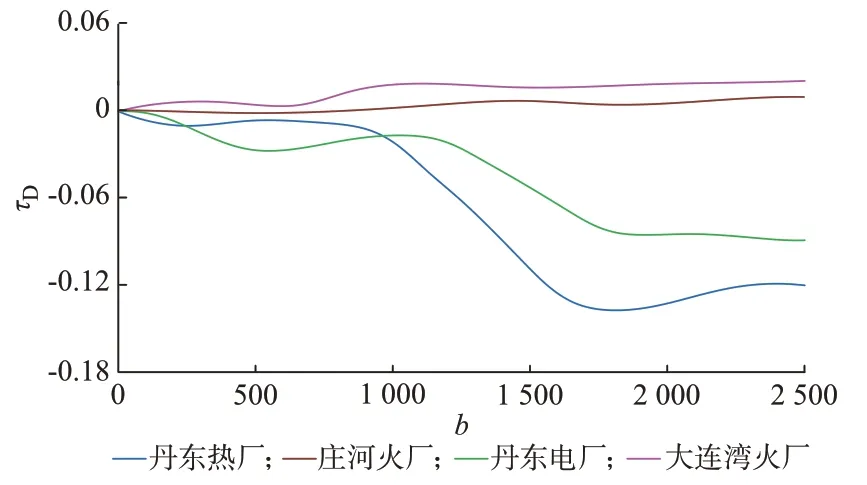
图5 丹东热厂强迫振荡中基于CWT 的发电机DEF 曲线Fig.5 CWT-based DEF curves of generators in forced oscillation in Dandong thermal power plant of China

为定量分析各发电机对系统强迫振荡的影响，根据3.2 节所提方法得到强迫振荡源定位量化指标如表3 所示。

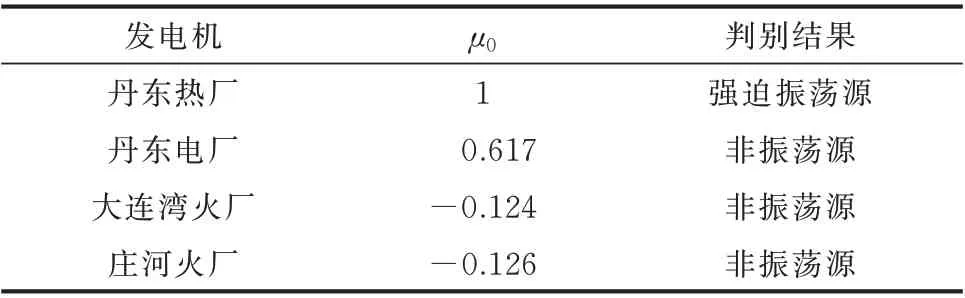
表3 丹东热厂强迫振荡事件中振荡源定位量化指标结果Table 3 Quantitative index result of forced oscillation source location in forced oscillation event in Dandong thermal power plant of China

由表3 可知，丹东热厂的量化指标为1，是系统的强迫振荡源；丹东电厂的量化指标明显小于丹东热厂，对振荡影响较小；其余发电机量化指标小于0，处于正常运行状态。

进一步，对比丹东热厂强迫振荡事件中不同方法的计算时间。其中，传统DEF 计算时间为1.719 7 s；本文所提基于CWT 的DEF 计算时间为1.072 3 s，相较于传统DEF 计算耗时减少。上述结果表明：相较于传统方法，本文所提强迫振荡源时频域定位方法的计算效率得到了有效提高。

综上，本文所提时频域定位方法与传统DEF 方法分析结果完全相同，符合2019 年5 月1 日辽宁丹东热厂强迫振荡的实际情况，验证了本文所提方法实现电力系统强迫振荡源定位的准确性和可行性。

5 结语

本文提出了一种基于小波变换的电力系统强迫振荡源时频域定位方法，将该方法分别在WECC 179 节点测试系统和中国辽宁电网实际系统中进行分析、验证。相较于传统DEF 的强迫振荡源定位方法，本文所提时频域定位方法不需要重构广域量测信息中所隐含的强迫振荡模式时域分量，有效提高了强迫振荡源的定位精度与定位效率。相对于基于时域或频域的强迫振荡源定位方法，本文所提方法从时频域角度来剖析振荡能量的时空变化规律，定位电力系统的强迫振荡源，为电力系统强迫振荡源的定位提供了新思路。

本文所提强迫振荡源定位方法尚未考虑扰动源的类型对定位结果的影响，后续工作将进一步研究不同扰动源下强迫振荡的区分与控制。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。