故障分量方向元件在交直流多端馈入系统中的适应性分析
2021-05-07宋国兵侯俊杰张晨浩吕江涛
宋国兵,常 鹏,侯俊杰,张晨浩,吕江涛
(西安交通大学电气工程学院,陕西省西安市710049)
0 引言
故障分量方向元件由于其原理简单、方向性明确,不受负荷和系统振荡影响等优点,广泛应用于交流线路保护中。其最佳应用场景是线性网络,在交直流混联系统中存在适应性问题[1-6]。
目前,针对故障分量方向元件在交直流混联系统中的适应性问题已有相关研究。文献[1,3]指出故障分量方向元件的最佳适用条件为系统正负序阻抗稳定,并对风电系统的阻抗特性进行了仿真分析;文献[7-8]通过电磁暂态仿真定性分析了换相失败对方向元件的影响;文献[2,9-11]结合实时数字仿真(RTDS)试验指出故障时换流器系统等值背侧正、负序阻抗相差较大,可能造成方向元件的误判;文献[12-14]则基于交流系统特性,建立了直流等值工频变化量阻抗模型,分析了换相失败和线路结构等因素对方向元件的影响。此外,文献[15]理论推导了换相失败期间电流开关函数表达式,通过电流暂态特性分析了换相失败对方向元件的影响;文献[16-20]则理论推导了逆变型电源等值序突变量阻抗表达式,进而分析了方向元件对不同逆变型电源的适应性。目前的研究主要集中于单馈入电网换相换流器(LCC)型高压直流(HVDC)输电系统和电压源换流器(VSC)型HVDC 输电系统,对故障分量方向元件在交直流多端馈入系统的适应性还缺乏系统性的研究。已有研究集中于探索换流器系统的阻抗特性,没有从故障分量方向元件动作特性方面研究其对换流器接入系统的适应性。
本文分析了故障分量方向元件的原理和动作条件。基于多条交流馈线和VSC 系统组成的交直流多端馈入系统,分析了方向元件判据与VSC 系统等值背侧阻抗波动区域的关系。结合换流器的故障响应特性,推导了VSC 系统等值背侧阻抗的变化范围,指出了影响方向元件适应性的因素,给出了故障分量方向元件在交直流混联系统的适用条件。
1 故障分量方向元件一般性适用条件
1.1 故障分量方向元件基本原理

对于图1(a)所示的常规系统,故障前后两端电源内电势和背侧阻抗可认为保持恒定。因此,图1(b)故障附加网络系统背侧阻抗与图1(a)中保持一致。下文将以此为基础,分析方向元件的动作条件。
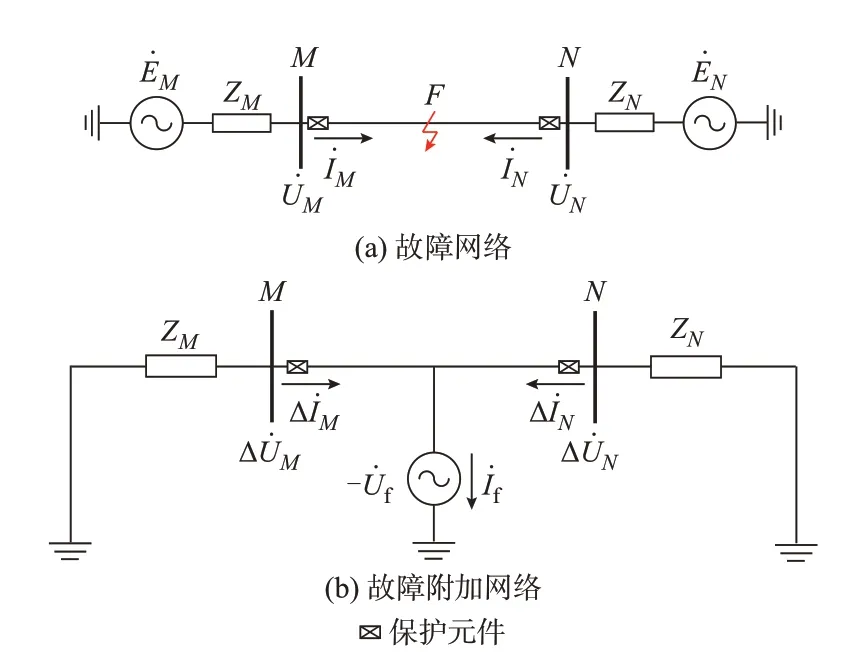
图1 常规系统故障网络分解图Fig.1 Decomposition diagram of fault network for conventional system
1.2 故障分量方向元件判据的整定
基于序故障分量的方向元件通过比较序电压故障分量和序电流故障分量之间的相位关系来判别故障方向,其实现形式包括正序故障分量、负序分量以及零序分量方向元件。由图1(b)可知,方向元件θj可表示为:

传统同步机系统背侧正负序阻抗可认为近似相等,且正负零序阻抗相角近似为90°,以正序故障分量方向元件为例,正方向故障时动作判据可表示为:

根据式(1)和式(2),故障分量方向元件判据的整定基于系统背侧序阻抗的性质,对于式(2)所示判据,方向元件的最佳动作条件为背侧序阻抗相角等于90°。因此,当系统背侧序阻抗性质发生变化时,方向元件存在适应性问题。
2 方向元件在交直流混联系统适用条件



图2 交直流多端馈入系统故障网络分解图Fig.2 Decomposition diagram of fault network for AC/DC multi-terminal infeed system
对于馈线1 中M 端的方向元件,换流器和馈线2 至馈线n 对应的交流系统均为系统背侧。当馈线1 发生故障时,M 侧保护安装处测得的阻抗ZM为Zd与ZΣ的并联。其中Zd(正序和负序)的取值随故障条件的变化而变化,在某些故障场景下呈容性[17],而ZΣ的值保持恒定。考虑到并联的定义,如果Zd的取值只能在确定的区域内变化,则一定存在对应的ZΣ,使方向元件满足式(2)的判据。
为了得到具有普适意义的结论,本文首先对ZΣ和不同阻抗并联得到的结果进行分析,以得到ZM取值和换流器等效阻抗Zd波动区域的关系。
2.1 保护安装处阻抗与换流器等效阻抗的关系
引入象限概念并结合图2(b)故障附加网络,有

式中:RΣ和XΣ均为大于0 的恒定值;Rd和Xd为波动值,可能位于4 个象限;AΣ、Ad、θΣ和θd分别为馈线阻抗和换流器等值系统背侧阻抗的幅值和相角。母线M 保护安装处对应的背侧阻抗ZM和阻抗角θM可表示为:

当ZM呈感性时,在直角坐标系中位于第1、第2象限;呈容性时则位于第3、第4 象限。因此,需要确定ZM所处象限与Zd波动区域的关系。求解式(5)和式(6),得到两者的关系如图3 所示,其中区域1 为平面内除区域2、3、4 之外的所有空白区域。

图3 θM 与Zd 的关系Fig.3 Relationship between θM and Zd
图3 中,区域2 和3 组成圆的半径为AΣ/(2cos θΣ),区域 3 和 4 组成圆的半径为AΣ/(2sin θΣ)。当Zd在区域1内波动时,θM∈(0°,90°);当Zd在区域2 波动时,θM∈(90°,180°);当Zd在区域3时,θM∈(-180°,-90°);当Zd在区域4 波动时,θM∈(-90°,0°)。
由上述分析可知,在ZΣ为恒定感性阻抗的条件下,对于式(2)判据,当Zd在图3 中区域1 和区域2 内波动时,方向元件不会误判。在此定义故障后方向元件不误判时Zd对应的区域为换流器背侧阻抗允许波动区域。由边界半径AΣ/(2sin θΣ)可知,当ZΣ的幅值较小,阻抗角接近90°时,Zd允许波动区域较大,方向元件正确判别的概率越高。
2.2 波动边界的整定
由2.1 节分析可知,对于式(2)所示的判据,Zd的允许波动区域为附录A 图A1 中黄色圆外的所有区域,因此Zd存在位于黄色圆边界上的波动临界值。根据正弦定理,Zd的临界值应满足:

求解式(7),可知式(2)判据方向元件不误判对应的波动临界条件为:

2.3 方向元件判据对允许波动区域的影响
为了更清晰地表明方向元件判据对Zd允许波动区域的影响,本文调整方向元件判别区间为(0°,φ),其中φ 为属于(90°,180°)的值,计算此判据下方向元件能正确判别时Zd的允许波动区域。方向元件不误判时,θM应满足式(9)。

式(9)所划定的边界为经过(0,0)和(-RΣ,-XΣ)2 个恒定点的圆,(0°,φ)对应判据下Zd的允许波动区域为附录A 图A2 中除区域2 和3 之外的所有白色区域。与图3 和图A1 对比可知,图A2 中区域2 部分为由于方向元件判据判别区间缩小而损失的Zd允许波动范围。若Zd只能在图A2 白色区域1内波动,则可将方向元件判别区间调整为(0°,φ)。同理,也可采用相同方法得到方向元件判据判别区间扩大时对应的Zd允许波动区域,并结合Zd的实际波动区域,对方向元件的判据进行调整。
综上所述,本章建立了故障分量方向元件判别区间与换流器等值背侧阻抗Zd波动区域之间的关系,定义了方向元件正确判别时Zd的允许波动区域,并推导了方向元件判据和ZΣ性质对Zd波动区域的影响,当Zd的实际波动范围在对应判据的允许波动范围内时,方向元件不会误判。需要指出的是,本文研究针对交流侧为多端的交直流多端馈入系统,当交流侧为单端时,本文研究结果并不适用。下文将结合换流器系统故障响应特性,对换流器系统等值阻抗实际变化范围进行推导,进而定量分析故障分量方向元件在图2 所示系统中的适应性。
3 逆变型电源等值序阻抗特性分析
附录A 图A3 为典型的逆变型电源接入电网示意图,其中逆变型电源采取两级升压并网的结构。箱式变压器(简称箱变)和主变压器(简称主变)的变比分别为kt1和kt2;Zt、Zl和ZT分别为箱变、汇集线路和主变的阻抗。考虑到箱变常见的电压等级为0.69 kV/35 kV 或0.69 kV/10 kV,主变常见的电压等级为35 kV/110 kV 或35 kV/220 kV,变比很大,因此,外部系统侧对应逆变站等值背侧阻抗Zd为:

式中:ZW为故障时根据逆变型电源出口电气变化量计算得到的背侧阻抗。
由式(10)可知,Zd可近似认为与ZW成正比。
与传统同步发电机电源不同,逆变型电源的输出特性与其控制策略密切相关,因此,下文将从逆变型电源的控制策略出发,研究其等值序阻抗特性。
3.1 等值正序阻抗特性
当外部系统发生故障时,逆变型电源一般采用双矢量控制策略以实现对正序、负序电流的单独控制。同时,为了实现低电压穿越,提升公共连接点(PCC)电压,VSC 系统应向线路注入一定的无功电流,由文献[21]可知,故障时PCC 正序电流的参考指令值可表示为:
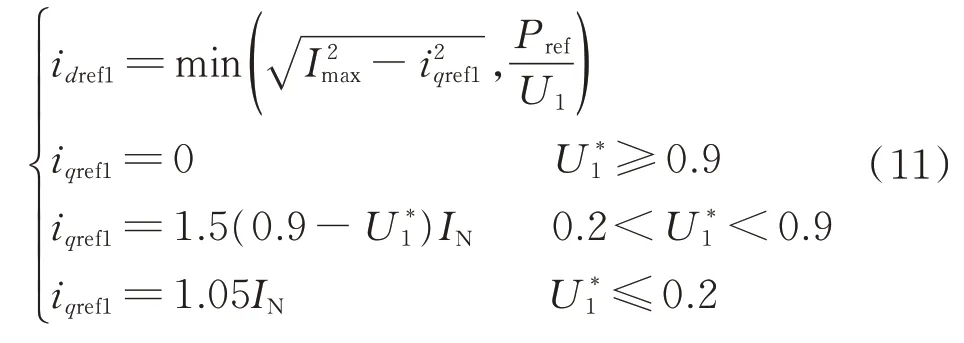

当VSC 系统运行在正常状态时,为了实现单位功率因数运行,VSC 的输出电压和电流保持同相位;而当系统发生故障时,由式(11)可知,正序电流超前正序电压的角度为:



根据故障分量方向元件的定义,换流器等值正序阻抗ZW1为:

由式(11)可知,故障期间逆变型电源出口正序电流仅为正序电压的函数,即VSC 可以等效为一个输出特性满足式(11)的压控电流源。结合式(10)、式(11)和式(14),对于特定的VSC 系统,等值背侧正序阻抗Zd1仅为ku和φu的函数,有

对于换流器系统来说,ku和φu的取值与多种因素相关,并没有确定的关系。考虑到换流器出口电压主要由所连接的交流系统支撑,因此故障前后换流器电压相位变化不会太大[22];同时,由于换流器的限流策略,当电压跌落很严重时,电流突变量仍很小,由式(10)和式(14)可知,此时Zd1幅值较大,对于探索式(8)对应的波动边界意义有限。为了能够应对继电保护关注的最恶劣情况,同时保证实际工程中的合理性,以换流站出口处线电压为额定值UN=380 kV,传输功率为500 MW 为例进行分析,设故障后ku∈(0.1,0.95),φu∈(-120°,60°),采用MATLAB对上述ku和φu范围内对应的Zd1幅值、相角进行求解,结果如图4 所示。

图4 VSC 等值背侧阻抗特性Fig.4 Characteristics of equivalent backside impedance of VSC
由图4(a)可知,Zd1在某些故障场景下呈容性,因此,在单馈入VSC 系统中正序故障分量方向元件并不适用。但对于特定的换流器系统,Zd1的实际波动范围是有边界的,其实际取值应包含于图4 中计算得到的等值阻抗范围中。将图4 中所有阻抗的取值映射在直角坐标系中形成的区域便包含了Zd1的实际波动区域,由于本文篇幅有限,且Zd1幅值较大时对探索式(8)对应的波动边界意义较小,本文仅列出Zd1幅值较小点的结果,如图5 所示,其中蓝色点为Zd1实际可能取到的波动点。

图5 等值正序阻抗实际波动区域Fig.5 Actual fluctuation area of equivalent positive sequence impedance
3.2 等值负序阻抗特性
当VSC 系统发生不对称故障时负序电流的取值与控制策略密切相关。由文献[22]可知不对称故障时VSC 系统输出的负序电流参考值可表示为:
当控制策略发生改变时,VSC 系统输出的负序电流特性也发生变化,对应的等值负序阻抗也不同,下文将结合控制策略,对VSC 等值负序阻抗进行分析。
3.2.1 抑制负序电流策略
由式(16)可知,当VSC 采用抑制负序电流控制策略时,系统输出侧负序电流为0,因此系统发生不对称故障时,换流器等值负序阻抗ZW2为:

3.2.2 抑制有功波动策略
当系统采取抑制有功波动控制策略时,换流器等效负序阻抗的幅值和相角表达式为[22]:

考虑到低电压穿越策略的要求,Pref和Qref均为正序电压幅值U1的函数,且有功参考值和无功参考值均为正值,kub∈(0,1),因此当系统采用抑制有功波动控制策略时,有
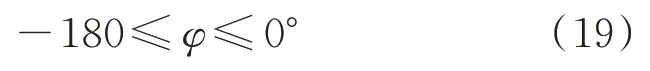
由式(18)和式(19)可知,在抑制有功波动控制策略下,系统发生不对称故障时VSC 等值负序背侧阻抗呈感性。
3.2.3 抑制无功波动策略
当VSC 采取抑制无功波动控制策略时,换流器等效负序阻抗的幅值和相角表达式为:

此时,有

由式(20)和(21)可知,在抑制无功波动策略下,系统发生不对称故障时VSC 等值负序背侧阻抗Zd2呈容性。与3.1 节等值正序阻抗的分析相似,Zd2可表示为U1和kub的函数,即:

为了能针对继电保护装置所关注的最恶劣情况,设故障期间U1的标幺值在0.1~0.9 p.u.变化,而电网不平衡度kub在0.1~0.9 范围内变化,同时考虑到故障后电压的幅值减小,增加约束条件如式(23)所示。

联立式(21)至式(23)求解,可得Zd2实际可能的波动区域如附录A 图A4 所示,图中蓝点形成的区域便包含了Zd2的实际波动区域。
3.3 等值零序阻抗特性
逆变型电源送出线路主变通常采用YNd11 接线方式,因此外部系统发生故障时,逆变型电源出口处没有零序回路,线路保护安装处对应的逆变站总等值阻抗仅为主变的零序阻抗,其相角接近90°,不受逆变型电源控制策略的影响,发生接地故障时系统的零序网络保持稳定[17]。
4 方向元件在交直流混联系统的应用分析
附录A 图A5 为本文所研究的逆变型电源接入电网示意图,下面将结合第2 章和第3 章所得结论,对方向元件在交直流多端馈入系统中的应用进行分析。
4.1 正序故障分量方向元件应用分析
对于图A5 所示系统,馈线1 发生故障时,M 侧保护安装处测得的正序阻抗ZM1为:
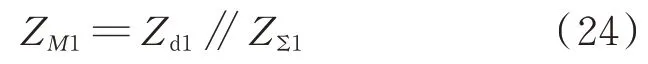
式中:ZΣ1为馈线等值正序阻抗。
根据第2 章和第3 章的分析,当一个恒定感性阻抗ZΣ1和一个容性波动阻抗Zd1并联时,如果ZΣ1满足式(8)的临界条件,正序故障分量方向元件便不会误判。而对于特定的VSC 系统,无论发生何种故障,Zd1都只能在图5 中实际波动范围内变化。因此,存在临界值ε 为:

式中:θd1为换流器正序阻抗相角。
当ZΣ1满足AΣ1/sin θΣ1<ε 时,保护安装处的正序故障分量方向元件便不会误判。而当上述条件不成立时,以式(2)为判据的方向元件存在误判的可能性,这种情况下可以根据2.1.2 节所述实际波动区域与判据的关系,修正方向元件的判据。
将图5 中Zd1在波动区域对应的实际取值代入式(25),通过MATLAB 求解得到,对于此VSC 系统,临界值ε=144.96。因此,当馈线1 发生故障时,只要满足AΣ1/sin θΣ1<144.96,M 侧保护安装处的方向元件便不会误判,此时Zd1的实际波动区域与允许波动区域的关系如图6(a)所示。图中,蓝点为Zd1实际可能的波动点,白色区域为根据ZΣ1划定的允许波动区域,黄色区域为误动区域。反之,当实际波动区域和误动波动区域有交集时,如图6(b)所示,正序故障分量方向元件存在误判可能。

图6 方向元件适应性分析Fig.6 Adaptability analysis of directional elements
4.2 负序方向元件应用分析
当图A5 中馈线1 发生不对称故障时,保护安装处测得的等值负序阻抗ZM2为:


当系统采用抑制负序电流控制时,Zd2可近似为无穷大,代入式(26),此时ZM2可以近似等于馈线负序阻抗ZΣ2,由于ZΣ2为感性恒定阻抗,因此负序方向元件不会误判。
当系统采用抑制有功功率控制时,由式(18)可知此时Zd2呈感性,代入式(26)可知ZM2呈感性,因此负序方向元件不会误判。
当系统采用抑制无功功率控制策略时,由式(20)可知此时Zd2呈容性,可采用与4.1 节相同的方法对其适应性进行分析,本文不在此赘述。
4.3 零序方向元件应用分析
由3.3 节的分析可知,当逆变型电源送出线路主变采用YNd11 接线方式时,发生接地故障时逆变站总等值阻抗仅为主变的零序阻抗ZT0,此时保护安装处测得的零序阻抗ZM0为:
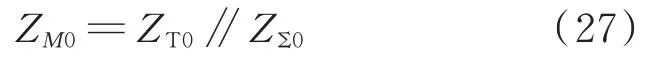
式中:ZΣ0为等值馈线零序阻抗。
ZT0和ZΣ0均为相角接近90°的恒定阻抗,因此零序方向元件不会误判。
4.4 影响因素分析
4.4.1 换流器系统容量
由式(14)和式(25)可知,对于特定的VSC 系统,临界值ε 与UNIN成正比,即:

根据第3、第4 章所述方法计算不同功率VSC系统对应的临界值ε,结果如表1 所示。当换流器系统容量增大时,在同一电压等级下输出电流的能力增强,换流器等效背侧阻抗幅值减小,但相位仍然可能呈现容性,因此临界值ε 也减小,如果馈线阻抗幅值较大,故障分量方向元件可能存在不适应问题。
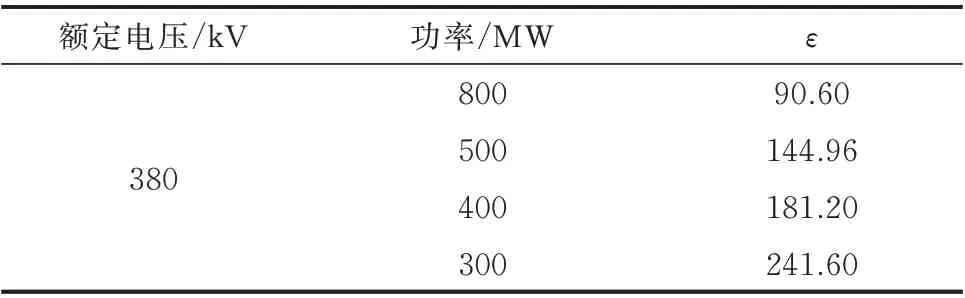
表1 不同功率下ε 值Table 1 ε with different power
4.4.2 馈线交流系统强度
对于特定的VSC 系统临界值ε 是确定的,当馈线交流系统强度增大时,馈线阻抗ZΣ的幅值减小,当馈线交流系统强度大于临界系统强度时,方向元件便不会误判。
4.4.3 系统控制策略
由本文3.2 节和4.2 节可知,当逆变型电源的控制策略发生变化时,换流器等值阻抗的波动范围也发生变化,方向元件的适应性分析需要考虑换流器的控制策略。
5 仿真验证
为验证本文对传统方向元件适应性分析理论的正确性,在PSCAD 软件中搭建了如附录B 图B1 所示的VSC 逆变站仿真模型。模型参数为:VSC 容量为500 MW;主变容量为1 500 MW;额定电压变比为380 kV/230 kV;短路阻抗比10%;接线方式为YNd11;系统侧电压等级为380 kV;馈线的线路长度均为50 km。馈线正序参数为:r1=0.053 Ω/km,l1=1.081 mH/km,c1=0.013 2 μF/km;零序参数为:r0=0.291 Ω/km,l0=2.74 mH/km,c0=0.008 9 μF/km。馈线1 对应的交流系统等值正序背侧阻抗ZN1为(2.43+j54.35)Ω;馈线2 则用集中参数模型表示,ZΣ的取值待定,当改变ZΣ取值时,调整交流电动势使VSC 运行在额定工作状态。
由于已有大量文献对负序方向元件和零序方向元件在VSC 系统中的应用进行了研究[2,18],且上述2 种方向元件不能反映所有的故障类型。因此,本文主要对正序故障分量方向元件在图B1 所示系统中的适应性理论分析进行仿真验证。
5.1 换流器等值正序阻抗特性验证
为验证3.1 节换流器等值正序阻抗特性的正确性,取ZΣ为(16.40+j96.35)Ω,在附录B 图B1 所示馈线1 中设置不同类型和过渡电阻的故障,故障持续时间为0.1 s,仿真采样频率为10 kHz,采用全波傅里叶算法计算直流逆变侧等值正序阻抗。本文仅给出部分故障场景下线路MN 中点发生三相接地故障时换流器系统的等值正序阻抗,如附录B 图B2 所示。取故障发生时刻为0 ms,考虑全波傅里叶变换至少需要1 个工频周期的数据窗,因此正序阻抗的计算结果从20 ms 显示。
图B2 中3 种不同的曲线分别表示了过渡电阻为30 Ω,50 Ω 和100 Ω 时换流器等值正序阻抗仿真值。对比图B2 所示换流站等值正序阻抗的仿真结果与图5 中理论推导得到的实际波动区域,可知故障发生后换流站等值正序阻抗Zd1的确位于图5 的实际波动区域之中,与3.1 节理论分析结果一致。
5.2 正序故障分量方向元件适应性验证
由4.1 节可知,对于电压等级为380 kV、传输功率为500 MW 的VSC 系统,临界值ε 为144.96。调整ZΣ的取值,对其值为(16.40+j96.35)Ω 以及(67.6+j385.4)Ω 时M 侧方向元件测得的背侧阻抗进行仿真计算,在改变ZΣ取值的同时,调整交流电动势使VSC 运行在额定工作状态。由上文分析可知,第1 组ZΣ的取值小于临界值,因此M 侧方向元件一定不会误判;而第2 组ZΣ的取值大于临界值,M侧方向元件存在误判可能。由于篇幅有限,本文仅给出部分故障场景下M 侧方向元件测得的背侧阻抗相角仿真值,如附录B 图B3 所示。
图B3(a)为线路MN 中点发生过渡电阻为100 Ω 的三相对称故障时M 侧保护安装处测得的背侧阻抗相角;图B3(b)为线路MN 中点发生过渡电阻为30 Ω 的三相对称故障时M 侧保护安装处测得的背侧阻抗相角;图B3(c)为线路MN 中点发生过渡电阻为10 Ω 的B 相接地故障时M 侧保护安装处测得的背侧阻抗相角。
由图B3 可知,在上述故障场景下,ZΣ取值为(16.40+j96.35)Ω 时,M 侧方向元件测得的背侧阻抗呈感性,不会误判;而当ZΣ取值为(67.6+j385.4)Ω时,如图B3(c)所示,系统发生B 相接地故障(BG)时M 端测得正序阻抗呈容性,方向元件可能误判。当ZΣ小于VSC 对应的临界值时,仍可采用式(2)判据的故障分量方向元件;当ZΣ大于临界值时,则可根据换流站阻抗的实际波动区域,结合2.1.2 节的内容尝试对方向元件进行修正,若换流站阻抗的实际波动区域和误动区域存在大量重叠区域,且无法修正判据,则故障方向元件不能在此交直流多端馈入系统使用。
6 结语
本文基于故障分量方向元件原理,研究了元件的动作条件,并推导了交直流多端馈入系统中方向元件动作区间与换流站等值背侧阻抗波动的关系。提出了一种故障分量方向元件在交直流多端馈入系统适应性的分析方法。
对于交流侧为多端的交直流馈入系统,可以根据馈线阻抗和方向元件判据划定馈线侧方向元件不误判时对应的换流站等值背侧阻抗允许波动区域,并根据换流器的参数和控制策略,求解换流站等值背侧序阻抗的实际波动区域。当换流器等值背侧阻抗的实际波动区域完全位于对应判据下的允许波动区域时,方向元件不会误判。因此,可以结合不同方向元件判据下对应的允许波动区域,定量分析正序故障分量方向元件和负序方向元件在交直流多端馈入系统的适应性。而对于零序方向元件,当换流器送出线路主变采用YNd11 接线方式时换流站等值零序阻抗保持稳定,零序方向元件不会误判。
由于本文所研究的拓扑结构要求交流为多端,当交流为单端时,无法求解换流器背侧阻抗的允许波动区域,此时本文所提出的适应性分析方法并不适用;另外,当交直流多端馈入系统拓扑结构发生变化时,需要实时定量分析故障分量方向元件的适应性以自适应电网拓扑结构的变化。在交直流混联电网中,不受电网拓扑结构和系统参数影响的方向元件还有待进一步研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
