多能源枢纽联合运行的㶲损最小化分布式优化调度

2021-05-07盛超群雷金勇

电力系统自动化 2021年9期

何帅，刘念，盛超群，雷金勇

（1. 新能源电力系统国家重点实验室（华北电力大学），北京市102206；2. 国网浙江杭州市萧山区供电有限公司，浙江省杭州市311200；3. 南方电网科学研究院有限责任公司，广东省广州市510663）

0 引言

随着环境、能源等问题的日益紧迫以及负荷需求的不断增加，能源利用效率亟待提高［1-2］。整合多种能源的能源枢纽（energy hub，EH）概念［3］应运而生，EH 通过内部设备，将输入能源按照负荷需求高效地进行转化，从而提升能源系统运行效率［4］。

目前，在多EH 联合优化运行研究中，文献［5］提出在动态能源价格和需求响应的基础上，将多EH 作为潜在主体，与能源公司进行博弈，来优化各EH 的运行成本，文献［6］考虑光伏出力与负荷随机性以及枢纽管理者（hub manager，HM）与光伏产消者之间的合作，采用滚动时域的方法对负荷需求进行合理调度，文献［7］提出了一种含多个EH 的综合能源系统基本框架，构建了计及碳排放的分布式日前低碳经济调度模型。

现有文献大多仅以成本最低为目标，而本文在模型中引入了㶲的概念。㶲是基于热力学第二定律建立的热力学参数，其定义为在确定的环境条件下系统经可逆过程达到与环境相平衡的状态，能够对外界所做的功［8］。㶲损体现了在满足同等生产生活需要的前提下，消耗的可利用能源，因此以㶲损最小为目标，可以有效提高能源利用效率。目前已有部分学者围绕㶲与多能联产系统展开研究。文献［9］通过㶲分析为多能源互补和梯级利用的能源系统集成提供了新方法。文献［10］利用㶲效率对其烘干利用系统平台进行了性能分析。文献［11］将㶲利用率作为一个重要指标对多能互补能源系统的能效水平进行了评价。文献［12］将电网络理论中的基尔霍夫定律推广至适合于能量网络建模的广义基尔霍夫定律，然后以能量（㶲）在线（管）路中的传递特性方程为基础，推导出普遍化的集中参数等效传递方程，再将所得到的方程统一为能量网络方程组并论证了其可解性。然而，在多EH 的优化运行中考虑㶲这一概念的研究还较少，本文以㶲损最小为目标，从而实现通过合理的调度实现减小能耗与提高能源利用率的目的。

优化模型求解也是核心内容之一，可分为集中式与分布式求解。其中分布式求解算法包括辅助问题原则（auxiliary problem principle，APP）法、交替方向乘子法（alternating direction method of multipliers，ADMM）、最优性条件分解（optimality condition decomposition，OCD）等［13-15］。本文中各EH 分属不同运营商，若采用集中式求解，一种解决方案是各个运营商将其内部的设备信息发送给某一运营商，由其以全局最优为目标制定运行方案，而这不利于保护各运营主体的商业隐私，另一种解决方案是由独立的第三方运营商收集各运营商内部的设备信息，并进行运行方案的制定，而这涉及第三方运营商的相关政策制定及商业模式问题。而采用分布式求解算法，各EH 运营商仅需提供“期望交换功率”，有利于保护各运营商的商业隐私，减少整体的通信传输以及保证调度的相对独立性。同时，ADMM 方法数学推导严谨，并且只需交换少量信息便能实现全局优化，具备收敛精度高、信息传输量小、计算速度快等优点［16］。因此，本文采用ADMM对优化模型进行求解。

综上，本文主要贡献如下：①以㶲损最低为目标，建立了多EH 联合优化运行调度模型；②基于温度变化范围较小的前提，将热量㶲近似为温度的线性函数，进而将热量㶲转化为热力功率的线性函数，降低了求解难度；③通过ADMM 分布式优化算法进行求解，各EH 间仅交换部分信息，更好地保护EH 的隐私。

1 EH 及㶲值计算模型

1.1 EH 结构

在配电网中存在若干个EH，如图1 所示。每一个EH 由HM、电力负荷、热力负荷、分布式光伏发电系统以及热电联产（combined heat and power，CHP）系统组成。

图1 含多EH 的配电网示意图Fig.1 Schematic diagram of distribution network with multiple EHs

在传统独立运营模式下，各EH 由不同的HM进行调度，每个EH 输入电能与天然气，自身光伏发电与从电网购得电能满足EH 内电负荷需求；CHP机组消耗天然气，产生电能与热能，供给EH 内电热负荷需求，多余电量上网。

1.2 能量/能源㶲值计算模型

如图2 所示，在工程中，㶲流［8］可以分为：输入㶲流（指外界的㶲源，物流穿过系统边界而进入系统的供给㶲，如燃料㶲、电㶲等）和输出㶲流（是指由系统边界向外输出的㶲）。输入㶲经过EH 中CHP 机组等的转换成为电热等输出㶲供给负荷。生产和转换过程中在机组内部及供给过程中散失到环境中的㶲减少量为㶲损。

图2 㶲流分类Fig.2 Classification of exergy flow

1.2.1 EH 燃料㶲模型

EH 中输入的燃料㶲主要用于CHP 系统，CHP系统可以将输入的燃料转化为电能和热能提供给用户，其电功率与热功率满足以下关系［17］：

CHP 系统消耗天然气与产出之间的函数关系为：

工程计算中，天然气的燃料㶲值［8］可以表示为：

1.2.2 EH 与电网交易电量㶲模型

EH 与电网存在电能交易，当EH 内CHP 系统以及光伏发电量不满足电负荷需求时，需从电网购买电量；反之，EH 内发电量超过电负荷需求时，多余部分电量可以出售给电网获取一定收益，则EH与电网交易电量的㶲值可以表示如下。

当EH 购买电网电能时，由于电网电能是由煤炭等一次能源转换而来，所以根据积累㶲理论，可以将从电网购入电能按照一定比例折合成化石燃料耗量（标准煤消耗量），并计算出EHi所购买的电网电能的㶲值［8］，其公式如下：

当EHi向电网售出电量时，根据电量㶲的计算方法［8］，可得上网电量㶲值为：

1.2.3 光伏电能㶲值计算模型

EH 内的光伏设备利用光伏效应，将太阳能直接转换为电能，光伏设备输出的电能㶲值的公式如下：

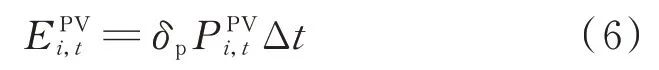
1.2.4 负荷㶲值计算模型

1）电负荷㶲计算模型

EH 内用户电负荷的㶲值可根据电量㶲的计算方法［8］进行计算，其公式如下：

2）热负荷㶲计算模型

本文热负荷主要考虑温控负荷，通过计算最终用户室内介质获得的㶲值，作为EH 内用户的热负荷㶲值。热量㶲的定义为温度高于环境温度的系统在给定环境条件下发生可逆变化时，传递的热量所能对外做出的最大有用功［8］，其计算公式如下：

式中：EH为热量㶲；T0为环境温度；T 为介质温度；C为介质比热容。

因此，介质的热量㶲为温度T 的函数，由于本文考虑的介质为用户室内的空气，其温度一般需要维持在相对较小的范围（Tmin～Tmax）内，如20～25 ℃。在温度变化范围较小时，介质的热量㶲可近似为温度T 的线性函数，通过线性回归，即可求得热量㶲在一定温度范围内的近似线性函数，其公式如下：

式中：δh为热量㶲对温度变化的近似系数；δb为线性回归函数的截距。

因此，当介质与外界交换了热量Q，温度由T1变化至T2时，则介质热量㶲的变化量可用下式表示：

式中：ΔEH为介质热量㶲的变化量。

因此，对于EH 内用户的热负荷㶲值，即用户室内介质热量㶲的变化量，可用下式表示：

1.2.5 交换电量、热量的㶲值计算模型

1.2.6 换热器㶲损计算模型

换热器是一种在不同温度的2 种或2 种以上流体间实现物料之间热量传递的设备，其㶲损为输入㶲减去输出㶲，输入、输出的热量㶲根据式（8）即可求得，其具体公式如下：

由于本文优化目标是系统整体的㶲损最小，即系统整体的输入㶲和输出㶲的差值最小，换热器的输入㶲和输出㶲均为中间过程，因此换热器的㶲损模型在目标函数中没有体现，但是换热器的效率大小会影响到系统整体的㶲损大小，其体现在EH 与热网交互热功率约束中。本文引入换热器的㶲损模型主要目的是在后面的算例分析中，对系统内㶲损分布进行分析时，可以对换热器的㶲损进行计算。

2 多EH 㶲损最小化优化调度模型

2.1 目标函数

位于同一能源配送网络中的多个EH 之间友好合作，通过电量与热量的互动，实现整体㶲损最小化的优化调度目标。

对于单个EH 而言，在其生产、转换与供应过程中，输入㶲包含CHP 系统所需的燃料㶲、从电网购电折合消耗的标准煤㶲、光伏产生的电能㶲，输出㶲包含供给内部用户的电负荷㶲、热负荷㶲、上网电量㶲以及与其他EH 交换的电量和热量㶲。通过输入㶲与输出㶲的差值，可以获得EHi的㶲损。

因此，单个EH 的㶲损可用下式表示：

式中：fi(xi)为EHi的㶲损；xi为EHi内部的决策变量；Tt为时间段数。

因此，多EH 㶲损最小化优化调度模型的目标函数为各个EH 的㶲损之和，其公式如下：

式中：ftotal为多EH 的总体㶲损；N 为EH 的数量。

2.2 约束条件

EH 在运行时，其内部需满足一定的约束条件，具体表达式如下。

1）电功率平衡约束

2）用户室内温度约束

根据热负荷与温度模型［18］可得，用户室内温度与热量供应的关系为：

用户室内温度的上下限约束如下：

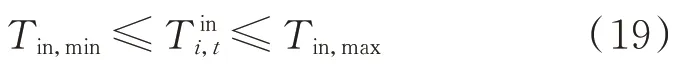
式中：Tin，min为用户室内可接受的最低温度；Tin，max为用户室内可接受的最高温度。

3）CHP 机组运行约束

CHP 系统电功率与热功率比例约束如下：

CHP 系统电功率上下限约束如下：

CHP 系统电功率爬坡约束如下：

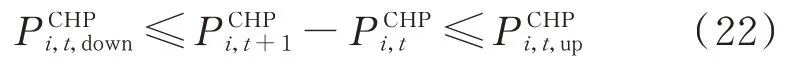
4）EH 向电网购售电约束

上述约束表明购电功率与售电功率至少有一个为零，即不能同时购电和售电。由于购电的单位㶲值大于售电的单位㶲值，当购电功率与售电功率同时大于零时，其相当于增加了系统的㶲损，不符合最小化㶲损的目标。因此，式（24）的约束并不起作用，可以将其删去，从而简化优化模型。

5）EH 与电网交互电功率约束

EH 与电网交互电功率由3 个部分构成，即售电功率、购电功率以及EH 之间的交互功率，其大小受限于EH 与电网相连的联络线的传输功率上下限，具体如下：

6）EH 与热网交互热功率约束

式中：ηhe为CHP 机组输出高温水与热网低温水间换热器的热效率。

此外，各个EH 还需满足一定的能源网络约束，包括以下几个方面。

7）电交互功率平衡约束

8）热力网络平衡约束

对于热力网络中的每一个节点，与其相连线路的总注入热功率为零，即

式中：Hl，m，t为热力网络中与节点m 相连的线路l 的热功率，注入节点功率为正；ψ(m)为与节点m 相连的线路集合。

对于热力网络中的每一条线路，由于热力传输过程中存在一定的延时，线路首端的热功率与末端的热功率存在一定的时差，其具体公式如式（29）所示［19-20］。

式中：Δtd，l为线路l 传递热量的延迟时间；Kd，l为线路热延时系数，其为一常数，与线路自身的参数相关；Ll为线路l 的长度；ul为线路内工质流动速度。

同时，热力传输过程中也存在一定的损耗，可用常数进行近似，其具体公式如式（30）所示［21］。

式中：ΔHl为线路l 的热力损耗；Tsw为热网的供水温度；Rl为热力线路l 热媒到周围介质间每千米管道的总热阻。

因此，线路首末端的热功率需满足下述约束：

式中：min和mout分别为线路l 的首端节点和末端节点。

一个时间序列延时Δtd，l后，时间序列延时前后的关系如下：

式中：X（t）为时间尺度为1 h 的时间序列；［·］为取整运算。

同时，由于热力网络中的工质流动存在一定的方向，一般只能从首端流向末端，即

3 基于ADMM 的分布式求解算法

ADMM［22］自20 世纪70 年代被提出以来，现已广泛应用于求解大规模分布式优化问题，在含CHP系统的综合能源系统优化运行方面也有所应用。

本文采用ADMM 对前文所提模型进行求解，需将所建立的模型转化为ADMM 标准型。

首先，由前文可知，EH 总㶲损由各个EH 的㶲损之和构成，因此其符合ADMM 的标准型。

其次，确定各个EH 内部的优化变量Xi的范围，对于单个EH，其优化变量包括CHP 系统电热功率、与电网间的购售电功率、与其他EH 交互的电功率、热功率、热力网络中与其接入点相连的线路功率。

最后，确定各个EH 之间的耦合等式约束，模型的优化变量中，涉及多个EH 内部变量的等式约束包括电功率交互功率平衡约束和热力线路首末端功率延时约束。

因此，前文所建立模型可以转化为ADMM 标准型，其增广拉格朗日函数如下：

式中：ρ 为惩罚系数；hi(xi)为拉格朗日增广函数的附加项。

由前文所建立的模型可知，原集中式优化模型为线性模型，因此转化为ADMM 分布式求解后，每次迭代为求解一个二次规划问题，其属于凸优化的范畴，求解较为容易。

因此，基于ADMM 的㶲损最小化分布式优化算法的迭代过程如下。

对于每个EH，其内部优化模型如下：

约束条件为式（17）—式（23）、式（25）—式（28）、式（31）以及式（33）—式（34）。

由前文可知，各个EH 的㶲损函数及其约束条件均为线性模型，因此其可以通过ADMM 进行有效的求解。

拉格朗日乘子的更新公式如下：

因此，可得残差最大值如下：

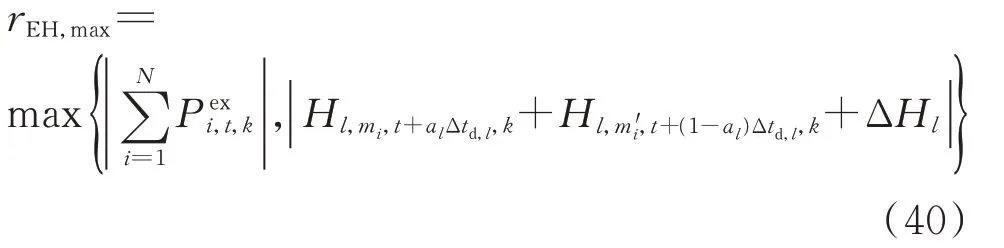
式中：rEH，max为所有残差中的最大值。

算法的收敛条件为：

式中：ε 为残差收敛精度。

在算法优化的初期，为了加强算法的全局搜索能力，避免过早地满足收敛条件而停止继续寻优，因此设定了一个最小迭代次数Niter，min，当迭代次数小于Niter，min时，算法不会因满足收敛条件而停止迭代。

综上，各EH 的HM 以自身㶲损和附加项之和为优化目标，对自身内部的决策变量进行优化，从而更新自身的优化变量，所有EH 均优化完成后，更新拉格朗日乘子，之后各个EH 在新的拉格朗日乘子下继续进行更新，直至满足收敛条件。

基于ADMM 的EH 㶲损最小分布式优化的流程见附录A。

4 算例分析

4.1 算例设置

本文以同一能源配送网络下的3 个EH 为算例进行研究，通过MATLAB、YALMIP 和CPLEX 进行优化求解。每个EH 中均配备有CHP 系统与分布式光伏发电系统，其拓扑结构如图3 所示。

图3 多EH 拓扑结构Fig.3 Topological structure of multiple EHs

典型日EH 的电负荷及光伏出力如图4 所示，优化调度时间尺度取1 h，对典型日的各EH 调度进行优化。

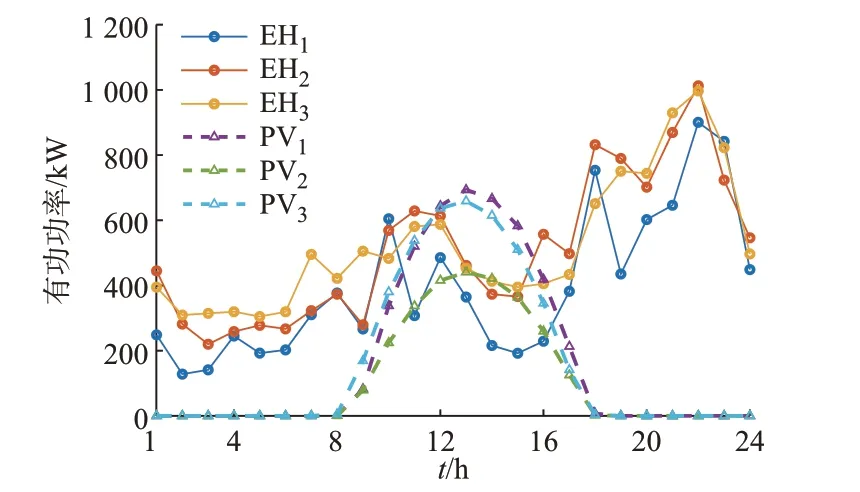
图4 典型日各EH 电负荷及光伏出力Fig.4 Electric load and photovoltaic output of different EHs in a typical day

各个EH 中CHP 机组参数如表1 所示。

EH 与电网间的联络线功率上限为1 000 kW，与热网间的联络线功率上限为1 500 kW。热力网络中，线路传输功率上限为2 000 kW，线路延迟系数为0.4，线路内工质流速为1 m/s，线路单位长度的损耗为20 kW/km，线路1、线路2、线路3 的长度分别为2、2、3 km，因此线路1、2、3 的延迟时间分别为0.8、0.8、1.2 h，热力损耗分别为40、40、60 kW。CHP 与热网通过换热器连接，其热效率为0.9，用户与热网直接连接。CHP 以热水形式输出热力，其供、回水温度分别为180 ℃和100 ℃，热网供、回水温度分别为90 ℃和70 ℃。EH 内用户的室内温度要求为20～25 ℃。天然气、煤、电力均为高品位能源，㶲折算系数取值为1，热力的㶲折算系数根据室内的温度上下限，经线性回归后求得为0.076 1，天然气低位热值为10.45（kW·h）/m3，电网煤折算系数为1.95。最大迭代次数取为500，最小迭代次数取为250，收敛精度取为0.05，惩罚系数为0.03。

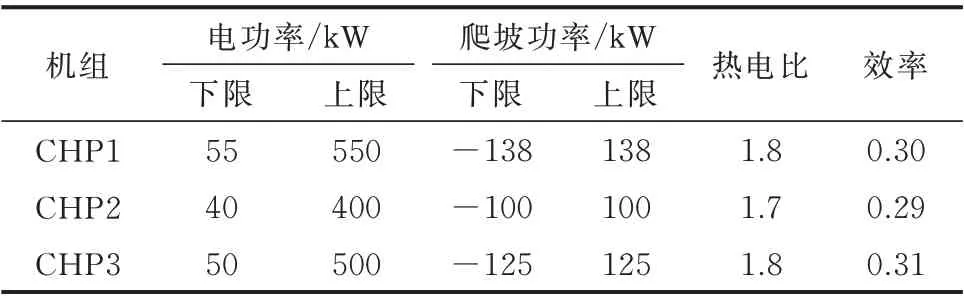
表1 CHP 机组参数Table 1 Parameters of CHP units

4.2 结果分析

4.2.1 优化调度结果分析

优化调度结果见附录B，其中图B1—图B3 为3 个EH 各自的CHP 电功率、与电网之间的购售电功率和相互之间的交互电功率。

由于EH 内部拥有大量的光伏设备，其运行在最大功率跟踪状态，当其处于出力高峰期时，EH 内部的电力负荷主要由光伏设备生产的电力进行供应，同时将过剩的电功率出售给电网。当光伏在夜间功率降低时，EH 内电力负荷主要由大电网和CHP 系统进行供应，由于不同CHP 系统的效率不同，效率较高的1 号和3 号CHP 系统发电功率较高，从而降低了整体系统的㶲损。CHP 系统受爬坡能力的限制，由于其在光伏高峰期时出力较低，因此在光伏出力低谷期无法立刻提供较大的功率支持。由于各个EH 之间可以进行电功率交互，相比于各自独立运行，整体系统的调度更为灵活，有利于降低系统㶲损。

附录B 图B4、图B5 和图B6 分别为各个EH 内的CHP 热功率、各用户的热功率和EH 与热力网络交互的热功率，图B7 为各个EH 内用户的室内温度曲线图，图B8 为热力网络内各个线路的首末端功率图。

在1～9 个优化周期内，CHP 出力较高，一方面由于室外温度较低，需要提供更多的热量以维持室内的温度，另一方面是光伏高峰期时，CHP 出力较低，从而导致维持室温较为困难，因此提前提供较高的热功率，使室内温度升高，利用室内较大的储热能力，从而在CHP 出力较低时期仍能维持室内所需的温度。在16：00 以后，CHP 逐渐恢复较高的输出功率，出于降低㶲损的考虑，仅将室内温度维持在所需温度的最低值。

由附录B 图B8 可知，各个热力线路由于热力传输延时的存在，因此其首末端功率并非实时相等。由于时段10～15 h 光伏出力较高，因此CHP 机组出力较低，导致热供应较少。因为热力管道的延时效应，热力管道传输功率开始缓慢下降，在时段15～20 h 达到最低值。由于热力管道延时的存在，一定程度上热力网络和CHP 在热力供应上形成了时间上的互补。同时，由于热力网络的存在，各个CHP 机组之间可以实现热力功率的交互，从而提升了整体的运行效率，降低了系统的㶲损。

下面针对系统中的㶲损分布进行分析，其中，㶲损主要发生在电网购电、CHP 系统、换热器、热网损耗以及用户采暖，其中电网购电的㶲损为标准煤㶲与电能㶲的差值，CHP 㶲损为输入的燃料㶲和输出的电能㶲和热量㶲的差值，热网损耗为供热管道上损失热量的㶲值，换热器和用户采暖㶲损为输入、输出热量㶲的差值，通过前文所建立的模型，求得的㶲损分布附录B 图B9 所示。图B9 可知，㶲损主要发生在CHP 系统将燃料转化为电力和热力的过程中，由于CHP 供能占比较高，且同等能量下燃料㶲与热量㶲的差值较大，所以CHP 部分的㶲损占了系统㶲损的大部分，其余部分的㶲损较为相近。

4.2.2 算法收敛性分析

由前文可知，各个EH 的㶲损函数及其约束条件均为线性模型，因此原优化模型为线性模型，其可以通过ADMM 进行有效的求解。通过转化为增广拉格朗日函数后，每个EH 优化模型的目标函数为二次函数，约束条件为线性函数，因此其为二次规划模型，则ADMM 整体的计算包括迭代次数乘EH 个数次二次规划的求解。

优化过程中残差最大值的迭代过程如附录B图B10 所示，各个等式约束的残差迭代过程如附录图B11—图B14 所示，㶲损迭代过程如图B15 所示。由以上各图可知，在最小迭代次数250 次以内，已经多次达到了残差精度要求，但由于未满足最小迭代次数，因此并未结束迭代，从而使得㶲损得以进一步下降，最终在347 次迭代时达到收敛条件。

优化运行所采用的硬件设备为Intel Core i7-8550U CPU @ 1.80 GHz、16 GB RAM，共耗时364.15 s，算例结果表明ADMM 可以有效解决多EH 联合运行的㶲损最小化分布式优化调度问题。

表2 给出了不同惩罚系数下的迭代次数、残差最大值以及目标函数值，最大迭代次数为500，最小迭代次数为250，收敛精度为0.05，保持不变。

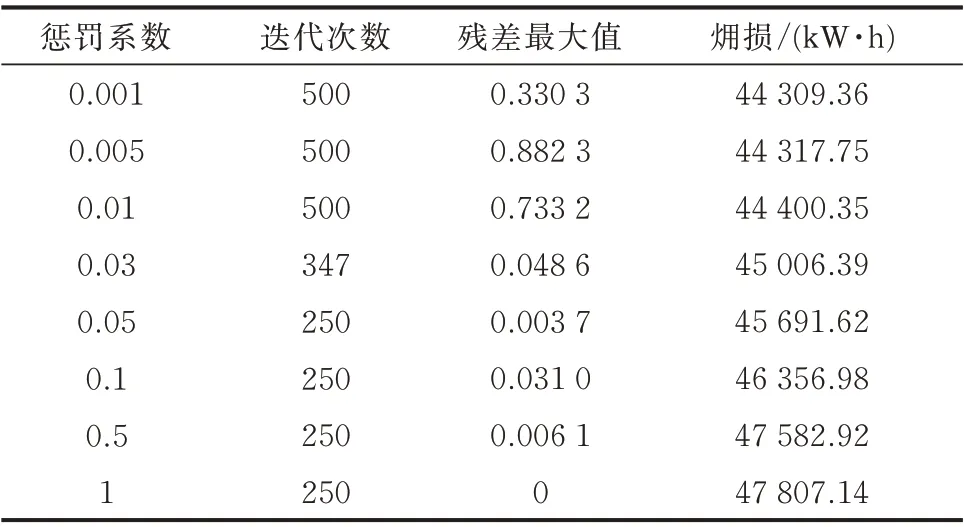
表2 不同惩罚系数对比Table 2 Comparison of different penalty coefficients

ADMM 在求解凸优化模型时，当其迭代次数趋近于无穷时，在理论上可以保证得到凸优化模型的最优解，但在实际应用中，由于迭代次数不可能趋近于无穷，因此其求得的最终解与最优解存在一定的偏差。而且ADMM 的收敛速度和最终解的数值均与惩罚系数相关，惩罚系数的适当选择较为重要，当其过小时，可以很快求得较低的㶲损，但残差往往难以满足精度要求，当其过大时，残差往往过快地达到了精度要求，从而导致了㶲损较大。可知，选择合适的惩罚系数，可以达到迭代次数较小、精度较高与㶲损较小之间的平衡，得到较好的优化效果。

4.2.3 分布式与集中式优化调度的比较分析

表3 给出了一天内各EH 在集中式优化调度和分布式优化调度2 种优化方式下各部分的㶲值。由于分布式优化采用迭代求解，当误差小于给定值时迭代收敛。因而，最终的结果与集中式优化难以保证完全一致。通过对比可以看出，2 种优化调度方式下㶲损的差别很小，分布式优化仅比集中式优化高1.57%左右，其对优化结果的影响可以忽略。

表3 集中式优化与分布式优化结果对比Table 3 Comparison of centralized optimization and distributed optimization results

4.2.4 㶲损最小与成本最小优化调度比较分析

本文设置了以下成本最小的优化调度模型与前文的㶲损最小的优化调度模型进行对比分析。成本最小优化模型的目标函数如下：

约束条件与前文优化模型相同。

㶲损最小与成本最小的优化结果如附录B 图B16—图B18 所示。与以㶲损最小化为目标相比，以成本最小为目标时，CHP 机组的出力在时段1～8 h 内较小，而在时段16～22 h 内出力较大，这是因为在时段1～8 h 内，电网售电价格较低，因此以成本最小为目标时倾向于在电网中购买更多的电力；在时段16～22 h 内电网售电价格较高，因此倾向于增加CHP 机组的出力。而对于以㶲损最小为目标时，虽然CHP 机组热效率很高，但由于大部分为热力功率，其㶲效率较低，所以一般使其运行在满足热负荷的最低状态，不足的电力由电网供应。因此，在以成本最低为目标时，为了在电力价格高峰期降低成本，提高CHP 机组电力出力的同时也提高了热力出力，使得用户室内的温度在时段17～24 h 内有所提高。

㶲损最小化与成本最小化的优化结果对比如表4 和表5 所示。