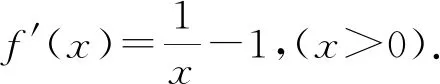一道高考导数题的思考与探索*
2021-05-07陈炳泉
陈炳泉
(福建省仙游县华侨中学 351200)
函数与导数及其应用在高中数学的学习中占有举足轻重的地位,并且与其他知识点融合性强,近几年的高考中,对函数与导数及其应用的考题屡见不鲜且常考常新,较为全面地考查了数学学科核心素养.
含参数的不等式恒成立,求解参数范围,解题的一个基本方法是以函数的视角来考虑与解决问题,本质上是将其转化为函数最值或函数值大小比较的问题.本文以2020年新高考I卷(山东卷)数学第21题为载体,探讨含参不等式恒成立问题中参数范围的常见解题策略.
1 试题再现
(2020新高考Ⅰ卷(山东卷)数学第21题)已知函数f(x)=aex-1-lnx+lna,
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;(解略).
(2)若f(x)≥1,求a的取值范围.
1.1 常见解法
本题是考查函数与导数的应用,涉及到与函数相关的不等式证明问题、利用导数研究函数的单调性、极值,函数的零点等问题.着重体现了对数学学科中逻辑推理以及数学运算核心素养的考查.此类问题解法灵活多样,如,必要性探路法、分离参数法、含参分类讨论法等等.
解法1:必要性探路法
必要性:由题可知,必有f(1)=a+lna≥1.因为g(x)=x+lnx在(0,+∞)上单调递增,且g(1)=1,所以a≥1.
充分性:当a≥1时,
f(x)=aex-1-lnx+lna
≥ex-1·1-lnx+ln1=ex-1-lnx.
又因为ex-1≥(x-1)+1=x,
-lnx≥-(x-1)=-x+1.
当x=1时,上述两个不等式同时取等号(证明略),
所以ex-1-lnx≥1.
综上所述,a的取值范围是[1,+∞).
解法2:分离参数法
f(x)=aex-1-lnx+lna
=elna+x-1-lnx+lna,
要使f(x)≥1也即elna+x-1-lnx+lna≥1,
即elna+x-1+lna-1≥lnx,
即elna+x-1+lna+x-1≥lnx+x=elnx+lnx.
令g(t)=et+t,(t∈R)故只需
g(lna+x-1)≥g(lnx)即可.
因为g(t)是增函数,
所以只需lna+x-1≥lnx.
故f(x)≥1⟺lna≥lnx-x+1.
令h(x)=lnx-x+1(x>0),
则只需lna≥[h(x)]max.

x∈(1,+∞)时,h′(x)<0.
所以h(x)在(0,1)上递增,在(1,+∞)上递减.
则有h(x)max=h(1)=0.故lna≥0所以a≥1.
即a的取值范围是[1,+∞).
解法3:含参分类讨论
因为f(x)=aex-1-lnx+lna,
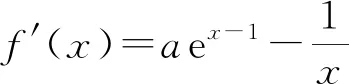
易知y=f′(x)在(0,+∞)上单调递增.
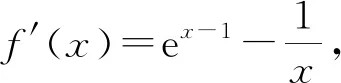
则f′(1)=0.
所以,x∈(0,1)时f′(x)<0,f(x)单调递减;
x∈(1,+∞)时,f′(x)>0,f(x)单调递增.
fmin(x)=f(1)=e0-ln1=1,
所以f(x)≥1成立.
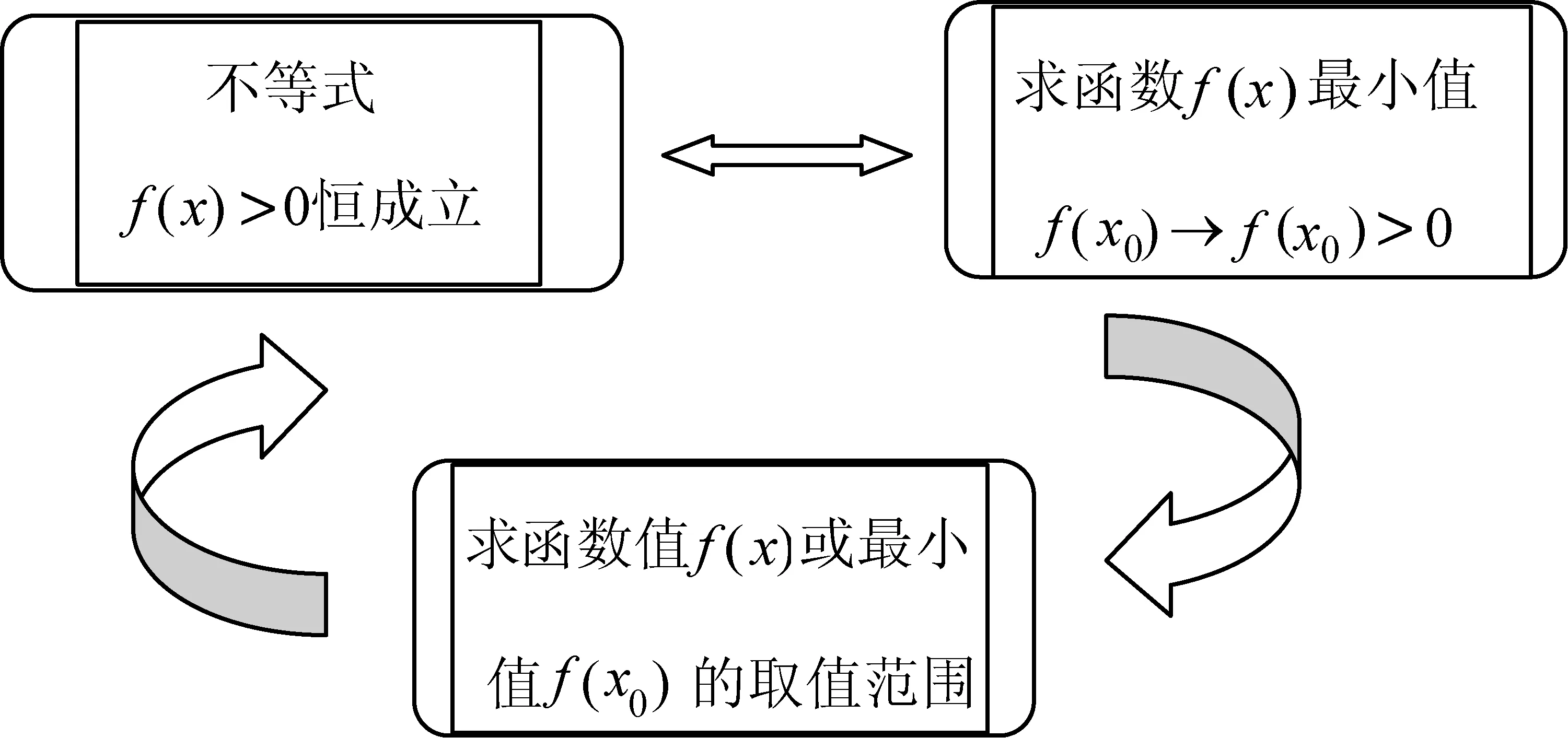
②0 ③a>1时,aex-1-lnx+lna>ex-1-lnx≥x-lnx≥1,故f(x)≥1成立. 综上所述,a的取值范围是[1,+∞). 上述的三种解题过程都蕴含了丰富的数学思想并体现了对逻辑推理及数学运算核心素养的要求.解法1运用了必要性探路法,看似解题过程简单,实际上找到合适的切入点需要强大的数学基础和逻辑推理做支撑,如何确定取值,是一个难点. 分离参数法是解决含参不等式恒成立求参数问题中常用的解法,即将不等式中的参数与未知数进行分离,使之化简为a≥g(x)(或a≤g(x)),则有:(1)a≥g(x)恒成立⟺a≥gmax(x);(2)a≤g(x)恒成立⟺a≤gmin(x).但是,对于本题指数式与对数式混合的结构,并不宜直接分离参数a.故而我们尝试通过指数式与对数式之间恒等变换,构造新的函数式不等关系,使得原不等式得以化简,进而分离参数a.如解法2中,利用指数式的变形aex-1=elna+x-1,x=elnx,将原命题中f(x)≥1恒等变换为不等式elna+x-1+lna+x-1≥elnx+lnx.令g(t)=et+t,则f(x)≥1⟺g(lna+x-1)≥g(lnx)⟺lna+x-1≥lnx.如此,原命题中含有指数式与对数式混合结构的不等式便得以简化,转化为只含有对数式结构的不等式恒成立问题.此时,我们便可分离出参数lna,令h(x)=lnx-x+1,则lna+x-1≥lnx恒成立⟺lna≥[h(x)]max,可先求出lna范围,再求得参数a的范围.显然,分离参数法在本题中的运用必须对原不等式进行一番改头换面,才得以成行,其中不仅需要数学运算功底扎实,更需要原不等式的结构设计得巧妙.由此可见,分离参数法在复杂的不等式结构中,也许并不易,且不宜.对于大多数结构较为复杂的含参不等式而言,解法3的含参分类讨论更加具有普遍适用性,是“通性通法”. 策略一:放缩法证明不等式成立 详解见本例解法3: 当a>1时,aex-1-lnx+lna>ex-1-lnx≥x-lnx≥1,故f(x)≥1成立. 策略分析:既然转化为函数不好求解,不妨考虑直接证明不等式恒成立.这里面运用了两个不等式:(1)ex≥x+1;(2)x≥1+lnx对原不等式进行放缩,大大地简化了原不等式的结构,快速地证明了a>1时,f(x)≥1恒成立.利用放缩法证明不等式,直接跨越了导函数求零点的过程,其便捷性不言而喻;但与其同时,我们也得意识到,这种放缩法并非“放之四海而皆准”的,它对缩放的精准程度是有要求的. 策略二:设而不求,代换隐零点 因为f(x)=aex-1-lnx+lna, 易知y=f′(x)在(0,+∞)上单调递增. 则f′(1)=0. 所以,x∈(0,1)时f′(x)<0,f(x)单调递减; x∈(1,+∞)时,f′(x)>0,f(x)单调递增. fmin(x)=f(1)=e0-ln1=1, 所以f(x)≥1成立. ②0 且当x∈(0,x0)时,f′(x)<0,f(x)单调递减; x∈(x0,+∞)时,f′(x)>0,f(x)单调递增. 所以fmin(x)=f(x0)=aex0-1-lnx0+lna 故fmin(x)>1,f(x)≥1恒成立. 综上所述,a的取值范围为[1,+∞). 策略三:设而不求,隐零点反解求参数 因为f(x)=aex-1-lnx+lna, 易知y=f′(x)在(0,+∞)上单调递增. 则f′(1)=0. 所以,x∈(0,1)时f′(x)<0,f(x)单调递减; x∈(1,+∞)时,f′(x)>0,f(x)单调递增. fmin(x)=f(1)=e0-ln1=1, 所以f(x)≥1成立. ②0 当x∈(0,x0)时,f′(x)<0,f(x)单调递减; x∈(x0,+∞)时,f′(x)>0,f(x)单调递增. (i) 故fmin(x)=f(x0)=aex0-1-lnx0+lna (ii) 易知y=g(x)在(0,+∞)上是减函数, 且g(1)=1.故当x∈(0,1]时,g(x)≥1. 因为f(x)≥1恒成立⟺fmin(x)≥1⟺f(x0)≥1, 所以x0∈(0,1]. (iii) 当x∈(0,1]时,a′(x)<0, 故函数y=a(x)在(0,1]上是减函数. 故a>1时不等式成立. 综上所述,a的取值范围为[1,+∞). 含参分类讨论中参数范围的求解,利用导数研究函数单调性,得到导函数的零点x0(解方程f′(x0)=0),进而得函数最值f(x0),由f(x0)≥1解得参数范围是一种基本方法.但在不便直接求解方程f′(x0)=0的根(即求导函数零点x0)的时候,该如何化解这个问题呢?我们探索了两种途径来解决这个问题:其一,以不等式的角度来进行证明,可利用不等式的性质,运用放缩法证明不等式恒成立(策略一);也可从函数的角度来看待这个问题,通过函数最值f(x0)的取值范围来证明不等式恒成立(策略二).其二,利用参数a与导函数零点x0的关系f′(x0)=0→a=φ(x0),由f(x)≥1求得零点x0的取值范围,再利用函数关系a=φ(x0)反解得到参数a的取值范围. 上述的策略一与策略二都运用了数学化归转化思想,将函数最值的求值转化为不等式证明或函数最值的取值范围.这其中蕴含着数学“等量关系”与“不等关系”两者的联系与转化,需要我们在平时的数学学习中对知识间的联系进行思考并总结规律,我们也可以从课本中的题目中找到启发. 如,高中数学人教A版教科书,选修2-2,第32页,习题1.3 B组第1题: 利用函数的单调性,证明下列不等式,并通过函数图象直观验证: (1)sinx (2)x-x2>0,x∈(0,1); (3)ex>1+x,x≠0; (4)lnx 本题中的(3),(4)两小题也即我们在策略一:使用放缩法证明不等式过程中运用到的结论.证明如下: (3)设f(x)=ex-1-x,x≠0, 因为f′(x)=ex-1,x≠0, 所以,当x>0时,f′(x)>0,f(x)在(0,+∞) 上单调递增;当x<0时,f′(x)<0,f(x)在(-∞,0)上单调递减. 故x≠0时,总是有f(x)>f(0)=0, 即ex-1-x>0. 所以x≠0时,ex>1+x. (4)设f(x)=lnx-x,x>0, 当0 故,当x>0时,总是有 f(x)≤fmax(x)=f(1)=-1, 即lnx-x≤-1. 所以,x>0时,lnx≤x-1 由(3)可知,x>0时,ex>1+x>x. 综上,当x>0时,lnx 习题(3),(4)中,以不等式的角度直接去证明f(x)>0成立是不适宜的,在f(x)>0这个不等关系中,我们会联想到比较特殊的一个临界值,即函数f(x)的最值f(x0).通常,我们可利用函数最值,实现不等关系与等量关系的一个转化: 不等式f(x)>0恒成立⟺函数f(x)的最小值f(x0)>0. 如题(4)中,就是通过函数最值的求解,结合不等式性质,证明了x>0时,lnx 但是在题(3)中,x≠0时,f(x)=ex-1-x的最小值是不存在的,此时我们再次转换角度,不求函数最值,转而通过函数值f(x)的取值范围来证明不等式f(x)>0恒成立.这种思考方向非常值得我们借鉴和运用.在函数f(x)的最值无法求解,或是不易求解时,我们可以尝试能否通过函数值f(x)的取值范围,或是函数f(x)最小值f(x0)的取值范围来证明不等式.(如图所示). 即等量关系与不等关系的转化: 正如我们遇到本文高考题中,函数最值f(x0)求而不得时,可尝试逆向思维:函数最值(f(x0)的值)→函数最值范围(f(x0)≥1)→不等式成立(f(x)≥1). 一道典型的问题可以引导启发学生思维上的多角度思考与拓展.通过上述不同的解题途径,我们可以领略到函数、导数与其他知识的综合交融及其灵活多变,虽然解题方法不同,但其核心思想始终围绕着函数.在解题过程中,无论是不等式的放缩法应用,函数隐零点的设而不求,整体代换亦或是反解求参数,都蕴含着数学转化与化归思想的应用,体现了对逻辑推理与数学运算学科核心素养的要求.对于含参不等式恒成立中参数范围的求解问题,含参分类讨论法更加通用,适用范围更广,它的解题步骤朴素却不简单,需要具备清晰的数学逻辑思维和扎实的数学运算功底. “不积跬步,无以至千里;不积小流,无以成江海.”在平时的学习中,我们应重视对数学必备知识与关键能力的深度理解,多方位多角度去思考问题,构建知识间的联系与转化,由特殊到一般地寻找规律,探索解题的通性、通法,提升数学学科核心素养.1.2 解后反思
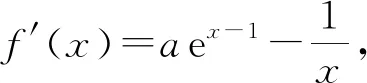
2 含参分类讨论中隐零点的化解策略探索
2.1 隐零点化解策略
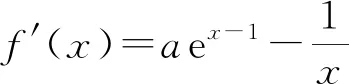
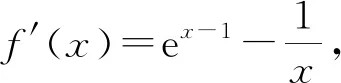
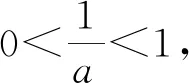

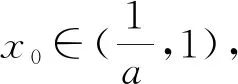

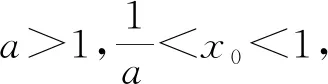

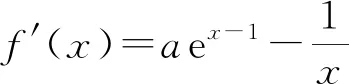
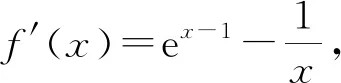
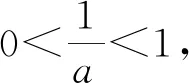

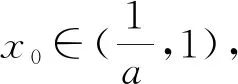

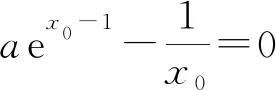
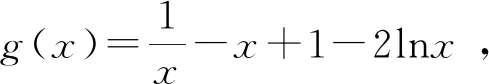



2.2 解后反思