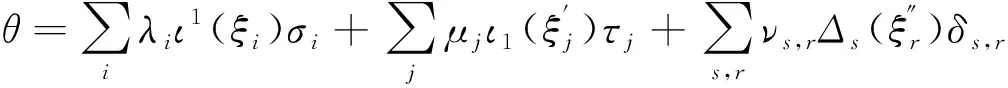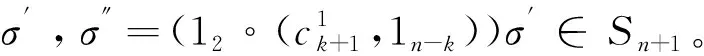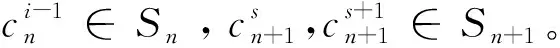结合代数Operad的截面理想
2021-05-07魏思凡王之梁赵志兵
魏思凡,王之梁,赵志兵
(安徽大学 数学科学学院,合肥 230601)
0 引 言
Operad理论最早出现于20世纪60年代Boardman-Vogt[1]和May[2]关于代数拓扑学的著作中。此后,Operad理论被广泛地用于代数学,组合学,几何学和拓扑学等多个领域[3-4]。文中引入了2-酉Operad的定义,尤其是结合代数Operad-Ass,并给出这类Operad的基定理,便于通过截面理想研究其增长性质。
PI代数是非交换领域中重要的代数类,它与多项式代数有着许多类似的同调性质。注意到PI-代数类与结合代数Operad Ass的非零理想一一对应,即结合代数A是PI-代数等价于A是Ass/I上的代数,其中I为Ass的某个非零理想[5-7],而Ass的理想又等价于T-理想[8-9]。因此,结合代数Operad理想结构,尤其是理想的生成元的研究,对于PI-代数的研究有着重要意义。另一方面,Bao等在文献[10]中证明了结合代数Operad的任一理想都位于两个截面理想之间,因此截面理想的结构对于Ass的理想研究也有着十分重要的价值。本文主要通过引入Ass的一些线性算子,利用基定理和数学归纳法证明第k个截面理想kΥ可由kΥ(k+2) 或kΥ(k+1)Uk+1Υ(k+2)生成。
1 预备知识
首先回顾一些基本定义。设K是特征为零的域。
定义1[11]设P={P(n)}n≥0是N-分次K-向量空间,1∈P(1) ,且对整数 k1,…,kn≥0,有P上的复合映射
∘:P(n)×P(k1)×…×P(kn)→P(k1+…+kn)
(θ,θ1,…,θn)θ∘(θ1,…,θn)
满足下面两条公理:
(1) 对任意θ∈P(n), 有θ∘(1,1,…,1)=θ=1∘θ,
(2) 对任意θ∈P(n),θi∈P(ki),θij∈P(lij),n>0,ki≥0,lij≥0,j=1,…,kj,i=1,…,n,有
θ∘(θ1∘(θ1,1,…,θ1,k1),…,θn∘(θn,1,…,θn,kn))=
θ∘(θ1,…,θn)∘(θ1,1,…,θ1,k1,…,θn,1,…,θn,kn)
若ki=0,则约定θi∘()=θi。则称P为非对称Operad。
为叙述方便起见,我们将n阶置换σ∈Sn记为σ=(i1,i2,…,in),其中ik=σ-1(k),k≥1。
例1 设Ass(n)=KSn是以n阶对称群Sn中的元素为基生成的自由向量空间,n=0,1,…。 则Ass={Ass(n)}n≥0构成非对称Operad,其复合映射定义如下:
∘:Sn×Sk1×…×Skn→Sk1+…+kn
(σ,σ1,…,σn)σ∘(σ1,…,σn)
其中:σ∈Sn,σi∈Ski,1≤i≤n。σ∘(σ1,…,σn)的运算规则如下:

记S为所有n阶对称群{Sn}n≥0的不交并。称
M={M(0),M(1),…,M(n),…}
为右KS-模,其中每个M(n)为右KSn-模,n≥0。
定义2[11-12]设P是非对称Operad,若P={P(n)}n≥0是KSn-模且P上的复合映射满足
(θ*σ)∘(θ1*σ1,…,θn*σn)=(θ∘(θσ-1(1),…,θσ-1(n)))*(σ∘(σ1,…,σn)),
其中:θ∈p(n),θi∈p(ki),σ∈Sn,σi∈Ski,n>0,ki≥0,i=1,…,n。记*为右Sn作用,σ∘(σ1,…,σn)是Ass中的复合映射,则称P为对称Operad,简称Operad。
定义3[11]设P={P(n)}n≥0是Operad,11为P(n)的单位。
(1) 若P(0)=K10≅K,则称P为酉Operad,10是P(0)的基。
(2) 设P是酉Operad,若存在12∈P(2),对任意θ∈P(n)有
12∘(θ,10)=θ=12∘(10,θ)
则称P为2-酉Operad,12为2-单位。
(3) 若P是2-酉Operad,对任意正整数n≥3,归纳定义
1n=12∘(1n-1,11),1′n=12∘(11,1′n-1)
若1n=1′n,则称1n为n-单位。记P为2a-酉Operad。显然地,Ass是2a-酉operad。
定义4 记集合[n]:={1,2,…,n}。设P是酉Operad,θ∈P(n),其单位记为11。对I⊆[n],称映射
πI:P(n)→P(s)
πI(θ)=θ∘(1χI(1),…,1χI(n))

ΓI:P(n)→P(n-s)
称映射
ΔI:P(n)→P(n+s)
ΔI(θ)=θ∘(1χI(1)+1,…,1χI(n)+1)
为扩张算子[13]。设l,r为非负整数,称映射
为增量算子。其中s=|I|为I中的元素个数,χI是I的特征函数。
命题1[10]设P是2-酉Operad,θ∈P(n),则

(2) Γi1,…,is=Γis-s+1·…·Γi2-1·Γi1=Γi1·…·Γis,其中{i1,…,is}⊆[n]且i1<… (3)θ∘(1k1,…,1kn)=((Δ1)k1-1·…·(Δn)kn-1)(θ),其中n,k1,…,kn=0,1,…。 定义5[11]设I是P的S-子模。对任意的整数n>0,k1,…,kn≥0,若 I(n)∘(P(k1),…,P(kn))⊆I(k1+…+kn) P(n)∘(P(k1),…P(ks-1),I(ks),P(ks+1),…,P(kn))⊆I(k1+…+kn) 则称I是P的理想,P/I为P的商Operad。 定义6[10]设P是酉Operad,k,n为非负整数。记kΥ={kΥ(n)}n≥0为P的KS-子模,其中 约定0ΥP=P。易证kΥP是P的理想,称kΥP为P的第k个截面理想。一般记kΥP为kΥ。 设I={i1,…,is}⊆[n],i1<… 命题2[10]设P是2-酉Operad,kΥ(n)为P的截面理想,n,k为整数且n≥k≥0。令kΥ(k)的基为Bk={θi|1≤i≤fP(k)},其中fP(k)=dimkΥ(k),则 {12∘(θi,1n-k)*cI|1≤i≤fP(k),I⊆[n],|I|=n-k} 为(kΥ/k+1Υ)(n)的基。 设X为P的子集,记〈X〉为X生成的理想。若存在P的有限维子空间X,使P中的每个元素均可由X中的元素通过复合映射和Sn作用生成,则P是有限生成的。 生成的KSn模。 令Φ2=12-τ,其中12是S2中的恒等置换,τ=(2,1)是S2中的对换。 命题4[10]设kΥ是Ass的截面理想,则1Υ=2Υ=〈Φ2〉。 命题5[10]设kΥ是Ass的截面理想,n,k均为整数且n≥k≥1。那么当且仅当θ∈kΥ(n),有Φ2∘(11,θ)∈k+1Υ(n+1), 12∘(θ,Φ2)∈k+2Υ(n+2)。 在证明主要结论之前,先引入以下几条引理。 引理1 设整数n≥1,则对任意的θ∈Ass(n),τ∈Sn有 Rs(θτ)=Rτ(s)(θ)τ,Σs(θτ)=Στ(s)(θ)τ。 引理2 设kΥ是Ass的截面理想,整数n≥k>0,s∈[n]。则对任意的θ∈kΥ(n)有 Rs(θ)∈kΥ(n),Σs(θ)∈kΥ(n)。 证明设任意的I⊆[n-1],|I|=k-1。由θ∈kΥ(n),可知πI(Γs(θ))=0。故Γs(θ)∈kΥ(n-1)。同理,ι1(Γs(θ))∈kΥ(n)。因为kΥ(n)是Ass的理想,所以 Rs(θ)=ι1(Γs(θ))cs∈kΥ(n),Σs(θ)=θ-Rs(θ)∈kΥ(n)。 对任意i∈[n],当s=i时,有 Γs(Rs(θ))=Γs(ι1(Γs(θ))cs)= 即Γs(Σs(θ))=0。若s≠i,设Γi(θ)=0。一方面,当i>s时, Γi(Rs(θ))=Γi(ι1(Γs(θ))cs)= 另一方面,当i Γi(Rs(θ))=Γi(ι1(Γs(θ))cs)= 0=Γs(Rs-1(Σs·Σs+1·…·Σn)(θ))= Γs((Σs·Σs+1·…·Σn)(θ))-Γs((Σs-1·Σs·…·Σn)(θ))= -Γs((Σs-1·Σs·…·Σn)(θ)) 且对任意s∈[n],有Γs((Σs+1·…·Σn)(θ))∈kΥ(n-1),所以 Rs((Σs+1·…·Σn)(θ))=ι1(Γs(Σs+1·…·Σn(θ)))cs∈〈kΥ(n-1)〉(n) 引理4 设kΥ是Ass的截面理想,k,m,n为整数且n≥k≥0,m≥1。则对任意θ∈kΥ(n),φ∈1Υ(m),有 12∘(θ,φ)∈〈k+2Υ(n+2)〉(n+m) 证明由截面理想的定义知 则1Υ(m)可由{1m-σ|σ∈Sm,σ≠1m}生成。另外,对σ1,…,σs∈Sm,1≤s≤m!,有 1m-σ1…σs=(1m-σs)+(σs-σs-1σs)+…+(σ2…σs-σ1…σs)= (1m-σs)+(1m-σs-1)σs+…+(1m-σ1)σ2…σs。 由于{(12),(23),…,(m-1,m)}是Sm的生成元集,其中(i,i+1)是Sm中的对换,1≤i≤m-1,故1Υ(m)是由1m-(12),1m-(23),…,1m-(m-1,m)生成的右Sm-模。因而只需考虑φ=1-(i,i+1)的情况。因为 12∘(θ,1-(i,i+1))= 12∘(θ,1-(1,2…i))-12∘(θ,(i,i+1)-(12…i))= ιm-i((Δn+1)i-2(12∘(θ,Φ2)))-ιm-i-1(((Δn+1)i-1(12∘(θ,Φ2)))(i,i+1)) 且12∘(θ,Φ2)∈k+2Υ(n+2),所以 12∘(θ,1-(i,i+1))∈〈k+2Υ(n+2)〉(m+n) 引理5 设kΥ是Ass的截面理想,s,k,r为非负整数且1≤s≤k+r。令θ∈kΥ(k),σ∈Sk+r,则 (1) 当σ(s)≤k时, Σs(ιr(θ)σ)=ιr(θ)σ; (2) 当σ(s)>k时, Σs(ιr(θ)σ)∈〈k+2Υ(k+2)〉(k+r); (3) (Σ1·…·Σk+r)(ιr(θ)σ)∈〈k+2Υ(k+2)〉(k+r)。 证明(1) 若σ(s)≤k,则Γσ(s)(ιr(θ))=0,从而Rσ(s)(ιr(θ))σ=0,故 Σs(ιr(θ)σ)=ιr(θ)σ (2) 由引理1知只需证明σ=1k+r的情况。当σ=1k+r时,σ(s)=s。因为 (3) 令s为使σ(s)>k的最大整数,由(1)和(2)知 (Σs·…·Σk+r)(ιr(θ)σ)∈〈k+1Υ(k+2)〉(k+r) 从而有(Σ1·…·Σk+r)(ιr(θ)σ)∈〈k+2Υ(k+2)〉(k+r)。 定理1 设kΥ是Ass的截面理想,k为整数且k≥1,则kΥ=〈kΥ(k+2)〉。特别地,kΥ是有限生成的。 证明对k用归纳法。当k=1时,由命题4知 1Υ=〈Φ2〉=〈1Υ(2)〉=〈1Υ(3)〉 设k-1Υ=〈k-1Υ(k+1)〉,下证kΥ=〈kΥ(k+2)〉,即证对任意n≥k,有kΥ(n)=〈kΥ(k+2)〉(n)。 对n用归纳法。当n=k,k+1时,有kΥ(k)=〈kΥ(k+2)〉(k),kΥ(k+1)=〈kΥ(k+2)〉(k+1)。令n≥k+1,假设对任意的整数m,当k≤m≤n时,有kΥ(m)=〈kΥ(k+2)〉(m)。下面证明kΥ(n+1)=〈kΥ(k+2)〉(n+1)。由于Ass的截面理想是降链[6],故对任意θ∈kΥ(n+1),有 θ∈kΥ(n+1)⊆k-1Υ(n+1)=〈k-1Υ(k+1)〉(n+1) 根据命题3知 θ-(Σ1·…·Σn+1)(θ)∈〈kΥ(n)〉(n+1)⊂〈kΥ(k+2)〉(n+1) 因而只需证明(Σ1·…·Σn+1)(θ)∈〈kΥ(k+2)〉(n+1)。结合θ的分解式,只需证明 (1) (Σ1·…·Σn+1)(ι1(ξ)σ)∈〈kΥ(k+2)〉(n+1), (2) (Σ1·…·Σn+1)(ι1(ξ)σ)∈〈kΥ(k+2)〉(n+1), (3) (Σ1·…·Σn+1)(Δs(ξ)σ)∈〈kΥ(k+2)〉(n+1)。 其中:ξ∈kΥ(n),σ∈Sn+1,s∈[n]。 对任意n≥k+1,由命题2知(kΥ/k+1Υ)(n)的基为 {ιn-k(ξi)cI|ξi∈Bk,I⊆[n],|I|=n-k} 其中:Bk={ξi|1≤i≤fP(k)}是kΥ(k)的基,fP(k)=dimkΥ(k)。则对任意的ξ∈kΥ(n),存在ξ′∈k+1Υ(n),使得 其中:ξi∈Bk,Ii⊆[n],|Ii|=n-k。由归纳假设知 ξ′∈k+1Υ(n)⊆kΥ(n)=〈kΥ(k+2)〉(n) 则ι1(ξ′)σ,ι1(ξ′)σ,Δs(ξ′)σ∈〈kΥ(k+2)〉(n+1),其中σ∈Sn+1,s∈[n], 令ξ=ιn-k(φ)cI,其中φ∈kΥ(k),I⊆[n],|I|=n-k。下面证明对ξ=ιn-k(φ)cI有(1),(2), (3)成立。 (1) 因为ι1(ξ)σ=ι1(ιn-k(φ)cI)σ=ιn-k+1(φ)σ′,所以由引理5 (3)得 (Σ1·…·Σn+1)(ι1(ξ)σ)=(Σ1·…·Σn+1)(ιn-k+1(φ)σ′)∈〈k+2Υ(k+2)〉(n+1)⊂〈kΥ(k+2)〉(n+1), 其中σ′=(12∘(cI,11))σ∈Sn+1。 (2) 因为ι1(ξ)σ=(ιn-k(ι1(φ)))σ′,所以由命题5知 Φ2∘(11,φ)∈k+1Υ(k+1)⊆kΥ(k+1)=〈kΥ(k+2)〉(k+1), 其中:σ′=(12∘(11,cI))σ∈Sn+1。因此ιn-k(Φ2∘(11,φ))σ′∈〈kΥ(k+2)〉(n+1)。自然地, (Σ1·…·Σn+1)(ιn-k(Φ2∘(11,φ))σ′)∈〈kΥ(k+2)〉(n+1) (Σ1·…·Σn+1)(ι1(ξ)σ)=(Σ1·…·Σn+1)(ιn-k(ι1(φ))σ′)∈〈kΥ(k+2)〉(n+1)。 Sn+1,s′=cI-1(s)∈[n]。由s的任意性,记s′=s。因为 所以只需考虑1≤s≤k的情况。由于对任意i∈[n],有 Σi(Δs(ιn-k(φ)))∈〈k+2Υ(k+2)〉(n+1)⊂〈kΥ(k+2)〉(n+1)。 对任意的σ∈Sn+1,设r为使σ(r)>k+1的最大整数,有 (Σr·…·Σn+1)((Δs(ιn-k(φ)))σ)∈〈kΥ(k+2)〉(n+1), 故(Σ1·…·Σn+1)((Δs(ιn-k(φ)))σ)∈〈kΥ(k+2)〉(n+1)。 综上,kΥ(n+1)⊆〈kΥ(k+2)〉(n+1)。另外,反包含的证明是容易的,故kΥ=〈kΥ(k+2)〉。 因为kΥ(n)作为向量空间是有限维的,所以kΥ是有限生成的。 定理2 设kΥ是Ass的截面理想,则kΥ由kΥ(k+1)和k+1Υ(k+2)生成。 证明这是引理3和定理1的直接结果。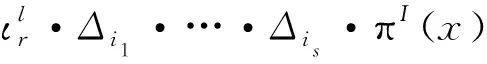






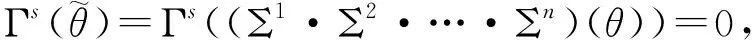
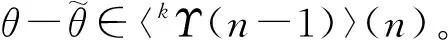
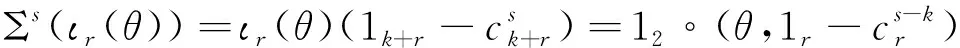
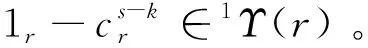
2 主要结果