分段插值函数在电解质溶解度的应用

姚 星 刘炳廷 杨志高 罗一澳 廖芳芳

（湘南学院数学与金融学院 湖南·郴州 423000）

0 引言

固体溶解度数据是研究工业结晶分离过程、探讨传质机理及化工设计和开发的重要基础物性数据。然而，溶解度数据主要是在实验室中测出结果，但是从实验得到数据的所有结果也是非常困难的事。如果能通过实验测定一部分数据之后，再通过数值计算近似得到其余部分的数据，那么会在很大程度上减少资源和人力的浪费。比如电解质氯化镁在0℃下的溶解度为52.9；10℃下的溶解度为53.6；20℃时的溶解度为54.6……，但是如果你想得到15℃时的溶解度值是多少时，就可以根据它在其他温度下的溶解度通过数值方法和数值计算来得到，不用再次通过实验测定得到，从而可以减少不必要的资源浪费和实验过程。

生活中，有许多固体电解质都被我们利用到，例如我们的药物。药物是我们生活的必需品，而药物的溶解度会影响药物的生物活性，近年来出现了很多新药物，但新药的溶解度数据测量却比较繁琐。这时，我们可以通过测定一些温度下的溶解度然后近似计算出其他温度下的溶解度，此时，我们可以采用各种方法来计算。

本文运用分段线性插值和三次样条插值，研究了九种电解质在30℃下的溶解度，并进一步通过曲线拟合与已有结果进行比较。

1 电解质和溶解度的定义

1.1 电解质

电解质是溶于水溶液中或在熔融状态下能够导电的化合物，大都是以离子键或极性共价键结合的物质。

1.2 溶解度

溶解度：在一定温度下，某固态物质在100g溶剂（通常为水）中达到饱和状态（溶解溶剂的最大量）时所溶解的溶质的质量。

2 九种电解质在不同温度下的溶解度

通过查找化学手册，得到表1中不同电解质在不同温度下的溶解度。

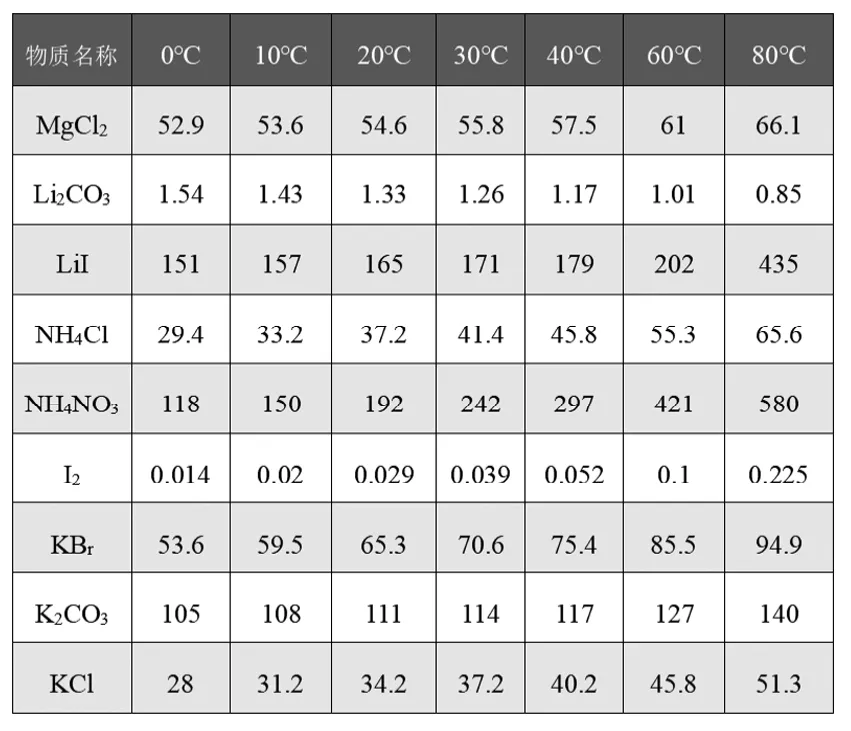
表1：常见九种电解质在不同温度下的溶解度(g/100g水)

3 分段线性插值计算溶解度

以温度为自变量，对应的溶解度为因变量，运用分段线性插值函数，以 0，10，20，40，60，80 为节点在Matlab软件进行编程，计算在插值点30℃时的溶解度。

Matlab程序如下：

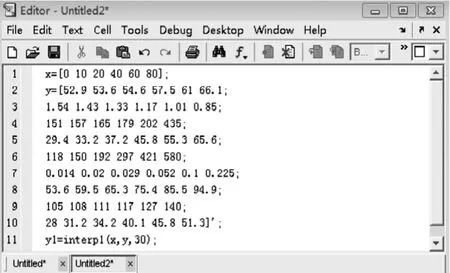
图1：分段线性插值法在30℃时的溶解度的求解程序

程序结果：

图2：分段线性插值法在30℃时的溶解度

4 三次样条插值计算溶解度

以温度为自变量，对应的溶解度为因变量，运用三次样条插值函数，以 0，10，20，40，60，80 为节点在Matlab软件进行编程，计算在插值点30℃时的溶解度。

程序如下：（见图 3）。

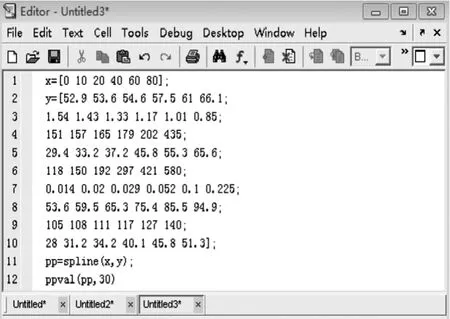
图3：三次样条插值法在30℃时的溶解度的程序求解

结果如下：（见图 4）。

图4：三次样条插值法在30℃时的溶解度

5 分段线性插值与三次样条插值在30℃电解质溶解度的比较

5.1 相对误差

从表2中我们可以看出一些电解质在用分段线性插值所得的误差比较小，而有的电解质用三次样条插值所得的结果更为精确。

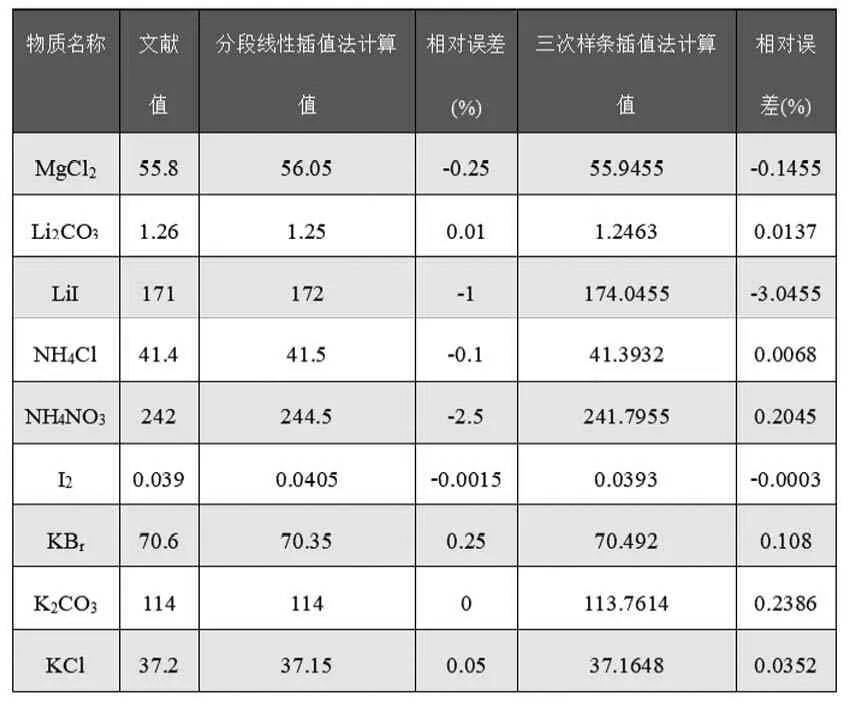
表2：相对误差

5.2 曲线拟合

曲线拟合：根据一组平面上的点，要求确定一个函数y=f（x），即曲线，使得这些点尽量与曲线接近，这就是曲线拟合。从而可以设拟合多项式为：

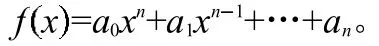
用Matlab编程来计算分别用分段线性插值和三次样条插值的方法得到的拟合多项式。

代码如下：（见图 5）。

图5：一元拟合多项式求解程序

y1表示了表格中的九种电解质在30℃时溶解度的文献值，y2表示了表格中的九种电解质用分段线性插值法计算出在30℃时溶解度的值，y3表示了表格中的九种电解质用三次样条插值法计算出在30℃时溶解度的值。

pk1是利用分段线性插值法的原理得到的一元拟合多项式，pk2是利用三次样条插值法的原理得到的一元拟合多项式。

结果如下：

图6：一元拟合多项式

接下来，用数字1来表示氯化镁，用数字2来表示碳酸锂，用数字3来表示碘化锂，有数字4来表示氯化铵，用数字5来表示硝酸铵，用数字6来表示碘，用数字7来表示溴化钾，用数字8来表示碳酸钾，用数字9来表示氯化钾。用拟合曲线y=x的图象来与用分段线性插值得到的拟合多项式图像及用三次样条插值得到的拟合多项式图像进行曲线拟合比较。

代码如下：

图7：曲线拟合程序

结果如下：（见图 8）。

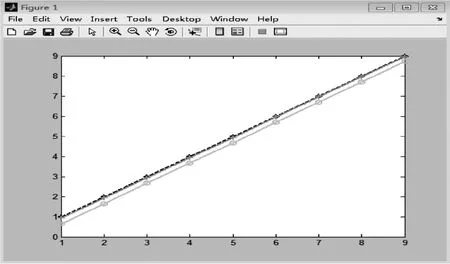
图8：曲线拟合的图像

分析：黑色线条是我们文献值的标准线条，用“*”连接的紫色线条是三次样条插值拟合多项式，用“o”连接的绿色线条就是分段线性插值拟合多项式。可以看出，紫色的曲线比绿色的曲线更加逼近我们的标准曲线，由此我们可以得到结论，三次样条插值法比分段线性插值法得到的计算值更为逼近我们的标准值，也就是说，三次样条插值法更为收敛、稳定。