科学培养学生的数学记忆能力

安徽省黄山市祁门县第一中学 洪惠敏

学生在学习过程中如果没有记忆，就不能掌握知识，更谈不上将知识应用于实践。而“死记硬背”是把记忆和理解割裂开来，降低了学生的学习效率，所以教师要转变教学观念、丰富教学手段，课堂上在传授知识的同时重视渗透科学的记忆方法。下面来探讨数学教学中如何科学培养学生的记忆能力。

一、指导学生掌握数学特有的记忆方法

1.借助图像记忆

数学是数与形的完美结合，以数助形、以形释数是数学学习中常用的方法。例如，高中数学中的函数模块，我们学习了指数函数、对数函数、幂函数、三角函数，如何记住每个函数的性质呢？其实我们只要会画函数图像，看到图像就可以说出每个函数的所有性质。又如，圆柱、圆锥、圆台的侧面积和表面积相关公式的记忆中，当头脑里浮现出侧面展开图的形状，再适当地进行推导，就可以得到公式。

2.运用口诀记忆

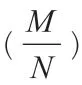
再比如，记忆三角函数的诱导公式时，我们用：奇变偶不变，符号看象限。只要记住这个口诀，我们就可以准确地记住六组诱导公式。

3.赋值记忆法

4.列表记忆法

列表记忆法是以表格的形式记忆，司马迁在《史记》的创作中就运用了该法。数学中的一些内容分开来容易记错，但是通过一张表则能够清晰地呈现出它们之间的关联。例如，我们可以利用同角三角函数的基本关系来填写特殊角的三角函数值这张表，填完表后就把特殊角的三角函数值都写出来了。

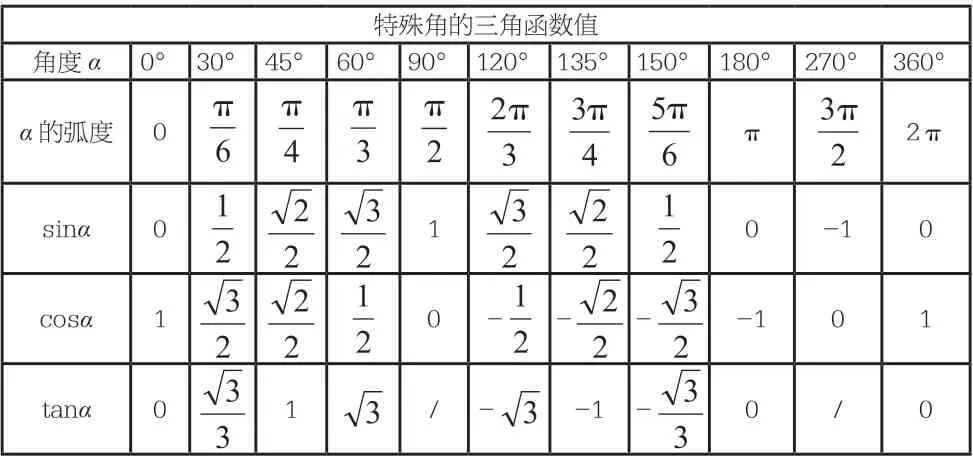
特殊角的三角函数值角度α 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°α 的弧度0 π 2π sinα 0 1 0-1 0 cosα 1 0——1 0 1 tanα 0 1/--1 -0/0

5.建立记忆网状结构图

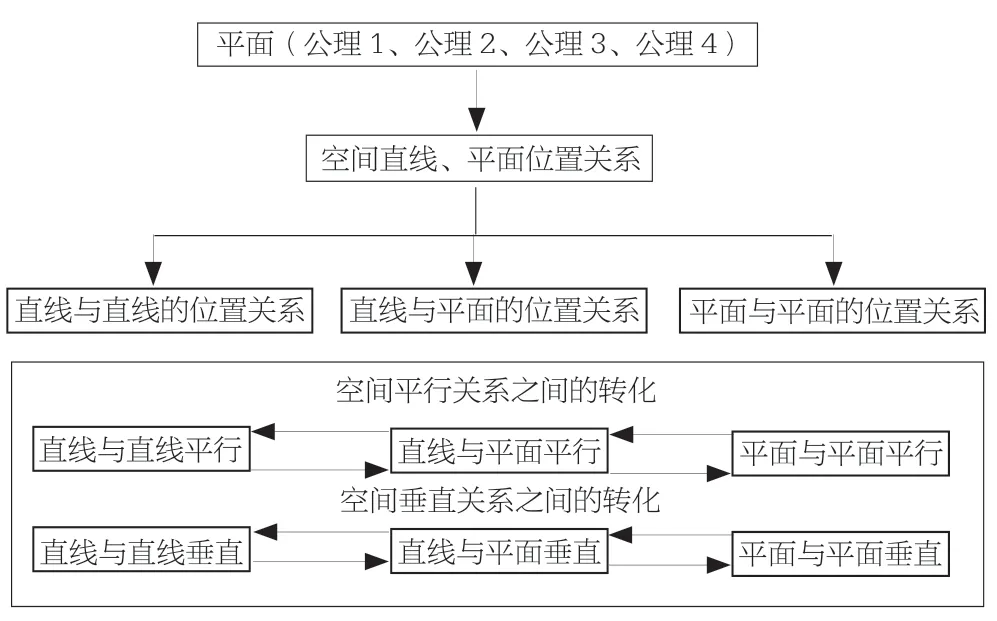
零散的、片段的记忆内容总是容易被遗忘，所以每学完一章节内容，就要把整章的内容用结构图串联到一起，再利用结构图来回忆、联想每一小块的细节。这种能力到高三显得尤为重要，因为到了高三阶段，所有知识内容都已学完，内容很多而且大部分已经遗忘，要想整体把握每一章内容，建立网状结构图是一种有效的方法。下图为点、直线、平面之间的位置关系的知识结构框架图：

二、强调有意识记能力，同时不能忽略无意识记的作用

有意识记有明确的识记目的，在识记中，学生应当高度自觉，专心听讲、开动脑筋，把注意力放在识记对象上，这样才能收到对所学对象进行理解与记忆的双重效果。

无意识记没有自觉的指向和意图，能引起人的兴趣和激发人的情绪的事物容易被无意识记。例如一场电影中比较精彩和刺激的画面或是让观者产生共鸣的情节往往很难被遗忘，这就是无意识记。在教学中，教师要丰满自己的课堂，讲课要形象、生动、有趣，能吸引学生的注意力，充分利用教具、多媒体技术、先进的理念等，使教学做到深入浅出、寓教于乐。

例如，在“直线方程”的教学中。

有意识记：倾斜角、斜率、点斜式方程、斜截式方程、两点式方程、截距式方程、一般式方程。

无意识记：在推导求和公式前，介绍数学家高斯十岁时计算当时的难题“1+2+3+…+100”，让学生从高斯的解法中掌握问题的本质。“我听见可能会忘记了，我看见可能就记住了，我做了也许就理解了。”教师应当积极运用多媒体组织课堂教学，创造条件，让学生通过数学实验进行问题探究，以丰富的教学形式呈现教学内容，提升教学效果。

三、帮助学生克服遗忘、加强记忆

1.针对遗忘规律及时复习

遗忘在学习之后立即开始，遗忘的过程并不匀速，其规律是先快后慢、先多后少。为了避免遗忘，结束知识学习后就要及时复习，可通过做习题、测试、小节复习、单元复习与总复习的方式进行知识巩固。

2.讲新课时要有意地复习和应用旧知识

通过复习旧知识引入新课或者在练习中融入旧知识等。有时在“新旧”的反复中，不仅达到了“保持”的目的，而且能加深理解。加强知识小结，构建知识框架，实现牢固记忆。

3.运用联想进行再认与回忆

学生为了接受“再认”与“回忆”的检查，除了依靠“熟记”之外，常常要靠“联想”来启发自己的“记忆”。数学永远离不开练习。要做到能“回忆”，首先要能“再认”。一般来说，顺利地进行“再认”才有可能去“回忆”。检查“再认”可以借助习题来实现。

在“幂函数”的教学设计中，学了幂函数定义，可通过下列习题巩固：

（1）判断下列函数是不是幂函数：

y=x4；y=x-2；y=1；y=2x；y=2x2；y=x3+2。

（2）幂函数y=（m+2）xm，求m=_。

“回忆”的前提是“再认”，“回忆”的启示靠“联想”，“回忆”的关键则是对问题的仔细观察，正确理解。

例题：已知a、b 都是正数，且a ≠b，下列式子中，哪些不成立，为什么？

培养学生的记忆力要使他们做到：记得“牢”；记得“快”；记得“准”；能应用。要做到这些并学好数学并不容易。数学记忆能力的培养不是孤立存在的，而是和其他能力，如观察能力、理解能力、运算能力、推理证明能力、想象能力、自学能力、抽象能力、探究能力等协调发展的，它们之间相互影响和相互促进。思维是一种非常复杂的活动，它有许多活动形式。如何在数学教学中，既向学生传授知识，又要达到培养能力、发展智力的要求，仍然是广大教师重要的研究课题。