逆向思维在初中数学解题教学中的融合

江苏省扬州市宝应县氾水镇中心初级中学 杨 娟

逆向思维是一种发散思维，指故意从正向思维的反向入手分析和研究问题。借助逆向思维解答问题能打破学生的思维定式，不仅能简化原本复杂的题目，还能缩短学生的解题时间，激活与锻炼学生的思维能力，使其在做题时能更加灵活地思考和处理问题。本文探讨了逆向思维在初中数学解题教学中的融合策略，以期能够拓宽学生的解题思路，提高其数学水平、解题效率与考试成绩。

一、从概念、定理的角度融合逆向思维

初中数学学科的知识内容涵盖广泛，涉及许多概念性知识，包括数学性质、公式、法则等。教师在讲解这些内容时要确保学生能够真正理解概念和定理的含义，夯实学生的数学基础，这样在遇到相关数学题目的时候，学生就能从概念的定义出发进行逆向思考，高效解答题目。

比如，在讲解“完全平方公式”时，教师给出了以下题目：“已知m+2n=4，那么代数式m2+4mn+4n2+2m+4n+5 的值是多少？”许多学生看到题目后会习惯性地按照正向思维分析和解答，直接用m表示n，或者用n 表示m，再将其代入要求的代数式中，但是这种做法非常麻烦，出错概率高。教师可以让学生认真观察题目，看能否有特别的发现。有学生提出题目中复杂的代数式中有的项符合完全平方公式的形式，教师先肯定他们的想法，然后继续引导：“那能否改写成完全平方公式的形式呢？怎样改写可以更加简单地求出代数式的值？”学生发现代数式中“m2+4mn+4n2”的部分可以逆用完全平方公式，写成(m+2n)2，而剩下的部分中，2m+4n 可以提出m 和n 系数的公因式2，写成2(m+2n)，而5 是常数，不用改变，所以原代数式m2+4mn+4n2+2m+4n+5=(m+2n)2+2(m+2n)+5，直接将m+2n=4 代入即可，即42+2×4+5=29。通过逆用公式，问题很容易解答。

二、从运算的角度融合逆向思维

运算是初中数学的重要教学内容，在考试中，无论是填空题、选择题，还是简答题、应用题都会涉及计算，所以教师要教会学生应用逆向思维解决运算问题。

三、从已知条件或结论角度融合逆向思维

有些数学题目的题干比较复杂，需要探讨多种情况，如果按照正向思维分析，不仅十分麻烦，还可能漏掉某种可能性，导致结果错误。所以可以从已知条件的反面入手，分析相对简单的情况，这样更容易解题。

比如，对于证明题：“请证明如果实数m、n 满足m2+n2=0，那么m=0 且n=0。”这道题的题干简单，思路也不复杂，大部分学生看到题目后的第一感觉就是题干中给出的命题是正确的，但是对于要如何证明却没有思路。这时不如从反方向思考，应用逆向思维，也就是运用反证法进行证明，假设n ≠0 且m ≠0，那么m2＞0，n2＞0，所以m2+n2＞0，与m2+n2=0 出现矛盾，故原命题正确。

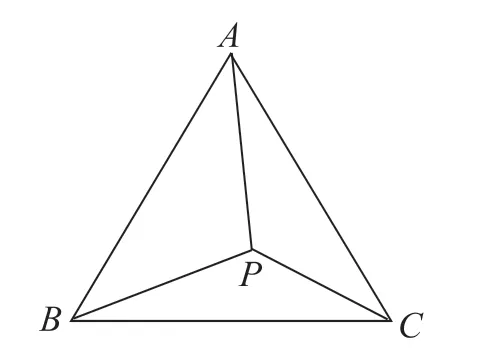
又如：“如图所示，在△ABC 中，AB=AC，∠APB ≠∠APC，求证PB ≠PC。”该题同样可以用反证法证明：先假设PB ≠PC不成立，则PB=PC，那么∠PBC=∠PCB，又因为AB=AC，所以∠ABC=∠ACB，所以∠ABP=∠ACP，由此可证△ABP 与△ACP全等，所以∠APB=∠APC，与已知条件矛盾，因而PB=PC 不成立，则PB ≠PC。

培养学生的思维能力并非朝夕之事，只有长期坚持，才能看到成效。数学作为一门抽象性、逻辑性较强的学科，对于学生而言有一定的学习难度，尤其是在遇到复杂的题目时，许多学生都不知该从何入手，容易产生畏学心理，打击学习信心。针对这种情况，教师可以在初中数学解题教学中融合逆向思维，向学生渗透应用逆向思维解题的方法和价值，提升其思维的深度和广度，让学生掌握逆向思维方法，为其今后的数学学习和发展助力。