找准活动原点，促进经验形成——以“对称和轴对称图形”教学谈“基本活动经验”形成

江苏省南京市江宁实验小学 陈 勇

2011 版新课标在课程目标上明确提出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验。”

在日常教学中，课标要求教师关注学生的“经验”的获得和发展。笔者在教学中对如何让学生获得“基本活动经验”做了一点尝试。本文就以“轴对称图形”一课为例，谈谈如何让学生获得“基本活动经验”。

“轴对称图形”一课是苏教版数学三年级上册的教学内容。教材以“蝴蝶”“天安门”和“飞机”三幅实物图片引入，让学生观察后说说它们的共同特征，得出“这些物体都是对称的”这一结论。但是，我通过对三年级之前的数学教材的研究发现，“对称”的概念过去并没有出现，只在美术课中涉及过。很显然，这里的“对称”应该源自学生的生活经验，在教学中有必要帮助学生提炼“对称”的概念。因此，我将本节课的教学内容定位为：认识对称现象和轴对称图形（做轴对称图形和画轴对称图形的另一半定为第二课时），并将课题重新界定为“对称和轴对称图形”。

一、找准生活原点，激活已有经验

在小学阶段，学生的学习应该建立在已有经验的基础之上。起始内容的学习有它的生活原点，教师应该帮助学生寻找这样的原点，促进学生的新知生长。在本节课中，第86 页的“你知道吗”恰恰就是这样一个原点，文中介绍了自然界和人工建筑之中的对称现象。为此，我将“你知道吗”作为本节课的第一个教学内容，在自主阅读中寻找、认识对称现象。

1.出示教科书第86 页下面的文字和图，让学生自学后回答：

（1）许多昆虫能在空中自由飞行，是因为它们有什么？

（2）以蝴蝶为例，它的翅膀有什么特点？（长在身体的两边，形状相同，方向相反）

教师质疑：方向相反，可不可以颠倒？

（3）在小组里说一说什么是对称现象。

2.出示教科书第86 页的图，让学生比画，说一说它们为什么是对称的。

通过以上的学习，学生形成了对“对称现象”的初步认识，即：两边形状相同，方向相反，为本节课的重点内容做了经验储备。

二、利用经验，有效探索

初步认识“轴对称图形”是本节课的学习重点。教材安排从“蝴蝶、天安门、飞机”三幅实物图中抽象出图形，通过对折、观察、交流得出“对折后能完全重合的图形是轴对称图形”。学生有了前面的经验，很容易就得出“蝴蝶、天安门、飞机”的实物的共同特点是对称的。将剪下的图形对折后，学生也会很快得出“两边完全相同”“重合”“完全重合”的结论。

1.出示教科书第83 页图（1）。观察，说一说它们的共同特征。

2.把上面的物体画下来，可以得到下面的图形（教科书第83 页图2）。

请同学们拿出剪好的图形对折，你有什么发现？

小结：对折以后能完全重合的图形是轴对称图形。

3.天安门左右对折，完全重合以后会留下一条折痕。我们把这条折痕所在的直线称为它的对称轴。

出示教科书第83 页图（3）。

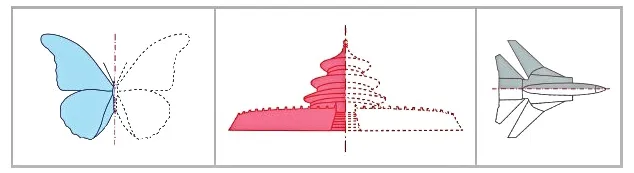
提问：你能说说飞机图和奖杯图的对称轴在哪里吗？

反思：是不是随便折一条折痕就是对称轴呢？对称轴两边的图形有什么关系？

通过教学，学生很容易将有关“对称”的经验应用到对“轴对称图形”相关知识的探索过程中，有效突破了学习难点。同时，这样的经验又会混淆“对称现象”与“轴对称图形”的关系。为此，在学习例题之后又让学生反思：图（1）中的物体能称为“轴对称图形”吗？通过反思，让学生明确：“对称”是一种现象，它可以指物体，也可以指图形，而“轴对称图形”指的是“对折以后能完全重合” 的图形。

三、合作练习，完善经验

练习是新授课必须有的环节，它对学生完善认知起到重要作用。本节课的练习更为重要，首先，练习的量比较大，其次，练习题的背后还隐藏着新的练习。因此，本课的练习采取独立练习和合作练习相结合的方式进行。

1.教科书第84 页“试一试”，让学生独立从这些图形里挑出轴对称图形。

小组讨论反思：是不是所有三角形、梯形都是轴对称图形？图中的平行四边形为什么不是轴对称图形？正五边形有好几种方法对折，都能完全重合，它为什么也是轴对称图形？

2.四人小组分工完成“想想做做”第1、2、5、6 题。在小组内汇报自己的想法。

大组交流，重点讨论：紫荆花图案，英文字母N、S、Z，中国国旗等为什么不是轴对称图形？

这样的练习安排避免了学生大量重复练习，提高了练习的效果，在不断反思中丰富了学生对“轴对称图形”的认识——轴对称图形不仅要图形的外框对折后完全重合，还要求里面的图案、颜色等也完全重合。

通过这一节课的教学，我认识到：学生的学习应该建立在学生已有经验的基础之上，教师要合理利用学生的已有经验组织教学活动，让学生充分参与，结合师生不断地反思、讨论完善认知，获得新的经验，为进一步学习打下坚实的基础。