从一道中考题探究课本例题的有效教学

苏州外国语学校 倪 波

课本例题是各地专家智慧的结晶，大部分中考题都可以在教材中找到原型，即是由课本中的例题引申、变化而来的，对初中数学课堂教学和复习回归教材、重视基础起到了良好的导向作用。本文从一道中考题入手，寻找课本的题源，从课本例题出发，通过对例题进行变式、探究、推广，达到举一反三的效果。下面将一些想法与大家分享。

一、试题呈现

（2019•安顺）如图1，半径为3 的⊙A 经过原点O 和点C（0，2），B 是y 轴左侧⊙A 优弧上的一点，则tan ∠OBC 为（ ）。

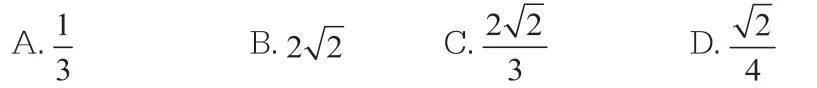
图1

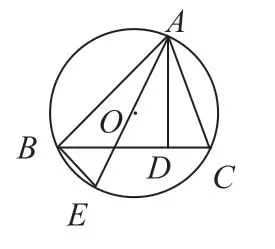
图2

二、问题分析

此中考题主要考查圆周角定理、锐角三角函数的定义，仔细分析可以看出，此题是由苏科版数学九上第121 页例3 改编而来的，源于课本，高于课本。

原题：如图2，△ABC 的顶点都在⊙O 上，AD 是△ABC 的高，AE 是⊙O 的直径，△ABE 与△ACD 相似吗？为什么？

分析： 由AE 是⊙O 的直径， 可得∠ABE=90 °， 由AD是△ABC 的高， 可得∠ADC=90 °， 再由∠C= ∠E， 可得△ABE ∽△ADC。

点评：解决课本例题的关键是利用同弧所对的圆周角相等、直径所对的圆周角为直角及相似三角形的判定方法。此题还可以做如下系列变式。

变式1：如图3，△ABC 的顶点都在⊙O 上，AD 是△ABC 的高，AE 是⊙O 的直径，AB=2.5，AC=2，AE=3，求AD 的长。

分析：可连接BE，由例题可知△ABE ∽△ADC，

图3

变式2：如图4，△ABC 的顶点都在⊙O 上，AE 是⊙O 的直径，AC=2，AE=3，求sinB 的值。

分析：

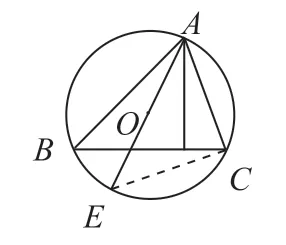
图4

图5

点评：上题解决关键是抓住直径这个条件去构造辅助线，文章开头所提的中考题与变式2 的问题本质相同，它们与课本例题本源是一样的。

变式3：如图6，△ABC 的顶点都在⊙O 上，AD 是△ABC 的高，AB=4，AC=3，AD=2，求⊙O的面积。

分析：

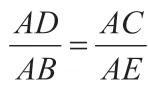
图6

图7

图8

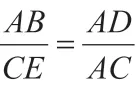
方法四：如图9，过点B 作直径BE，连接AE，具体解法请读者去思考。

点评：以上几种解题方法仍然是抓住直径这个关键条件去构造辅助线，不过在构造辅助线时可以从不同的角度入手。

变式4：已知△ABC 的顶点都在⊙O 上，AD是△ABC 的高，AB=4，AC=3，AD=2，求⊙O 的面积。

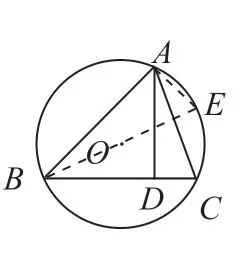
图9

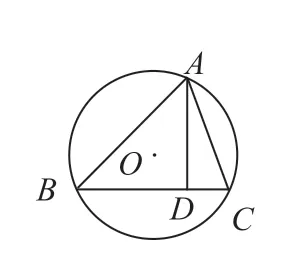
图10

图11

分析：此题没有画出相应的图形，主要考查学生的分类思想，根据题意画图时，△ABC 要分锐角三角形与钝角三角形两种情况来思考，如图10 与图11，图10 文中已经给过具体分析，图11 则可采用类似方法加以解决，如过点A 作直径AE，连接CE，具体解法由读者去思考完成。

三、教学感悟

1.以本为本

在教学中，一定要重视教材，以本为本。要认真研究教材，领会教材编写的意图，对教材内容的前后知识要理清脉络，形成体系，领会教材编写的目的，充分发挥例题的示范功能，同时让学生也重视课本，切不可舍弃课本一味刷题，否则这样往往是事倍功半的。

2.用好例题

老师要加强课本例题研究，了解例题的背景、知识能力的要求以及与相关知识的前后联系。在教学中需要对例题从多角度进行变式，要重视例题的生成，举一反三，同时还要学会去除背景，提炼出例题的数学思想与方法。

（1）将问题等化成新问题：保持原考查的知识点或能力点不变，将问题的设问方式加以变化，同时添加适当的问题背景，从而改编成新问题。

（2）将问题演化成开放性问题：保持原考查的内容不变，在改编问题的形式的同时，将新的考查点加入其中，甚至将问题开放，这样可以构造出一系列的问题。

（3）拓展问题的结论成新问题：有些数学问题的结论具有广泛性，教学时可以将这些问题的结论进行拓展，从而演变成新问题。

（4）变换条件与结论：保持原考查内容，将问题中的条件与结论进行合理变换，这样就可产生新的问题。值得注意的是，条件与结论不一定等价，因而要关注改编的科学性。

（5）条件与结论的特殊化与一般化。

3.总结提升

在以往的例题教学中，老师主要是讲解例题，然后选择同类题型变式强化，而轻视对例题的总结反思，长此以往，会导致学生在学习方法上主要是“模仿”，一旦遇到新的背景、新的问题就无法解决。教师在教学中要引导学生学会积累解题经验，学会总结反思，归纳提炼，真正提升数学思维能力。

总之，数学教学中，重视课本，用好例题，总结反思，领悟编者的意图，是学好数学和教好数学的基本前提。尤其是对课本上的例题的有效教学，更能加强对教材纲领性功能的理解，真正达到抓住课本例题、体现最佳解题示范、延拓课本例题、生长探究教育功能的效果。