IIRCT 下指数分布参数多变点的贝叶斯估计

梅梦玲， 周菊玲， 董翠玲

（新疆师范大学 数学与科学学院，乌鲁木齐 830017）

变点（change point）指的是某一位置或时刻在此前后观测值或数据遵循两个不同的模型. 变点问题是近几年统计方向研究中比较热门的话题，主要应用于质量控制、水文统计、金融经济、地震预测等领域. 目前变点分析方法主要有极大似然法、最小二乘法、贝叶斯法和非参数方法等. 关于变点问题，国内外的学者进行了深入研究，James B J［1］在1992 年对多元正态分布位置参数的变点用似然比检验做了假设检验；Kokoszka 和Leipus［2］在1998 年用累积和方法检测了ARCH 模型中的均值变点，证明了CUSUM 统计量的一致性；陈希孺［3］在1988 年研究了序列中只有一个变点的情况；1991年陈希孺［4］还在变点系列文章中介绍了基本理论及其常用的方法，如最小二乘法、局部比较法、Bayes法等，并对这些方法进行了举例说明. 近些年来，关于随机截尾试验的研究比较多，带有不完全信息随机截尾试验（random censoring test with incomplete information，简称IIRCT）由Elperin T I，Gertsbakh I B［5］首次研究，后来又有许多学者对IIRCT下寿命分布的参数估计问题进行了深入研究［6-11］. 指数分布是概率统计中一种重要的分布，关于指数变点问题的研究也有很多，胡兴［12］研究了完全数据下单参数指数族分布参数单变点的贝叶斯估计；彭秋曦［13］研究了左截断右删失数据下指数分布单变点和多变点的Bayes估计；黄月兰［14］使用了最小二乘法、极大似然法和贝叶斯法三种方法对指数分布变点问题进行研究；王黎明［15］研究了双参数指数分布的变点问题. 变点问题在实际应用中也很广泛，雷鸣等［16］、冯娜［17］、周影辉等［18］研究了不同情况下上证指数的变点问题；廖远甦［19］利用方差多变点分析技术对SARS疫情的研究；许欢［20］基于ASAMC算法对气象数据的变点进行估计. 本文主要是通过添加缺失数据，得到完全似然函数，然后基于MCMC方法研究了IIRCT下指数分布的多变点模型的参数估计问题.

1 连续型寿命IIRCT下指数的似然函数

2 指数分布的完全数据似然函数

3 多变点模型的满条件分布及Gibbs抽样

指数分布多变点模型如下：

当αi=1，βi=1时，

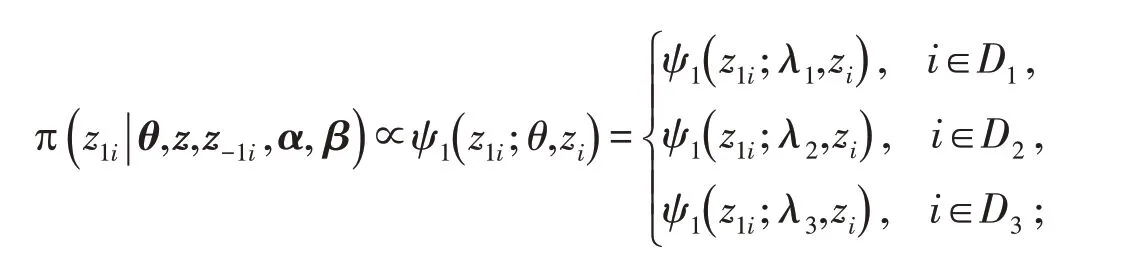
当αi=0时，

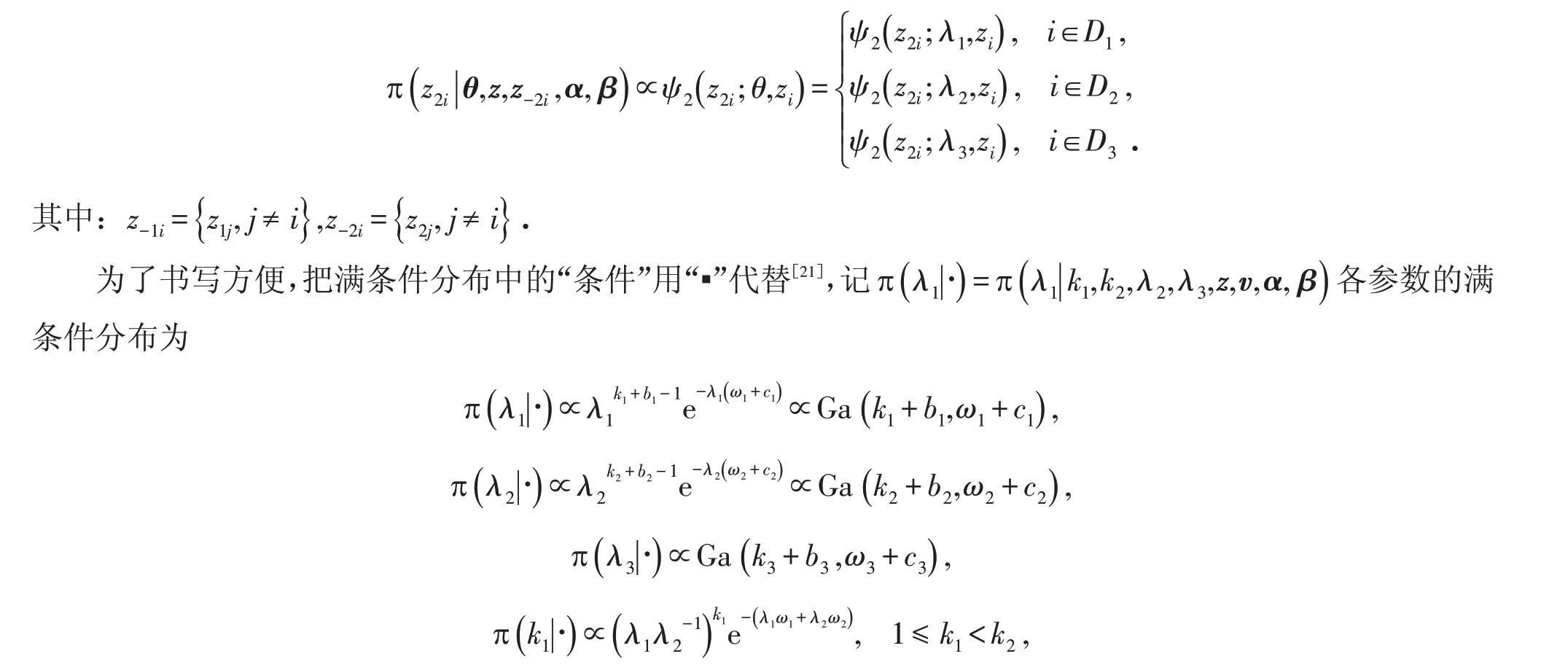
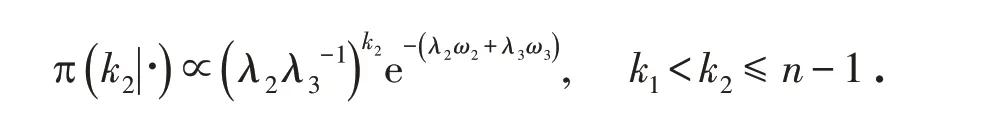
利用逆变换法可以产生z1i，利用筛选法产生z2i，由于λ1，λ2，λ3的满条件分布是伽马分布，所以这三个参数可以直接利用Gibbs抽样，而k1，k2的满条件分布比较复杂，不能直接用Gibbs抽样，所以利用Metropolis-Hastings算法进行抽样.

下面给出MCMC方法的具体步骤.

其中：m=1,2;j=1,2,3 .

4 随机模拟

令n=200，取真实值（k1，k2，λ1，λ2，λ3）=（50，150，3，8，5），取λ1，λ2，λ3的先验分布分别为gamma（6，2），gamma（8，1.2），gamma（15，2.6）. yi服从指数分布，且参数为0.5，假设显示概率a=0.8，取M=20 000，B=10 000.参数的贝叶斯估计见表1.

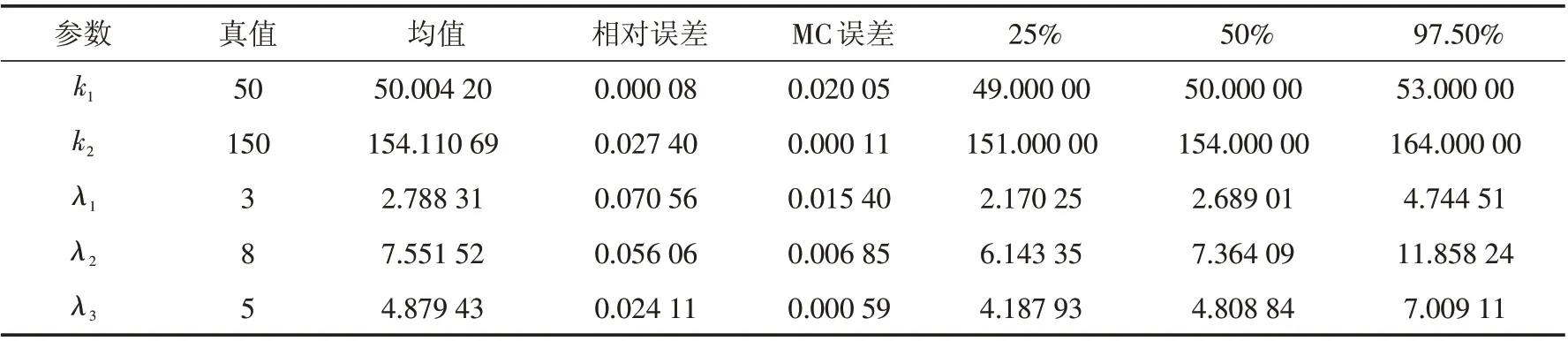
表1 参数k1,k2,λ1,λ2,λ3 的贝叶斯估计Tab.1 Bayesian estimation of parameters k1,k2,λ1,λ2,λ3

变点位置参数的Gibbs抽样迭代过程见图1和图2.

图1 参数k1 的Gibbs抽样迭代过程Fig.1 Gibbs sampling iteration process of parameter k1

图2 参数k2 的Gibbs抽样迭代过程Fig.2 Gibbs sampling iteration process of parameter k2

Gibbs 抽样收敛性判断最常用的方法是同时产生多条markov 链，MCMC 收敛性判断的常用方法是抽样时出入两组初始值产生两条链，当抽样收敛时迭代重合. 在模拟过程中，输入两组初始值分别进行10 000次迭代，k1、k2的两条迭代链如图3和图4

图3 k1 的多层迭代链轨迹Fig.3 Multiple iterative chain trajectory of k1

图4 k2 的多层迭代链轨迹Fig.4 Multiple iterative chain trajectory of k2

由表可得参数估计的相对误差不超过6%，MC误差也较小，故整体上参数估计的精度较高，Gibbs抽样迭代值波动较小，估计效果较好. 由图3和图4可以看出参数的两条迭代链都分别趋于重合，这说明由MCMC算法产生的马尔科夫链收敛.